一种多进制LDPC 码动态扩展最小和译码算法*

（陆军工程大学，江苏 南京 210007）

0 引言

1998 年，Davey 和Mackay 在有限域GF(q)上提出一类多进制LDPC（Nonbinary LDPC，NBLDPC）码[1]。相较于二进制LDPC 码，多进制LDPC 码中的非零元素全部来自于有限域GF(q)，对符号信息直接进行编译，泛化了比特级错误，具有更强的纠错能力，特别是中短码长纠错性能优异，广泛应用于需要高可靠性的通信系统。

多元和积译码算法（Q-ary Sum Product Algorithm，QSPA）是多进制LDPC 码的一种典型译码算法，基于符号间的校验约束关系，使用对数似然比作为外信息在两类节点间反复迭代以实现正确译码，译码复杂度为O(q2)。随着有限域阶数q的增加，译码中消息向量的维度增加，运算量迅速增加。为降低复杂度，Richardson 和Mackey 利用快速傅里叶变换提出FFT-QSPA[2]，旨在将校验节点更新过程中的有限域乘积运算变为简单的加减运算，算法复杂度降低到O(qlog2q)。随后，Declercq 提出扩展最小和算法[3]，将长度为q的LLR 消息向量截短为nm。由于只考虑消息向量中固定的前nm个最大值，因此进一步降低了译码复杂度。

文献[4]汇总了多种关于校验节点更新的方式，其中M-EMS 算法通过引入矩阵M和排序器S简化了选取最大值的计算过程[5]。基于检泡法产生了BC-EMS 算法，有效降低了校验节点基本步骤中排序器S的长度，提高了搜索效率[6-7]。此外，提出了许多具有良好性能、较低译码复杂度的改进EMS算法，包括T-EMS[8-9]、D-EMS 算法[10]和P-EMS算法[11]。其中，D-EMS 算法的主要思想是根据迭代次数分阶段地动态改变截短长度，以降低复杂度。

EMS 算法中，截短长度nm越小，意味着译码复杂度越小，同时也带来了较大的性能损失，是一个互相矛盾的问题。本文提出了一种动态EMS 算法，通过分析每次迭代完成后校验节点的收敛性，有选择地缩短下一次迭代时收敛性差的校验节点消息向量的长度，以降低其对译码过程产生的影响。第2 节简要介绍多进制LDPC 码的基本原理；第3节详细描述标准EMS 译码算法的具体步骤；第4节提出新的动态EMS 算法，详细描述了收敛度量值的计算方法以及校验节点更新过程中的动态截短规则；第5 节分析所提译码算法的运算复杂度；第6 节为性能仿真分析，分析对比不同条件下几种译码算法的纠错性能；最后总结全文。

1 多进制LDPC 码及EMS 译码算法原理

1.1 多进制LDPC 码

当LDPC 码校验矩阵H中的所有元素为{α-∞,α0,α1,…,αq-2}∈GF(q)(q＞2)且遵循有限域下的运算法则时，该码字称为多进值LDPC（Nonbinary Low-Density Parity-check Codes，NB-LDPC）码。当q=2 时，即二进制LDPC 码。

多进制准循环LDPC 码（Nonbinary Quasi-Cyclic LDPC，NB-QC-LDPC）的校验矩阵具有准循环特性，可以由多个循环移位矩阵分块组成。每个循环移位矩阵具有循环右移特性，降低了编译码的复杂度，同时节省了存储空间，因此在实际中获得了广泛应用。循环右移位数存储在基矩阵B中。假设一个定义在有限域GF(q)下多进制QC-LDPC 码的基矩阵B，大小为M×N，则可表示为：

式中：{α-∞,α0,α1,…,αq-2} ∈GF(q)(q＞2)；指数bm,n代表循环右移位数，规定每个循环移位矩阵中的非零值相同。因此，校验矩阵H可将基矩阵中的每个元素替换为一个p×p的循环移位矩阵得到：

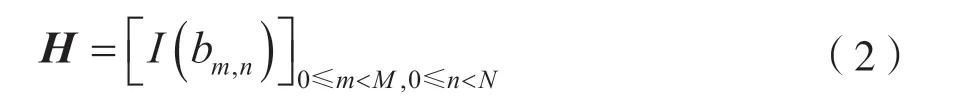
式中：当bm,n=0 时，对应单位矩阵，其中非零元素全为αbm,n；当bm,n=-∞时，对应全零矩阵；其他情况下，按照移位值循环右移，且非零元素全部为αbm,n。

一个码长为pN的符号序列c=(c0,c1,…,cN-1)与校验方程运算可以得到校验和s=(s0,s1,…,sM-1)。当s=0 时，说明序列c满足LDPC 编码规则，视为正确符号序列。

1.2 扩展最小和算法

对于多进制LDPC 码而言，每个符号位对应了q个域元素，EMS 算法更新时只利用LLR 消息向量中前面最大的nm个值及其对应域元素进行迭代，同时结合前向后向算法加快算法计算速度，但计算量也很大。

基于有限域GF(q),q=2p，假设符号序列c=(c0,c1,…,cN-1)采用BPSK 调制方式，在二进制高斯白噪声（Additive White Gaussian Noise，AWGN）信道上传输，其中第j个符号可用二进制比特序列表示，即。对接收到的符号序列z=(z0,z1,…,zN-1)进行译码时，通常利用对数似然比（Log-Likelihood Ratio，LLR），即：

由于有限域GF(q)中包括q个域元素，因此消息向量包含q个LLR 值。

下面介绍EMS 算法中的变量定义。令Uvp表示变量节点v传递给置换节点p的消息向量；表示Uvp对应的域元素向量；Vcp表示校验节点c传递给置换节点p的消息向量；表示Vcp对应的域元素向量；N(m)表示与校验节点m相连的所有校验节点；M(n)表示与变量节点n相连的所有变量节点；nm表示截短长度。译码过程中所有的运算均是有限域运算。

用Tanner 图可以很好地解释EMS 译码过程，Tanner 图中v表示一个变量节点对应校验矩阵中一列，c表示一个校验节点对应校验矩阵中一行，校验矩阵中的非零元素表示两类节点之间存在连接边并作为连接边的标签值即置换节点。通过将外信息在两类节点之间反复迭代实现正确判决，因此EMS算法的译码流程如图1 所示。

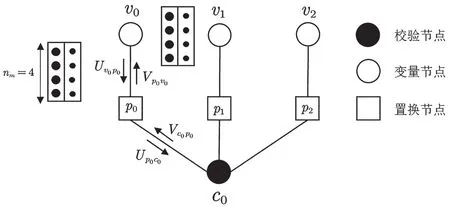
图1 EMS 算法的译码示意

EMS 算法的具体步骤如下所述。

（1）初始化。将信道初始消息Lv降序排列，并将Lv中前nm项赋值给Uvp。

（2）置换。将各项与相邻置换节点p相乘，完成对消息向量的置换。

（3）校验节点的更新过程。假设对于校验节点c而言，接收到来自相邻变量节点的消息后，利用前向后向算法完成更新。其中，对于每个运算单元，记输入消息向量分别为I和A，长度为nm，输出V，对应的域元素向量记为IQ、AQ和VQ。经过式（6）的计算，得到由校验节点到置换节点的消息向量Vcpi[k]：

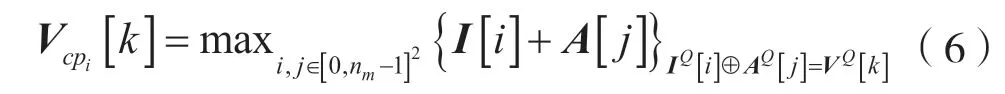
式中，i表示与该校验节点相连的第i个变量节点，⊕表示有限域运算。经过运算后得到维度为q的消息向量V。为避免不断迭代引起的数值溢出，经排序截短后进行归一化处理：

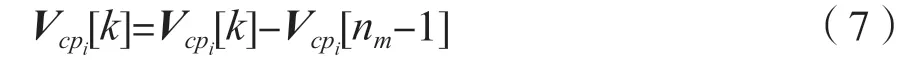
式中，i∈{0,…,dc-1}，k∈{0,…,nm-1}。

（4）逆置换。将VQcv各项与相邻置换节点p相除，完成对消息向量的逆置换。

（5）变量节点的更新过程。假设此刻变量节点为v、度为dv，则当接收到相邻所有变量节点传递过来的消息时，利用前向后向算法可以得到由变量节点v传递给校验节点c的消息向量：

式中，i表示与该变量节点相连的第i个校验节点。运算中保证在相同域元素下进行运算，随后在降序截短后进行归一化处理。

（6）判决译码。每次迭代完成需要计算消息向量Ut，将最大值对应的域元素判定为该变量节点位置的取值：

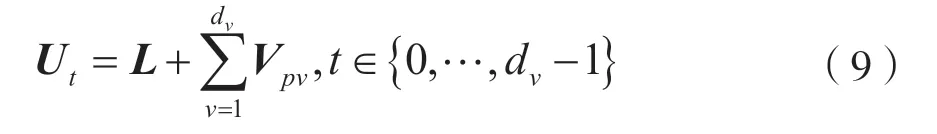
硬判决序列经式（2）计算校验和为0 时，则译码成功；否则，返回继续译码，直到达到最大迭代次数时停止迭代。

由于消息截短造成的信息缺失会降低译码的正确率，因此与QSPA 算法相比性能有所下降。在步骤（3）和步骤（5）两类节点更新过程中使用了前向后向算法（如图2 所示），其中多次调用运算单元，在此采用一种复杂度较低的算法搜索最大值。

如图2 所示，黑色方块表示一个两输入单输出的处理单元。整个校验节点的更新过程是一个并行结构，可以加快迭代的速度。处理单元的具体运算过程，如图3 所示。

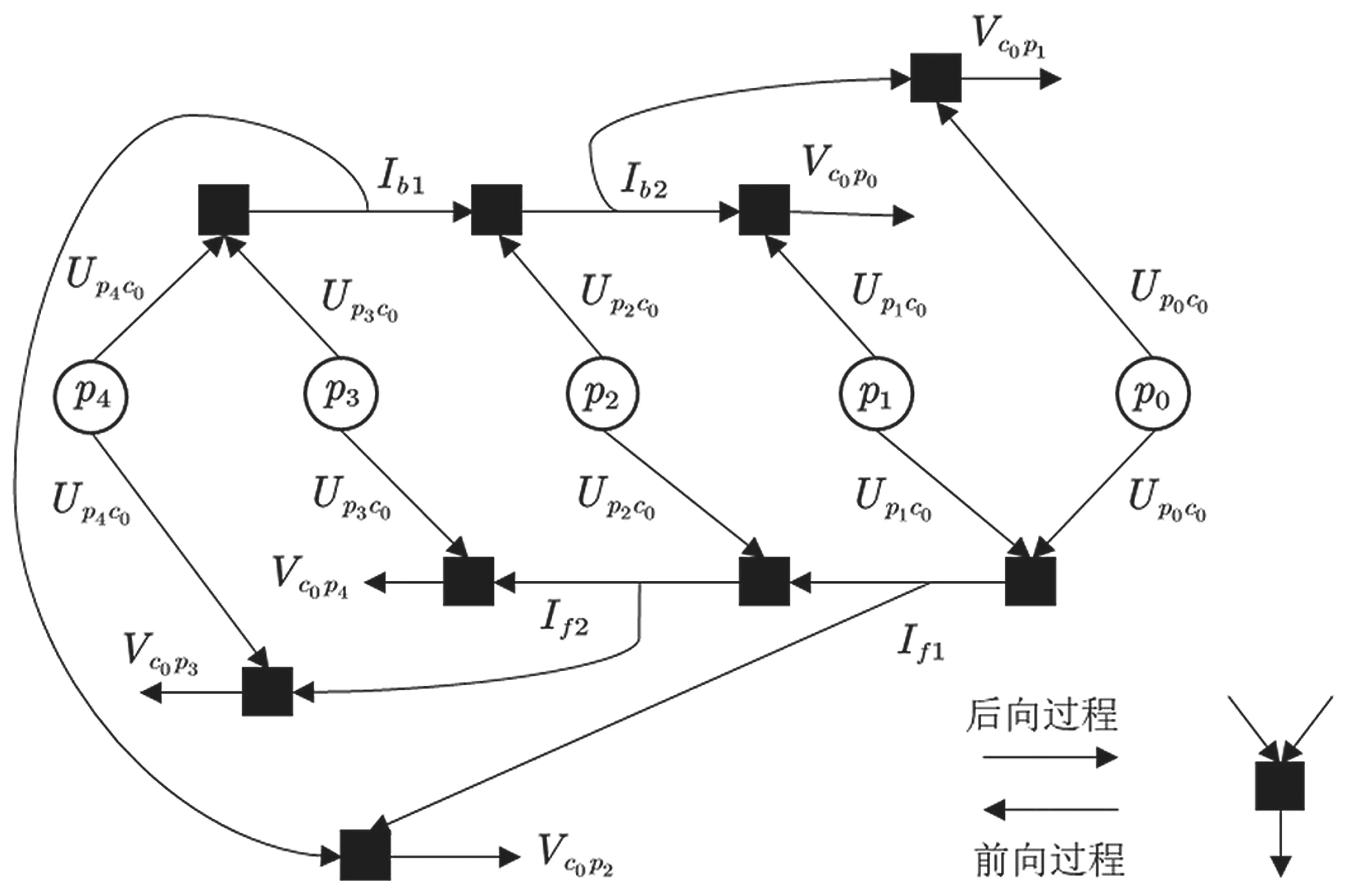
图2 前向后向过程

图3 处理单元过程

由图3 可知，每一个处理单元由矩阵M和排序器S共同作用搜索最大值。I和A是两个长度为nm的消息向量，用IQ和AQ表示对应域元素向量。用一个大小为nm×nm的矩阵M保存M[j,p]=A[j]+I[p]，用MQ保存MQ[j,p]=AQ[j]⊕IQ[p]。将一个nm的排序器S初始化为M矩阵的第一列，随后查找搜索排序器S中的最大值Smax以及对应的行，如果不属于BQ，则将Smax加入B，保存到BQ中，同时选择同一行中下一列的值替换，直到搜索得到全部nm个元素。要求输出的B要满足降序排列，BQ中所有域元素保持唯一。

2 基于校验节点收敛性的改进动态EMS 算法

在EMS 译码过程中，nm越大，消息向量信息损失越小，译码性能越好，但复杂度越高；nm越小，消息向量信息损失越大，译码复杂度降低，但译码性能损失越大。因此，需对nm进行优化，在译码复杂度和译码性能之间进行合理折衷。

对于收敛差的节点，可以适当减小截短长度，以降低它在下次迭代过程中对其他消息产生的影响；反之，不变。基于此，提出了一种新的动态EMS 算法（New Dynamic EMS，ND-EMS）。变量节点的收敛性可以利用校验和以及Vpv共同计算：

硬判决序列与校验方程在有限域下相乘得到一组校验和，当校验和s=0 时，说明译码正确，反之存在错误。式（10）结合校验和来衡量第n个变量节点收敛程度En。En为正数时，大概率不满足所有校验条件；反之，则大概率满足。对于同一个变量节点中的消息向量来说，如果最大LLR 值远大于其余值，以后可以基本维持最大值对应域元素不变，式（11）简化为消息向量中最大值与次大值之差越大[12]。在此设定一个长度为N的标记向量Tn：

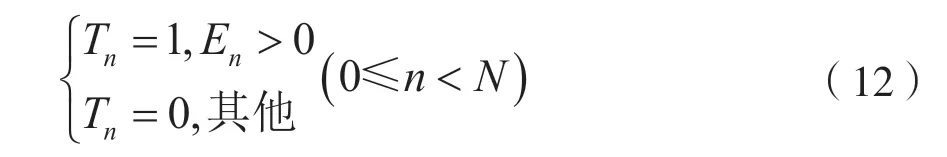
由于校验节点的更新过程是EMS 译码算法中运算复杂度较高的步骤，因此本文主要考虑校验节点的收敛性，减小其截短长度，以降低运算复杂度。一个校验节点与多个变量节点相连，因此将集合N(m)的所有变量节点可靠度量相加，则校验节点的收敛度量值为：

通常，Em是[0,dc]之间的整数，Em越大表示第m个校验方程中包含可能不收敛的符号数量越多，说明该校验节点大概率也是不准确的。因此，在下一次迭代时按式（14）改变截短长度：

式中，nm2=nm-Δ，Δ 表示减少量。校验节点m接收到的所有消息向量都做相同截短处理。下文用(nm1,nm2)表示本文算法。

因此，基于校验节点收敛性的动态EMS 算法步骤描述如下。

（1）初始化。所有变量节点初始消息向量的长度依然保持为q，暂不进行截短处理。

（2）校验节点更新。依据校验节点的收敛度量值Em计算校验节点的收敛值，见式（13），并根据式（14）对每个校验节点设置不同的截短长度，其更新过程与标准EMS 算法相同。

（3）变量节点更新。变量节点的截短长度与初始设定nm相同，不随迭代进行发生改变，其更新过程与标准EMS 算法相同。

（4）译码判决。计算消息向量Ut进行硬判决，硬判决序列利用式（2）检验。校验和为0 时，则译码成功；否则，返回继续译码，并根据式（10）利用校验和计算下一轮的En，直到达到最大迭代次数时停止迭代。

3 复杂度分析

整个校验节点更新过程中，矩阵M、排序器S以及输出消息向量B都与nm有关，搜索时间与nm成正比，因此减小截短长度一定程度上可以降低复杂度。

随着迭代的进行，消息向量中的最大值逐渐在少数几个符号之间变换。基于此，文献[10]提出了一种动态EMS 算法。最初设为nm1，当迭代次数达到Is时，截短长度由nm1变为nm2，其中nm1＜nm2，用(nm1,nm2,Is)表示，使得译码运算复杂度降低。但在较低信噪比时，受噪声的影响，每次都可能需要多次迭代才能完成译码。因此，D-EMS 算法按照迭代次数Is缩短长度可以获得更低的复杂度，但对于较高信噪比，由于噪声的影响减弱，使得迭代次数少于Is时就已经结束译码，那么截短长度可能不会发生变化，则不会降低复杂度。

设定迭代I次，D-EMS 算法的参数为(nm1,nm2,Is)，在前Is次迭代中使用nm1，后I-Is次迭代中使用nm2，用表示平均每次迭代的长度为：

本文所提改进D-EMS算法在一次译码过程中，用N1和N2分别表示校验节点采用不同的截短长度nm1和nm2的数目，则表示平均每次迭代的长度为：

表1 列举了几种算法平均在一次校验节点更新过程中的运算复杂度，不包括置换和逆置换过程，令σ=dc-2。

表1 一次校验节点更新的运算复杂度

对于FFT-QSPA 而言，进行一次长度为N的快速傅里叶变换（FFT）需要实数加法次数NlogN，乘法次数。由于完成一个校验节点的更新需要进行一次正变换和一次逆变换，因此需要乘以2。假设校验节点度为dc，输出到某一变量节点的值由除自己以外其他变量节点运算得到，因此需执行(dc-1)次FFT，每次FFT 的长度是q。此外，在正变换和逆变换之间需要进行一次乘法，实际上进行乘法q(dc-1)次，故共进行(dc-1)2qlogq+q(dc-1)次实数乘法。

在EMS 算法中，因为使用对数似然比，所以不涉及实数乘法，且在译码前已生成q×q的MQ矩阵，校验节点中只需要从中选择nm×nm即可，故不涉及有限域运算。假设校验节点度为dc，需要进行3(dc-2)次运算单元。每次需要计算LLR 值之和的M矩阵共进行次实数加法。随后搜索最大值时，搜索排序器最大值的运算量为nm-1，搜索BQ中是否重复需要nm次，因此进行2nm-1 次实数比较。

可见，一次校验节点更新的运算复杂度与截短长度成正比。所以，减小截短长度可以有效降低部分运算复杂度。

4 仿真结果

针对一个码率为0.5、码长为84 符号（504 bit）的64 进制的多进制QC-LDPC 码，利用本文所提ND-EMS 算法，设定4 种情况（32，16）、（32，24）、（16，8）和（16，12），并与文献[10]中的D-EMS对比，设定为（32，16，10）和（32，16，5）这2种情况。采用FFT-QSPA算法、EMS算法以及D-EMS算法在BPSK-AWGN 信道下进行译码，误帧率曲线如图4 所示。所有算法的最大迭代次数设定为50 次。

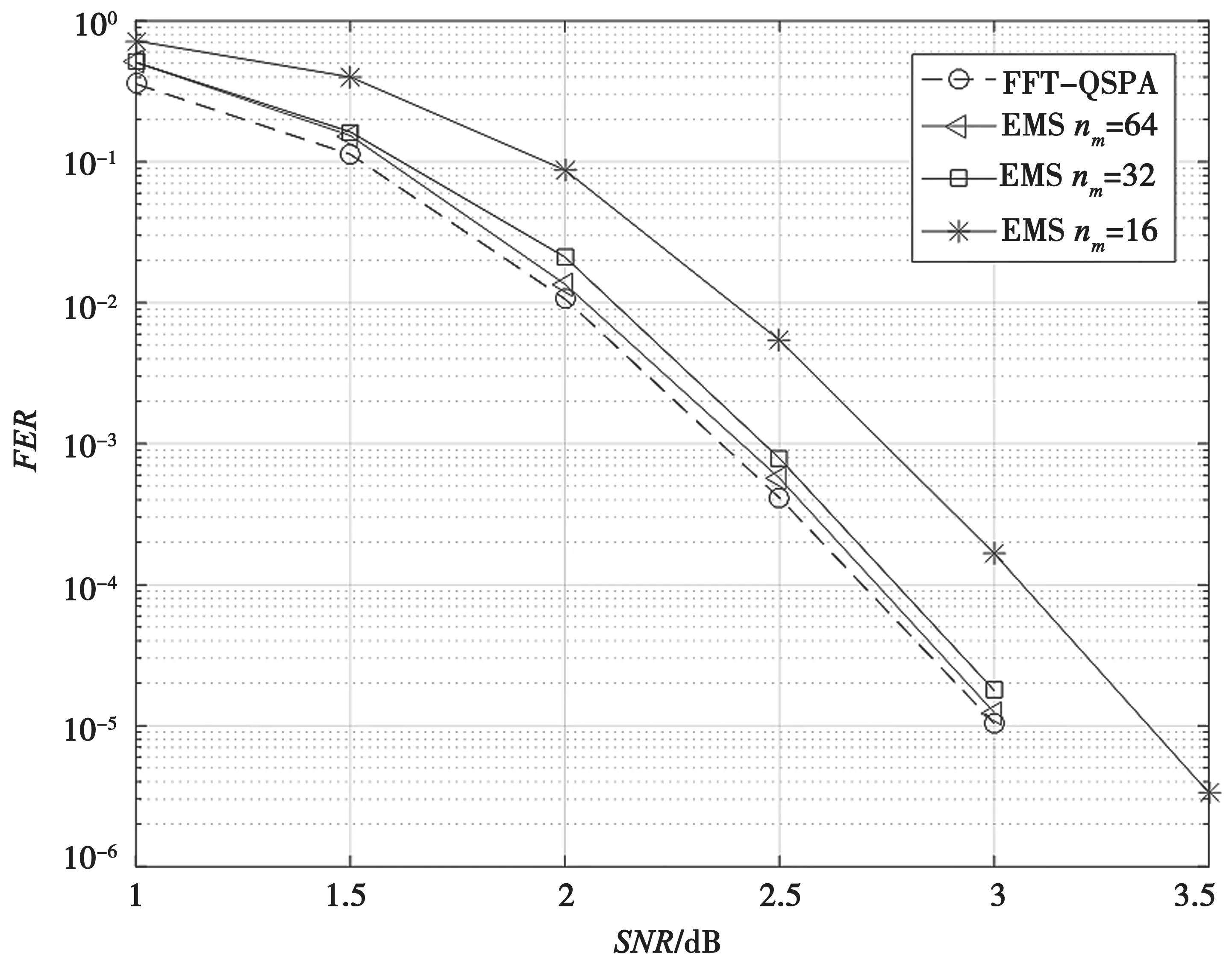
图4 EMS 算法性能与截短长度的关系

图4 中对比了截短长度为64、32 和16 时，标准EMS 算法与FFT-QSPA 的纠错性能。可知，截短长度nm与纠错性能成正比。nm越大，纠错性能逼近FFT-QSPA。在FER=10-4的条件下，nm=64 时的纠错性能与FFT-QSPA 相差小于0.1 dB；nm=32 时，相差仅有0.1 dB；nm=16 时，相差约0.4 dB。

由图5 可知，本文ND-EMS（32，16）和NDEMS（32，24）的纠错性能与标准EMS（32）相近，在FER=10-5时性能与FFT-QSPA 基本相同。NDEMS（16，8）和ND-EMS（16，12）性能逼近标准EMS（16），几乎没有损失，甚至可以达到文献[10]中D-EMS（32，16，5）的纠错性能。

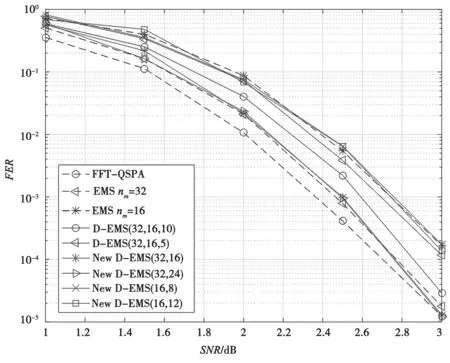
图5 性能曲线对比

相同条件下，上述4 种情况中，ND-EMS（32，16）和ND-EMS（16，8）利用更短的截短长度实现了更低的复杂度，同时不损失性能。

在一定信噪比下，记录每一帧完成译码下的迭代次数，如果无法正确译码，则记录最大迭代次数，最后平均迭代次数等于所有帧的迭代次数之和除以总帧数。从图6 可知，ND-EMS（32，24）的平均迭代次数与标准EMS 算法基本相同，ND-EMS（32，16）略高，但两者均少于文献[10]中的D-EMS 算法，并随信噪比增大差距减小，可见降低截短长度后不会增加迭代次数。同样，对于ND-EMS（16，8）和ND-EMS（16，4）情况类似。

图6 平均迭代次数对比

图7 记录每一帧使用不同长度消息向量的次数并计算nm2所占比例。比例越大，说明整个过程使用nm2的次数越多，复杂度改善的程度越大。可以明显看出，与文献[10]相比，本文的4 种方式都使用了更多长度为nm2的消息向量完成译码。

图8 记录了不同信噪比下算法的平均截短长度，可知改进算法的平均截短长度均小于标准EMS算法。对于同样设定nm2=16 条件，本文改进算法具有更低的平均截短长度，尤其在较高信噪比时，效果明显。

图7 使用nm2 的次数占总数的比例对比

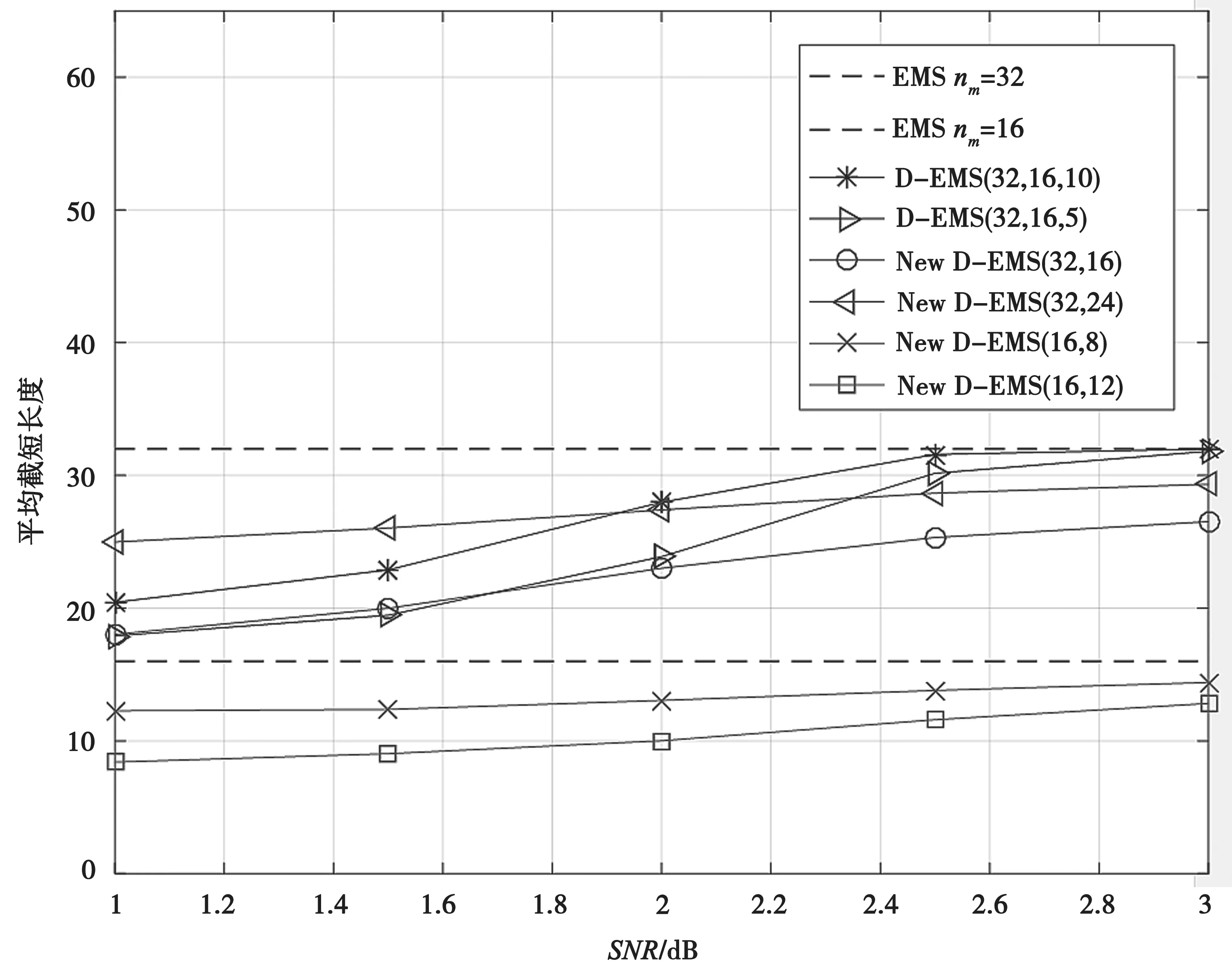
图8 平均截短长度对比

5 结语

针对EMS 算法译码复杂度较高的问题，折衷译码性能和译码复杂度之间的关系，提出了一种新的动态EMS算法，旨在用更短的消息向量完成译码。根据校验节点收敛程度不同，缩短收敛性差的校验节点，以减少其对下次迭代的影响。仿真结果表明，所提算法在使用较短消息向量进行译码时，基本不会造成性能的损失，同时具有较低的平均截短长度，降低了EMS 算法中校验节点的译码复杂度。