一道地中海地区数学奥林匹克试题推广——兼论一个条件的多余

江苏省姜堰中等专业学校 (225500) 陈 宇

证明:首先，点P,R最多只有一个在边AB,AC延长线上，且点P不与A重合.因为若重合，则∠PEA=∠B=0.不合题意.同理，R不与A重合.

若AB≤AC,由题设知∠AEC>∠ABF≥∠ACB.则边AC上必存在点R(不与C重合)，使得∠AER=∠C.

进而，点P在边AB上的位置不外乎：

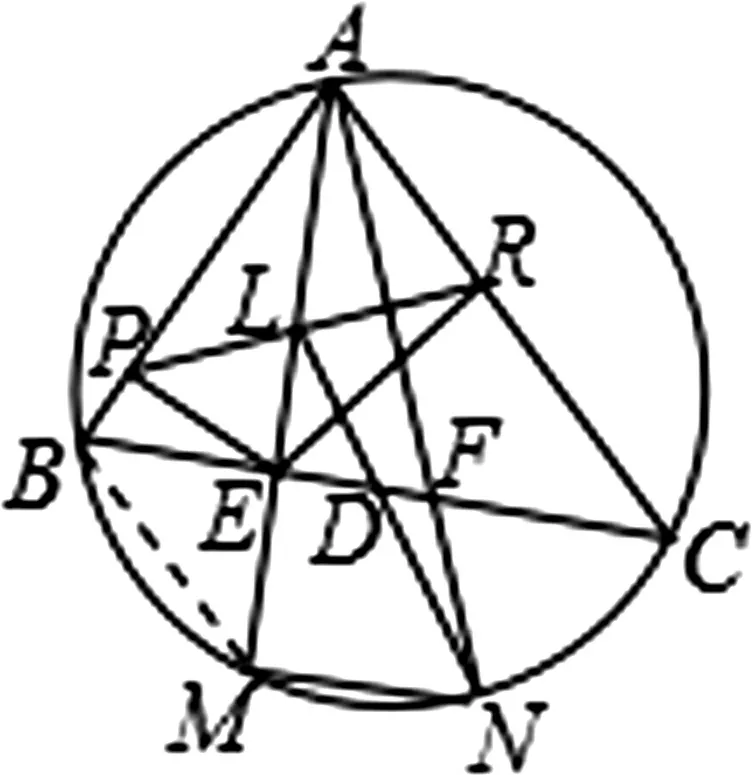
图1

图2

图3

若AB>AC，则点P在边AB上(不与A,B重合).R在边AC上的位置亦如上述点P的位置.

上述证明，只用一次四点共圆(正是这一步骤，得以让我们发现一个题设条件的多余)，然后借助三角形相似推得所需结论.其余必要过程与文[1]相同.

当点P,R分别在边AB,AC上，且满足题设条件时(如图1)，即为原赛题.