一类无理不等式的证明
2020-11-20 05:50:14合肥师范学院数学与统计学院230061万家练
中学数学研究(江西) 2020年11期
合肥师范学院数学与统计学院 (230061) 万家练 王 杰
解(证)无理不等式不易这是大家的共识.下面将利用一个简单的无理不等式来证明一类较难的无理不等式,这说明重现小命题,积累解题经验在解题中的重要.
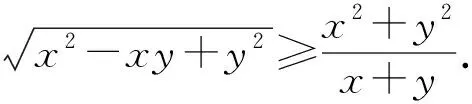
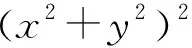
应用举例
例1 若a,b,c>0,求证
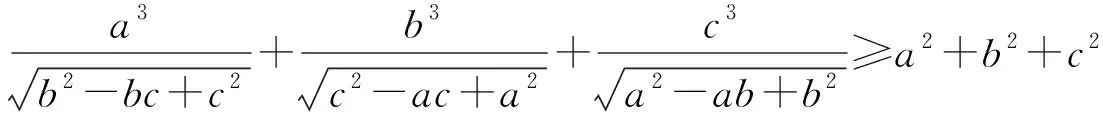

故证明①,只需证

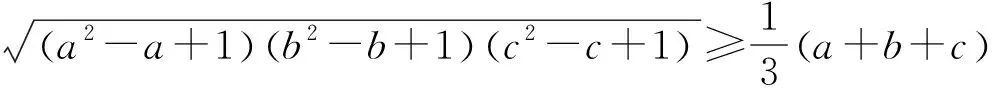
证明:由引理知,欲使②成立只需证
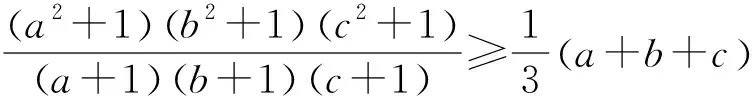
因 (a+1)(b+1)(c+1)=abc+a+b+c+ab+bc+ca+1=r+2p+1,(记abc=r,a+b+c=p,下同)
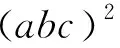
故③⟺3(r2+2p2-2rp-2p+1)≥pr+2p2+p
⟺4p2+3r2-2pr-2p+3≥0
⟺(2p-r)(p-3r)+(2p-1)(p-3)≥0.
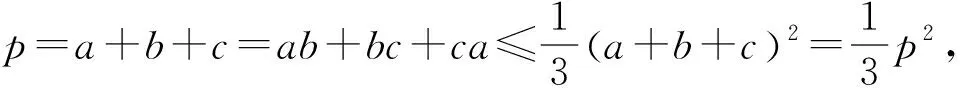
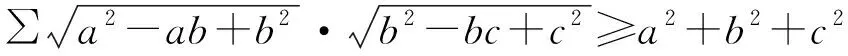

猜你喜欢
课堂内外·小学版(低年级)(2023年9期)2023-04-29 00:44:03
大众文艺(2022年21期)2022-11-16 14:49:06
疯狂英语·初中天地(2022年2期)2022-07-07 08:50:46
疯狂英语·初中版(2022年2期)2022-05-04 13:54:49
通化师范学院学报(2022年4期)2022-04-26 02:52:04
中学生数理化·高一版(2020年3期)2020-04-21 08:03:20
中等数学(2020年10期)2020-04-13 05:52:18
人大建设(2019年4期)2019-07-13 05:43:04
理科考试研究·高中(2017年7期)2017-11-04 14:06:03
发明与创新(2016年33期)2016-08-21 13:22:22

