碳纤维-钢复合结构不同粘结界面对ΔKII影响的仿真研究*

李 璐，王斌华，黄迟航

(长安大学道路施工技术与装备教育部重点实验室，陕西 西安 710064)

0 引 言

复合材料已成为与金属材料、无机非金属材料、高分子材料并列的四大材料体系之一[1]。碳纤维增强聚合物(Carbon Fiber Reinforced Polymer，CFRP)的比强度和比刚度高，加固过程不会增加钢梁自重，不对钢梁产生破坏，已经广泛应用在钢材加固补强中[2]；尤其是外贴CFRP片材的加固技术在工程加固领域中应用逐渐增多，CFRP的外部粘结可以在很大程度上延长结构疲劳寿命并减缓裂纹扩展[3-4]。

在CFRP-H型钢复合结构中，较为薄弱的环节是粘结层界面，而复合结构的力学性能与粘结层的应力状态密切相关；因此，提升复合结构的粘结层强度尤为重要[5]。由于粘结层很薄，采用传统的有限元方法易造成计算收敛困难的问题；为解决此问题，基于黏聚区的模型(cohesive zone model，CZM)模拟粘结层，被广泛应用于模拟复合材料结构的层间失效[6]。对于单一断裂模式的双悬臂梁(DCB)和端部缺口弯曲(ENF)试件中的裂纹扩展，国内外学者进行了广泛研究，邓健[7]指出当裂纹长度未超过试件半长时，由线弹性理论和小变形假设，可认为是单一模式下的断裂类型。

但不同粘结层界面对复合结构强度的增强机理尚不明确，笔者采用双线型本构模型，根据试验数据[5]对材料属性进行设置，利用Abaqus软件分别模拟了三种(刻槽/Kevlar、刻槽/Kevlar/多壁碳纳米管(MWCNT)和喷砂/MWCNT)粘结界面，建立CFRP-H型钢复合结构的有限元模型，分别施加竖直向下不同大小的位移载荷，仿真得到复合结构应力强度因子幅ΔKII与Y向位移曲线，分析得到不同粘结界面的数值结果，并与理论结果进行对比，验证数值模型的正确性。

1 本构模型及有限元模型参数设定

表1 不同试件的参数试验值[5]

图1 双线型本构关系模型

2 建立有限元模型

2.1 材料属性和模型尺寸

CFRP-H型钢复合结构，包括H型钢、粘结层和碳纤维布三种宏观结构。假定粘结界面分别与H型钢表面及CFRP粘结界面良好，在Abaqus软件中基于CZM，采用cohesive单元(响应为牵引分离)模拟粘结层，模拟多相界面内部结构的粘弹性变形；模型材料属性如表2所列，模型的几何特征尺寸如图2所示。

表2 模型的材料属性

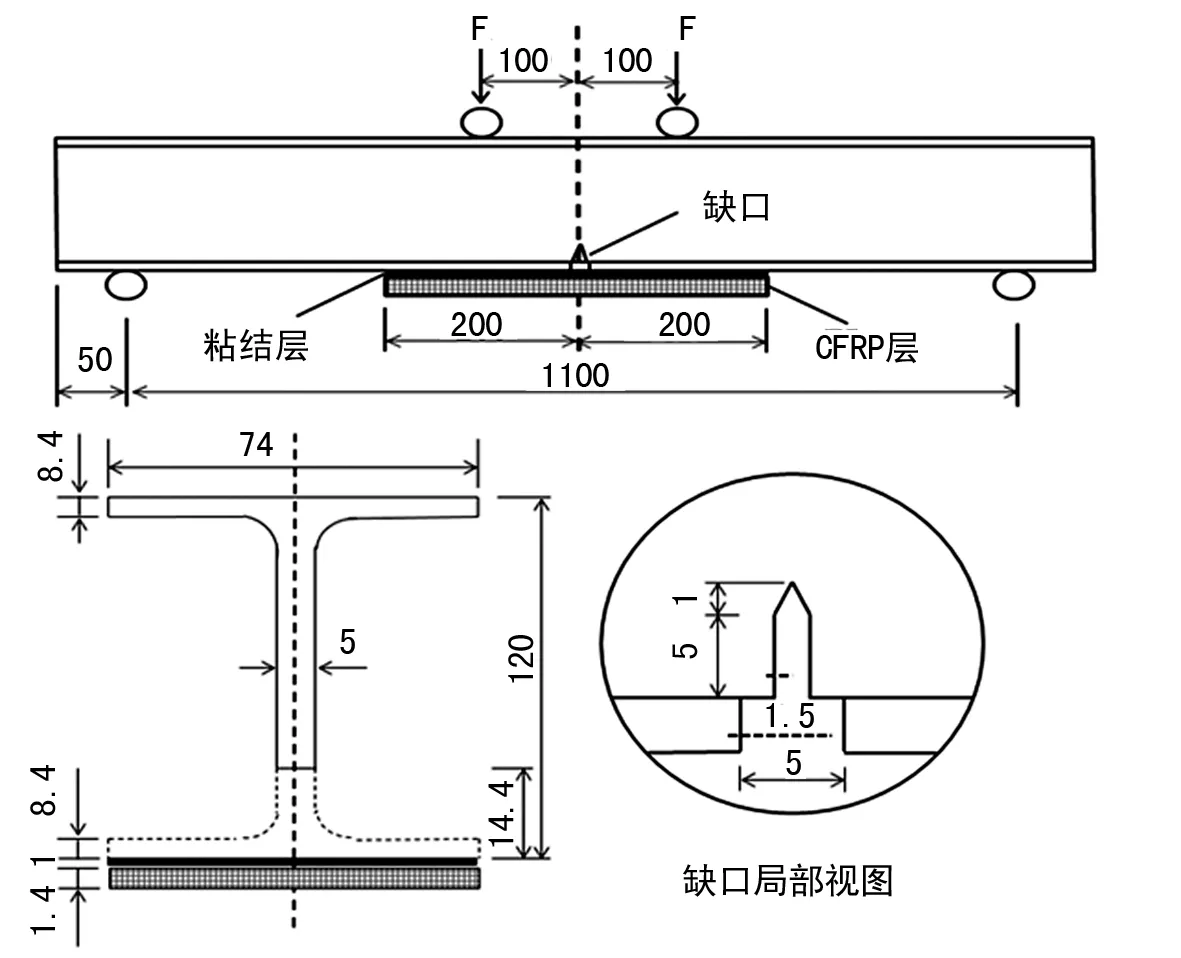
图2 有限元模型的几何特征尺寸(mm)

2.2 网格划分

在CFRP-H型钢复合结构的有限元模型中，单元共109 300个，节点159 981个。模型网格划分如图3所示：H型钢采用线性缩减积分八节点线性六面体单元(C3D8R)模拟，在其预置缺口附近采用SWEEP划分网格，且裂纹扩展方向为缺口尖端背离缺口中心；粘结层采用八节点三维粘结单元(COH3D8)模拟；碳纤维层采用C3D8R模拟。边界条件是约束支撑1的三个移动自由度、支撑2的X和Y向移动自由度，规定竖直向下为Y的正向，负载施加Y正向的均匀位移载荷；钢/粘结层和粘结层/CFRP界面使用TIE进行粘合。

图3 有限元模型的网格划分

2.3 计算结果与分析

选取粘接界面为喷砂/MWCNT的有限元模型，对粘结层的失效过程进行阐述，分析粘接界面对ΔKII的影响。规定竖直向下为Y的正向，不同Y向位移载荷的粘结层应力分布如图4所示。

如图4所示，分别对粘结层失效前见图4(a)、(b)、失效中见图4(c)、失效后见图4(d)、(e)期的法向应力(S33)和剪应力(S13)进行分析。对失效前期，从图4(a)可以看出，当位移载荷为2 mm时，载荷值为1 382 N，法向应力和剪应力集中在预置缺口附近，即位于粘结层前端18 mm的范围内，此时粘结层没有发生破坏，但粘结层前端的应力值较大，有发生破坏的趋势；由图4(b)可以看出，当位移载荷为4 mm时，载荷值为2 693 N，正向法向应力向两边移动了10 mm，负向法向应力集中在粘结层前端与CFRP接触中部位置，而法向应力值整体相较图4(a)有所减小，因为复合结构主要由剪应力承受外界施加的载荷，此时剪应力移动到粘结层后端的边缘位置，此状态下粘结层仍未出现失效。

图4 不同Y向位移载荷的粘结层应力分布(单位：MPa)

对失效中期，从图4(c)看出，当位移载荷为4.4 mm时，载荷值为2 739 N，粘结层前端第二列单元格开始退化，退化位置距粘结层前端4 mm；相较图4(b)，法向应力未发生改变，而剪应力值整体略有增加。由此可以认为粘结层的失效主要受剪应力的影响，当剪应力达到材料的极限值时，材料该部分就会退化失效。

对失效后期，从图4(d)看出，当位移载荷为5.1 mm时，载荷值为3 125 N，粘结层前端第一列单元格保留，退化方向为粘结层前端指向后端，失效长度(单侧粘结层)为6 mm，剪应力值整体略有增加，其余均未变化；从图4(e)看出，当位移载荷为6 mm时，载荷值为3 997 N，此时总失效长度(单侧)为11.9 mm，此时剪应力值达到最大，相较与图4(a)，正向剪应力值提高了1.53倍。

由以上分析可知，法向应力对粘结层的影响较小，剪应力对粘结层失效起主导作用；当剪应力达到材料的剪切强度时，材料就开始退化，从而导致复合结构的失效。MWCNT和Kevlar的增韧使得粘结层的强度提升，CFRP分担了更多的载荷，从而使得复合结构整体强度提升，ΔKII值减小。由于H型钢和粘结层接触区域受力较为集中，剪应力对粘结层有较大的影响，当剪应力达到其剪切强度时，粘结层就开始退化，裂纹扩展。仿真结果与理论结果一致，证明了模型的准确性。

对于不同的有限元模型(粘结层参数不同，其余均相同)，分别施加相同的Y向位移载荷，得到缺口附近应力强度因子幅ΔKII和Y向位移曲线，如图5所示，随着Y向位移的增加，ΔKII也逐渐增加；对于相同位移载荷作用下模型的ΔKII值，ΔKII未加固>ΔKII刻槽/Kevlar>ΔKII喷砂/MWCNT>ΔKII刻槽/Kevlar/MWCNT，表明刻槽/Kevlar/MWCNT界面增强效果最明显，可显著降低ΔKII值。

图5 应力强度因子幅ΔKII与Y向位移曲线

3 结 论

以Abaqus有限元软件为平台，采用CZM模型模拟粘结层，分别模拟了三种粘结界面(刻槽/Kevlar、刻槽/Kevlar/MWCNT和喷砂/MWCNT)，建立了CFRP-H型钢复合结构的有限元模型，施加不同的Y向位移载荷后，计算得到缺口尖端的ΔKII值，仿真结果与理论结果吻合较好，得出以下结论：

(1) 对于CFRP-钢复合结构模型，各粘结界面应力值变化范围较小，说明粘结层内部产生相互作用的内力越小，CFRP承担了更多的载荷。

(2) 在粘结层中加入MWCNT和Kevlar可以显著提高粘结层的剪切强度，有效降低缺口处ΔKII值。由实际情况可知：Kevlar短纤维的自由端可以随机嵌入到金属表面的槽中和CFRP布表面缝隙中，增强复合结构强度。

(3) 该模型模拟的CFRP层数和粘结层厚度为定值，为得到最优的CFRP层数和粘结层厚度，仍需深入研究。