面向工业混杂系统故障检测的扩展数据逻辑分析方法

孙中建，杨博，齐楚，李宏光

（北京化工大学信息科学与技术学院，北京100029）

引 言

对于连续工业过程中的某些生产系统，一些离散过程参数如电机、阀门和开关等也会经常发生状态改变，因而对生产系统的安全性和稳定性产生影响[1]，即体现了混杂系统特性。混杂系统是指同时包含离散事件系统和连续变量动态系统、两者又相互作用的系统[2]，其特点是随时间连续变化的同时，也受到离散事件的驱动。故障检测技术已被证明能够提高生产过程的安全性并降低制造成本[3]，其中广泛应用的技术可分为基于模型、基于知识和基于数据驱动的方法[4]。因不需要精确数学模型和大量先验知识，近年来基于数据驱动的故障检测引起广泛研究[5-8]，而对于工业过程中的混杂系统的故障检测相对关注较少[9-10]。

采用知识分类技术构建工业过程数据监测模型，可以为工业过程混杂系统的故障检测提供新方法。而在故障检测分类方法中，模型的可解释性引起了研究人员的关注[11]，进而通过发现可解释模式的知识来分析和检测故障[12]。数据逻辑分析（logical analysis of data, LAD）是一种描述性机器学习方法，通过分析历史数据中变量的组合来描述不同的分类。与一般的数据驱动的故障诊断方法相比，优势在于其强大的解释能力，能够在历史数据中挖掘隐藏的相关联的物理现象，并且根据专家知识进行因果关系的表达，使其在工程、金融、医疗保健等多个领域得到了广泛的应用[13-15]。在工业领域，使用LAD 方法检测和预测物理现象，同时解释现象背后的原理，Mortada 等[16]将LAD 用于检测和隔离航空公司机队的劣质涡轮压缩机，通过监视某些性能指标和专家系统的知识，发现了劣质组件独有的模式。Shaban等[17]提出了一种适用于复合材料碳纤维增强聚合物布线工艺的过程控制技术，通过监视某些加工特征和参数来检测特征模式，并使用它们在特定范围内控制加工零件的质量。Jocelyn等[18]将LAD 应用于职业健康和安全领域，尤其是表征了与机械相关的不同类型的事故，并将其与故障的根本原因相关联，生成了用作确定风险因素和潜在事故原因的优先级的模式，以帮助安全从业人员做出有关机器安全措施的决策。Ragab 等[19]将LAD 应用于诊断复杂工业化学过程中的故障并解释这些故障的潜在原因，并与其他常见的机器学习技术获得的结果进行比较，结果表明LAD 的性能与最精确的技术相媲美。

LAD 基于离散化的历史数据进行模式提取，适用于针对混杂变量的过程监测，但LAD 在挖掘规则过程中由于对连续变量离散化表示而严重丢失了连续变量的趋势变化信息，而过程数据的动态特性中包含的潜在信息需要纳入模型[20]，否则难以挖掘到令人满意的结果。另外，LAD 在提取特征时忽视了变量的权重差距，容易获得无法体现过程特征的冗余规则，因此，本文提出一种面向工业过程混杂系统故障检测的扩展数据逻辑分析（extended logical analysis of data,ELAD）方法，挖掘混杂系统过程数据中的隐含规则及连续变量的变化趋势，删除冗余规则，获得丰富的故障信息和高效的故障检测模型，应用于工业煤气化汽包过程实例，以验证其效果。

1 数据逻辑分析

数据逻辑分析能够发现历史数据中隐含的知识，相关研究证明了发现知识的有效性[21-22]。LAD迭代提取能够表征不同类别的模式，直到所提取模式能够完全表征所有的观测值，因此提取模式中存在的冗余模式引起进一步的研究[23]。

作为有监督的分类学习算法，LAD 基于优化领域和布尔函数理论，对多类问题进行模式提取[24-26]。其最大的优势在于强大的解释能力，根据从训练数据集中提取的可解释的模式构建决策模型。LAD主要包括数据二值化、模式提取和理论形成三个步骤[27]。二值化处理按升序对变量Z 的观测值进行如下排序：

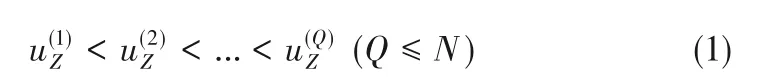
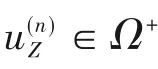
二进制属性bZ,i(i=1,…,r)由基于切点αZ,i的数值变量Z形成，即：

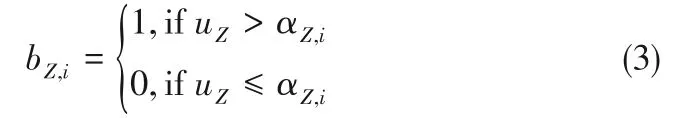
正负模式的生成是相对称的，为了简便起见在此仅描述正模式的产生过程。模式生成最直接的方法即为枚举产生，所产生模式需至少包含一组正观测值并且不包含任何负观测值。本文基于LADWEKA 平台采用启发式方法提取模式[28]，提取的模式有两种形式：自变量和组合变量。自变量由自身规则即直接影响系统的分类结果，无须检测其他的变量，可以根据自变量的变化范围给出结果产生的原因。组合变量是通过不同变量之间分别满足不同的条件而组成的规则，可以获得难以发现的变量之间的联系，通过共同作用影响模型。其算法描述见表1。

表1 LAD算法描述Table 1 Logical analysis of data algorithms

2 扩展数据逻辑分析

2.1 ELAD框架

LAD 能够生成表征特定观测值的不同规则，但由于工业过程中存在众多高维、复杂数据组，直接使用所有数据将导致模型训练速度慢且包含大量冗余信息，这里，提出一种扩展数据逻辑分析（ELAD）方法，在建立ELAD 模型时需要首先对原始数据进行降维[29]，但同时为了保留表征原始数据特性的过程变量，在不改变原始数据结构的情况下，选择使用灰色关联分析对数据进行处理，排除对过程无影响变量的信息，指导选择过程以解决选择问题[30-31]。ELAD 产生的规则必须经过进一步的筛选才能构成模型，因此模型构建时通过与关键变量的灰色关联度对相关变量的优先度进行选择，从而解决规则冗余的问题。在确定单元窗口参数后，引入动态标准差及趋势变化量，丰富变化信息以避免信息丢失。

ELAD 能够自动选择相关性强的变量，并在不需要人为干预的情况下进行模式提取，删除冗余规则并形成具有可解释性的分类模型，主要包括灰色关联分析、挖掘波动趋势、挖掘规则、模式选择与模型构建四个步骤。模型建立的流程如图1所示。

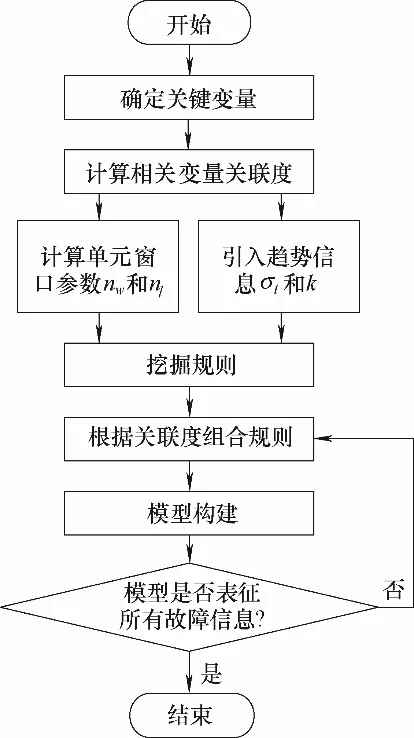
图1 ELAD流程图Fig.1 The flow chart of ELAD

2.2 灰色关联分析

灰色关联分析是一种根据因素间发展趋势的相似程度以衡量因素间的关联程度的方法[32]，因其可以直接评估原始数据，受到广泛关注并在工业领域成功应用[33]，本文选用灰色关联分析法以实现相关变量的选择并用于后续步骤的规则提取，能够初步避免冗余规则的产生。

为了消除量纲对于计算结果的影响，在关联分析之前对所有变量进行归一化处理。设表示关键变量的参考序列为x0={x0(k)|k = 1,2,…,m }，表示相关变量的数据组存在 n 个变量 xi={xi(k)|k = 1,2,…,m }，i=1,2,…,n。因此x0(k)与xi(k)关于第k个指标的关联系数ξi(k)有：

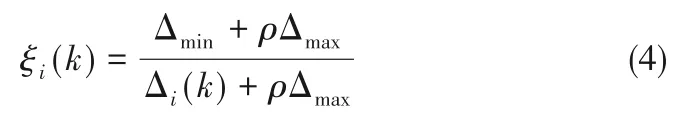
其中，i=1,2,…,n;k=1,2,…,m。

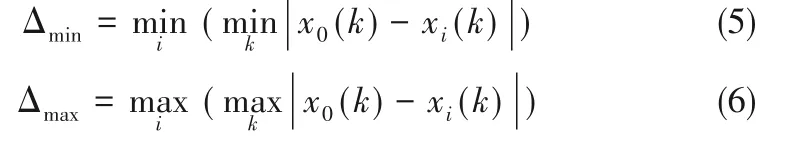
分辨系数取值区间为[0,1]，取值越大则分辨率越大。第k个指标与参考序列的关联度为：

2.3 挖掘波动趋势

为了挖掘变量的变化情况尤其是过程中的波动信息，受到基于均值和数据分布的形态特征改进符号聚合近似方法的启发[34]，在模型中引入基于历史数据的标准差以表征变量的持续波动变化情况，标准差能反映数据集离散程度的同时不受样本个数的影响，相比较于均值或其他特征变量，波动变化情况在过程中将更清晰地反映运行状态的改变。

设变量可表示为x ={x(k)|k = 1,2,…,N }，那么标准差σ为：

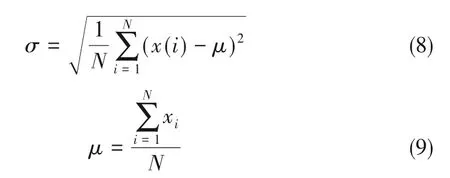
由式（8）、式(9）计算的标准差反应变量x 的离散程度，而针对于过程变量需要考虑的是不同状态时的变化情况，因此本文提出单元窗口波动趋势的概念。单元窗口[35]是指在一个观测周期内，所包含的所有时间序列数据集，在单元窗口内部对应的不同变量存在着不同的趋势特征，因此同一个单元窗口内存在多个标准差，换句话说，对于变量而言在该窗口内只有一个趋势特征值，即计算所得标准差能够体现该变量最新的发展情况。

单元窗口宽度nw太大不仅对历史数据的要求过高，而且无法体现变量最新的波动情况，宽度太小也会造成计算精度缺失，甚至在波动的工业数据中失去意义。在确定单元窗口宽度并计算标准差后，需要选取适当的窗口滑动长度nl，窗口滑动长度决定趋势波动的变化精度，当长度越小时将获得频率越高的对比结果，如图2所示。

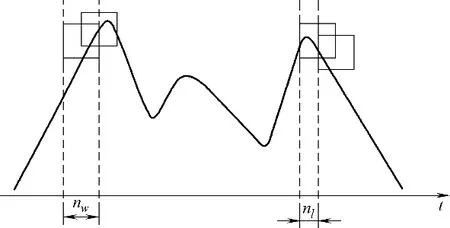
图2 单元窗口及滑动长度Fig.2 The unit window and slide length

为了获取相同的单位时间段内的变化信息，采用固定的单元窗口宽度nw(nw≪N)，nw需要根据变量进行适应性调整，为了能够获取迅速变化时的信息，单元窗口宽度选取为窗口内平均值变化为该变量波动值的时间长度，不超过该变量极值至均值的时间长度，可得到动态标准差σt为：

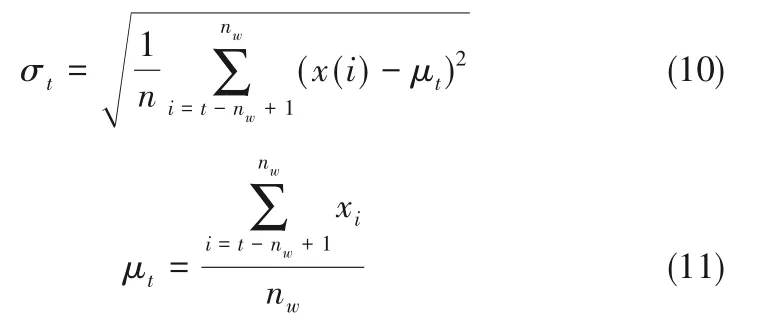
为了能够提取灵敏的波动趋势特征，采用窗口滑动长度nl=1 进行后续分析[36]。在确定单元窗口参数后，为关键变量引入趋势变化量k={+1,-1}，k=1时表示关键变量当前时刻较上一时刻增加，反之为降低。引入该值能够增强模型表达能力，进一步丰富故障的特征信息。

2.4 模式选择与模型构建

ELAD 参照灰色关联度选择相关变量进而提取模式，在表征所有的观测值的同时选用关键变量进行表达，相比于单纯基于统计的传统方法，能够增强模型的准确性和有效性。假设某过程有关键变量A，经过灰色关联分析后筛选出2 个相关变量C、E，可行方案将从以上3个变量及其波动参数依次为B、D、F 的模式组合中产生。每个可行方案都将按照覆盖率和重叠率进行组合，覆盖率指的是该模式能够表征的观测值的数目，重叠率指的是所有观测值中被多个模式覆盖的数目。覆盖率能够体现该模式的表征效率，重叠率则体现模式中存在的冗余观测值。最终形成的可行方案将在优先提取关键变量的模式后，选取覆盖率高且重叠率低的模式进行组合，产生的模型可能包含不同的可行方案。

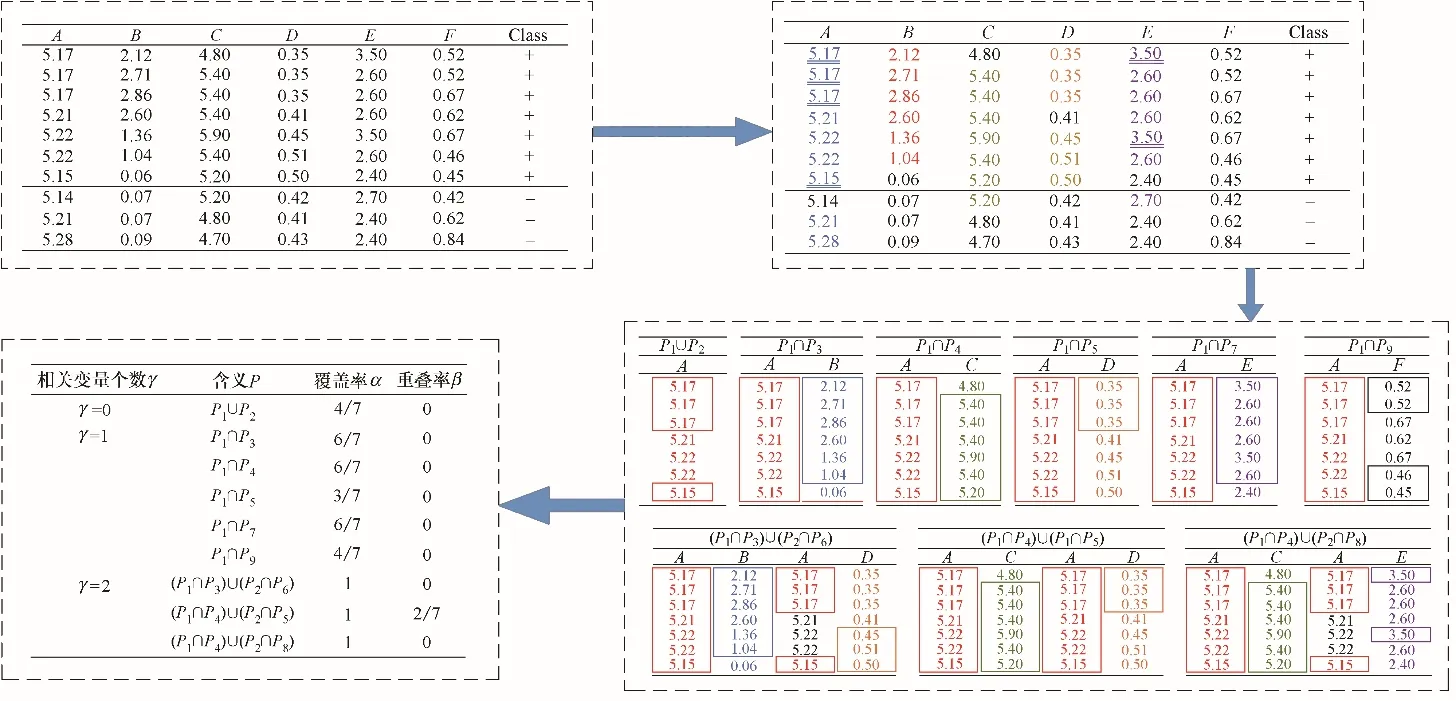
图3 模式选择过程Fig.3 Patterns in selecting

图3展示了模式选择的全过程，由灰色关联度、覆盖率、重叠率共同选择出可行方案。在所有变量中，发现了不同的9 种基本事件，其中与关键变量A相关的基本事件有2种。首先计算关键变量基本事件的覆盖率均不为1，因此选取相关变量的模式进行组合，对每个组合模式的覆盖率和重叠率进行计算，直至获得覆盖率为1 的模型才足以表征所有的观测值，在最终获得的可行方案中选取重叠率最低的作为检测模型。根据上述方法能够获得P((P1∩P3)∪(P2∩P6))和P((P1∩P4)∪(P2∩P8))两种可行的模型。

2.5 模型的概率计算

模型由多个可行方案即模式组成，每个模式由1 个或多个规则组成，每条规则可能包含多个事件的合并集关系，每个事件的发生概率使用符合该事件的观测值与所有的观测值之比表示：

若规则Mi中含有多条规则相交的情况，根据贝叶斯定理[37]有：

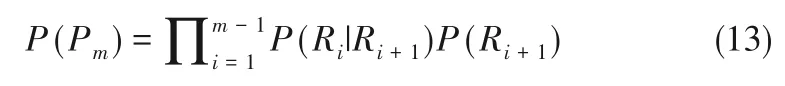
针对不同的可行方案，由组合模式的有限个事件P1,P2,…,Pn并集计算可行方案的概率，根据庞加莱公式[38]有：

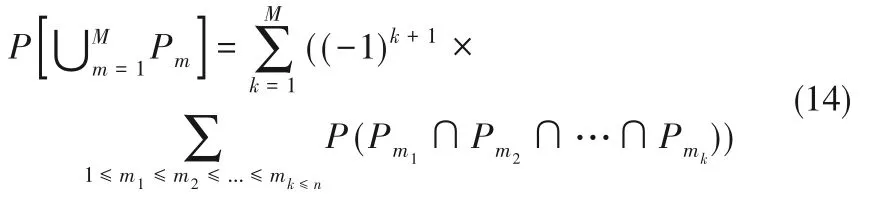
最后，分类事件的可行解概率由所有可行方案Sq(q = 1,2,…,Q)计算：

3 故障检测实例

3.1 工业煤气化系统

考虑某工业煤气化合成气洗涤单元中压汽包过程，其工艺流程如图4 所示。氧气经由氧气缓冲罐进入预热器，中压循环水使其温度加热到指定温度，混合蒸汽后输送至气体混合器。中压饱和蒸汽被蒸汽电加热器加热至指定温度与氧气按比例混合，与粉煤一同输送至气化炉。中压汽包液位控制给水流量大小，是中压汽包过程监测的关键参数。根据工艺知识和数据分析，共有12 个与该反应过程相关的变量，其中包含1 个离散变量，如表2 所示。通过对汽包液位变化机理的研究，汽包故障有两种常见情况，即液位过高或液位过低，液位的变化不仅取决于通过阀门控制的流量变化，同时也受到循环过程中环境参数连续变化的影响，因此在过程中同时关注阀门的操作以及监测变量的状态。

3.2 选取变量与规则提取

确定中压汽包液位为关键变量以后，选取灰色关联算法分析液位与其他连续变量的相关度，图5描述了过程变量间的灰色关联度。

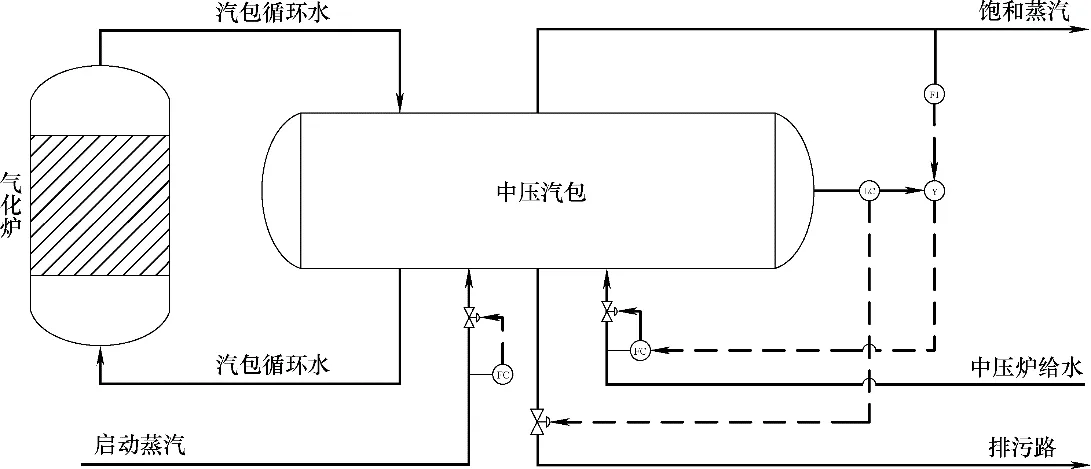
图4 汽包过程工艺图Fig.4 The steam drum process diagram

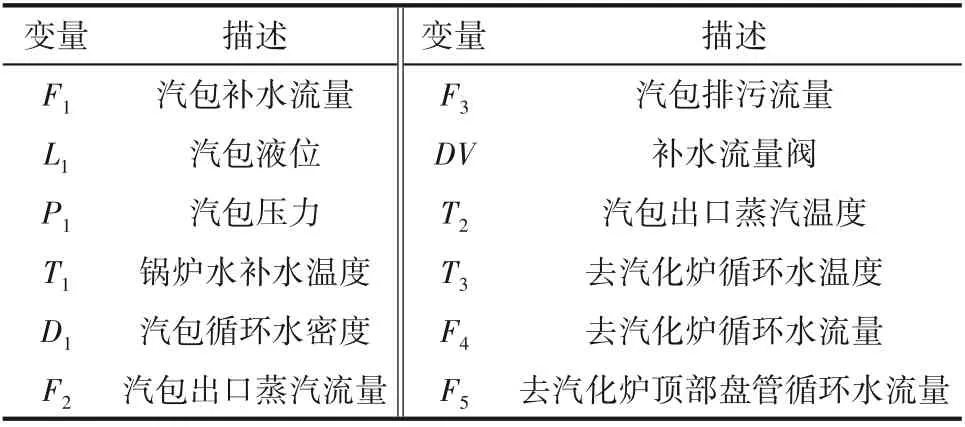
表2 相关变量及其描述Table 2 Correlated variables and its description

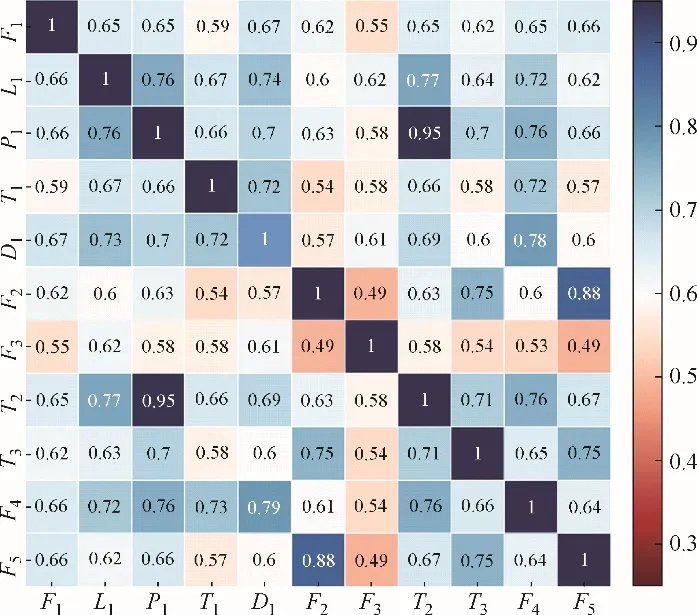
图5 变量间的灰色关联度Fig.5 The grey association analysis between variables

可以看出液位和其他连续变量的相关程度，采用试错法选取阈值为0.65，得到与液位相关程度高的6个变量分别是补水流量、汽包压力、锅炉水补水温度、汽包出口蒸汽温度、汽包循环水密度和去汽化炉循环水流量，因此选用以上7 个变量以及离散变量组成的数据集进行后续的分析。表3给出了相关过程变量部分数据，图6为数据集的可视化结果，红色表示故障，蓝色表示正常，使用以下算法不能准确识别故障同时改变了原始数据的结构，无法获取能够表征特性的规则信息。

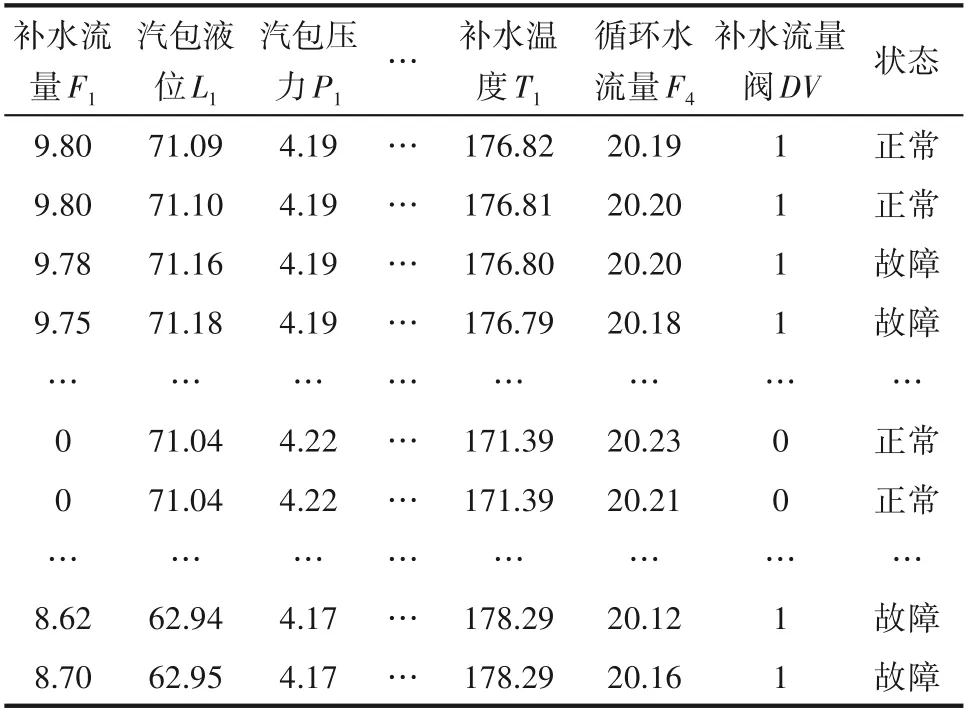
表3 相关过程变量数据Table 3 Correlated variable data

3.3 生成检测模式

表4 为提取由8 个变量组成的数据集，利用ELAD 算法进行隐含模式的挖掘。为了能够体现变量的变化情况，在数据集中添加基于历史数据的变量标准差信息。在众多的规则中设置覆盖阈值为2%，这意味着仅包含少量数据的规则将被过滤，保留适用于多组数据的不同规则的组合。

训练过程如下：

（1）根据液位变化计算单元窗口参数取nw=30，nl=1，并计算k；（2）提取隐含规则，正常数据不能包含在规则内的同时必须有一条以上的故障数据被规则所描述；（3）规则选择与组合，根据覆盖阈值选取含有关键变量的规则计入模式，对于未能包含的故障信息使用相关变量进行表示。

经过训练，共建立四类故障检测模式，分别是：

检测故障模式M1，由两条规则组成，M1=R(1)∪R(2)；

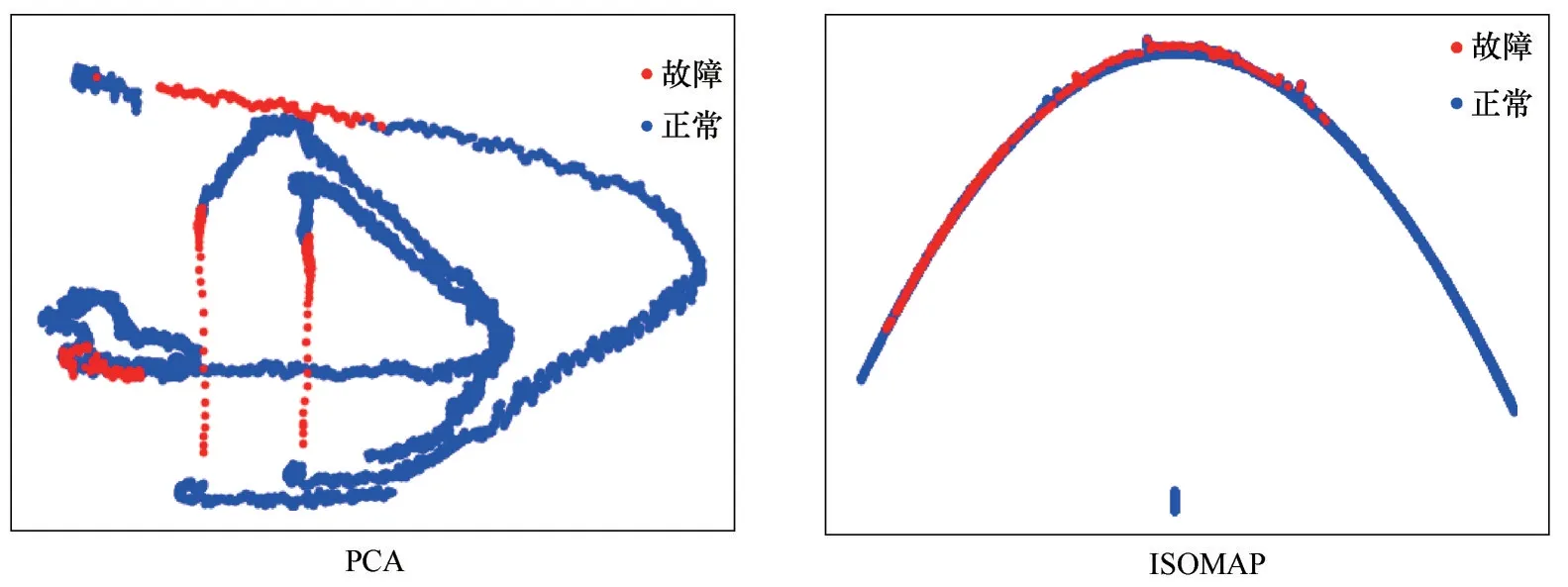
图6 数据集可视化结果Fig.6 Visualizations of the dataset

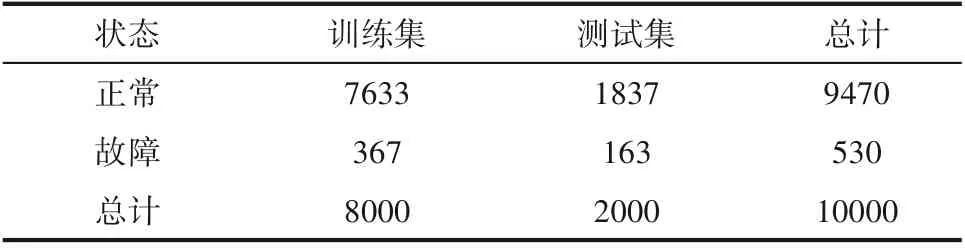
表4 训练集和测试集的数据总数Table 4 Number of training and testing datasets

检测故障模式M2，由两条规则组成，M2=R(3)∪R(4)；

检测故障模式M3，由两条规则组成，M3=R(5)∪R(6)；

检测故障模式M4，由两条规则组成，M4=R(7)∪R(8)。

其中，M1和M2表示液位过高的故障，M3和M4表示液位过低的故障。构成四种检测故障模式的基本事件的含义和不同规则在故障数据中的覆盖率如表5和表6所示。

以上检测模式可解释如下：在检测模式M1中，补水流量阀为开，液位呈上升趋势，液位高于71.105并且液位变化波动较大为故障，表达式中出现离散变量意味着在该情况下补水流量阀值与正常状态时相反；或者当满足液位高于71.105，流量大于3.423，流量波动较小且循环水密度波动较小时为故障。在检测模式M2中，当满足补水流量阀开，液位呈上升趋势，液位高于71.105 同时补水流量大于3.1788时为故障；或者当满足补水流量阀开，液位呈上升趋势，液位波动较大同时补水流量波动较大时为故障。检测模式M1和M2等价，均为液位过高时的可行方案，M3和M4为液位过低时的两种可行方案，表7为计算的故障发生概率。

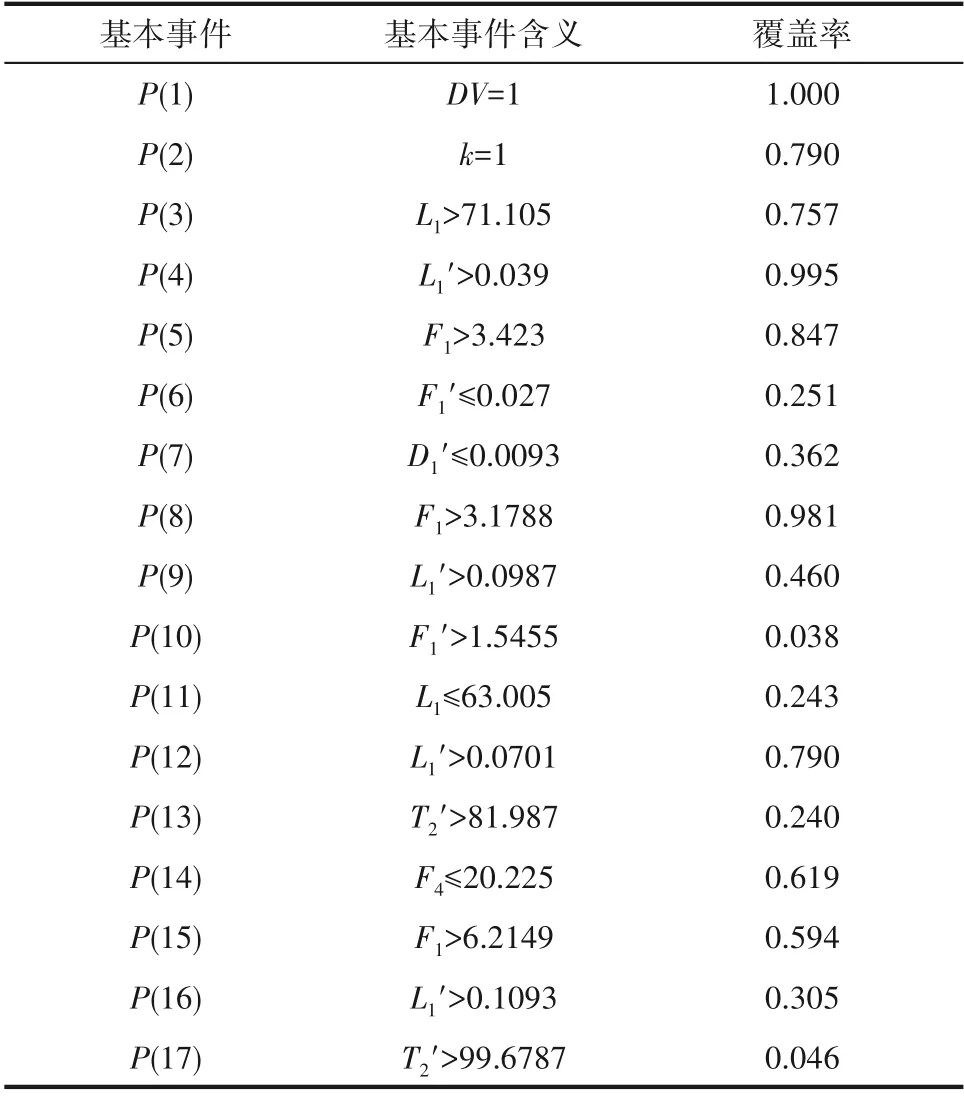
表5 基本事件覆盖率Table 5 Coverages of events

表6 规则覆盖率Table 6 Coverages of rules

四种检测模式能够反映所有训练集中的故障状态，对于汽包过程故障和正常的误判都将影响报警结果，因此在测试集中计算各模式的准确率[39]，如表8所示。

表7 故障发生概率Table 7 Fault Probabilities

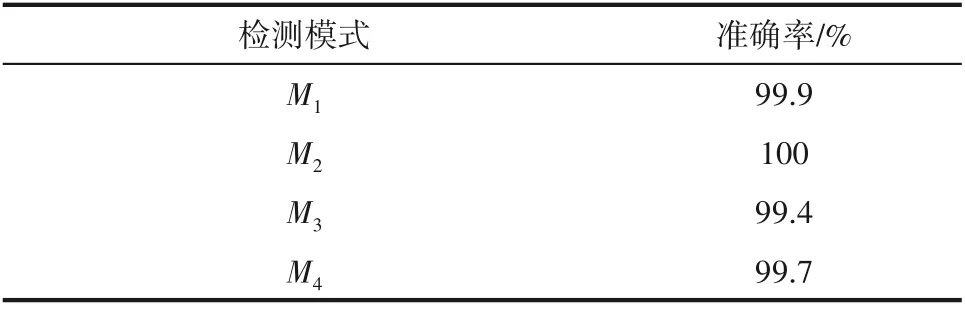
表8 模式准确率Table 8 Accuracies of patterns

从过程控制方面，根据表7的实验结果，操作工人需要预防概率较大的规则发生情况，避免最终引发故障。如表9所示，相比较于传统方法，采用本文提出的ELAD 模型能够排除冗余规则，对混杂系统故障类别的识别正确率可以达到99.8%，获得可以解释的规则信息，取得令人满意的分类结果，增强了汽包过程对于故障的检测能力。

表9 与传统分类模型的性能比较Table 9 Performance comparisons with traditional classifiers

4 结 论

通过结合灰色关联度选择过程变量并引入固定窗口的动态标准差挖掘波动趋势信息，从而优化数据逻辑分析在面向工业过程混杂系统时提取规则的选择问题，提出一种扩展数据逻辑分析方法，能够在不需要专家干预的情况下生成基于数据的可解释模型，能够准确描述不同的观测集并且提供便于理解的因果关系并将模型应用于故障检测。应用于工业煤气化汽包过程的实验结果表明在提取模式和故障检测方面的有效性，所提出模型在不依赖于丰富的专家知识的情况下有效降低了规则的复杂程度，获得面向混杂过程的高效检测模型并丰富了故障信息，提高了对于模型的解释能力。

将来重点研究对于变量之间在不同生产状态下产生偏移的规则提取，并且考虑变量的时滞情况，提取故障发生前期的知识，从而实现对于故障预警能力的提升。