熔盐吸热管瞬态传热特性的数值研究

沈向阳，丁静，陆建峰

（1 仲恺农业工程学院机电工程学院，广东广州510225； 2 中山大学材料科学与工程学院，广东广州510006）

引 言

吸热器是太阳能热发电系统中光热转化的关键部件，主要功能是吸收由定日镜反射过来的太阳辐射能，并将其转化为热能传递给传热工质[1]。聚光型太阳能热发电吸热器主要有容积式吸热器、腔式吸热器和外圆柱吸热器等[2]。吸热器在运行中会频繁地经历启动、云遮和停机过程[3-4]，吸热器吸热管的壁面和管内流体温度随时间变化而变化[5-6]，瞬态过程中的传热特性及运行控制策略对整个太阳能热发电具有重要意义。

吸热器瞬态传热直接影响太阳能热发电系统的安全可靠和功率特性[7]，因此，国内外学者对其开展了大量研究。在容积式吸热器瞬态传热方面，Wu等[8]利用瞬态耦合模型研究了陶瓷泡沫容积式吸热器在热通量突增、热通量突降和热通量阶跃变化的传热特性。Wang等[9]模拟了多孔介质吸热器瞬态响应特性。Ribeiro等[10]用非热平衡法研究了容积式吸热器瞬态特性。Najafabadi 等[11]按照瞬态变化条件通过算法控制自动调节吸热器口缝隙大小以保持吸热器温度基本稳定。在腔式吸热器瞬态传热方面，屠楠等[12]对腔式吸热器在冷启动、温启动和热启动过程中的热性能进行了数值研究，得到了吸热器启动过程中热效率及热损失的变化曲线。张强强等[13]通过模拟实验研究了云遮对熔盐腔式吸热器的热性能影响，并对传递函数法应用于腔式吸热器动态测试进行了理论分析[14]。Samanes 等[15]利用有限容积法对PS10腔式吸热器进行了模拟，通过模拟预测不同结构腔式吸热器长期运行的瞬态特性。Schöttl 等[16]利用相对少光学设置和后续插值的模拟新方法进行腔式吸热器热通量分布的瞬态评估。在外圆柱吸热器瞬态传热方面，王楚航[17]分别模拟了吸热器系统恒功率启动和输入功率阶跃下降时管壁及熔盐温度变化情况。Li等[18]研究了吸热器直接充满和S 型充满、有持续云层时表面温度变化情况。国外学者也对云遮影响下外圆柱吸热器瞬态传热性能进行了模拟[19-21]，得到熔盐出口温度随云层移动或热通量突变的变化关系，并利用闭环目标策略维持吸热器连续安全运行[22-23]。此外，Terdalkar等[24]对水-蒸汽式吸热器进行了瞬态模拟，为吸热器运行模式优化提供理论基础。

聚光型太阳能热发电吸热器瞬态传热研究主要集中在云层遮挡和启动过程方面，且大多针对吸热器整体研究，其研究是吸热器整体变化规律，不能得到局部温度等参数瞬态变化特性。熔盐具有使用温度高、热稳定性和传热性能好等优点，被广泛应用于太阳能热发电系统中作为吸热器传热、蓄热介质[25]；熔盐吸热器是由吸热管组成，高热通量熔盐吸热器热通量和流速同时变化实验在太阳能热发电示范装置中较难操作，而局部单个吸热管瞬态传热特性的研究报道尚属少见。本文通过实验数据验证了吸热管瞬态传热计算模型的可靠性，分析太阳能热发电吸热管在管外壁热通量突变、熔盐流速突减、管外壁热通量和熔盐流速同时突减情况下管壁导热和管内对流传热的瞬态特性，为太阳能吸热器设计和运行控制提供指导。

1 流动与传热模型

1.1 物理模型

吸热管瞬态传热时，管外壁热通量qow为均匀热通量，因此其管内流动与传热为轴对称分布，可以将问题简化为轴对称模型，熔盐水平流动方向为x方向，吸热管半径方向用r 表示，具体模型如图1 所示。其中吸热管长为1.30 m，管径为φ0.02 m×0.002 m。

1.2 数学模型

吸热管内采用k-ε 湍流模型方程，为了简化问题，做如下假设：（1）吸热管内熔盐满足牛顿内摩擦定律，为牛顿流体；（2）管内熔盐在周围壁面上满足无滑移边界条件；（3）流体不可压；（4）流体受迫流动，管入口处截面的流体流速和温度均匀。通过以上假设，吸热管内流动与传热控制方程如下：

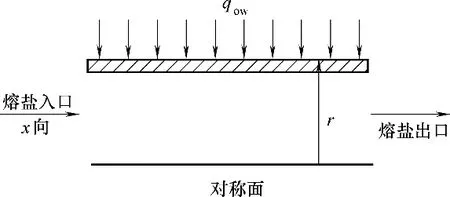
图1 吸热管瞬态传热的物理模型Fig.1 Physical model of receiver tube with transient heat transfer

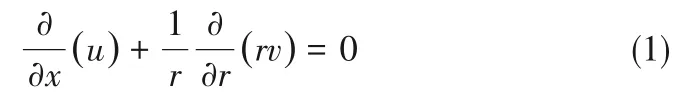
动量守恒方程：

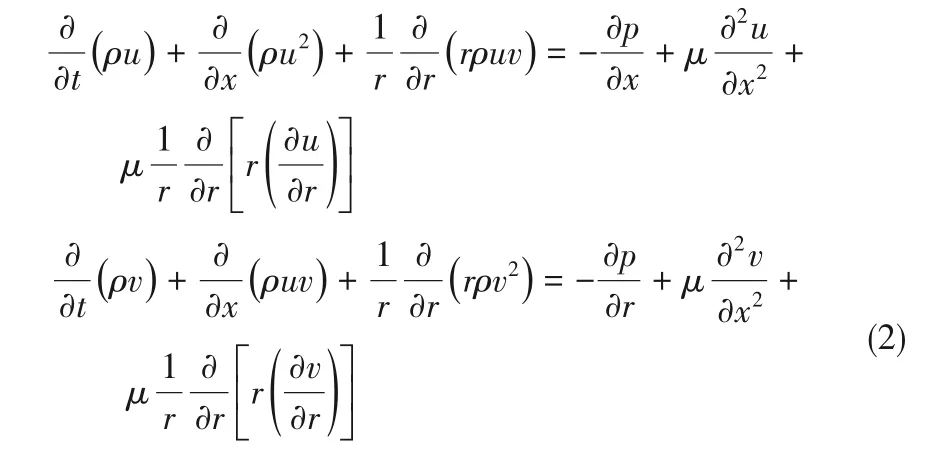
能量守恒方程：

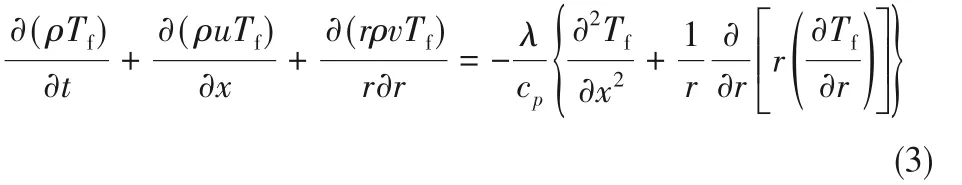
式中，u、v分别为速度在x、r方向上的分量，m/s；ρ 为熔盐密度，kg/m3；μ 为动力黏度，Pa·s；p 为压强，Pa；Tf为管内熔盐温度，℃；λ 为熔盐热导率，W/(m·℃)；cp为熔盐比热容，J/(kg·℃)；r为径向坐标，m；t为时间，s。

吸热管壁导热对管内熔盐瞬态对流传热影响较大，因此需考虑管壁导热的影响，管壁的导热微分方程为[26]：

式中，ρw为管壁材料密度，kg/m3；cp,w为管壁材料比热容，J/(kg·℃)；T 为管壁温度，℃；λT为管壁材料热导率，W/(m·℃)；div(grad T)是温度的Laplace 算子∇2T。

1.3 物性参数和边界条件

吸热管的管壁材料为不锈钢316 L，密度为7980 kg/m3，热导率为18.4 W/(m·℃)，比热容为502 J/(kg·℃)[27]。吸热管内熔盐为三元硝酸混合熔盐（53%KNO3-40%NaNO2-7%NaNO3，质量分数），凝固点为142℃，工作温度范围为250～500℃。熔盐密度、热导率、比定压热容、黏度与温度的关系可用式(5)～式(8)表示[28]：

式中，熔盐温度Tf范围为200～500℃。

吸热管传热过程是单相热传导与对流耦合过程，管壁为固壁无滑移条件，外壁面为等热通量，即：u=0，v=0，qow=q0；入口边界条件：uin=u0，vin=0。

1.4 数值计算方法

采用ANSYS FLUENT15.0进行吸热管瞬态传热计算。计算对象的网格由GAMBIT2.3 划分。吸热管内和管壁均采用四边形网格，管内壁面边界层加密，网格总数为9100。采用分离隐式求解器对瞬态流动传热进行求解，计算中熔盐流速运用绝对速度。利用有限容积法对控制方程进行离散，用SIMPLE算法对压力-速度进行耦合迭代。

2 实验系统及模型可靠性验证

2.1 实验系统

实验系统主要由熔盐罐、熔盐泵、流量计、吸热管、变压器和蒸汽发生器等组成，实验流程图如图2所示。

图2 实验流程图Fig.2 Experimental system

实验采用三元硝酸混合熔盐作为蓄热传热工质，熔盐在熔盐罐1内由电加热器加热到熔点142℃并继续加热至吸热管5所需的入口温度，由熔盐泵2送至吸热管5，熔盐流入吸热管5 由变压器6 加热进行传热实验，再流回熔盐罐1 形成回路，当熔盐罐1温度升高时开启蒸汽发生器7，并控制好熔盐及冷却水流量，维持熔盐罐1 的温度基本稳定。实验吸热管管长及管径同物理模型，实验采用低电压大电流变压器的输出端短路吸热管加热。

数据采集系统由计算机、Agilent 34972A数据采集仪和K 型热电偶（测量吸热管外壁温和管内熔盐温度）组成；所用热电偶均和数据采集仪一起用标准的仪表校准，误差0.5℃。熔盐流量测量通过量程为0～5 m3/h、精度2.5 级的LG 压差流量计测得。吸热管两端的电压通过万用表测量，可精确至0.01 V；通过吸热管的电流利用变压器自带的电流表测量，测量范围0～2000 A，测量精度±0.5%。

2.2 数据处理

吸热管内平均热通量qav[29]为：

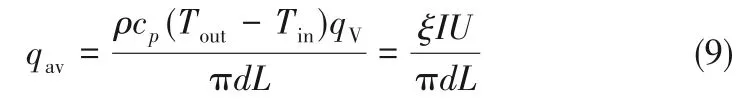
式中，d 为吸热管内径，m；L 为吸热管长，m；qV为平均体积流量，m3/s；I为流过吸热管的电流，A；Tin为熔盐入口温度，℃；Tout为熔盐出口温度，℃；U 为吸热管两端的电压，V。热损失修正系数ξ的不确定性为2%，因此计算中ξ=98%。

2.3 模型可靠性验证

实验吸热管有效传热段1.30 m，熔盐入口温度Tin为301.1℃，入口流速uin为2.98 m/s，管外壁热通量qow由0 突增至201.8 kW/m2。熔盐出口温度（截面平均温度）模拟值为Tout,simul，出口温度实验值为Tout,exp。瞬态传热过程中吸热管熔盐出口温度的模拟值和实验值比较如图3所示。

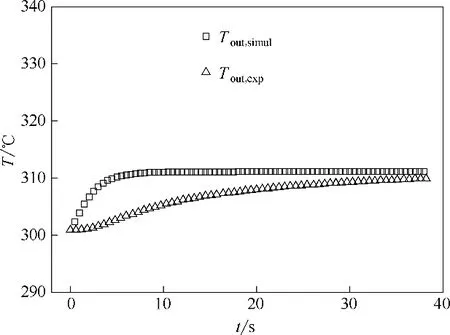
图3 熔盐出口温度的模拟值和实验值Fig.3 Outlet temperature of molten salt with simulation and experiment

由图3 可知，吸热管熔盐出口温度的模拟值与实验值变化趋势一致，均先增加后趋于平稳，熔盐出口温度实验值在瞬态开始4.0 s 后才迅速增加，且增加速率比出口温度模拟值的增加速率小，稳定后的出口温度实验值为309.9℃，比稳定后出口温度模拟值（311.1℃）略小。熔盐出口温度实验值在瞬态初期基本不变的主要原因是：（1）测量熔盐出口温度的热电偶外套金属套管，测量过程中，熔盐的温度变化先传给金属套管，然后再传给热电偶，因此会出现测量滞后；（2）实验管未加热时管壁温度低于管内熔盐温度，加热后管壁温度超过熔盐温度即向熔盐传热需要一定的时间。

瞬态传热过程熔盐出口温度的模拟值比实验值变化快，主要原因是热电偶测温滞后，其次是模拟瞬态传热过程在壁面绝热边界条件下进行（实验中吸热管向保温棉传递的热量较少，模拟计算时可忽略），而实际实验中外壁面外有保温层，保温棉需吸收一部分热量。瞬态稳定后吸热管熔盐出口温度模拟值与实验值偏差仅为0.39%。

3 吸热管瞬态传热特性分析

3.1 管外壁热通量突增

熔盐入口温度301.1℃，入口流速2.98 m/s，吸热管外壁热通量qtran由0突增至201.8 kW/m2即qtran=0→201.8 kW/m2，0.5、1.0、2.0、3.0、12.0、14.0 s时，吸热管出口处的管壁和管内熔盐温度沿径向变化如图4所示。由图4可知，随着时间的推移，吸热管外壁最高温度逐渐上升，且12.0 s 后，最高壁温保持稳定不变。t=0.5 s，管外壁温度升高明显，管内壁温度升高较小，随着时间的推移，热量逐渐从管外壁向内壁传递，同时内壁面向管内熔盐传递热量，熔盐温度随壁温上升而逐渐上升，且靠近管内壁的熔盐温度比管中心升高快。12.0 s 后，吸热管内熔盐温度亦达到稳定。

吸热管qtran=0→201.8 kW/m2，0.5、1.0、2.0、3.0、12.0、14.0 s时，管内中心熔盐温度Tf0及r=0.009 m 处管壁温度Tw'沿轴向（即x 轴，熔盐流动方向）的变化如图5所示。

图4 吸热管出口处管壁和管内熔盐温度变化（qtran=0→201.8 kW/m2）Fig.4 Temperature responses of wall and molten salt at outlet(qtran=0→201.8 kW/m2)

由图5 可知，0.5 s 时管中心熔盐温度Tf0及r=0.009 m 处管壁温度T'w沿轴向基本不变，1.0、2.0、3.0、12.0、14.0 s时Tf0及T'w沿轴向逐渐升高。主要原因是管外壁热通量一定，0～0.5 s 瞬间吸热管壁和管内熔盐吸收的热量很小，引起管壁和熔盐的温升不明显，随着时间的推移吸热管壁及熔盐吸收的热量增大，引起管壁和熔盐的温升沿轴向提高。图5(a)中，瞬态传热过程中，吸热管入口段0.20 m 内各时间点Tf0变化不明显，x＞0.20 m 时各对应位置的Tf0随时间的推移逐渐升高，t≥12.0 s 后，各对应位置的Tf0保持定值。主要原因是吸热管入口段0.20 m 内，熔盐吸收的热量有限，不足以引起明显的温升。图5(b)中，吸热管入口段0.20 m 内各时间点r=0.009 m处管壁温度变化较快，x＞0.20 m 后T'w沿轴向温升变化平缓。随着时间的推移各对应位置的T'w逐渐升高，t≥12.0 s 后，各对应位置的T'w基本稳定。主要原因是吸热管入口段流动的影响引起入口段管内传热系数增大，造成入口段管内壁面温度较低。x＞0.20 m时流动稳定，同一时间点传热系数基本相等，管内熔盐温度升高，因此管壁温度也随之平缓升高。

qtran=0→201.8 kW/m2的瞬态传热过程中，吸热管熔盐出口温度Tout和x=0.65 m 处外壁面温度Tow、外壁面与内壁面温差Tow-Tw及内壁面与管内中心熔盐温差Tw-Tf0的变化如图6所示。

图5 管内中心及管壁的温度变化（qtran=0→201.8 kW/m2）Fig.5 Temperature responses of tube center and wall(qtran=0→201.8 kW/m2)

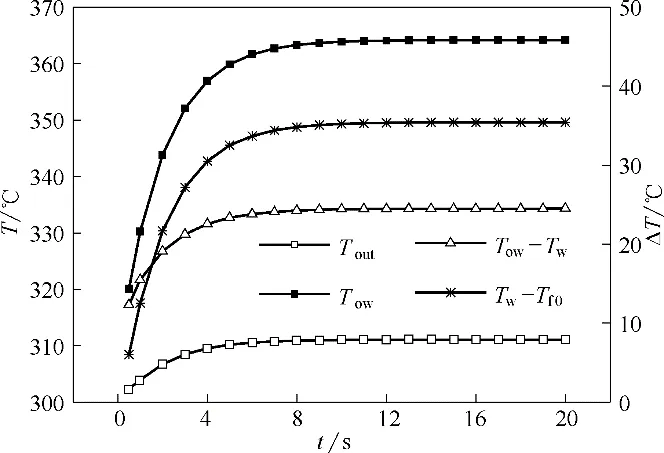
图6 Tout及x=0.65 m处Tow、Tow-Tw和Tw-Tf0的变化（qtran=0→201.8 kW/m2）Fig.6 Temperature responses of Toutand Tow,Tow-Tw,Tw-Tf0at x=0.65 m(qtran=0→201.8 kW/m2)

由图6 可知，同一时刻，管外壁Tow温升速率比Tout温升快。Tout、Tow、Tow-Tw、Tw-Tf0随时间的推移逐渐增大，其中瞬态前期增大速率较快，随着时间推移增大速率逐渐减慢，t≥12.0 s 后，各温度及温差基本稳定。

3.2 管外壁热通量突降

吸热管外壁热通量由201.8 kW/m2突然降至100.9 kW/m2即qtran=201.8→100.9 kW/m2（热通量减半），0、0.5、1.0、2.0、3.0、12.0、14.0 s 时，吸热管内中心熔盐温度Tf0及r=0.009 m 处管壁温度T'w沿x轴向的变化如图7 所示。由图7 可知，吸热管内中心熔盐温度Tf0及r=0.009 m 处管壁温度T'w沿轴向逐渐升高，随着时间的推移升高速率减小；同一x值，Tf0及T'w逐渐降低，t≥12.0 s 后，各对应位置的Tf0和T'w基本稳定。瞬态传热过程中，吸热管入口段0.20 m 内的Tf0和T'w变化速率趋势同qtran=0→201.8 kW/m2。

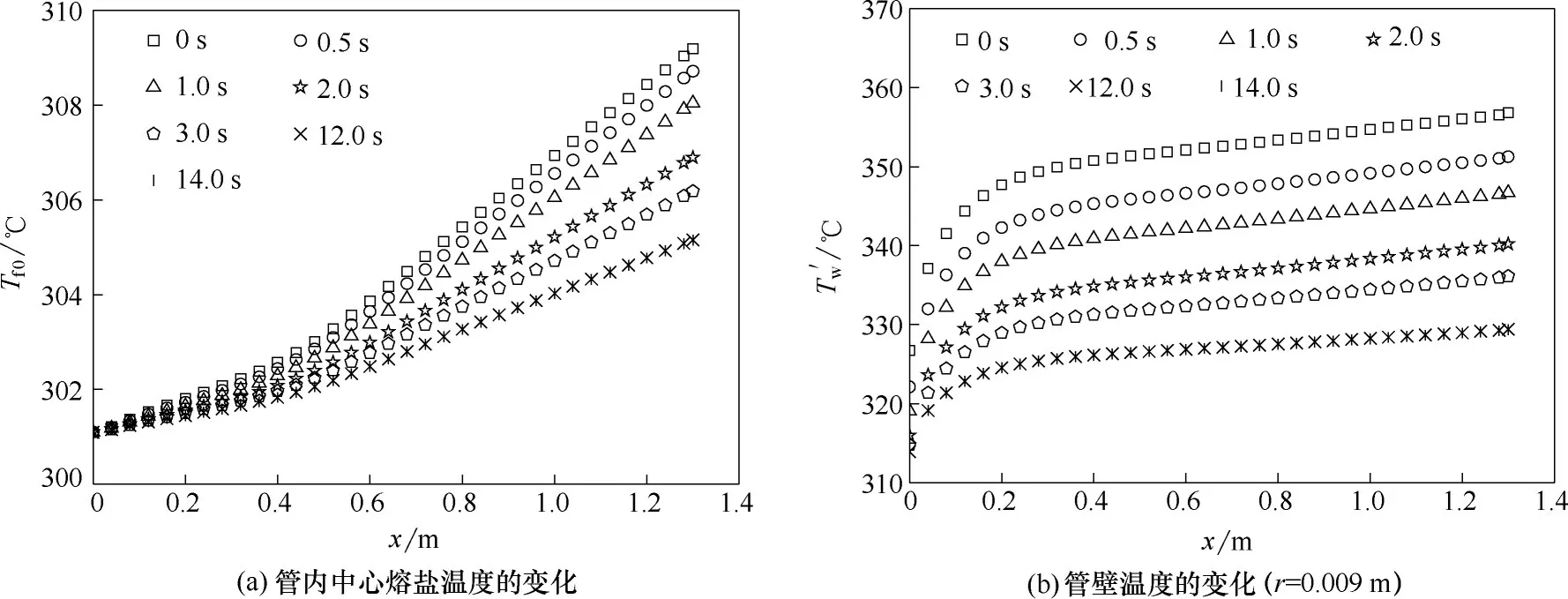
图7 管内中心熔盐及r=0.009 m处管壁的温度变化（qtran=201.8→100.9 kW/m2）Fig.7 Temperature responses of tube center and wall(qtran=201.8→100.9 kW/m2)

qtran=201.8→100.9 kW/m2的瞬态传热过程中，吸热管Tout和x=0.65 m 处Tow、Tow-Tw及Tw-Tf0的变化如图8所示。

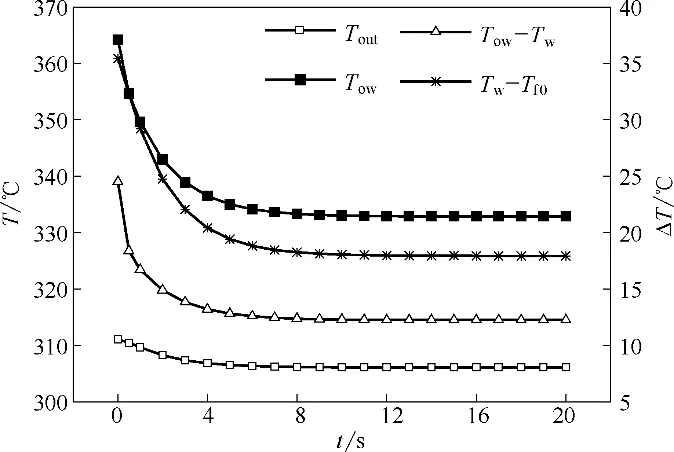
图8 Tout及x=0.65 m处Tow、Tow-Tw和Tw-Tf0的变化（qtran=201.8→100.9 kW/m2）Fig.8 Temperature responses of Toutand Tow,Tow-Tw,Tw-Tf0at x=0.65 m(qtran=201.8→100.9 kW/m2)

由图8 可知，吸热管熔盐出口温度Tout、外壁面温度Tow、外壁面与内壁面温差Tow-Tw、内壁面与管中心熔盐温差Tw-Tf0均随时间的推移逐渐减小，其中瞬态前期减小速率较快，且t=0～0.5 s 内Tow-Tw变化速率比Tw-Tf0变化速率快，随着时间推移两温差减小速率均逐渐减慢，t≥12.0 s 后，两温差基本稳定。稳定后两温差分别约为瞬态开始前各对应温差的一半，因此，管外壁热通量变化对稳态后外壁面与内壁面温差、内壁面与管中心熔盐温差均有影响。吸热管熔盐出口温度在t=0～0.5 s下降速度较t=0.5～1.0 s 慢，主要由于瞬态初期，熔盐吸热量受到瞬态前的影响，热通量变化时即t=0 s，熔盐已吸收到的热量较大，但高温熔盐还没有到达出口，同时吸热管壁温在t=0 s时较高，瞬态初期熔盐可吸收其中部分热量，而t≥0.5 s 时，瞬态前的状态对热通量突降瞬态过程影响减小。

3.3 管内熔盐流速突减

吸热管外壁热通量为100.9 kW/m2（即201.8 kW/m2的一半），管内熔盐流速从2.98 m/s 突然降至1.49 m/s 即uin=2.98→1.49 m/s（熔盐流速减半），0、0.5、1.0、2.0、3.0、12.0、16.0、18.0 s 时，吸热管内中心熔盐温度Tf0沿x轴向的变化如图9所示。

图9 管内中心熔盐温度的变化（uin=2.98→1.49 m/s）Fig.9 Temperature responses of tube center(uin=2.98→1.49 m/s)

由图9 可知，瞬态开始后，同一x 处管中心熔盐温度Tf0增加速率逐渐减小，t≥16.0 s 后，Tf0增加速率趋近于0，吸热管传热达到平衡，对应位置的温度保持定值。流速减小的瞬态传热过程持续时间比仅改变热通量的瞬态传热过程持续时间长，此变化规律与文献[30]实验结果一致。

图10 Tout及x=0.65 m处Tow、Tow-Tw和Tw-Tf0的变化（uin=2.98→1.49 m/s）Fig.10 Temperature responses of Toutand Tow,Tow-Tw,Tw-Tf0 at x=0.65 m(uin=2.98→1.49 m/s)

吸 热 管qow=100.9 kW/m2，uin=2.98→1.49 m/s 的瞬态传热过程中，吸热管Tout和x=0.65 m 处Tow、Tow-Tw及Tw-Tf0的变化如图10 所示。由图10 可知，吸热管熔盐出口温度Tout、外壁面温度Tow和内壁面与管中心熔盐温差Tw-Tf0均随时间的推移逐渐增大，其中瞬态前期增大速率较快，t≥16.0 s，Tout、Tow和Tw-Tf0都基本稳定。稳态后的Tout与uin=2.98 m/s、qtran=0→201.8 kW/m2（两倍熔盐入口流速和两倍管外壁热通量）瞬态稳定后的Tout较接近；稳态后Tow比uin=2.98 m/s、qtran=0→201.8 kW/m2瞬态稳定后的Tow低15.7℃，而Tw-Tf0比uin=2.98 m/s、qtran=0→201.8 kW/m2瞬态稳定后的Tw-Tf0高7.3℃。由图10 还可知，瞬态传热过程中，管外壁与管内壁温差Tow-Tw随着时间的推移先降低后升高，原因是管内熔盐流速突然降低，管内传热系数减小，管内壁温度上升，而管外壁在较短时间内温升有限，因此Tow-Tw先降低；t≥16.0 s，Tow-Tw也基本稳定，稳定后Tow-Tw与瞬态开始前的Tow-Tw基本一致，因此仅仅熔盐入口流速变化对瞬态前后的管外壁与管内壁温差无影响。

3.4 管外壁热通量及管内流速同时突减

熔盐入口温度301.1℃，吸热管外壁热通量qtran=201.8→100.9 kW/m2，同时熔盐入口流速uin=2.98→1.49 m/s，0、0.5、1.0、2.0、3.0、4.0、16.0、18.0 s时，吸热管内中心熔盐温度Tf0沿x 轴向的变化如图11 所示。由图11 可知，瞬态传热过程中，x＞0.20 m 时各对应位置Tf0随时间推移先升高后降低，x值越大，变化越明显，t≥16.0 s 后，各对应位置的Tf0保持定值。原因是吸热管热通量突然减小的同时流速也减小，瞬态开始时，管内熔盐已吸收了qtran=201.8 kW/m2稳定后的热量，当流速减小，熔盐继续吸收热通量减小时的加热量及管壁余留热量，瞬态前期单位质量熔盐吸收的热量增加；瞬态后期，由于热通量小，单位质量熔盐吸收的热量减小，因此管内中心熔盐温度Tf0先升高后降低；到达稳态后单位质量熔盐吸收的热量达到定值且与瞬态开始前吸收热量相近，因此瞬态结束后管内中心熔盐温度保持定值且与瞬态开始前熔盐温度接近。

图11 管内中心熔盐温度的变化（qtran=201.8→100.9 kW/m2，uin=2.98→1.49 m/s）Fig.11 Temperature responses of tube center(qtran=201.8→100.9 kW/m2，uin=2.98→1.49 m/s)

吸热管qtran=201.8→100.9 kW/m2同时uin=2.98→1.49 m/s 的瞬态传热过程中，吸热管Tout和x=0.65 m处Tow、Tow-Tw及Tw-Tf0的变化如图12 所示。由图12可知，x=0.65 m 处管外壁温度Tow、外壁面与内壁面温差Tow-Tw随时间的推移迅速降低最后趋于稳定，稳定后的Tow-Tw为12.3℃，而瞬态开始前对应的Tow-Tw为24.5℃，瞬态结束后的温差值约为瞬态开始前的一半，因此，稳态后外壁面与内壁面温差与管外壁热通量变化呈正比，可用式（10）表达。管内熔盐出口温度Tout、管内壁面与管内中心熔盐温差Tw-Tf0均随时间的推移先升高再降低，t≥16.0 s 后趋于稳定，稳定后的Tout值和瞬态开始前的Tout基本相等，Tw-Tf0值比瞬态开始前小。因此当吸热管外壁面热通量突然降低时，可通过适当减小熔盐流速来控制熔盐出口温度基本稳定。

式中，qtran,b、qtran,s分别为瞬态开始前和稳定后的管外壁热通量，kW/m2；Tow,b、Tw,b分别为瞬态开始前的管外壁和管内壁温度，℃；Tow,s、Tw,s分别为瞬态稳定后的管外壁和管内壁温度，℃。

由式（10）可得瞬态稳定后和开始前的管外壁热通量比为式（11）：

图12 Tout及x=0.65 m处Tow、Tow-Tw和Tw-Tf0的变化（qtran=201.8→100.9 kW/m2，uin=2.98→1.49 m/s）Fig.12 Temperature responses of Toutand Tow,Tow-Tw,Tw-Tf0 at x=0.65 m(qtran=201.8→100.9 kW/m2，uin=2.98→1.49 m/s)

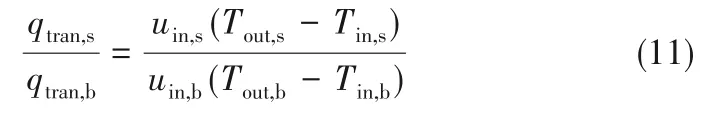
式中，Tin,b、Tout,b分别为瞬态开始前的熔盐进口和出口温度，℃；Tin,s、Tout,s分别为瞬态稳定后的熔盐进口和出口温度，℃；uin,b、uin,s分别为瞬态开始前和稳定后的熔盐入口流速，℃。

瞬态过程中，Tin,s=Tin,b，因此，瞬态稳定后吸热管熔盐出口温度Tout,s为

式（12）为瞬态传热过程中吸热器熔盐出口温度控制提供理论依据。

4 结 论

通过实验验证了吸热管瞬态传热数值计算模型的可靠性，利用数值模拟方法研究了管外壁热通量突变、熔盐流速突减、管外壁热通量和熔盐流速同时突减对吸热管瞬态传热特性的影响规律，得到如下结论。

（1）管外壁热通量突变（突增或突减）时，吸热管入口段0.20 m 内，各时间点管内中心熔盐温度Tf0变化不明显，但管壁温度T'w变化较快。吸热管熔盐出口温度Tout、外壁面温度Tow、外壁面与内壁面温差Tow-Tw、内壁面与管中心熔盐温差Tw-Tf0在瞬态前期变化（增大或减小）速率较快，随着时间推移变化速率逐渐减慢，最后达到稳定。

（2）管内熔盐流速突减时，吸热管Tout、Tow和Tw-Tf0均随时间的推移逐渐增大，稳态后的Tow比两倍熔盐入口流速和两倍外壁热通量瞬态稳定后Tow小。Tow-Tw随着时间的推移先降低后升高，稳定后Tow-Tw与瞬态开始前的Tow-Tw基本一致。熔盐流速突变的瞬态传热过程持续时间比管外壁热通量突变的瞬态传热过程持续时间长。

（3）吸热管外壁热通量和管内熔盐流速同时减半时，Tf0、Tout随时间的推移先升高后降低，稳态后Tf0和Tout保持定值且与瞬态开始前对应温度接近。因此吸热管外壁面热通量突然变化时，可通过改变适当的熔盐流速来控制熔盐出口温度基本稳定。

（4）吸热管稳态后的Tow-Tw与管外壁热通量变化呈正比，与熔盐流速变化无关；而Tw-Tf0与管壁热通量及流速变化均有关。

符 号 说 明

cp——熔盐比热容，J/(kg·℃)

D——吸热管外径，m

d——吸热管内径，m

I——流过吸热管的电流，A

L——吸热管长，m

qav——管内壁平均热通量，kW/m2

qtran——管外壁瞬态热通量，kW/m2

qtran,b——瞬态开始前管外壁热通量，kW/m2

qtran,s——瞬态稳定后管外壁热通量，kW/m2

qV——平均体积流量，m3/s

r——径向坐标，m

Tf——管内熔盐温度，℃

Tf0——吸热管中心熔盐温度，℃

Tin——熔盐入口温度，℃

Tin,b——瞬态开始前熔盐入口温度，℃

Tin,s——瞬态稳定后熔盐入口温度，℃

Tout——熔盐出口温度，℃

Tout,b——瞬态开始前熔盐出口温度，℃

Tout,s——瞬态稳定后熔盐出口温度，℃

Tow——吸热管外壁温度，℃

Tow,b——瞬态开始前管外壁温度，℃

Tow,s——瞬态稳定后管外壁温度，℃

Tw——吸热管内壁温度，℃

Tw,b——瞬态开始前管内壁温度，℃

Tw,s——瞬态稳定后管内壁温度，℃

T'w——r=0.009 m管壁温度，℃

U——吸热管两端的电压，V

uin——熔盐入口流速，m/s

uin,b——瞬态开始前熔盐入口流速，m/s

uin,s——瞬态稳定后熔盐入口流速，m/s

下角标

av——平均值

f——熔盐

f0——管中心熔盐

in——熔盐入口

out——熔盐出口

ow——管外壁

w——管内壁