液固流态化动态过程中相间作用力的数值模拟及实验验证

张仪，李兵，白玉龙，张锴

（华北电力大学热电生产过程污染物监测与控制北京市重点实验室，北京102206）

引 言

液固流化床凭借其良好的颗粒混合与热质传递特性已在化工、能源和环保等诸多领域得到广泛应用[1-2]。针对实际过程中不可避免的开、停车及变工况运行状态，充分理解操作速度突变后床内流动、传递及反应的动态特性对液固流化床放大设计和优化操作具有重要的指导意义。Slis 等[3]较早将Richardson 等[4]针对稳态操作条件下流化速度与整体固含率的关联式扩展到动态过程，获得了床内颗粒速度表达式；随后Fan 等[5]、Gibilaro 等[6]、Asif 等[7]、Thelen 等[8]和Liu 等[9]提出了描述液固体系动态特性的各自模型；尤东光等[10]进而考察了操作速度变化对颗粒浓度时空分布的影响行为，阐述了液固流化床中浓-稀相界面的变化规律。近三十年来，CFD（computational fluid dynamics）方法已成为流态化研究的一种重要工具，其中基于欧拉-欧拉的双流体模型因具有剖析大型装置内复杂多相流动时空特性的显著优势而被广泛关注，例如Chen 等[11]和Zhang 等[12-13]通过再现液固流化床的膨胀与收缩特性验证了Dallavalle 曳力模型[14]的可靠性。大量研究结果表明相间作用力是双流体模拟的关键因素[15]，理论上包括曳力、升力、虚拟质量力和Basset力等[16]，其中曳力是流体对颗粒动量输运的最主要作用力[17]，升力是颗粒周围非对称性流场和/或颗粒自身旋转导致的横向力[18]，虚拟质量力和Basset 力为颗粒与流体存在相对加速度时受到的非恒定作用力[19-20]。已有研究[21-23]主要关注曳力的影响行为，张仪等[23]评价了Gidaspow 和Syamlal-O’Brien等6个曳力模型对稳态时散式液固流态化的预测性能，发现基于PR-DNS（particle-resolved direct numerical simulation）方法提出的曳力模型因忽略颗粒间相互作用而性能较好；有些学者探讨了其他相间作用力影响行为，例如Zbib 等[24]发现颗粒所受曳力比虚拟质量力大4 个量级，考虑虚拟质量力与否对床层膨胀高度影响极小；Koerich 等[25]认为升力在一定程度上影响床层宏观特性，然而上述研究皆限于液固体系的稳定流化状态。鉴于动态过程与稳态过程非均匀浓度场及颗粒非平衡运动[3,6,9]等本质差异，需要对曳力模型及其他相间作用力模型进一步探讨。为此，本文以水-玻璃珠体系实验为基础，通过对稳态操作条件下实验结果的有效性验证，在基于颗粒动理学理论的欧拉双流体框架内考察曳力模型对床层收缩和膨胀特性数值模拟的影响规律，进而探讨了升力模型影响行为及相间作用力影响机制，旨在对液固流化床的合理设计与优化运行提供必要的理论支撑。

1 实验及其验证

液固流态化实验装置如图1 所示，其中有机玻璃制成的矩形流化床高为1000 mm，横截面为300 mm × 25 mm；为确保入口液体的均匀性，分布器采用固定床与烧结板相结合形式，固定床高为200 mm，其内填充直径为6 mm 的玻璃珠。液相采用自来水，在实验工况下密度为997.8 kg·m-3，黏度为9.58×10-4Pa·s；固相采用球形玻璃珠，直径为0.9 ～1.0 mm，密度为2460 kg·m-3。实验过程中使用CCD（charge coupled device）高速相机拍摄流化床内流动特征及床层界面动态变化过程，每次实验重复三次，经图像处理得到入口液速突变后床层收缩或膨胀高度随时间的变化规律。

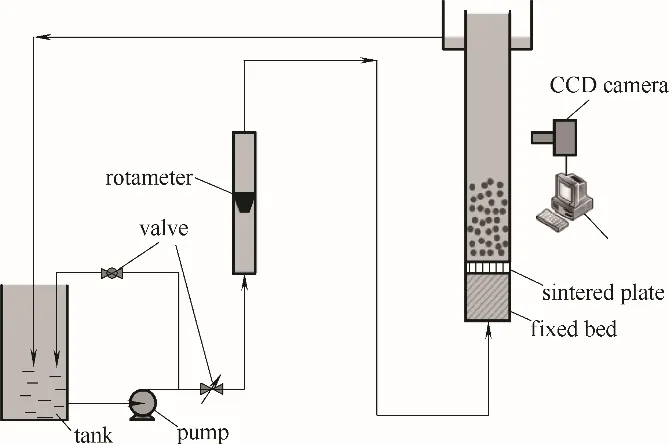
图1 液固流态化实验装置Fig.1 Schematic diagram of experimental setup of liquid-solid fluidization

早在1954年，Richardson等[4]在实验观测结合理论分析基础上提出了稳定流化时操作速度与整体固含率的经验关联式，Felice[26]在总结大量文献基础上对该公式评价为“近半个世纪以来液固流态化领域最重要的研究成果之一”，诸多学者[12,21-22]用来检验测量结果的准确性或数值模型的可靠性，其具体表达式为：

式中，u0和ut分别为操作速度和颗粒终端速度，εs为整体固含率；n 为膨胀指数，可以采用Garside等[27]推荐的关联式计算：

图2给出了床层达到稳定流化状态时实验测量与Richardson-Zaki 公式预测的对比结果。总体而言，两者较为吻合，最大相对误差小于10%，平均相对误差在5%以内，该结果略优于文献[21-22]。但在液体操作速度较低时，两者偏差相对较大，其中操作速度为0.015、0.022、0.029 m·s-1时对应的相对偏差分别为9.0%、7.1%和6.9%，其主要原因是液速较低时床层膨胀相对较浅，导致分布器影响较大，在后续实验中将予以注意。

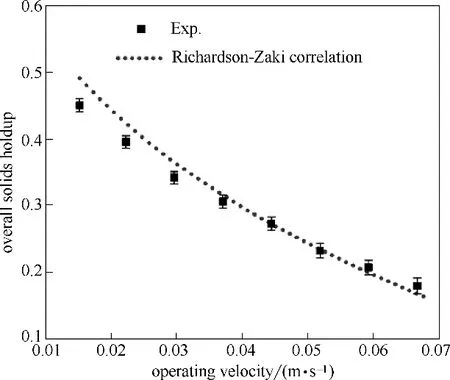
图2 稳定流化状态下整体固含率实验值验证Fig.2 Validation of experimental overall solids holdup in steady fluidization

2 数学模型

2.1 双流体模型

双流体模型将颗粒拟作与流体相互渗透的连续介质，采用形式统一的偏微分方程组描述流体和颗粒两相流动行为，这里动量方程中相间作用力同时考虑了曳力和升力。

连续性方程：

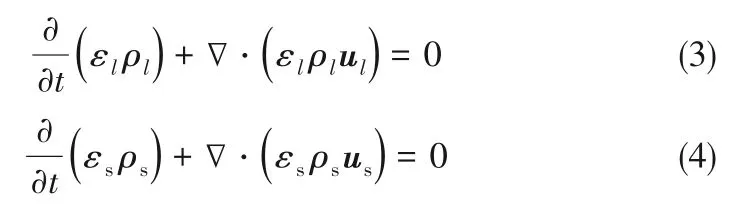
动量方程：

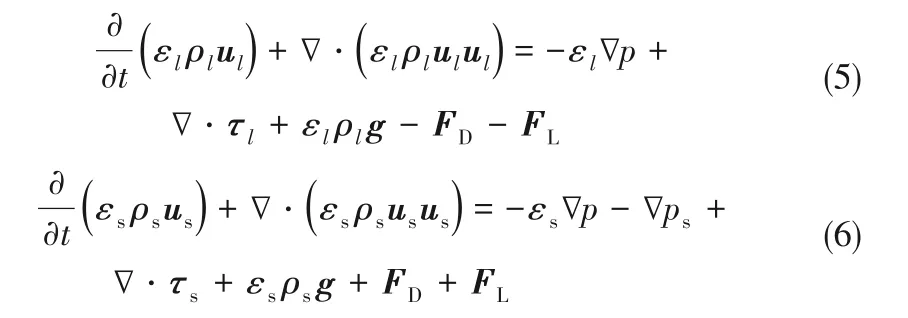
式中，下角标l和s分别代表液相和固相；ε、ρ和p 分别为体积分数、密度和压力；u 和g 分别为速度与重力加速度；FD和FL分别表示曳力和升力；τ是应力张量。

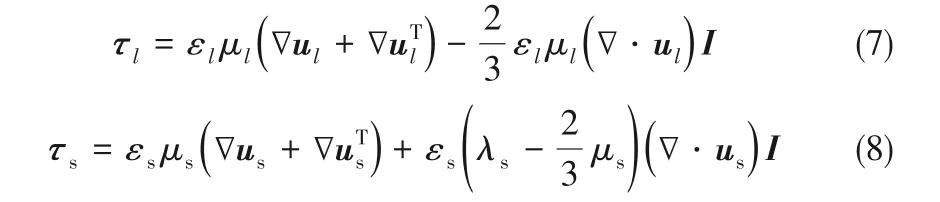
式中，μs和λs分别表示固相剪切黏度和固相体积黏度。本文中固相本构关系采用颗粒动理学理论[28]封闭。

2.2 相间作用力模型

相间作用力模型实现了动量方程中液固两相耦合，本文重点考察曳力和升力两种相间作用力对液固流化床动态特性CFD 模拟的影响行为，具体计算模型概括如下。

2.2.1 曳力模型 曳力通常表达为动量交换系数与相对速度之积：

式中，β为动量交换系数，通过曳力模型计算。

已有的曳力模型主要来源于床层压降和颗粒终端沉降速度等实验测量结果或者采用颗粒解析的直接数值模拟。针对散式液固流态化特征，本研究选取基于实验测量的Wen-Yu[29]、Gidaspow[30]、Syamlal-O’Brien[31]和Dallavalle[14]4 个曳力模型和基于直接数值模拟的TGS 曳力模型[32]，具体表达形式概述如下。

Wen-Yu曳力模型

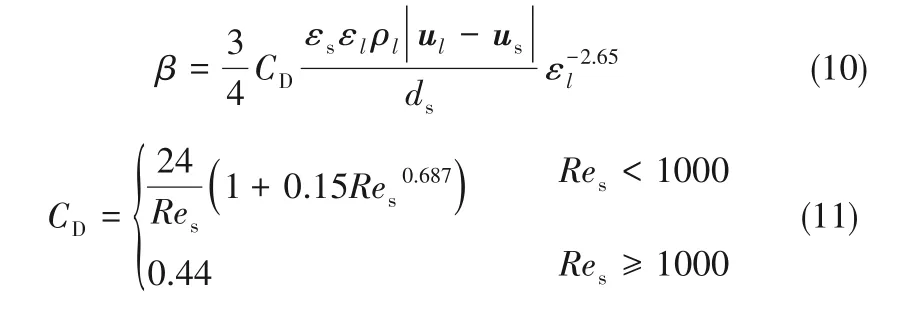
Gidaspow曳力模型

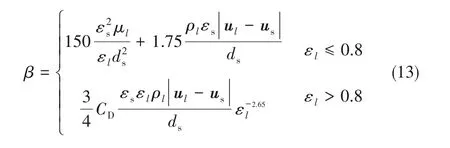
式中，CD计算同式（11）。

Syamlal-O’Brien曳力模型

式中，Res计算同式（12）。

Dallavalle曳力模型

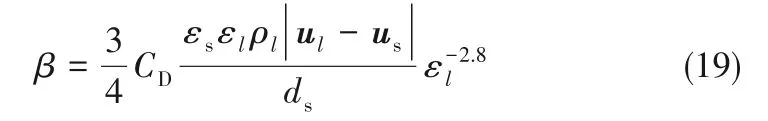
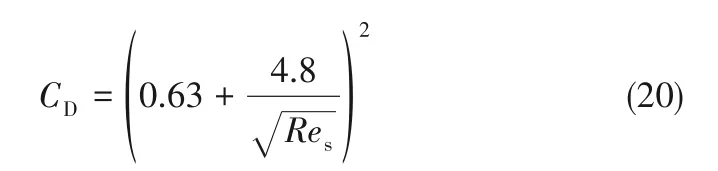
式中，Res计算同式（12）。

TGS曳力模型

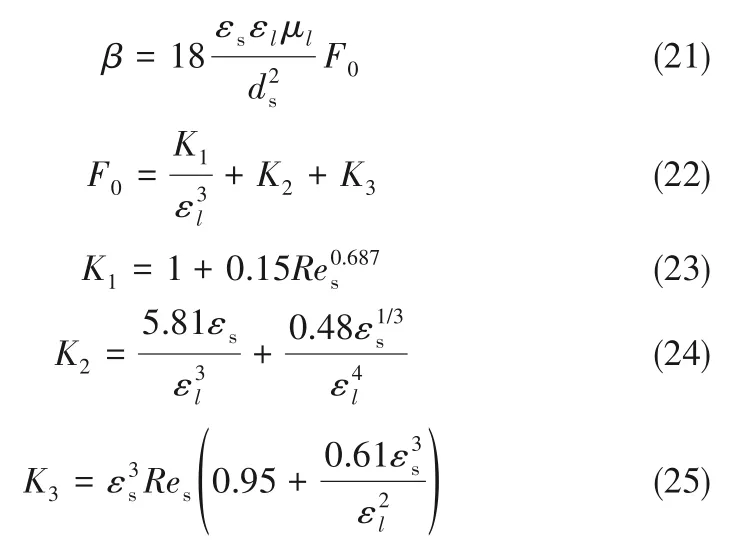
式中，Res计算同式（12）。

2.2.2 升力模型 流体作用于颗粒的升力通常分为Saffman 力和Magnus 力两类[18]，其中Saffman 力是指剪切流动中，与来流方向垂直的颗粒两侧产生了由低流速指向高流速的压力差；Magnus 力为运动的旋转颗粒由于流场非对称所受到的横向力，方向由逆流侧指向顺流侧。但是在实际流动中两种机制同时作用且难以区分，因此，在双流体框架下可以选取的升力表达形式为[33]：

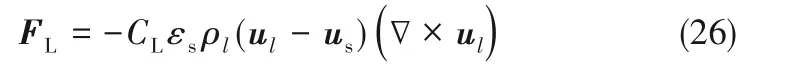
式中，CL为升力系数，由升力模型得到。

已有针对升力模型研究主要集中在气液两相体系[18,33]，在液固体系中关注较少，其中Moraga 等[34]基于实验测定湍流场中作用于固体颗粒的横向力，提出以下升力模型：

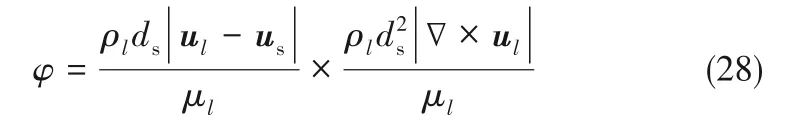
式中，φ为颗粒Reynolds数与旋转Reynolds数之积。

2.3 模拟方法

模拟过程中除颗粒直径（0.9 ～1.0 mm）取其算术平均值0.95 mm 外，其他参数与实验过程相一致。选取的收缩和膨胀过程包括高、低液速各2组工况，实验过程中首先维持床层在稳定流化状态，此刻操作速度记为u0，床层高度为h0；然后关小或开大阀门，操作速度瞬间突变为u1，床层高度开始降低/升高，最终达到h1。具体的初始条件和边界条件见表1和图3。

CFD 模拟过程中压力-速度耦合运用SIMPLE(semi-implicit method for pressure-linked equation)算法，空间与时间离散分别采用二阶迎风格式与二阶隐式格式。构建均匀分布的六面体结构网格，网格尺度为5 mm；时间步长固定为0.002 s；详细的网格与时间步无关性验证见文献[23]。

3 结果与讨论

3.1 床层动态收缩特性

3.1.1 实验与模拟比较 图4 展示了case 1 中液固流化床收缩过程的实验和数值模拟动态结果。初始时刻床层高度为530 mm，由图4(a)的实验结果可以发现，收缩过程中床层表面存在一定波动，历经约8.5 s后床层降至400 mm 的稳定高度处；图4(b)以TGS曳力模型计算结果为例给出了床层颗粒浓度的时间分布，模拟的床层表面十分平整，收缩过程时长约8.0 s且床层高度最终降至395 mm。

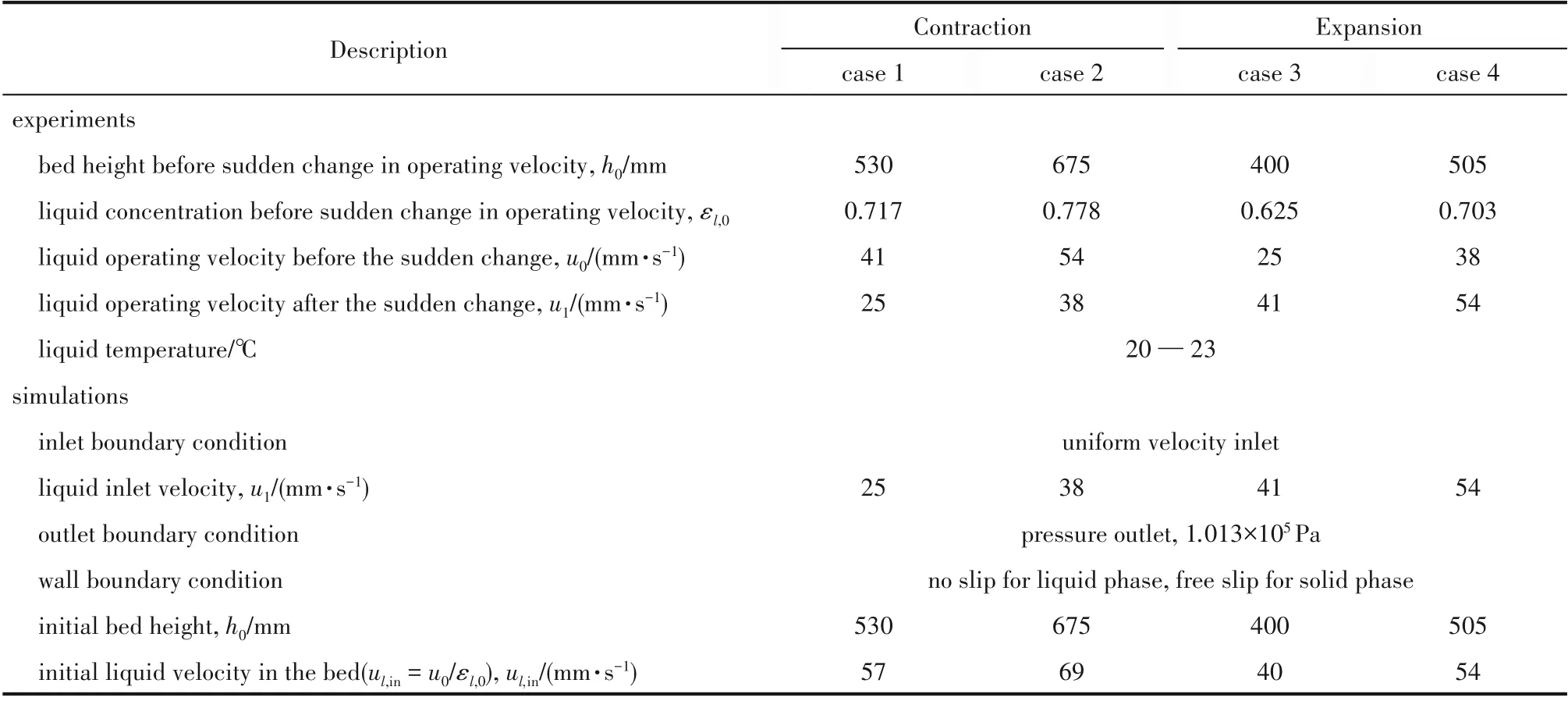
表1 边界条件与初始化设置Table 1 Boundary conditions and initialization settings

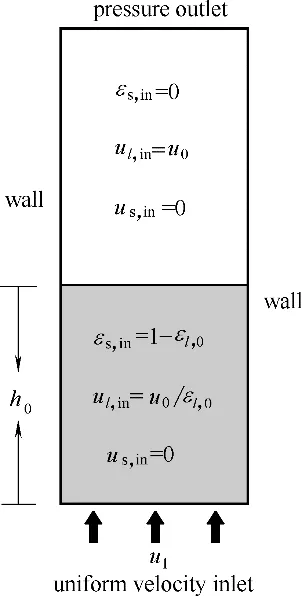
图3 边界条件与初始化设置Fig.3 Schematic diagram of boundary conditions and initialization settings

当操作速度从u0突然降至u1后，处于稳定流化状态的颗粒加速下落，颗粒所受阻力增大导致其加速度减小，极短暂加速运动后颗粒开始匀速下落。悬浮液中颗粒以相同速度同时下落，因此颗粒浓度与床层收缩前保持一致。上述分析适用于流化床内大部分区域，但是床层底部颗粒无法向下运动，上方颗粒持续落入该区域后受较高颗粒浓度影响而所受阻力增大，导致速度降至为零。此时床层底部形成了颗粒浓度为εs,1的“浓相”区，上部则存在着颗粒浓度为εs,0的“稀相”区，浓-稀相间的过渡区域称为“分隔界面”，稀相区持续下落并缩小，浓相区则不断向上扩张，如图4 所示。当上升的分隔界面与下降的床层表面相遇、合并后，收缩过程结束，此时整个床层达到对应于操作速度u1、颗粒浓度为εs,1的平衡状态。

3.1.2 曳力模型对模拟结果影响 考察了Wen-Yu、Gidaspow、Syamlal-O’Brien、Dallavalle 和TGS 5个曳力模型对液固流化床收缩特性的影响。Gibilaro等[6]基于质量守恒提出了描述液固流化床收缩/膨胀过程的理论模型，表达式如下：

式中，Tr表示床层对操作速度突变的响应时间，即动态过程持续时间，下角标0 和1 分别代表动态过程前后的平衡状态。

图5 展示了由Gibilaro 理论和不同曳力模型预测的收缩过程中床层高度的时间分布，Gibilaro理论预测case 1 和case 2 响应时间Tr分别为8.1 s 和11.3 s，与相应的实验测量值8.5 s 和11.5 s 一致性较好，进一步验证了该理论对收缩过程良好的预测能力[10,12,14]。文中部分曳力模型对响应时间的预测与实验值较为接近，其中case 1 中Gidaspow、Syamlal-O’Brien 和TGS 曳力模型的预测结果分别为9.0、9.0和8.0 s，而case 2 中Syamlal-O’Brien 及TGS 曳力模型的预测结果则分别为13.0、9.5 s；其余曳力模型的计算值与测量结果差异较大。

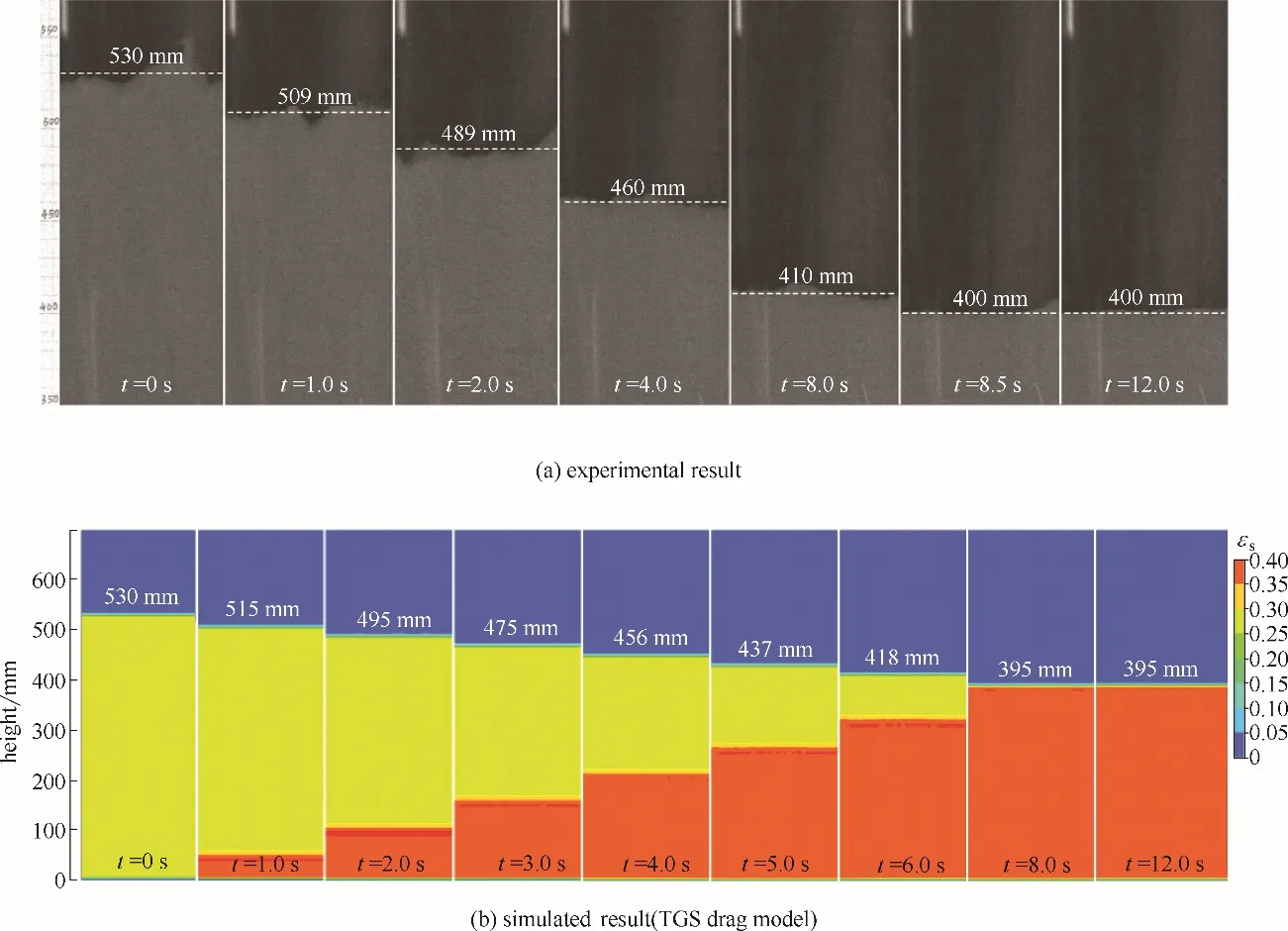
图4 液固流化床的收缩过程Fig.4 Contraction process of liquid-solid fluidized bed(from u0=41 mm·s-1 to u1=25 mm·s-1)

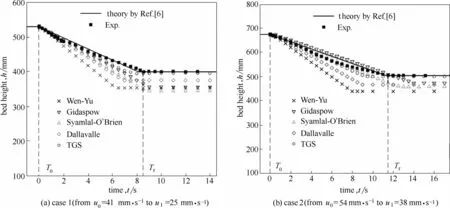
图5 液固流化床动态收缩时的床层高度分布Fig.5 Distributions of bed height in contraction process of liquid-solid fluidized bed

仅考虑响应时间Tr难以充分评价曳力模型对床层动态特性的预测性能，例如case 1 中Gidaspow 和Syamlal-O’Brien 曳力模型的预测结果（9.0 s）与实验测量（8.5 s）仅相差0.5 s，然而床层颗粒浓度却与实验结果存在较大差异。为此，本文将床层整体固含率εs,1纳入考察范畴。表2 汇总了不同曳力模型预测的整体固含率εs,1，其中TGS 曳力模型预测值与实验值的相对偏差在case 1 和case 2 中分别为1.3%和0.9%，其余曳力模型给出的偏差值均超过5%。由综合响应时间Tr和整体固含率εs,1来看，TGS 曳力模型对收缩过程的预测与实验结果较为吻合。

表2 床层收缩过程终止时的整体固含率实验值和模拟值Table 2 Experimental and simulated results of overall solids holdups after contraction process of liquid-solid fluidized bed

图6 升力模型对床层收缩特性的影响Fig.6 Effect of lift force model on contraction processes

3.1.3 升力模型对模拟结果影响 图6展示了收缩过程中升力模型对床层高度随时间分布的影响。在TGS 曳力模型基础上考虑升力模型后，无论在case 1[图6(a)]还是case 2[图6(b)]中，考虑升力模型与否所给出的平衡状态下床层高度h1以及响应时间Tr基本一致，表明选取的升力模型对液固流化床动态收缩特性模拟结果影响可以忽略。

3.2 床层动态膨胀特性

3.2.1 实验与模拟比较 图7 为case 3 中液固流化床膨胀过程的实验和数值模拟结果。初始时刻床层高度为400 mm，实验过程中床层表面不均匀性较为显著，约16.0 s 后膨胀过程基本结束，此后床层在530 mm 高度上下波动。以TGS曳力模型结果为例，图7(b)给出了颗粒浓度的时空演化，膨胀过程中床层表面较为平整，持续约18.0 s 后床层高度上升至520 mm且基本维持稳定。

操作速度从u0突然升至u1后，系统平衡被打破，床层将呈活塞状向上匀速运动。位于活塞底部的任一颗粒一旦在扰动作用下脱离界面，则向下的合力将该颗粒彻底推离活塞，其周围颗粒由于液相浓度增大而不断从活塞中脱落，此机理在活塞开始上升时即起作用。这些颗粒落入下层清液后形成了浓度为εs,1的“稀相”区，上升的活塞悬浮液则对应“浓相”区，颗粒浓度仍然保持εs,0。然而不同于收缩过程，床层膨胀时浓、稀两相“分隔界面”随着时间推移无法维持稳定，如图7(b)所示。相关实验[10]表明床内形成了由浓到稀的过渡段而非分隔界面；而且需要相对较长的响应时间来到达对应于u1的平衡状态。Gibilaro 等[6]认为以上差异源于Rayleigh-Taylor 不稳定性，而Liu 等[9]则归因于颗粒浓度在稀相区的传播速度小于在浓相区。

3.2.2 曳力模型对模拟结果影响 通过对液固体系动态特性的理论分析和CFD 计算，Mazzei 等[35]建立了预测床层膨胀高度的指数模型，表达式如下：

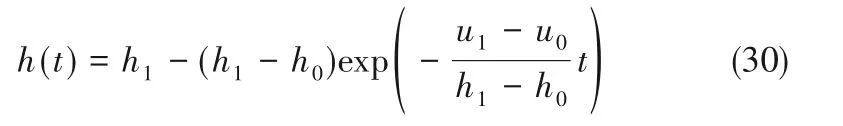
式中，t表示时间，下角标0和1分别代表膨胀过程前后的平衡状态。指数型函数决定了只有当t 趋近无穷时床层高度才能无限接近h1，Mazzei 等[35]建议取h 为95%h1时所对应t 为响应时间，因此Tr可以

图7 液固流化床的膨胀过程Fig.7 Expansion process of liquid-solid fluidized bed(from u0=25 mm·s-1 to u1=41 mm·s-1)

图8 液固流化床动态膨胀时的床层高度分布Fig.8 Distributions of bed height in expansion process of liquid-solid fluidized bed

由式(31)近似获得：

图8 展 示 了 由Mazzei 和Lettieri 模型[35]、Gibilaro理论[6]和典型曳力模型预测的膨胀过程中床层高度随时间的分布情况。Mazzei 和Lettieri 模型给出的指数分布一定程度上再现了真实膨胀过程，然而响应时间较长；Gibilaro理论给出的床层高度随时间分布体现了液固体系的理想膨胀过程，但响应时间较短。实验测量的响应时间Tr在case 3 和case 4 中分别为16 s 和24 s，部分曳力模型给出了较为接近的计算结果：TGS 及Dallavalle 曳力模型在case 3 中计算值分别为18 s 及14 s；TGS、Syamlal-O’Brien 及Gidaspow 曳力模型在case 4 中则分别对应22、20 及19 s。由表3 可知，TGS 曳力模型在case 3 和case 4中得到的整体固含率εs,1相对实验值偏差分别为1.9%和3.9%，其余曳力模型给出的偏差相对较大。与收缩过程类似，TGS 曳力模型对动态膨胀过程预测较为准确。

表3 床层膨胀过程终止时的整体固含率实验值和模拟值Table 3 Experimental and simulated result of overall solids holdups after expansion process of liquid-solid fluidized bed

综合床层收缩与膨胀的4 个案例，TGS 模型对液固流化床动态特性的预测性能较优。曳力模型通常可以归纳为颗粒Reynolds 数和颗粒浓度的函数，TGS 曳力模型[32]有效范围为Res≤300 和0.1 ≤εs≤0.5，本文中其他曳力模型的适用条件涵盖层流到湍流区的颗粒Reynolds数及可能形成流化状态的全部颗粒浓度范围，因此5 个曳力模型均适用于本文所考察的4 个案例（颗粒Reynolds 数和颗粒浓度分别为25 ～55 和0.22 ～0.38）。而TGS 曳力模型预测性能较优的原因是因为该模型基于静止颗粒群绕流直接数值模拟结果，构建此类模型时无须考虑颗粒间碰撞的相互作用，精准表征了液固散式流化床内颗粒动力学特性；此外，对于通过实验构建曳力模型的传统方法，颗粒群中单颗粒受力难以直接测量，往往通过床层压降或沉降速度等间接信息来推算颗粒体系的平均曳力，而颗粒解析尺度的直接模拟在理论上可以精确地获取任一颗粒的受力信息。

3.2.3 升力模型对模拟结果影响 图9给出了升力模型对液固流化床膨胀特性的影响，考虑升力模型与否所给出的床层高度随时间分布近乎一致，因此所选取升力模型对动态膨胀特性模拟结果的影响较小。尽管升力等相间作用力在理论上已得到普遍承认，但由于多相流动体系的非线性和耦合性等特点，从颗粒实际受力中难以真正剥离出升力等相间力[18]，导致很多由实验结果所得曳力模型中已经包括了升力或其他相间力。另外，作用于颗粒的升力主要与剪切流动和自身旋转相关。模拟中采用了均匀来流的入口条件，导致流化床内液相剪切速率较小；相关研究[36]指出碰撞行为是引起颗粒旋转的主要原因，而液固散式体系的固有特征导致发生颗粒相互碰撞的概率较低。

4 结 论

图9 升力模型对床层膨胀特性的影响Fig.9 Effect of lift force model on expansion processes

以水-玻璃珠体系为具体研究对象，在对液固流态化稳态过程实验结果验证的基础上，考察了Wen-Yu、Gidaspow、Syamlal-O’Brien、Dallavalle 和TGS 5 个曳力模型以及升力模型对床层动态特性CFD模拟结果的影响行为，主要结论如下。

（1）稳定流化状态下整体固含率的实验测量结果与Richardson-Zaki 公式预测结果较为吻合，平均相对误差在5%以内。

（2）收缩过程中Syamlal-O’Brien 和TGS 曳力模型预测的响应时间较为准确，而TGS 曳力模型对整体固含率的预测精度较高；膨胀过程中TGS 模型对响应时间和整体固含率的预测优于其他曳力模型；Gibilaro 理论对液固流化床收缩过程具有良好的预测能力，但对膨胀过程的预测偏差较大。

（3）在本文考察范围内，可以确认TGS 曳力模型对液固流化床动态特性的预测性能最优，原因在于该模型基于静止颗粒群绕流的直接数值模拟而获得，符合液固体系的颗粒动力学特征。

（4）所考察升力模型对床层动态特性模拟结果影响较小，建立相间作用力模型时可予以适当忽略，其原因可能是基于实验测量的曳力模型往往已经包括了其他相间作用力。

符 号 说 明

CD——曳力系数

CL——升力系数

ds——颗粒粒径，mm

h——床层高度，mm

Res——颗粒Reynolds数

Tr——响应时间，s

u0,u1——操作速度，mm·s-1

β——动量交换系数，kg·m-3·s-1

ε——体积分数

μ——动力黏度，Pa·s

ρ——密度，kg·m-3

下角标

in——初始化状态

l——液相

s——固相

t——终端沉降状态

0——操作速度突变前的平衡状态

1——操作速度突变后的平衡状态