刍议三维物理问题的试题编制与分析策略
福建 郑行军
(作者单位:福建省福鼎市第一中学)
中学物理的三维问题是指物体运动过程的轨迹、位移、速度、电场强度等描述参量不以一维或二维坐标呈现,而是以三维空间的形式设置物理情境。立体空间建构的主要目的是通过转化或降维展开平面实现物理三维视图的直观可视处理,使物理问题能在低维度情况下进行观察、想象和分析。从知识结构来看,三维物理问题具有明显的数理融合特征,既要掌握物理模型相关必备知识,又要灵活应用数学方法进行转化处理;从考查能力看,主要考查学生空间想象能力和图像转化、处理能力,即应用数学知识处理物理问题的能力。因此三维物理问题的分析,对学生掌握数理融合的处理方法、拓展学生的思维能力、构建知识方法结构体系均有积极的意义。
一、三维轨迹问题试题编制与分析策略
1.三维轨迹模型
物体发生较为复杂的曲线运动时,一维或二维坐标无法完整描述轨迹信息,需要以三维空间的形式给予呈现,进而出现三维轨迹模型。必备知识一般涉及运动参量的降维分析或关联运动矢量的合成与分解。
2.三维轨迹模型的分析策略
轨迹模型的降维目的是呈现物体运动过程的真实路径,便于观察和分析运动规律和运动参量的几何关系,因此平面转化视角应基于轨迹的直观可视化描述,适当选择轨迹面的三视图或三维面展开图,若涉及复杂曲线运动的分解则需要做出两个分运动轨迹面的三视图。
【例1】如图1所示,一个惊险的转盘飞刀表演节目:一个勇敢者身体固定在快速旋转的竖直转盘上,另一个飞刀表演者不断地向转盘抛出飞刀。假设当转盘上勇敢者刚好处于水平位置时,飞刀沿着与竖直转盘平面夹角为θ方向水平抛出,速度大小为v。已知抛出位置在转盘平面的垂直中轴线上且离转盘中心距离为L,

图1
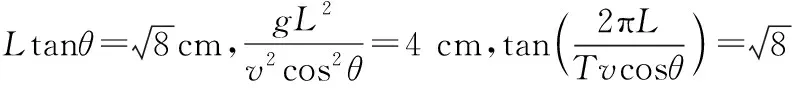

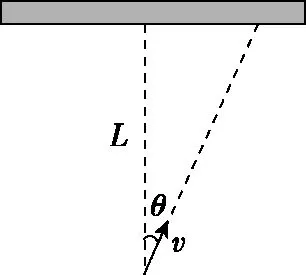
图2

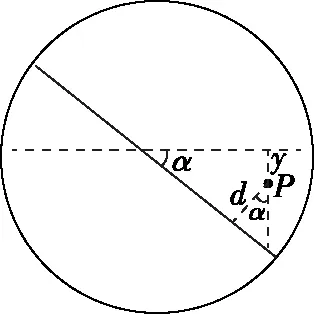
图3
联立得d=2 cm
【点评】小刀在空中运动轨迹与转盘运动结合产生三维的轨迹模型,因此要真实反映出小刀和转盘运动的运动参量关系,需进行降维转化,画出水平轨迹面和竖直轨迹面的平面视图,利用水平轨迹面找出水平位移和盘中心距离L的关系,利用竖直轨迹面确定盘面转过的角度、小刀击中的位置和竖直位移,通过竖直轨迹面呈现参量的几何关系,求出小刀与勇敢者的最近距离。本题分析过程轨迹的降维转化是至关重要的环节,它决定了运动参量能否直观的呈现,为后继运算研究提供便利参考。
【例2】如图4所示,圆台的上、下底面半径分别为r1=5 cm、r2=10 cm,母线AB长l=20 cm,一只小虫(可视为质点)从圆台母线AB的中点M以恒定的速率v=5 cm/s绕圆台侧面运动到B点(B在下底面),求:

图4
(1)小虫在圆台侧面运动的最短时间;
(2)在满足(1)条件下,上底圆周上的点与小虫的最短距离?
【解析】(1)画出圆台的侧面展开图(图5),将曲面转换为平面并还原成圆锥展开的扇形,且设扇形的圆心为O。

图5
由图得小虫运动的最短轨迹是直线段MB′,设OA=R,圆心角是θ,则由题意知,
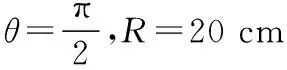
由几何关系得OM=30 cm,OB′=40 cm,△OMB′为直角三角形,根据勾股定理可得MB′=50 cm
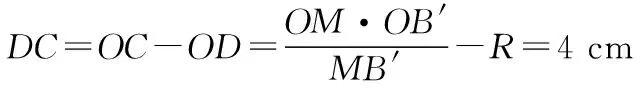
上底圆周上的点与小虫的最短距离是4 cm。
【点评】小虫沿圆台侧面不同的路径到达B点时间不同,曲面轨迹不好分析,可将圆台侧面沿母线展开转换成平面图,建构出直观的小虫运动平面轨迹,由轨迹图判断出直线段MB′最小,可求出最短时间,本题解题的关键在于会将曲面轨迹转为平面轨迹从而降低思考难度,综合圆台的几何性质构设相关几何变量的方程组而得解。
二、隐含性轨迹问题试题编制与分析策略
1.隐含性轨迹模型
在设计物理情境时对能反映物体运动特征的显性轨迹进行适当隐藏,或展示对分析过程无关紧要或有一定视觉障碍的轨迹视图。学生做题时需要在题设给予视图条件下进行合理的视图转换从而描绘出便于问题研究的有效图示,进而解决问题。
2.隐含性轨迹的分析策略
显性轨迹的隐藏或展示障碍性轨迹视图问题,需要根据条件或在原有展示视图的基础上,进行规范化视图描绘或转化,标准要依据题设要求而定,若关注轨迹则应转化成能真实反映轨迹路径的平面视图,若需反映物理量间的几何关系和运算则应转换成以物理量标准化展示为主,便于分析和研究的二维视图。
【例3】乒乓发球机的简化模型示意图如图6所示,发球机的机头相当于一个长l=20 cm的空心圆柱(内径比乒乓球的直径略大),水平固定在球台边缘O点上方H=45 cm处,可绕C轴在水平面内转动,从而改变球的落点。球台长为L=3 m位于球台中央的球网高h=25 cm,出球口离盛球容器底部的高度H0=50 cm,不考虑乒乓球的旋转、空气阻力和发球机轨道对球的阻力,已知重力加速度g取10 m/s2。

图6
(1)若发球机的机头不转动,且出球点在O点正上方,当发球机发出的球能过网且落在球台上,求发球机出球的速度大小范围;
(2)若发球机机头以ω=5 rad/s在水平方向发生顺时针(俯视)匀速转动,且出球时乒乓球相对机头的速度为9 m/s。求球点转到O点正上方时所发出球的最后落点位置,以O点为坐标原点,球台面中轴线为x轴在球台水平面建立直角坐标系,结果用xOy坐标系中的坐标值表示?


故发球机出球的速度大小范围为7.5 m/s≤v≤10 m/s
(2)发球机机头在水平方向发生顺时针(俯视)匀速转动,则乒乓球会在水平方向产生轨迹,画出水平面俯视图(图7),由图得机头转动的线速度为v3=ωl=5×0.2=1 m/s

图7
球出后做平抛运动,在xOy坐标系中,纵坐标为y=v3t2=0.3 m,横坐标为x=v4t2=2.7 m,最后落点位置P坐标为(2.7 m,0.3 m)。
【点评】题目条件只给予了乒乓球沿中轴线做平抛运动的轨迹,在第(2)小题中对乒乓球水平方向的运动轨迹进行隐含,需要根据题目条件及平抛轨迹的特征描绘出乒乓球在水平方向两个分运动的运动情况,由高度求出平抛运动的时间,将小球出来时的速度沿x和y方向分解,结合两个分速度求出两个分位移,确定球落点的位置坐标。
三、三维运动关联问题试题编制与分析策略
1.三维运动关联模型
系统内物体间发生相对运动时,运动参量(如位移、速度或加速度等)不共线或不共面,而在三维空间中形成相互关联模型。问题往往涉及相对运动(如相对速度)分析与运算。
2.三维运动关联问题的分析策略
三维运动关联模型主要研究运动参量之间的关联关系,重点聚焦相对运动的变化规律,因此思考方向应以运动参量(如位移、速度、加速度)的二维展示为目的,对题目条件的三维图像进行平面转换,以直观呈现便于分析运算的参量关联关系,结合三维结构体的几何特征求解。
【例4】如图8所示,长方体ABCD-A1B1C1D1的底面ABCD是正方形,正方形边长为L,点E在棱AA1上,BE⊥EB1。质点a以速度v沿直线轨迹从C1点向E点匀速运动同时,质点b以速度v沿侧面ABB1A1从B点向E点匀速运动,求:

图8
(1)以质点a为参考系,质点b的速度大小;
(2)若质点a、b恰好在E点相遇,两质点运动的时间?
【解析】(1)由正方体几何关系得,B1C1⊥平面ABB1A1,BE⊂平面ABB1A1,故B1C1⊥BE,又BE⊥EB1,故BE⊥平面EB1C1,BE⊥EC1,由条件可知质点a、b速度方向互相垂直。


图9

图10


四、三维位置关联问题试题编制与分析策略
1.三维位置关联模型
研究位置不共线或不共面,其承载于空间几何体上,呈现出三维的立体分布,试题一般结合几何体的结构特征和物理参量的空间分布规律进行编制和设计,物体的位置分布或运动路径与几何体的结构有一定的契合性。
2.三维位置关联模型的分析策略
位置在三维空间分布有一定复杂性,采用三视图平面转化有时无法直观呈现位置分布的几何关系,需要根据位置承载的空间几何体的结构特征,恰当添加截面图展示几何体的对称性,并与物理量分布规律有效结合,将三维问题转化为二维问题求解。
【例5】如图11所示,ABCD为一正四面体,A点固定一个电荷量为+Q的点电荷,B点固定一个电荷量为-Q的点电荷,E点为BC边的中点(图中未画出),以无穷远处电势为零。则下列说法中正确的是

图11
( )
A.C、D两点的电场强度相同
B.将一正电荷从C点移到E点,其电势能增加
C.将一点电荷沿直线从D点移到C点,电场力始终不做功
D.若在C点固定一电量为-Q的点电荷,则E点的电场强度指向A点
【解析】等量异种电荷的电场线分布情况如图12所示;

图12
如图13所示,过AB中点F做辅助线FC和FD,由正四面体的几何结构特征可知,AB⊥平面FCD,平面FCD为侧棱AB的中垂面,CD恰好在侧棱AB的中垂面上,结合由电场线的空间分布可知C、D两点的电场强度相同,A选项正确;E点靠近点电荷-Q,结合电场线空间分布,从C点到E点电势降低,将正电荷从C点移到E点,电场力做正功,其电势能减小;B选项错误;C、D两点的连线上的任意一点到A和B的距离相等,所以CD均在同一等势面上,则移动点电荷时电场力始终不做功,C选项正确;C点固定-Q的点电荷,则B、C两点电荷在E点的场强相互抵消,由电场强度的叠加原理和场强方向特征可知E点的电场强度方向由A点指向E点,D选项错误。

图13
【点评】本题场源位置和研究位置分布在正四面体上,几何关系不直观,需要构造正四面体的截面图(过CD做侧棱AB的中垂面)将三维位置关系转化为二维问题,结合正四体结构的对称性和等量异种电荷电场线的分布规律综合分析。
五、三维动力学问题试题编制与分析策略
1.三维动力学模型
物体处于静止或运动过程受到多个不共线或不共面的作用力而产生三维力学图示,物体图像展示可能为平面也可能为三维立体图像,模型主要聚集力学问题研究。
2.三维动力学模型的分析策略
三维动力学模型的降维目的是直观、规范呈现物体受力关系,便于观察和分析力的作用关系,利用图解法(如平行四边形定则、三角形定则)或解析法(如正交分解法)求解未知力学量。降维策略主要依据三视图平面转化将三维视图转换为几个标准的二维视图,平面转化视角应基于受力的直观可视化描述,具体分为以下几种类型:
(1)水平面的三维视图→正视图
(2)竖直面的三维视图→俯视图
(3)斜面的三维视图→侧视图
(4)若某一平面内受不共线的多个力作用→该平面的正视图
【例6】如图14所示,重为8 N的物块静止在倾角为30°的斜面上,若用平行于斜面且沿水平方向、大小为3 N的力F推物块时,物块刚好被推动。现施加平行于斜面的力F0推物块,使物块在斜面上做匀速运动,此时斜面体与物块间的摩擦力大小为Ff。设最大静摩擦力与滑动摩擦力大小相等,斜面始终保持静止,则
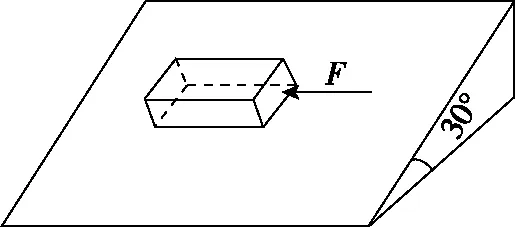
图14
( )
A.F0可能为0.5 N B.F0可能为5 N
C.Ff可能为3 N D.Ff可能为9 N


图15

图16
当推力F改为平行斜面的力F0作用时,斜面对滑块的最大静摩擦力Ffm=μFN仍为5 N,做出斜面的正俯视图如图17,依据平衡条件三个力始终可以构成三力首尾相接的闭合三角形,设静摩擦力达到最大值,根据三边关系得Ffm-F1≤F0≤Ffm+F1,即1 N≤F0≤9 N,BC选项正确。

图17
【点评】本题考查了共点力的平衡条件,难点在于物体受到的力不在同一个平面内,力的几何关系无法直观呈现,需要根据三维图示的特点分解成侧视图和斜面的正俯视图两个平面视图进行综合分析,在侧视图中将重力沿斜面和垂直斜面分解为两个分力,在斜面俯视图中利用力的矢量合成原理求出最大静摩擦力;施加平行于斜面的力F0推物块,F0方向可沿平行斜面任意变化,但与摩擦力和重力沿斜面的分力三个力仍然处于平衡状态,根据三力平衡条件的动态变化关系即可求出F0的可能取值。
六、结语


