LCL 型光伏并网逆变器全局鲁棒滑模变结构双闭环控制

刘吉宏， 刘鹏飞， 张树新， 王刘菲

（北京电子科技职业学院 机电工程学院， 北京 100176）

0 引言

光伏并网逆变器是光伏发电系统重要的能量转换设备，其控制性能直接影响到发电系统的电能质量[1]。 逆变器控制目标是滤除开关频率的谐波，保证输出电流的正弦度，实现对并网电流的精确跟踪，保证满足并网条件。

文献[2]针对LC 型滤波并网逆变器提出了一种自适应滑模全局鲁棒电压控制算法，该算法可以降低逆变系统输出电压的抖振、谐波畸变率和稳态跟踪误差，提高了逆变系统输出电压的动态调节能力及抵御滤波参数摄动的能力。 但LC 逆变系统并网时，输出电压被电网电压钳位，只有滤波电感对并网电流进行滤波，电容没有滤波效果，影响并网电流和基准电流的相位以及并网效果。 与LC 型滤波器相比，LCL 型滤波器成本低、损耗小、滤波效果好，能够减小并网电流的冲击作用。 但LCL 型滤波器为欠阻尼三阶系统，存在一个谐振点，容易发生谐振，影响系统稳定和增加控制难度。 常用的谐振尖峰抑制方法主要有无源阻尼法和有源阻尼法[3]，[4]。无源阻尼法无需传感器，无须改变控制算法，但在大功率场合中，电阻会消耗大量能量，需要加装散热装置，增加了设备投入[5]，[6]。 有源阻尼法不增加额外的电阻，不会给电路带来额外的能量损耗。 有源阻尼法可分为3 类：基于滤波器与电流调节器级联的有源阻尼、基于系统降阶的有源阻尼以及基于状态变量反馈的有源阻尼[7]。目前，并网逆变器系统中，普遍使用有源阻尼法中的电容电流反馈控制法， 该方法增加了系统阻尼，提高了谐振尖峰抑制能力[8]，[9]。 文献[10]提出了电容电流比例反馈和并网电流反馈的双闭环控制策略，该策略虽然具有较好的动、静态性能，但设计过程较复杂。为避免谐振，文献[11]对系统进行降阶处理，方便了控制算法的设计，但在前馈函数设计时没有考虑逆变器的延时， 影响了系统控制效果。 由于逆变器的输出电压须与电网钳位， 因此一般采用电流控制方案， 主要包括PI 控制、滞环控制、无差拍控制、比例谐振控制、准比例谐振控制、 重复控制和滑模变结构控制等[12]～[21]。 PI 控制易实现，在实际中应用较多，但对正弦量的跟踪存在误差，而且鲁棒性能也较差。滑模变结构控制的控制律更简单， 对系统的数学模型精确性要求不高，并具有响应速度快、动态性好等优点， 但所设计的滑模平面都是定常的滑模平面， 对滑模面以外的干扰和参数摄动不具有强鲁棒性。

本文采用双闭环的控制结构， 可以实现多目标的控制作用。内环引入滤波电容电流的比例-惯性反馈环节，抑制和提高带宽；外环电流控制器采用全局鲁棒滑模变结构控制，跟踪给定的正弦参考信号，同时对外界干扰和参数不确定性具有全局鲁棒性。 仿真结果验证了本文方法在跟踪效果和抗干扰方面优于常规的PI 控制算法。

1 LCL 型滤波光伏并网逆变器数学模型

三相LCL 型光伏并网逆变器拓扑结构如图1所示。图中：Vdc为直流侧电压；Cd为直流侧电容，维持母线电压恒定；S1～S6为构成全桥逆变电路的6 个开关管；L1，L2，C 分别为LCL 滤波器的滤波电感及滤波电容；R1，R2为LCL 滤波电感的寄生电阻；i1为逆变器逆变侧的电流；i2为逆变器并网侧电流；Vg为电网电压。

假定电网电压三相波形对称，并且没有畸变。通过坐标变换，三相电路可转换为两相对称电路，取LCL 滤波器的单相等效电路进行研究，单相电路拓扑结构如图2 所示。

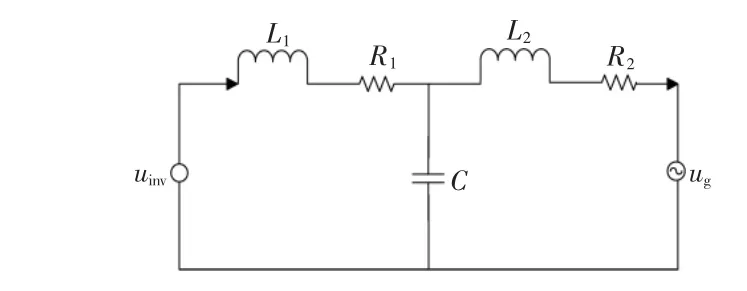
图2 单相电路拓扑结构Fig.2 Topological structure of single-phase circuit

取LCL 型滤波器为被控对象，滤波器并网电流i2为被控量，电网电压ug为扰动量。 由图2 可得到单相LCL 滤波器结构框图，如图3 所示。

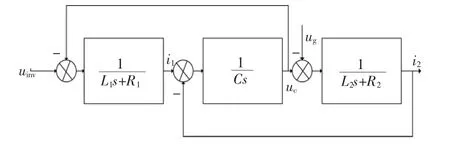
图3 单相LCL 滤波器结构框图Fig.3 Block diagram of single-phase LCL filter

不考虑寄生电阻，根据梅逊公式和图3 可得：逆变器输出电压到入网电流i2的传递函数和电网电压扰动ug到入网电流i2的传递函数分别为

2 双闭环控制系统的设计

2.1 LCL 型滤波器谐峰抑制

由式（1）得到图3 的等效框图，如图4 所示。

图4 系统等效框图Fig.4 The system equivalent block diagram

由于电容电流反馈简单易于实现， 可采用该有源阻尼方式抑制尖峰谐振。 采用滤波电容电流比例反馈的有源阻尼方法，可以提高带宽，同时可等效于在滤波电容上并联阻尼电阻， 而并联电阻的阻尼效果不如在电容支路上串联电阻。 为达到与在滤波电容支路串联电阻的等效效果， 在电容电流反馈回路中加入惯性环节， 提高了系统的阻尼，同时具有微分效果。反馈通道上的传递函数为

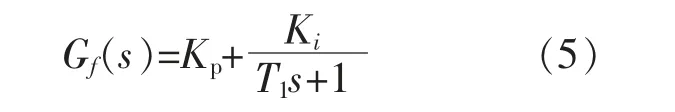
式中：T1为惯性环节时间常数；Ki为惯性环节增益；Kp为比例增益。

引入电容电流比例-惯性反馈后， 逆变器输出电压到入网电流的传递函数为

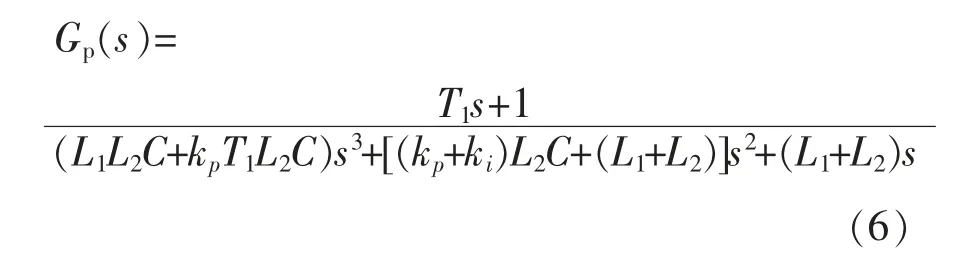
2.2 基于全局鲁棒滑模控制的电流控制器设计

结合普通线性滑动模态与快速Terminal 滑动模态的优点，通过设计合适的控制律，使系统在有限的时间内由滑动模态的任意初态渐进收敛到平衡零点。 利用Terminal 吸引子改善趋向平衡态的收敛速度，使得系统状态无论在远离平衡点，还是接近平衡点时，都具有快速收敛的速度。

由式（6）得到系统的能控标准型为

3 仿真及结果分析

外环分别采用PI 控制算法和全局鲁棒滑模变结构控制算法， 内环采用基于电容电流比例-惯性反馈的有源阻尼算法，进行对比仿真研究。为便于比较， 对实验结果作了归一化处理。 仿真条件：电网电压为220 V，直流侧电压为360 V，开关频率为10 kHz。 LCL 滤波器参数：L1=1.066 mH，L2=1.022 mH，C=10 μF，R1=R2=0.005 Ω。

3.1 稳态和动态性能分析

理想电网条件下， 入网电流给定值为标准正弦函数，对比仿真实验结果如图5 所示。

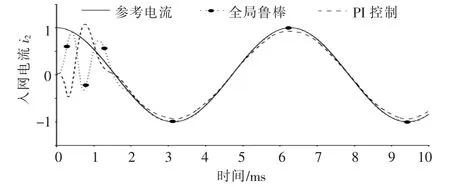
图5 入网电流性能对比曲线Fig.5 Comparison curve of state performance of grid current

由图5 可知， 相同设计参数下，PI 控制算法存在跟踪误差， 而全局鲁棒滑模变结构算法具有较好的跟踪效果，能够较快地跟踪电流给定值。

3.2 鲁棒性能分析

通过改变网侧电感的方式模拟系统参数的摄动。将网侧电感值由1.022 mH 变为1.5 mH 后，实验曲线如图6 所示。

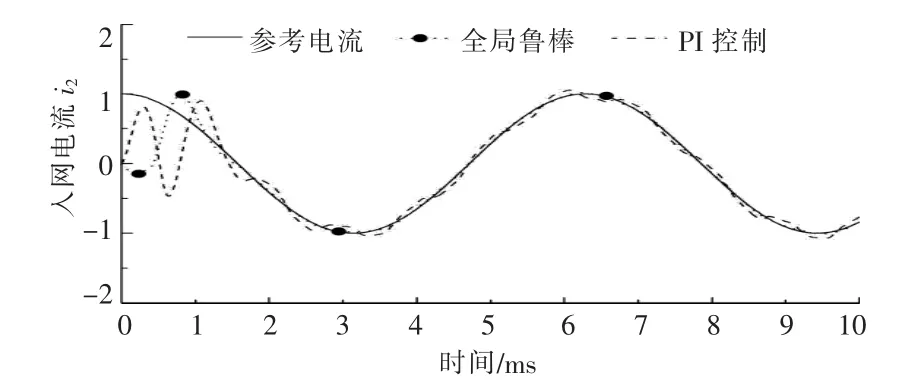
图6 参数摄动时入网电流对比曲线Fig.6 Comparison curve of grid current under parameter perturbations

由图6 可以看出，当系统参数改变时，本文方法对改变不敏感，表现出较强的鲁棒性。这是因为系统参数的摄动可被视为外界扰动， 全局滑模控制是通过设计一种动态非线性滑模面来实现的，消除了滑模控制到达的运动阶段， 使系统的状态开始就位于滑模面上， 在响应的全过程对外界扰动具有强鲁棒性，实验结果验证了这一点。

3.3 并网电流抗谐振能力分析

为验证系统的谐振抑制能力， 在电网电压中加入13 843 rad/s 的微量扰动信号，对比曲线如图7 所示。

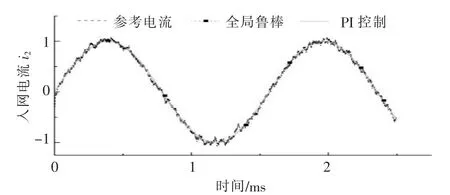
图7 加入微量扰动时入网电流对比曲线Fig.7 Comparison curve of grid current under the micro-perturbations

由图7 可以看出，与PI 控制算法相比，采用本文的控制策略，系统的入网电流更加光滑，谐振峰值得到了很好地抑制。

图8，9 分别为两种控制策略入网电流的谐波频谱分析图。

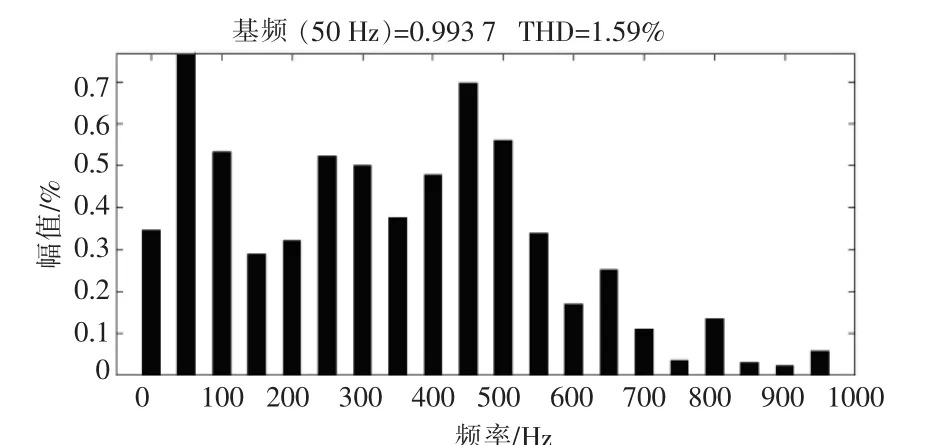
图8 全局鲁棒滑模控制时入网电流谐波分析Fig.8 Harmonic analysis of grid current in GSMC

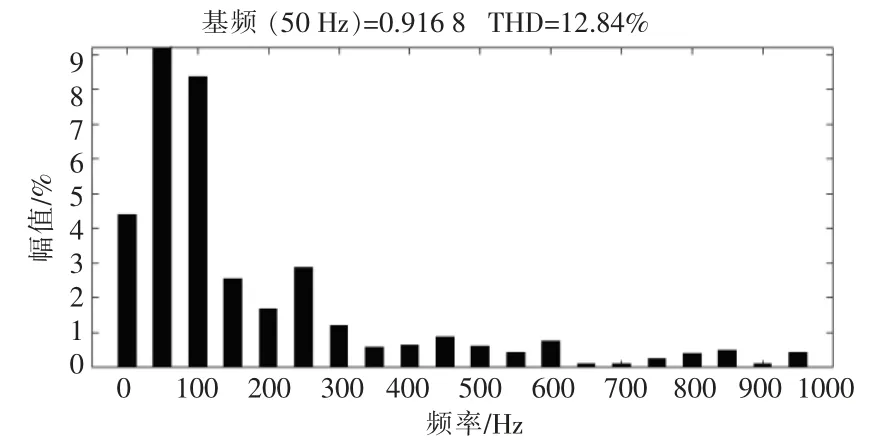
图9 PI 控制时入网电流谐波分析Fig.9 Harmonic analysis of grid current in PI

由图8，9 可以看出，基于全局鲁棒滑模变结构的控制算法的总谐波失真 （Total Harmonic Distortion，THD）仅为1.59%，明显低于常规PI 控制算法的THD 值12.84%。 实验结果验证了本文的控制策略在谐波抑制性能方面有明显提高。

4 结论

LCL 型光伏并网逆变器是一个三阶系统，在谐振频率处存在幅值增益尖峰，稳定裕度小。本文采用有源阻尼法， 通过电容电流反馈增加系统的阻尼，构成控制系统的内环，有效地抑制了谐振峰值。为了更好地跟踪参考信号，有效地抑制电网电压的干扰和模型参数摄动， 外环的电流控制器采用全局鲁棒滑模变结构控制算法， 使系统的状态始终位于滑模面上，保证控制的全局鲁棒性。仿真结果验证了控制方法的有效性。