不同布置方式下真空管太阳能集热器的热性能以及入射角修正系数的对比试验研究
王恩宇, 孟 颖, 唐世乾, 甄金玉, 郭 强
(河北工业大学 能源与环境工程学院, 天津 300401)
0 引言
太阳能集热器是太阳能热利用系统的核心部件。 太阳能集热器的集热性能对整个系统的各项性能具有重要影响[1]~[4]。太阳能集热器主要包括真空管太阳能集热器和平板太阳能集热器。 与平板太阳能集热器相比,真空管太阳能集热器在很大的温度范围内具有更高的集热效率, 因此,国内外学者对真空管太阳能集热器的热性能进行了大 量研究[5]~[7]。
张涛通过数值模拟研究发现,反射板、倾斜角度和太阳辐照度等参数会对真空管太阳能热水器的传热性能产生影响[8]。 Nie 通过研究发现,当太阳辐照度较低时,U 型真空管太阳能集热器的集热效率对其内工质的质量流量以及太阳辐照度变化的敏感性较高[9]。 Gao 通过研究发现,当环境温度较低时,真空管太阳能集热器的热损失系数对其瞬时集热效率影响较大[10]。 宋爱国提出了入射角乘积因子, 并使用数值计算的方法得出,斜置真空管集热器单管的入射角乘积因子大于横置真空管集热器单管的入射角乘积因子[11]。Tang 基于遮挡系数和投影入射角得出,竖置真空管太阳能集热器接收到的太阳辐射能多于横置真空管太阳能集热器, 且真空管集热器的安装角度应小于当地纬度[12]。
综上可知,目前,学者们主要针对某一布置方式下真空管太阳能集热器的热性能进行研究,对不同布置方式下真空管太阳能集热器的热性能进行对比分析的情况较少。 本文分析了2 种布置方式(横向、竖向布置)条件下,真空管太阳能集热器的热性能。 由于真空管太阳能集热器的热性能会受到入射角的影响,因此,测试该集热器的热性能时,须要考虑入射角修正系数。 当入射角相同时,不同布置方式下, 真空管太阳能集热器内光线的传输路径不同,因此,光学性能存在差异。 本文主要研究不同布置方式下, 真空管太阳能集热器的热性能和入射角修正系数。
1 试验参数和试验装置
1.1 试验参数
1.1.1 太阳能集热器瞬时集热效率
准稳态条件下, 真空管太阳能集热器的瞬时集热效率η 为准稳态条件下, 该集热器获得的有用功率与其表面上接收到的太阳辐照度之间的比值。 真空管太阳能集热器所获得的有用功率Q 的计算式为

式中:m 为真空管太阳能集热器内工质的质量流量,kg/s;Cf为真空管太阳能集热器内工质的比热容,kJ/(kg·℃);ΔT 为真空管太阳能集热器进、出口处的温度差,℃。
本文中的真空管太阳能集热器铺设在斜屋顶上,斜屋顶对太阳光具有漫反射作用。 斜屋顶面的材料为铝板。 本文基于真空管太阳能集热器的轮廓采光面积Ac, 来确定该集热器的集热面积。Ac的计算式为

式中:η0c为当T*=0 时, 真空管太阳能集热器的瞬时集热效率;Uc为基于Ti*的真空管太阳能集热器的总热损系数,W/(m2·℃);a1c,a2c均为拟合ηc与Ti*函数关系时得到的系数。
对于真空管太阳能集热器瞬时集热效率的计算式,可以利用最小二乘法拟合得出,进而得出式中各个系数。
1.1.2 入射角修正系数
真空管太阳能集热器的瞬时集热效率会随着太阳光线入射角的变化而变化,因此,须要引入入射角修正系数来评价真空管太阳能集热器的热性能。入射角修正系数Kθ为入射角等于θ 时的真空管太阳能集热器瞬时集热效率η0,θ与垂直入射时的真空管太阳能集热器瞬时集热效率η0,n之比。由于试验要求, 真空管太阳能集热器进口温度非常接近环境温度,因此,ti-ta≈0,则入射角修正系数Kθ与真空管太阳能集热器集热效率之间的关系式为

η0,θ,η0,n均 由 采 集 的 热 量 数 据 计 算 得 到,其中,η0,n可由集热效率曲线在y 轴上的截距得到。将入射角修正系数Kθ引入瞬时集热效率计算式[式(5),(6)],可得到如下计算式。
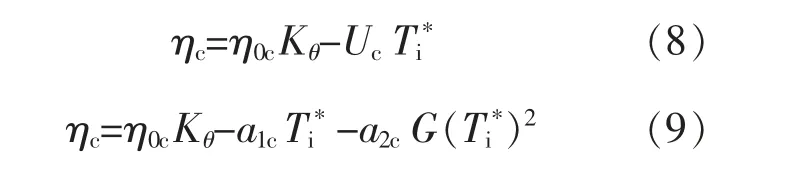
试验过程中,测定参数的允许偏差见表1[13]。

表1 试验过程中,测量参数的允许偏离Table 1 Allowable deviation range of measurement parameters during the test period
1.2 试验设备
1.2.1 试验测试系统
试验测试系统位于天津市河北工业大学节能楼楼顶(39.22°N,117.13°E)。 楼顶为倾斜面,倾角为30°。根据真空管布置方式的不同,将试验测试系统分为2 组分体式集热器试验台。 各试验台上真空管太阳能集热器的布置形式示意图见图1。
试验测试系统中的2 组真空管太阳能集热器均由24 支全玻璃真空管组成。 每支全玻璃真空管的几何尺寸均为Φ47 mm×1 500 mm,管间距均为26.6 mm, 每支全玻璃真空管的容积均为0.002 6 m3。 连接管道的保温层为岩棉,厚度为50 mm,外包裹镀锌铁皮。 真空管太阳能集热器采用并联的连接形式,朝向为南偏东21°,并且安装倾角可以在30~70°内进行调节。
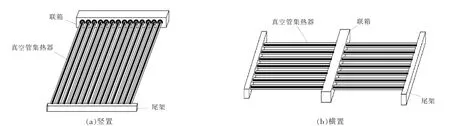
图1 真空管太阳能集热器布置形式的示意图Fig.1 Schematic diagram of evacuated tube solar collector layout form
试验测试系统的原理图如图2 所示。

图2 试验测试系统原理图Fig.2 Test system schematic
试验测试系统的实物图如图3 所示。

图3 试验测试系统实物图Fig.3 Test system physical map
1.2.2 测试设备
①硬件部分
本文利用TINEL-QX5 型气象环境自动观测站测得气象数据; 利用CRL-H 型户用超声热量表测得真空管太阳能集热器传热工质的进、出口温度,瞬时流量,累计流量和累计热量。CRL-H 型户用超声热量表中的温度传感器安装在每组真空管太阳能集热器出口的150 mm 处, 型号为Pt1000,测量值为0~95 ℃,最小配对温度误差为±0.1 ℃;流量测量值为0.06~12 m3/h。 该热量表安装在集热器进水管段,其前、后分别保留了长度为1,0.3 m 的直管段, 以保证流量测量结果的准确性。
②软件部分
本试验台利用西门子wincc 控制软件,将SIEMENS S7-200 与PC 端相连接,CRL-H 型户用超声热量表采用MODBUS 通讯协议, 并通过PLC 的CPU 总线连接到局域网,然后再利用互联网与PC 端相连接,将数据储存到电脑中。
2 试验概况
2.1 不同布置形式下瞬时集热效率对比研究
为了获取不同布置形式下, 真空管太阳能集热器的准稳态瞬时集热效率, 本文分别在晴天和少云的气象条件下进行试验, 并获取更大范围的归一化温差。 试验时间为9 月5 日-20 日的9:00-15:30,设定真空管太阳能集热器的安装倾角为30°,工质流量为208 kg/h。
真空管太阳能集热器集热效率测试试验的相关参数如表2 所示。
由于真空管太阳能集热器的瞬时集热效率曲线须在跟踪试验台上测得,因此,在选取试验数据时, 选择入射角接近于垂直入射的工况进行准稳态瞬时集热效率的研究。 在入射角小于10°的工况下,进行公式拟合。 根据GB/T 4271-2007 以及拟合条件的紧密程度来选择一次或二次曲线。 本试验对不同布置形式下的试验数据进行线性拟合,横置、竖置真空管太阳能集热器集热效率ηh,ηs的拟合表达式分别为

由式(10),(11)可得,横置真空管太阳能集热器 的 总热 损 失 系 数 为3.19 W/(m2·℃),竖 置 真空管太阳能集热器的总热损失系数为3.80 W/(m2·℃),这表明2 种布置形式下,真空管太阳能集热器的总热损失系数相接近。 由此可知,总热损失系数与真空管太阳能集热器的布置方式关系不大。
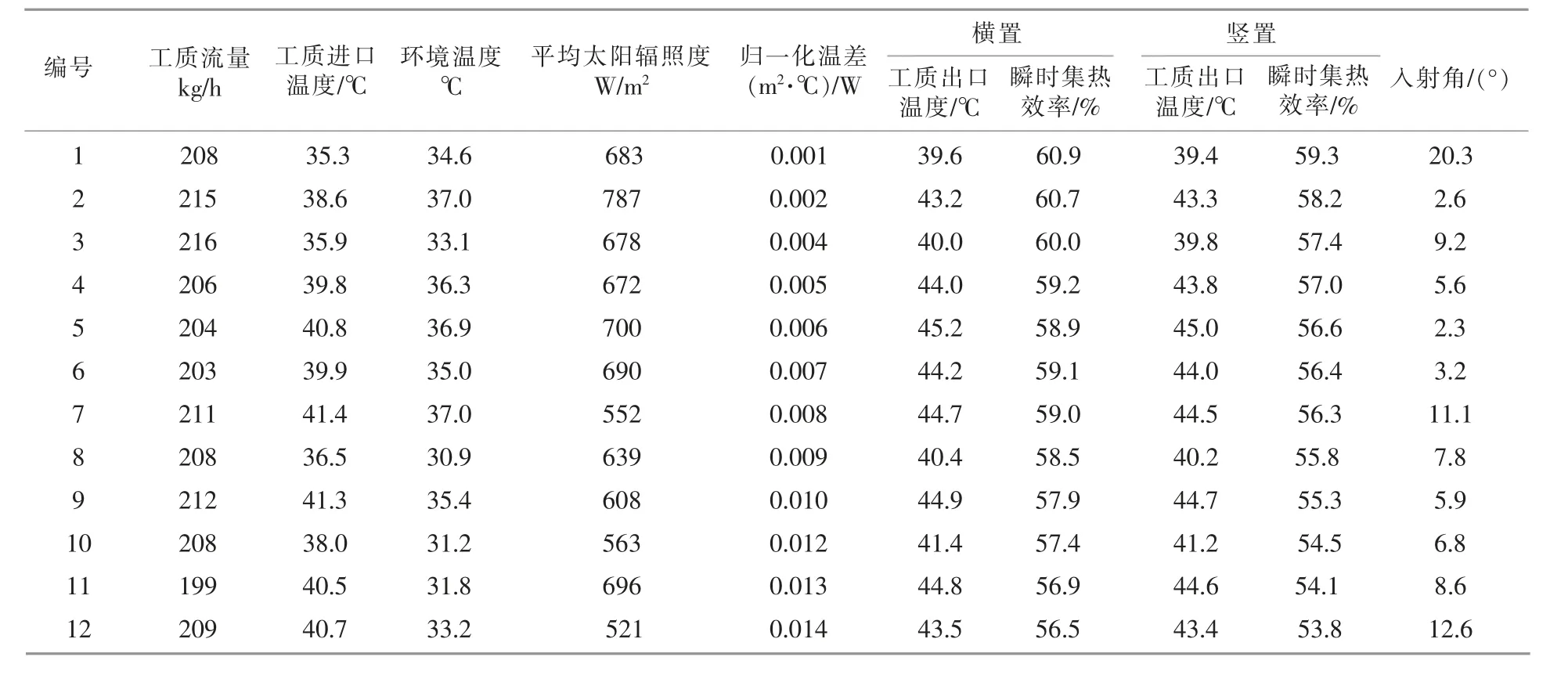
表2 真空管太阳能集热器集热效率测试试验的相关参数Table 2 Relevant parameters of evacuated tube solar collector efficiency test
对试验数据进行二次拟合可得,横置、竖置真空管太阳能集热器集热效率ηh,ηs的二次拟合表达式分别为
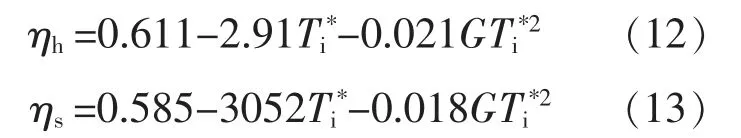
结合式(6)可知,若a2c为负数,则不应该选用真空管太阳能集热器集热效率的二次拟合表达式。根据式(12),(13)可知,2 种布置方式下,a2c的计算结果均不是负数,因此,对于这2 种布置方式下的真空管太阳能集热器,均应选择集热效率的二次拟合表达式。
不同布置形式的真空管太阳能集热器瞬时集热效率随时间的变化情况如图4 所示。
由图4 可知,横置真空管太阳能集热器的瞬时集热效率随时间的增加呈现出先升高后降低的变化趋势,12:00 左右,瞬时集热效率最高;竖置真空管太阳能集热器的瞬时集热效率随时间呈现出先降低后升高的变化趋势。 产生上述不同变化趋势的原因在于不同布置形式下,真空管太阳能集热器的入射角修正系数存在差异。
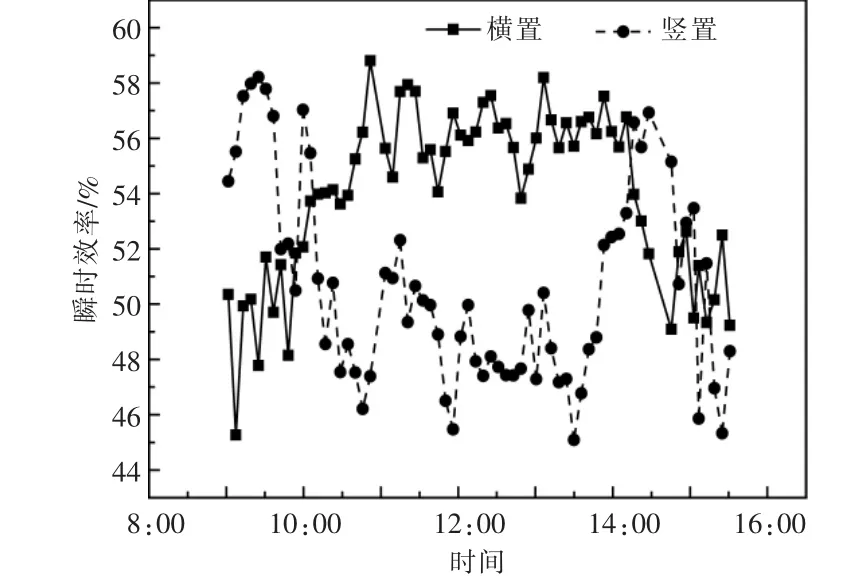
图4 不同布置形式的真空管太阳能集热器的瞬时集热效率随时间的变化情况Fig.4 Curve of instantaneous efficiency of evacuated tube solar collector with different layouts over time
2.2 不同布置形式下入射角修正系数对比研究
根据GB/T 4271-2007 规定,普通太阳能集热器只需要4 个入射角,即0,30,45,60°。本试验为了保证测量结果的准确性, 增加了入射角为15,75°的试验工况。 对于每个数据点,工质进口温度应该尽量接近环境温度(两者差值应在±1 ℃以内)。 试验测试时间为2019 年7 月8-10 日。
为了得到所需的入射角, 须要在一定太阳时角下,调节真空管太阳能集热器的安装倾角。真空管太阳能集热器安装倾角的调节步骤: ①根据试验时期确定日序数,计算试验时期的太阳赤纬角;②初步假设真空管太阳能集热器的安装倾角,然后,按照国际标准的相关规定,确定入射角、太阳时角,进而确定试验测试时间;③根据计算结果调节真空管太阳能集热器的安装倾角。
试验过程中,工质的流量设定为208 kg/h,并根据真空管太阳能集热器安装倾角的计算结果调节该集热器的实际安装角度。 试验周期包括30 min 的预备期和30 min 的稳态测量期。 由于工质进口温度与环境温度相接近,因此,可以认为tita≈0。 然后,根据式(7)计算得到真空管太阳能集热器的入射角修正系数Kθ。
不同布置形式真空管太阳能集热器的入射角修正系数计算结果如表3 所示。表中:θ 为太阳光线入射角(简称为入射角);Kθ,W-E,Kθ,N-S分别为横置、竖置真空管太阳能集热器的入射角修正系数。
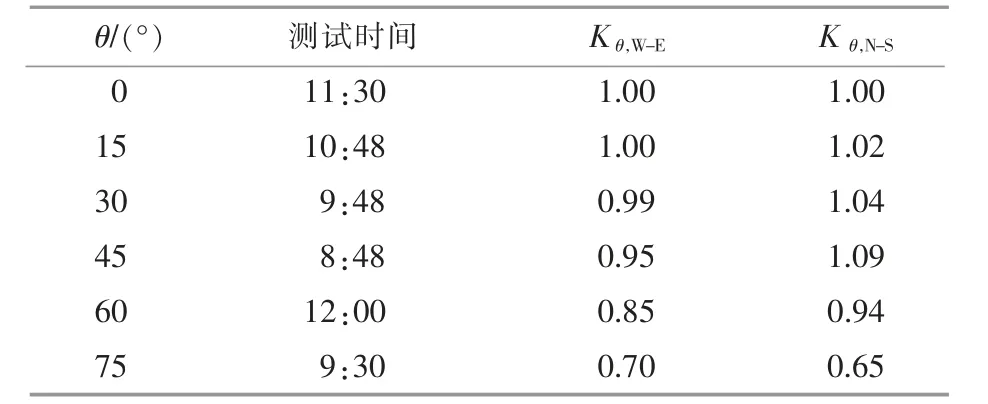
表3 不同布置形式的真空管太阳能集热器的入射角修正系数计算结果Table 3 Calculation results of incident angle modifier for evacuated tube solar collectors with different layouts
本文根据GB/T 4271-2007 的要求,将入射角修正系数计算结果绘制在Kθ-θ 图上, 得到真空管太阳能集热器入射角修正系数随入射角的变化情况,如图5 所示。
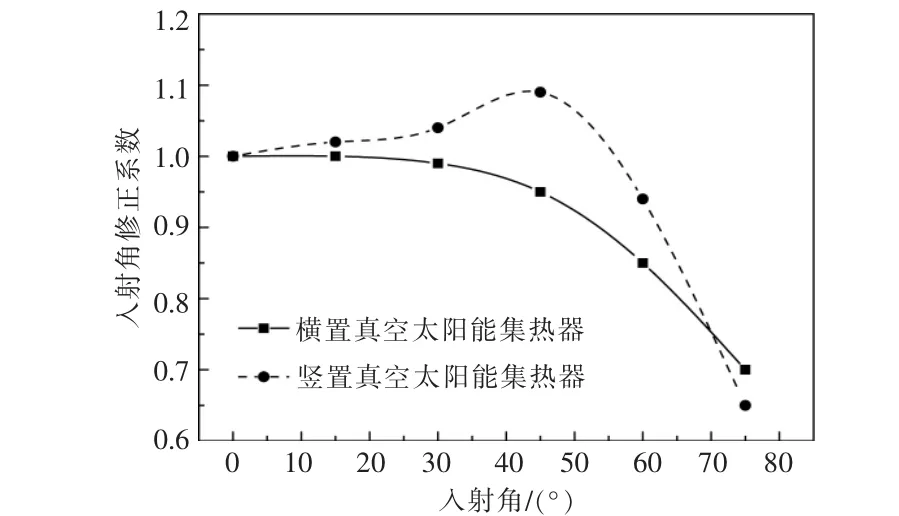
图5 不同布置形式的真空管太阳能集热器的入射角修正系数随入射角的变化情况Fig.5 Variations of the incident angle modifier of evacuated tube solar collectors of different layouts as a function incident angle
由图5 可知,对于竖置真空管太能集热器,当入射角由0°逐渐增大至45°时,Kθ,N-S逐渐增大,当入射角为45°时,Kθ,N-S达到最大值 (1.09);当入 射 角 由45 °逐 渐 增 大 至75 °时,Kθ,N-S逐 渐 减小,其中,当入射角为15~58°时,Kθ,N-S大于1;当入射角大于58°时,Kθ,N-S小于1。 对于横置真空管太阳能集热器,当入射角由0°逐渐增大至75°时,Kθ,W-E逐渐减小。 由图5 还可看出,当入射角为0~15°时, 这2 种布置形式的真空管太阳能集热器的入射角修正系数均变化较小,约为1。
2 种布置形式的真空管太阳能集热器的入射角修正系数与自身接收到的太阳辐射有关。太阳辐射包括直射辐射、散射辐射和反射辐射。 对于竖置真空管太阳能集热器,当入射角为0 °时,反射辐射最小,随着入射角逐渐增大,直射光线和部分散射光线透过集热管间隙照射在漫反射板上并发生反射,反射光线被其他真空管太阳能集热器吸收; 对于横置真空管太阳能集热器,部分直射光线与其平行,光线照射到漫反射板上直接反射至空气中,并未被集热器吸收。 2 种布置形式的真空管太阳能集热器的反射辐射示意图如图6 所示。
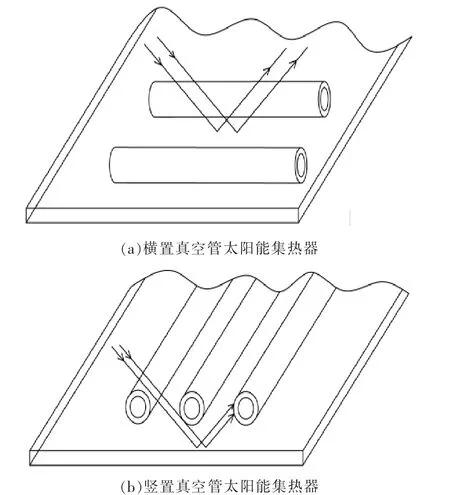
图6 两种布置形式的真空管太阳能集热器的反射辐射示意图Fig.6 Schematic of reflected radiation of two types of evacuated tube solar collectors
综上可知,当入射角小于45°时,竖置真空管太阳能集热器入射角修正系数随着入射角的增加而增加, 横置真空管太阳能集热器的入射角修正系数随着入射角的增大而减小。 根据式(7)可得:对于竖置真空管太阳能集热器, 当太阳光线倾斜入射时, 该集热器的瞬时集热效率高于太阳光线垂直入射的工况;对于横置真空管太阳能集热器,当太阳光线倾斜入射时, 该集热器的瞬时集热效率低于太阳光线垂直入射的工况,因此,竖置真空管太阳能集热器的瞬时集热效率随着时间的增加呈现出先减小后增大的变化趋势, 横置真空管太阳能集热器的瞬时集热效率随着时间的增加呈现出先增大后减小的变化趋势, 这与图4 的变化趋势相一致。
当入射角由45°增大至75°时, 相邻集热管之间产生遮挡[12]。 当光线在集热管横断面上的投影与集热器法线的夹角大于临界投影入射角Ω0时,相邻集热管之间会发生遮挡,这样会导致竖置真空管太阳能集热器接收到的太阳辐射中不存在直射光线产生的反射辐射, 同时直射辐射骤然下降。 因此,入射角由45°增大至75°时,竖置真空管太阳能集热器入射角修正系数的下降速度比横置真空管太阳能集热器快。 Ω0的示意图见图7。
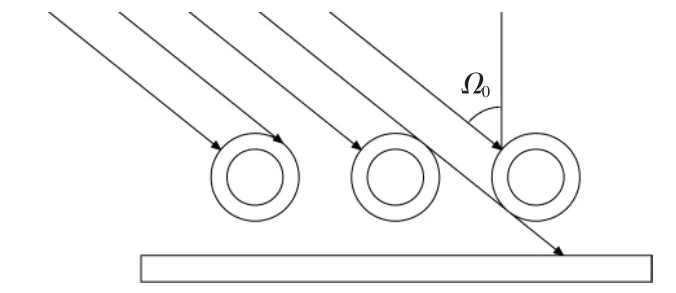
图7 临界投影入射角示意图Fig.7 Critical projection incidence angle
根据GB/T 4271-2007 的规定,当入射角不大于10°时, 不必使用入射角修正系数对真空管太阳能集热器接收到的太阳能进行修正。 根据表3和图5 可得出不同入射角条件下的真空管太阳能集热器入射角修正系数。 为了验证增大入射角修正系数时, 利用瞬时集热效率评价真空管太阳能集热器热性能的准确性也随之增大, 本文将试验所得的Kθ,W-E,Kθ,W-S代入式(12),(13),得到横置、竖置真空管太阳能集热器瞬时集热效率修正公式分别为

将入射角大于10°时, 各参数的测量结果代入式(14),(15),可得到不同入射角修正系数条件下的真空管太阳能集热器瞬时集热效率,并将有、无入射角修正系数的试验结果的计算误差进行对比,见表4。 由表4 可知,将横置、竖置真空管太阳能集热器入射角大于10°的归一化温差以及太阳辐照度(表2)代入有、无入射角修正系数的瞬时集热效率的拟合公式发现, 对于有入射角修正系数的真空管太阳能集热器, 其瞬时集热效率拟合公式计算结果的准确性较好,但是优势并不明显。这是由于本文试验过程中的入射角较小, 当横置真空管太阳能集热器的入射角小于30°, 竖置真空管太阳能集热器的入射角约为15°时, 二者的修正系数接近于1,因此,上述情况下,可以忽略对真空管太阳能集热器的修正。

表4 有、无入射角修正系数的试验结果的计算误差Table 4 Error analysis of correction coefficient with or without incident angle
3 结论
①当真空管太阳能集热器布置在倾角为30°的倾斜面上时, 横置真空管太阳能集热器瞬时集热效率随时间的增加呈现出先升高后降低的变化趋势, 竖置真空管太阳能集热器瞬时集热效率随时间的增加呈现出先降低后升高的变化趋势,这与不同布置形式下, 真空管太阳能集热器入射角修正系数的差异相关。
②当入射角由0°逐渐增大至75°时,横置真空管太阳能集热器的入射角修正系数逐渐减小。对于竖置真空管太阳能集热器,当入射角由0°逐渐增大至45°时, 该集热器的入射角修正系数逐渐增大;当入射角由45°逐渐增大至75°时,该集热器的入射角修正系数逐渐减小。
③当横置真空管太阳能集热器入射角大于30°, 竖置真空管太阳能集热器入射角大于15°时, 将入射角修正系数引入瞬时集热效率拟合公式后,可以明显提高热性能评价的准确性。

