基于遗传算法的区域防空部署应用

潘永强 吴凯 董诗音 姜鸿儒 雷建杰

防空部署是对兵力作战效能的有效利用,部署的好坏程度将直接影响整个防空作战结果,在当前复杂多变的敌情和有限兵力资源情况,如何将防空部署效能做到更优是防空作战研究的重点与难点[1−3],目前,国内防空部署的研究成果大致如下几点,一是根据部署方案的相关特征,建立并计算部署方案的贴近度,从而得到部署方案的改进策略[4],此方法需要融入大量人为评价因素,部署优化程度有待提高;二是在防空部署权重不确定时采用多属性决策方法(MAMD),考虑不同因素权重,使得计算得到的防空部署方案更加科学可靠[5−7],但由于考虑的因素较多且差异性较大,该方法实际应用过程较为复杂;三是通过层次分析法建立防空部署评价指标体系,采用正态云拟合算法选出最优防空部署方案[8],该方法实现了定性到定量的合理转化,在单个武器系统防空部署优化计算上效率较高,但对于多武器系统防空部署的优化计算难度则因考虑因素的复杂程度增大而增大;四是考虑来袭目标和本武器系统杀伤性能等要素,建立仿真评估系统,模拟仿真防空作战过程,优化部署[9−11],此方法仅考虑了单武器系统防空部署仿真,暂未对多武器系统的防空部署进行仿真;五是通过建立多目标防空部署模型,得到考虑多目标因素的目标函数,采用遗传算法求解防空部署优化模型[12],遗传算法能很好地解决多目标优化收敛问题,是一种简单有效处理防空部署优化问题的实用方法,但目前为止防空部署优化模型仅考虑了单点防空部署,而并未考虑到整个防空区域的区域性部署效能.

通过以上研究发现,采用遗传算法优化防空部署方案不失为一个好方法,2003年,国内就已经尝试并探索遗传算法在防空兵火力分配上的应用[13],在建立遗传算法模型的基础上仿真运算,得到具有一定参考价值的分配方案,在战役方向兵力优化分配方面,建立防空部署分配的数学规划模型,改进遗传算法[14],并最终得到单个防空武器在对抗典型目标下的部署方案,而未考虑到多武器系统防空部署优化问题,且涉及到多种武器混合部署下的优化模型较为复杂[15],是防空部署优化研究的重点.

从防空部署区域的角度来考虑,区域性防空部署更能有效地反映整个防空部署的性能,将更有效的作战资源部署在更加需要保卫的要地中心,同时能够兼顾保护在防空区域内其他非重点保护的要地,做到合理利用武器资源、合理部署.所以,如何做到在考虑多目标多类型兵力资源的基础上,有效利用对保卫要地的区域性管理,得到最优化的防空部署方案,是目前防空部署研究上的难点,本文就防空部署问题进行了较为深入的分析,提出从单点要地防空转为区域性要地防空,建立了防空区域的设计模型,并设计防空区域的兵力部署数学模型,将遗传算法应用于区域防空部署模型的求解,得到了较为理想的结果.

1 区域防空部署流程

随着目前武器装备升级换代速度的加快,现有武器装备保卫能力越来越强,保卫覆盖范围也越来越大,采用一个防空武器系统仅保卫单个防空要地的方式已与目前防空武器的高速发展相矛盾,故本文在要地单点防空部署的基础上,提出区域化的防空部署,使得一个防空武器系统可以同时保卫多个防空要地,减少资源使用成本,实现更高效的防空部署,并基于区域化防空的特点,建立区域防空部署模型,采用遗传算法求解得出最优的区域防空部署方案.

本文对区域防空部署应用研究的流程如下:

1)要地单点防空区域化.

2)建立区域防空最优部署目标函数.

3)基于遗传算法解算区域防空最优部署方案.

4)区域防空部署遗传算法模型优化分析.

流程图如图1所示.

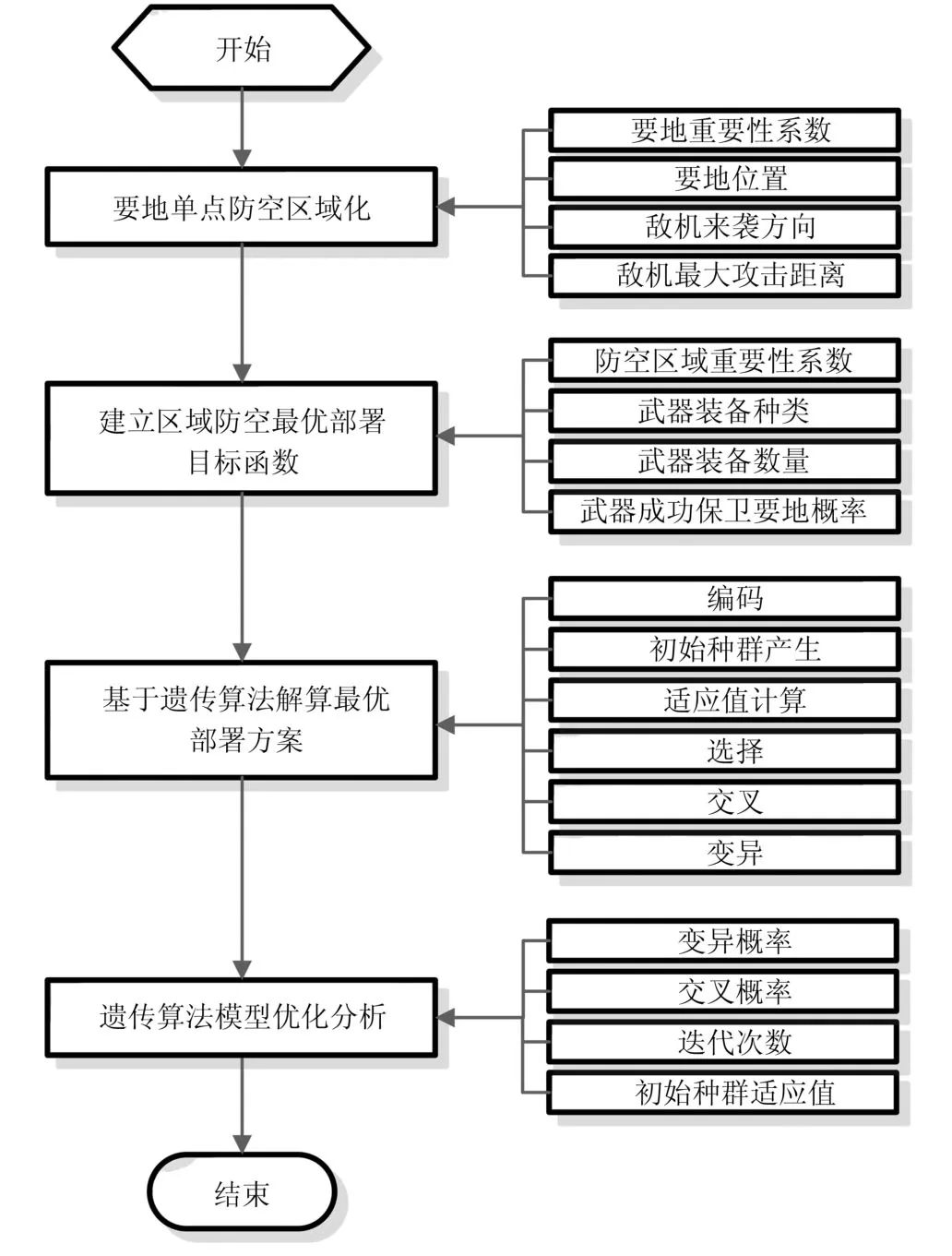
图1 基于遗传算法的区域防空部署流程Fig.1 Regional air defense deployment process based on genetic algorithm

2 区域防空部署模型

2.1 要地单点防空区域化

防空部署,主要是为了最大化发挥各类防空武器的性能,以更高的效能来保卫我方要地[16],为了建立区域化防空部署的数学模型,对部署条件抽象描述如下:

设防空部署可用的武器有m种,且第i(i=1,2,···,m)种武器有ni套,要地个数为r,要地的重要性系数为wj(j=1,2,···,r),保卫性系数为eij.wj表示j要地的重要程度,eij表示i武器成功保卫j要地的概率.

在防空部署过程中,在侦察来袭目标运动参数信息的基础上,可推测出敌机的航线方向和最大攻击距离d,设敌机飞行方向如图2所示,则可以根据保卫要地与敌相对位置信息,以局部要地为中心,d为半径,将多个要地划分为少量的防空区域,实现要地单点防空向区域防空的转变.为此,建立如下防空区域作图准则:

1)wj为首要考虑因素,wj从大到小排序,先以重要的要地开始作图,依次考虑次要要地.

图2 防空区域的划分Fig.2 Division of air defense zone

2)当次要要地已在重要要地防空区域内,则不再对其进行作图.

3)在wj相同情况下,相对敌目标位置更近的要地先作图.

在完成以上作图操作后,可以将多个单点要地划分为少量的防空区域,记为S={S1,S2,...,Sk},而根据优化算法将防空武器部署在各个防空区域的中心,既能最大火力地保卫防空区域中心的重点要地,也能兼顾保卫区域内部的其他要地,实现防空效能的最大化,同时从多要地转化为少防空区域的量化数据的减少更加有助于优化算法的收敛.

2.2 建立区域防空最优部署目标函数

采用不同防空区域的重要性系数为Wj,保卫性系数为Eij,其中Wj为j防空区域的重要程度,Eij为i武器对成功保卫j防空区域的概率.

假设第j个防空区域包括多个要地,S j=为该防空区域中心要地,dpq为sp要地与sq要地之间的距离,dpt为sp要地与st要地之间的距离,则第j个防空区域的重要性系数Wj和第i种武器系统对第j个防空区域成功保卫的概率Eij为:

防空部署可用矩阵X=(xij)m×k来描述,其中,xij为用于保卫j防空区域的i武器数量.

最优部署的目标函数是对防空区域的保卫效能指标达到最大,该保卫效能指标以成功保卫防空区域的数学期望为基础.

用一定数量的i武器成功保卫j防空区域的概率可表示为:

所有m类武器成功保卫j防空区域概率为:

数学期望为:

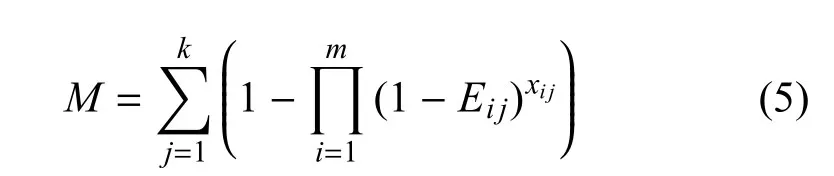
所以最优化的目标函数为:

约束条件如下:

2.3 遗传算法解算最优部署方案

根据遗传算法理论[17],结合区域防空部署问题的特征,设计了区域防空部署模型的遗传算法,为定量描述遗传算法求解过程,下面以具体实例来进行说明.

假设有A、B、C、D 4种型号的武器,共20个武器系统(A型数量n1为6个,B型数量n2为4个,C型数量n3为4个,D型数量n4为6个)用于保卫6个目标要地,保卫要地的坐标sj(=1,2,···,6)分别为s1(0,0),s2(−10,0),s3(0,15),s4(−40,40),s5(−50,40),s6(−50,0),其权重wj(=1,2,···,6)依次为(0.3,0.1,0.1,0.15,0.15,0.2);部署A型武器成功保卫要地sj的概率e1j(=1,2,···,6)为(0.30,0.40,0.60,0.30,0.50,0.40);部署B型武器成功保卫要地sj的概率e2j(=1,2,···,6)为(0.20,0.50,0.30,0.60,0.60,0.40);部署C型武器成功保卫要地sj的概率e3j(=1,2,···,6)为(0.80,0.50,0.20,0.30,0.70,0.40);部署D型武器成功保卫要地sj的概率e4j(=1,2,···,6)为(0.50,0.80,0.30,0.30,0.30,0.60),假设敌机来袭航线方向如图3所示,敌机攻击距离d为20 km,试求要地保卫效能最优时的区域防空部署方案.

首先根据要地分布情况、敌机攻击距离以及作图规则划分出S1={s1,s2,s3}、S2={s4,s5}、S3={s6}3个防空区域,如图3所示.

图3 防空区域的划分实例Fig.3 Example of the division of air defense zones

根据式(1)计算得出各防空区域Wj为

根据式(2)计算得出Eij为:

下面再利用遗传算法优化求解得出A、B、C、D 4种防空武器分别部署在S1、S2、S3的数量.

2.3.1 编码

对xij进行二进制编码,由于xij为非负整数,设xij最大取值为R=max{ni},Q(R)为R转化为二进制数时的位数,故每个部署方案所需串长为L=Q(R)×m×k,则第t个防空部署方案对应染色体为:

在上例中,xij最大为6,故R=3,因此L=3×4×3=36.

2.3.2 初始种群

初始种群选择的好坏影响算法的计算效率,所以,尽量将初始种群选在全局最优解附近,故既可减少迭代次数,又可更快得到满意解,根据区域防空作战部署的原则[18],提出根据要地重要性比例来产生初始种群的方法:

计算所有k个防空区域Wj的比例,根据式(1)计算结果,记为W1:W2:···:Wk.

计算相对重要程度.j防空区域的相对重要程度kWj为:

计算初始种群

根据上述方法得到的初始种群需满足作为约束条件的式(7).

对于A型武器部署在3个防空区域的数量x1j来讲,其变化范围为0～6,同时再考虑到A型武器成功保卫j防空区域的概率,分配其作战单元数分别为3,2,1,转化为初始种群为011010001,同理可得B型武器对防空区域部署的初始种群为010001001,C型武器对防空区域部署的初始种群为010001001,D型武器对防空区域部署的初始种群为011010001,最终得到第1 组初始种群01101 0001 010001001 010001001 011010001,同理,可生成第2～4 组初始种群,4 组初始种群分别为:

第1组初始种群 011010001 010001001 010001001 011010001.

第2组初始种群 100000010 011001000 100000000 100010000.

第3组初始种群 100010000 000000100 001000011 001000101.

第4组初始种群 001000101 000000100 100000000 100001001.

2.3.3 适应值

将区域防空部署优化模型中的目标函数值作为适应值,计算公式如下:

计算结果如表1所示.

表1 初始种群及其相关数据Table1 Initial population and related data

2.3.4 选择

按照部署方案的适应值F进行选择,每个个体的选择概率为通过随机方法来选择部署方案[19],被选中的部署方案(染色体)添入下一代染色体种群中,初始种群选择情况如表1所示.

2.3.5 交叉

交叉是产生新个体的重要方式,且是实现全局收敛的重要保障[20],为满足交叉操作可行性要求,采用单点交叉方法如下:

设Tp与Tq为配对交叉,其染色体分别为

交叉点选择在第s位,则交叉结果如下:

本例交叉点选择在第18位和第19位之间,确保交叉结果有效,根据选择结果,分别将1和2、1和3配对,交叉后新种群结果如表2所示.

表2 交叉运算结果Table2 Crossover operation result

2.3.6 变异

设定变异概率为P,对染色体随机一位进行变异操作,若变异后的染色体符合可行性要求,则填入下一代种群中.

按照以上步骤运行遗传算法程序,输出不同迭代次数下的最优解及其适应值.

2.4 遗传算法模型优化分析

实际遗传算法模型设计时,有很多因素影响了迭代结果的收敛速度和收敛质量,故本文从不同的影响因素角度来分析针对区域防空遗传算法的最优化因素组合.

从不同变异概率的角度来分析,分别取变异概率为P变异= 0.01、0.05、0.1、0.2、0.3,交叉概率为P交叉=0.6,迭代次数为ger=1 000,初始种群适应值为F初始=0.7,仿真结果如图4所示,可以看出,随着变异概率逐渐增加,结果越快收敛且收敛值越高,但当变异概率为0.2后,若继续增加变异概率,因变异趋势无法控制,收敛效果出现下降,因此,本文采用变异概率P变异=0.2 作为区域防空遗传算法的最优化变异概率因素.

图4 不同变异概率下适应值Fig.4 Fitness value under different mutation probability

从不同交叉概率角度来分析,分别取交叉概率为P交叉=0.2、0.4、0.6、0.8,变异概率为P变异=0.2,迭代次数为ger=1 000,初始种群适应值为F初始=0.7,仿真结果如图5所示,可以看出,随着交叉概率逐渐增加,结果越快收敛且收敛值越高,但当交叉概率为0.6后,若继续增加交叉概率,因交叉趋势无法控制,收敛效果出现下降,因此,本文采用交叉概率P交叉=0.6 作为区域防空遗传算法的最优化交叉概率因素.

图5 不同交叉概率下适应值Fig.5 Fitness value under different crossover probability

从不同迭代次数的角度来分析,分别取迭代次数为ger=10、100、300、600、1 000、10 000,变异概率为P变异=0.2,交叉概率为P交叉=0.6,初始种群适应值为F初始=0.7,仿真结果如图6所示,可以看出,随着迭代次数的逐渐增加,结果越快收敛且收敛值越高,但当迭代次数为1 000后,若继续增加迭代次数,因遗传算法模型已到达收敛峰值,收敛效果明显变化,因此,本文采用迭代次数ger=1 000 作为区域防空遗传算法的最优化迭代次数因素.

从不同初始种群适应值的角度来分析,分别取初始种群适应值F初始=0.3、0.4、0.5、0.7,变异概率为P变异= 0.2,交叉概率为P交叉= 0.6,迭代次数为ger=1 000,仿真结果如图7所示,可以看出,随着初始种群适应值逐渐增加,结果收敛越快,当初始种群适应值为0.7 时,只需要迭代计算86次即可完成遗传算法模型的收敛,因此,本文采用初始种群适应值F初始=0.7 作为区域防空遗传算法的最优化变异概率因素.

图6 不同迭代次数下适应值Fig.6 Fitness value under different iteration times

图7 不同初始种群适应值下收敛效果Fig.7 Convergence effect under different initial population fitnes

综上分析所述,区域防空遗传算法的最优化因素组合为变异概率P变异= 0.2,交叉概率为P交叉= 0.6,迭代次数为ger=1 000,初始种群适应值为F初始= 0.7,对于本例,经过1 000次迭代优化,可得最终结果为:X=(x11,x12,x13,x21,x22,x23,x31,x32,x33,x41,x42,x43)=(0,0,6,0,4,0,3,0,1,1,0,5),最大适应值为maxF=0.799 9,即第1个防空区域S1部署C型武器3个单元和D型武器1个单元,第2个防空区域S2部署B型武器4个单元,第3个防空区域S3部署A型武器6个单元、C型武器1个单元和D型导弹5个单元.

值得注意的是,对于本实例,如果前期没有将多个要地转化为少量的防空区域来减少计算量,将大大增加遗传算法的可编程性和最优解求解效率,且如果在初始种群中的选择不合适的话,可能无法迭代得到全局最优解,由于约束条件的存在使得染色体个体在选择交叉点、交叉方法和变异方式上都受到制约,为了避免这个问题,一方面可以在设计产生初始种群时,可以根据先验知识而不是通过随机方式来产生,另一方面可以适当增大初始种群中染色体个体的数量,将各染色体个体之间的差异明显化,从而能更有效地达到全局最优解.

3 结论

本文提出了一种将单点要地防空部署转化为区域防空部署的方法,建立了区域防空部署方案的数学模型,并将遗传算法应用于区域防空部署的优化求解,为该问题的解决提供了一个简单有效的途径.实例证明,该方法能够取得良好的部署效能,在一定的时间内即可搜索到全局或近似全局的最优解,从而为我国区域防空部署的制定提供科学的、有效的支持.

在此,要特别感谢我的老师邱令存研究员,邱老师不辞辛劳,多次与我就论文中的核心问题展开细致入微地探讨,并给我提出切实可行的建设性意见.“授人以鱼,不如授之以渔”,请允许我向尊敬的邱令存老师表示真挚的谢意.