基于微分对策的拦截机动目标协同制导方法

于江龙 董希旺,2 李清东 吕金虎,2 任章,2

未来战争将会呈现高动态、强博弈的特点,智能化体系作战博弈对抗将会成为未来作战的趋势,单弹拦截智能化恶意机动目标难度将会大大提升,多弹协同拦截是应对恶意机动目标的重要作战方式,多弹进行设备与功能的差异配置,凭借数量和策略优势,采取合适的协同博弈拦截策略,能够实现对恶意机动目标的有效拦截[1−5].

然而经典的多导弹协同制导策略大多关注攻击时间的同时性[6]、攻击角度的一致性[7],或者二者兼备[8],适合拦截静止的或者低速小机动的目标.因此需要研究适合拦截机动目标的新型协同导引律.

在博弈对抗场景下,基于微分博弈理论的导引律并不需要目标的机动信息,能够充分发挥拦截导弹的机动性能与机动策略.文献[9−10]针对单枚导弹拦截单目标的微分对策制导问题开展了研究,文献[11−15]运用动态博弈理论设计了最优协同策略导引律.近年来,学者对三体(拦截导弹、目标和防御导弹)协同制导问题进行了广泛的研究[16−18],其原理就是协同微分对策制导的应用.

本文将重点研究基于微分对策的协同制导问题,构建新型的协同微分对策导引律,实现多导弹对恶意机动目标的有效拦截,以期为未来信息时代的防空反导体系建设及智能作战指挥与控制系统的发展提供可能的技术支撑.

1 基础知识

1.1 动态系统的微分对策问题

考虑以下一般的非线性动态博弈系统[9];

其中,x∈Rn为上述系统的状态变量,(u,v)为博弈双方的控制量,t表示时间,t0＞0和tf＞0为博弈的初始时刻和终止时刻.

博弈问题的终端任务状态集为:

选取代价函数为

其中,h(t,x(t),u(t),v(t))为任意的给定实值函数,且有

µ的维数与φ(t,x(t))是匹配的,g(t,x(t))是附加终端状态集合.

引理1[19],设U和V是两个闭区域且边界光滑,函数f(t,x,u,v)和h(t,x(t),u(t),v(t))连续可微且在[t0,tf]×Rn×U×V的有界子集中关于(t,x)是一致李雅普诺夫连续;函数g(t,x(t))和φ(t,x(t))在[t0,tf]×Rn的有界子集中一致李雅普洛夫连续且连续可微.如果(u∗(t),v∗(t))是微分对策问题的鞍点,则(u∗(t),v∗(t),x∗(t))满足以下方程:

其中,x∗(t)是相对于鞍点(u∗(t),v∗(t))的最优轨迹,˜t是从初始状态沿着最优轨迹到达目标集边界所用的时间.

1.2 代数图论基础

在多导弹的协同制导问题中,每枚导弹除了对目标进行制导,还受到其他邻居导弹的影响,而形成协同制导,本文利用代数图来描述描述导弹之间的相互影响.

定义集合V={1,2,···,M} 用来表示多导弹集,ε ⊆V×V用来表示导弹之间对应的边集,用图G=G(V,ε)来描述多导弹之间的拓扑关系,边集中的边(i,j)用来表示信息从导弹i流向j,如果满足(i,j)∈ε ⇔(j,i)∈ε,则(i,j)为双向边,如果图G中每一个边都是双向边,则称该图为无向图;反之,如果图G中存在一个边是单向的,则称之为有向图.

如果(j,i)∈ε,则j是i的一个邻居导弹,定义一个图的邻接矩阵A=[µij] ∈RM×M,如果(j,i)∈ε,则µij＞0,反之,则有µij=0,定义图G的入度矩阵D=[dij]∈RM×M,如果i≠j,则dij=0,如果i=j,则有dij=

对于无向图G,如果任意两枚导弹之间都存在一条路径,则称该图是连通的;对于有向图G,若对于任意两枚导弹之间都存在一条路径,则该图是强连通的,在图G中,存在一枚导弹,到其他任意一枚导弹都存在路径,则图G含有一棵有向生成树.

2 协同制导问题描述

2.1 协同微分对策制导问题建模

多导弹凭借数量和策略优势,能够降低目标逃逸区域、增大有效杀伤区,进而实现对恶意机动目标的有效拦截,本文考虑N(N≥2)枚导弹对1枚目标的协同制导问题,如图1所示.

图1 多导弹协同制导示意Fig.1 Schematic of multiple missile cooperative guidance

在本文中,将三维协同制导问题分解为纵向制导与横向制导的两个二维制导问题.

在二维平面内的惯性坐标系下,导弹i和目标T运动学模型可以表示为:

其中,i∈{1,2,···,N},导弹i和目标T的坐标分别为(xi(t),yi(t))和(xT(t),yT(t)),VM,i(t)为飞行器i速度大小,VT(t)为目标速度大小,γM,i(t)、γT(t)分别为速度角(速度倾角或者速度偏角,本文简称速度角).

根据上述模型,本文研究的是运动学层面的制导问题,也就是通过速度角的控制实现位置回路的制导,此外,本文研究多枚同样配置(同构)导弹的协同制导问题,暂不考虑多导弹之间的性能匹配问题.

在二维平面内视线坐标系下,可以将式(1)转化得到弹目相对运动学模型:

其中,λi(t)表示二维平面内的视线角,θM,i(t)、θT,i(t)分别表示导弹i和目标的前置角,在本文中,假设导弹和目标的速度均为常值.

2.2 协同微分对策问题描述

在经典的微分对策制导问题中,微分对策制导问题一般描述为单枚导弹经过最优机动实现对目标的拦截,而在现有的协同微分对策制导问题中,大多考虑三体协同微分对策制导问题[16−18];或者仅考虑了多弹在过载约束下的拦截问题,而没有考虑多弹之间的信息交互问题[11−15].

本文考虑了多导弹之间的信息交互问题,多导弹之间的通信拓扑满足下列假设.

假设1[20],多导弹之间的通信拓扑图用G描述,G为一个连通的有向图,且每枚导弹均能够获得对于目标的制导信息.

多导弹协同微分对策制导问题的核心一般包括两个方面,一是协同制导的模型,二是代价函数的选择.上节已给出运动学层面的制导问题.本节核心在于给出协同微分对策制导问题的代价函数,包括以下方面.

考虑初始制导时刻为0,首先定义各枚导弹对目标的拦截时刻分别为tF,i,i∈{1,2,···,N}.

1)协同的代价建模

多枚拦截导弹在各自的拦截时刻,如果他们之间的相对距离越小,则说明多枚导弹实现了准同时拦截,在一定程度上表征了多拦截导弹之间的拦截时间一致性,因此,定义一个代价函数为:

2)拦截的代价建模

本文考虑的协同制导问题在于实现多枚导弹对目标的拦截,如果拦截时刻导弹i和目标T之间的相对距离(可近似为脱靶量)越小,则代表了导弹i对目标T的拦截效果越好.因此,定义一个代价函数为:

其中,µi表示导弹i和目标T的通信权重.

3)能量的代价建模

拦截过程中,期望导弹机动的范围越小越好,这样能够节省拦截过程中的能量,因此定义一个代价函数为:

其中,βi＞0,γM,i,0为常数,表示初始时刻的最佳速度角(其值可参考文献[9]),对于拦截导弹来说,越小,则代表拦截轨迹约平缓.为了将微分对策中的目标最优逃逸问题引入,在这里将修正为J3,即:

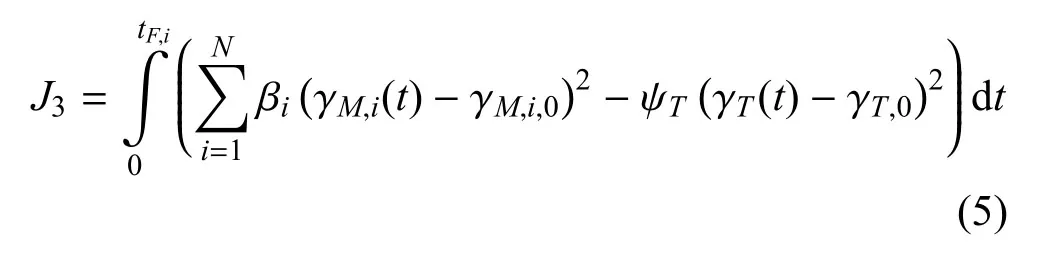
其中,ψT＞0,γT,0也为一个常数,表示目标T初始时刻的最佳速度角(其值可参考文献[9]).

因此,多导弹和目标组成了一个最优拦截追逃的协同微分对策制导问题,控制输入为(γM,i(t),γT(t)),代价函数定义为:

可以看出,代价函数(6)是由子代价函数(1)、(3)、(5)组成的,因此代价函数(6)表征了多弹协同制导过程中需要同时满足协同约束、拦截约束和能量约束,此外,3个子代价函数的加权系数可以通过参数µik、µi、βi、ψT来进行调节.

3 协同微分对策导引律设计

在本节中,将给出协同微分对策导引律的设计过程.

针对拦截导弹来说,期望J最小化;针对目标来说,期望J最小化,因此定义哈密顿函数为:

其中,λi1(t)、λi2(t),i∈{1,2,···,N},λT1、λT2为伴随状态,.

对于拦截导弹i来说,由

可得拦截导弹i的协同微分对策导引律:

根据引理1,伴随状态动态特性及其终端值为:

因此,有:

可以看出,协同微分对策导引律(9)是一个超越方程,如果βj≡0,则式(9)有解析解;而如果βj是一个小量的话,可以用牛顿迭代法进行精确的数值求解,如果βj取小量,则式(9)的近似可行解为:

此外,对哈密顿函数H求二次微分,有

因此,微分对策导引律(9)在一定范围内是最优制导问题的解.

用同样方法,可得到目标最优逃逸导引律:

其中

tF,T为目标逃逸成功的时刻.

值得注意的是,导引律(9)和式(15)中并不显含时间t,而是含有拦截时刻tF,i,一般来说,tF,i的获取相对复杂,可采用初始相对距离除以相对速度得到,也可通过分段求解进行计算tF,i.

此外,如果目标T有多个,则本文的问题转化为多对多协同博弈对抗的问题.从目标角度来看,协同拦截导引律构成了协同突防导引律.因此,本文方法对多对多协同博弈对抗问题求解具有一定的启发.

4 仿真试验分析

本节将给出两个仿真示例来说明本文提出的协同微分对策导引律的有效性.

两枚导弹和目标的初始阵位设置为:xT(0)=以及VT=400 m/s,γM,1=35◦,γM,2=32◦,γT=180◦.

两枚导弹之间可以互相通信,两枚导弹也均能获得目标的信息,因此多导弹与目标之间的通信拓扑结构满足假设1的条件.

协同微分对策导引律的目标是使得代价函数J取极小值,而拦截效果则与导弹、目标的速度以及其他设计参数有关,实际拦截情况应以仿真脱靶量为准.本节主要关注多弹对目标的拦截情况,目标过载设置为aT=0.5 g,仿真结果如图2和图3所示.

多导弹协同微分博弈模式下的拦截轨迹曲线如图2所示,多导弹在拦截过程中的过载曲线aM,1(t)和aM,2(t)如图3所示,可以看出过载是有界的,此外,两枚导弹的最终拦截脱靶量为0.55 m和0.62 m,而且两枚导弹的拦截时间之差为0.17 s,这意味着两枚导弹在导引律(9)对目标实现了对目标的协同拦截.

为了证明本节算法有效性,增加一组仿真实验,初始状态与本节相同,导弹导引律为比例导引法,导引系数为4,仿真结果如图4和图5.

图2 多导弹协同拦截目标的轨迹Fig.2 Trajectories of multiple missile cooperative interception against target

图3 多导弹协同拦截目标的过载曲线Fig.3 Overload curves of multiple missiles cooperative interception against target

图4 多导弹比例导引律下拦截目标的轨迹Fig.4 Trajectories of multiple missiles cooperative interception against target using proportional guidance law

图5 多导弹比例导引律下拦截目标的过载曲线Fig.5 Overload curves of multiple missiles using proportional guidance laws

5 结论

本文研究了智能化体系作战博弈对抗场景下的协同博弈制导问题,基于微分对策理论设计了一种新型的多导弹协同导引律,进行了协同微分对策导引律与比例导引律的对比仿真实验,证明协同导引律较经典的比例导引律具有更好的拦截效果.此外,协同微分对策导引律可以进一步转化为多目标协同突防导引律,及多对多协同博弈导引律,因此,本文方法对于多对多协同博弈对抗的问题求解具有一定的启发性,后续研究中,将进一步考虑多弹之间的过载匹配、功能匹配问题.