重力梯度仪仿真系统设计

刘 杰, 闫 妍, 申梦娴, 刘乾坤, 罗伟东

(1.吉林大学 仪器科学与电气工程学院, 长春130061; 2.中国地质调查局 广州海洋地质调查局, 广州510000)

0 引 言

重力梯度仪是用于测量重力梯度张量的仪器, 是目前探测地球的先进手段之一, 在能源勘探、 航空、地形恢复等方面发挥着重要的作用[1]。 重力梯度在空间上有9 个分量, 其中5 个分量是独立的, 利用这5 个分量的数据及其变化即可以对地球上物质发生的变化进行预测。 目前国内外常见的重力梯度仪主要有4 种[2]: 旋转加速度计重力梯度仪、 静电加速度计重力梯度仪、 超导重力梯度仪和冷原子重力梯度仪。笔者所研究的全张量旋转加速度计重力梯度仪在常温下工作, 非常适合应用于地下资源勘探、 海洋技术以及惯性导航等领域[3-6]。 为了模拟旋转加速度计重力梯度仪的工作原理, 研究重力梯度仪信号处理的方法, 笔者分别对全张量重力梯度仪和单圆盘重力梯度仪进行了仿真。

1 设计方案

旋转加速度计重力梯度仪的4 个加速度计对称、 正交地安装在一个低速转台上( GGI: Gravity Gradient Instrument), 加速度计的敏感轴沿转台的切线方向, 而且相对的两个加速度计敏感轴方向相反,如图1 所示[7]。 工作时, GGI 转台以特定的角速率旋转, 单个GGI 转台能测量部分张量的重力梯度, 将3 个相同的GGI 转台在空间正交安装, 构成全张量重力梯度仪, 能实现全张量的重力梯度测量, 如图2所示[6]。

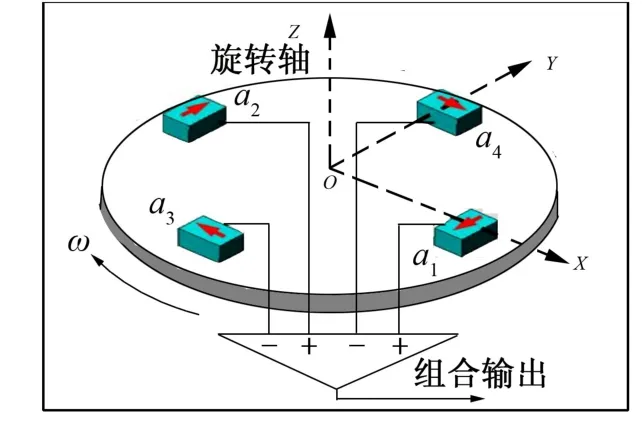
图1 旋转加速度计重力梯度仪GGI 示意图 Fig.1 Rotary accelerometer gravity gradiometer GGI schematic

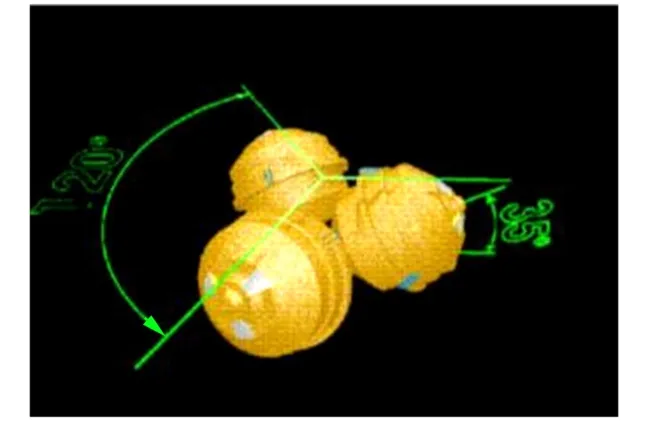
图2 全张量重力梯度仪结构示意图Fig.2 Schematic diagram of full tensor gravity gradiometer

旋转加速度计重力梯度仪的系统仿真流程图如图3 所示。 以单圆盘为例, 计算机A 模拟正交放置的4 个加速度计输出数据, 通过D/ A 转换为模拟信号, 并对4 路加速度计信号进行求和求差运算, 再通过A/ D 将调理过的信号经过串口发送到计算机B 中, 由计算机B 对数据进行滤波和解调。

图3 重力梯度仪仿真系统框图Fig.3 Gravity gradiometer simulation system block diagram

2 信号产生

2.1 重力梯度测量原理

空间质量受到的重力是由地球引力和地球自转引起的惯性离心力构成, 重力位函数是一个标量函数, 它对各个方向的偏导数等于重力在对应坐标轴上的分量。 重力位函数为

其中ωe是地球自转角速度,r是空间质量到地心的距离,x,y分别是空间质量在固地坐标系相应坐标轴上的分量,M是地球的质量,G是万有引力常数。

重力加速度是重力位沿着重力方向的一阶偏导数, 重力梯度是重力位沿重力方向的二阶偏导数。 各个方向的重力加速度为

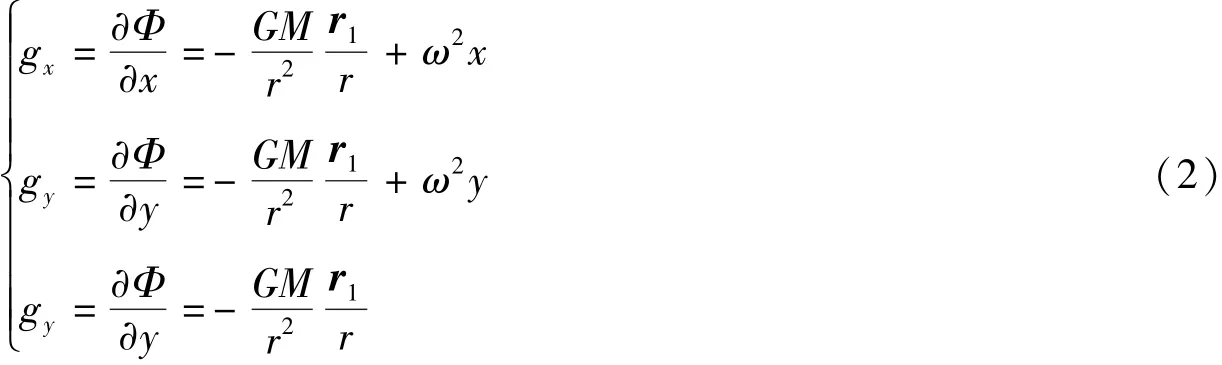
对重力位在各个方向上求二阶导数可得到重力梯度

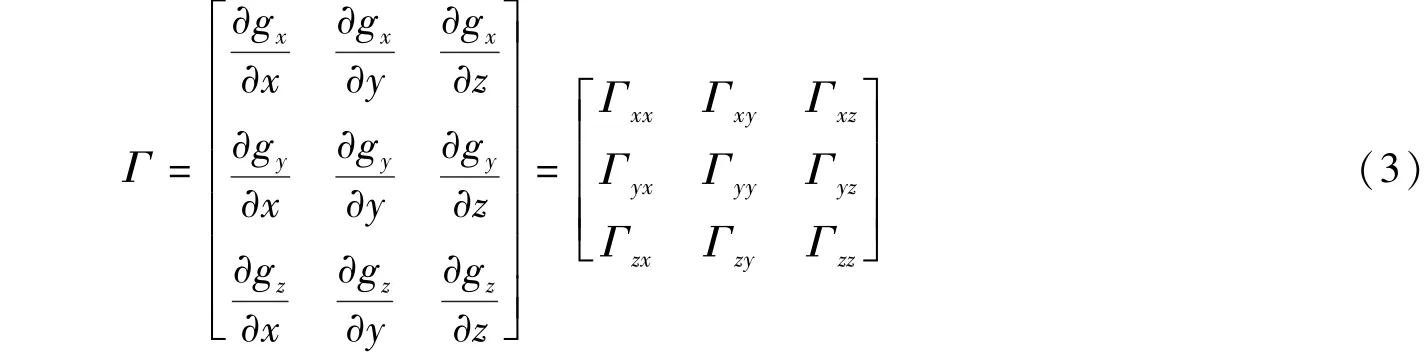
其中Γxy=Γyx,Γxz=Γzx,Γyz=Γzy,Γxx+Γyy+Γzz=0。

2.2 加速度计测量原理

如果忽略地球自转角速度重力梯度仪平台相对于地球坐标系的转动角速度和圆盘自转角速度, 根据摆式加速度计输出的数学模型[5-8]可导出单个加速度计的输出结果为

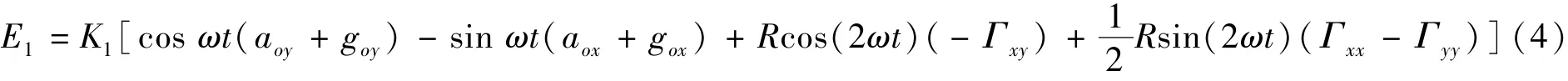
水平圆盘的输出为E=(E1+E2)-(E3+E4), 在理想条件下, 当4 个加速度计的标度因数一致时, 圆盘输出为E=4KRcos(2ωt)(-Γxy)+2KRsin(2ωt)(Γxx-Γyy)。

下面推导全张量重力梯度仪的加速度计输出模型[3,7-9]。 全张量重力梯度仪由3 个GGI 组成, 安装在由陀螺仪稳定的平台上, 3 个GGI 的轴线互相垂直。 为了简化计算, 以3 个圆盘的正交旋转轴建立平台坐标系OXYZ, 再以旋转轴为法线在每个圆盘上建立测量坐标系OiXiYiZi(i=1,2,3), 如图4 所示。 根据3 个圆盘之间的位置关系, 已知1 个质量块在1 个圆盘坐标系位置的情况下可推导出相同的质量块与另1 个圆盘的位置关系。 把质量块看作一个质点P, 已知质点P在平台坐标系下的坐标为(x,y,z), 平台坐标系的重力加速度为g=(gx,gy,gz), 则将平台坐标系转换到每个GGI 的测量坐标系, 圆盘1 中心的重力加速度为g1=(g1x,g1y,g1z), 圆盘2 中心的重力加速度为g2=(g2x,g2y,g2z), 圆盘3 中心的重力加速度为g3=(g3x,g3y,g3z)。 因此可得到每个GGI 上的加速度计输出。

3 信号调理

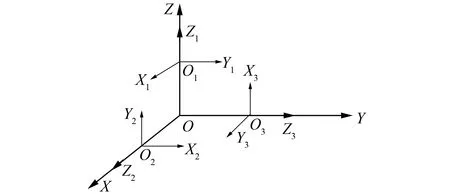
图4 坐标系示意图Fig.4 Coordinate gravity gradiometer simulation system block diagram

信号调理的目的是将4 个加速度计的测量信号相加减, 消除了动基座引起的共模角加速度和线速度对重力梯度仪输出的影响并放大了梯度信号[4]。 该部分功能通过硬件电路实现, 对重力梯度仪进行半实物仿真。 半实物仿真将某些非线性度较高的关键部件实物引入仿真回路, 避免全数字仿真中由于建立非线性部件数学模型的误差, 从而可以提高仿真的可信度。

为使单个圆盘的4 个加速度计信号同时输出, 选用DAC7617 4 路串行输入、 12 位电压输出的数模转换器将计算机产生的加速度计数据转换为加速度计信号, 电路如图5 所示。 为了提高信噪比, 选用了LT1814 4 运放芯片搭建求和求差放大电路, 电路图如图6 所示。 4 路信号经过求和求差放大电路后,利用单片机STM32F103ZET6 内部集成的AD 通道对调理后的3 路信号(E1+E2),(E3+E4),(E1+E1)-(E3+E4)进行采集[10], 并通过串口发送到计算机中进行后续的数据解调处理。 串口电路如图7 所示。

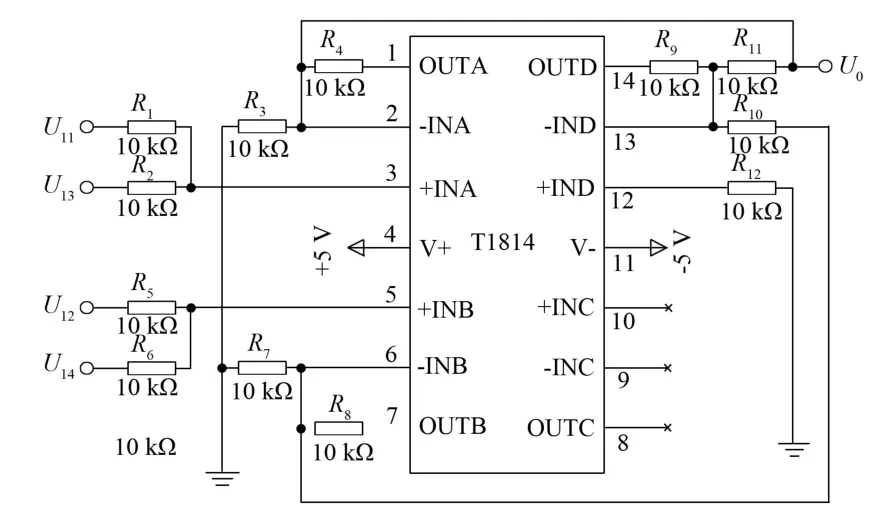
图6 信号调理电路Fig.6 Signal conditioning circuit

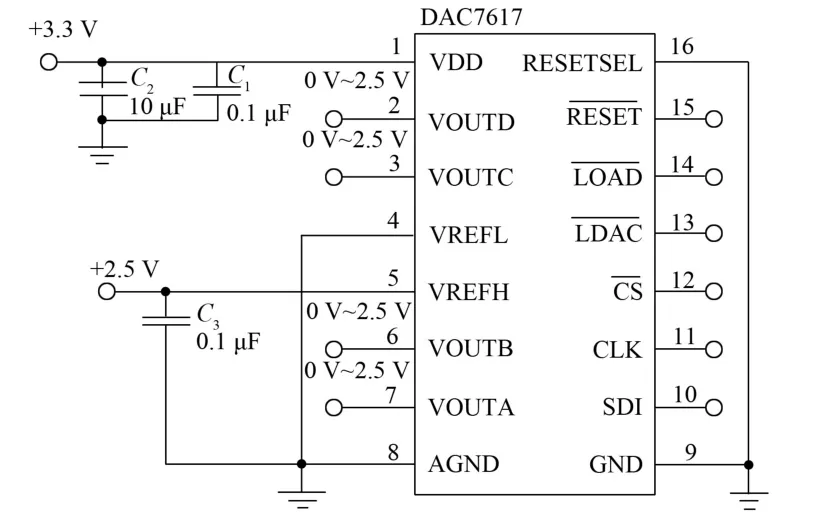
图5 DAC7617 驱动电路Fig.5 The driver circuit of DAC7617

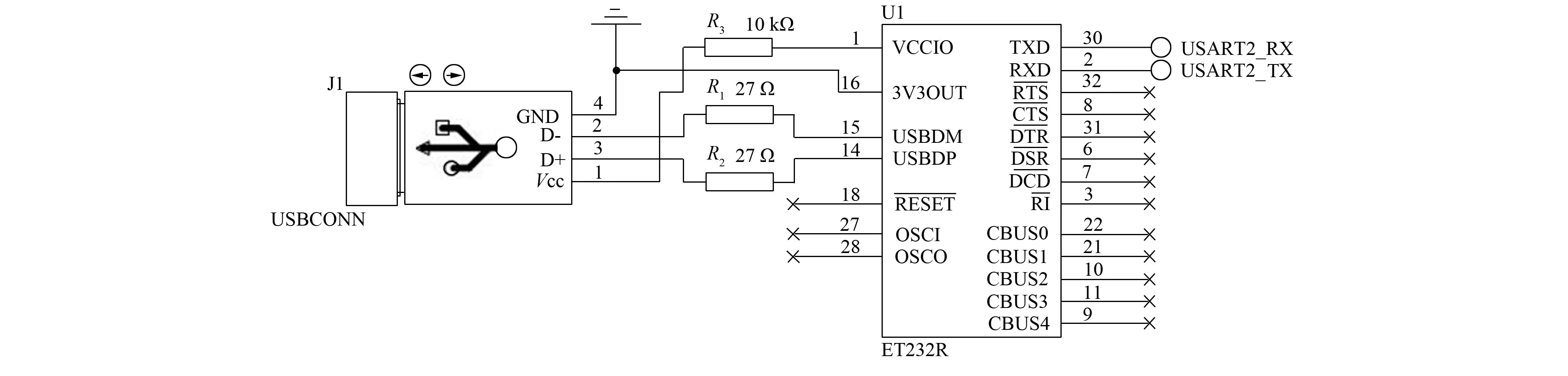
图7 串口驱动电路Fig.7 Serial port driver circuit

4 信号解调

信号解调[11-16]与反馈模块由计算机B 完成, 该部分主要包括滤波、 数据解调以及加速度计标度因数不一致信息反馈。 整体流程图如图8 所示, 主要过程为: 下位机通过串口向计算机B 传输数据, 并将数据存储在读取缓冲区中, 不断进行读取, 将数据存储在数组中; 为了提高信号的信噪比和解调精度, 在解调前通过中值滤波器对数据进行滤波; 信号解调在滤波后进行, 该部分能将加速度计标度因数不一致量及重力梯度值进行解调, 并利用PID(Proportion Integral Derivative)控制器将标度因数不一致信息反馈给计算机A, 计算机A 对标度因数调整后重新发送数据, 计算机B 进行处理, 直到解调出的重力梯度满足精度为止。

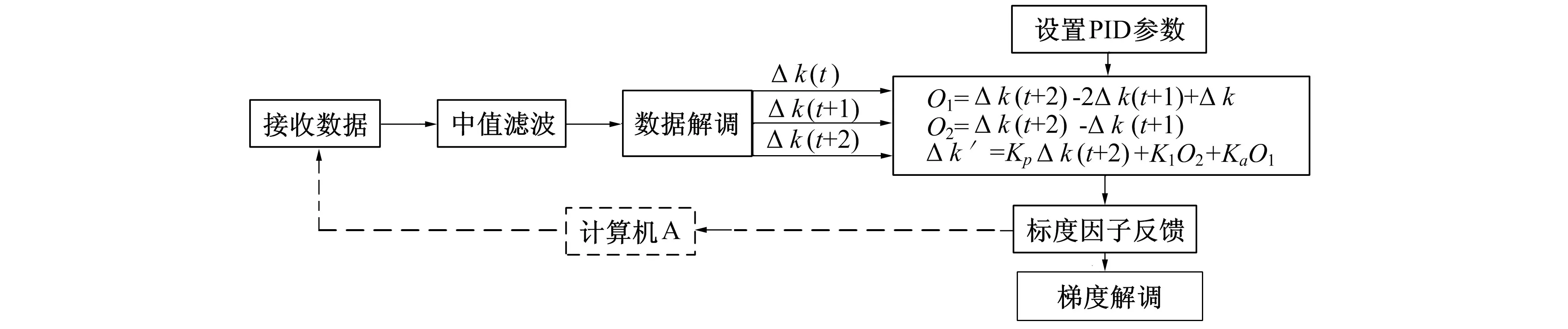
图8 信号解调框图Fig.8 Signal demodulation block diagram

由信号产生部分可知, 当加速度计标度因数不一致时, 以水平圆盘为例, 单个圆盘的输出为

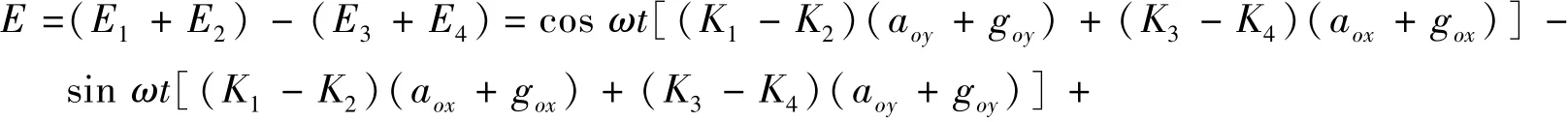
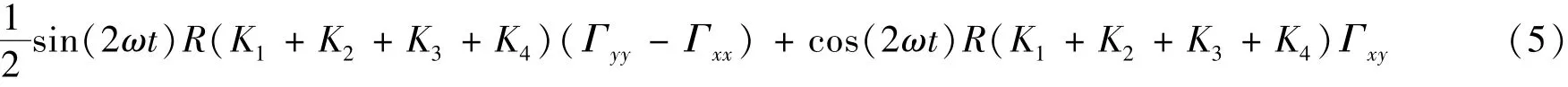
从式(5)可以看出, 在输出信号的一倍频处解调[3-7], 可得到加速度计1 和加速度计2 的标度因数不一致量及加速度计3 和加速度计4 的标度因数不一致量, 通过串口, 将标度因数不一致量反馈给计算机A,经过调整使两两加速度计的标度因数达到一致。 通过对平台输出信号进行积分解调, 即输出信号与相乘后积分, 可得重力梯度值。

通过对两个相对的加速度计的标度因数实时反馈调节, 可以有效的抑制平台的平动加速度对输出信号的影响。 笔者利用增量式PID 控制器, 该控制器在进行控制时需要3 个时刻的输出结果。 通过设置PID 的3 个参数(Kp,Ki,Kd)调整加速度计标度因数, 这3 个参数决定了控制过程的过渡时间和稳定性。经过计算得到合适的PID 参数后, 将经过PID 调节后的结果反馈给计算机A。

5 仿真结果

假设地下异常体为理想的球体, 以3 个圆盘的正交旋转轴建立平台坐标系OXYZ, 参数设置如表1所示。 重力梯度仪的参数设置也如表1 所示。 根据加速度计的工作原理, 运用LabVIEW 仿真全张量旋转加速度计重力梯度仪产生12 个加速度计数据, 并对数据进行解调, 得到全张量的重力梯度值。 正演仿真结果和解调结果如表2 所示。 在实验中, 多次对表1 中的参数设置进行更改, 可以在表2 看到对解调数据精度的影响。 经过多次测试, 发现圆盘半径为1 m, 采样频率为16 Hz 时, 数据解调的精度最高, 验证了笔者所使用的数据解调方法是有效可行的。

表1 实验参数设置Tab.1 Experimental parameter setting

表2 测试结果Tab.2 Test results

下面以单圆盘为例, 引入部分硬件电路, 对重力梯度仪进行半实物仿真, 通过对Γxx-Γyy和Γxy进行解调, 进一步验证该数据解调方法的可行性和可靠性。 圆盘的参数设置如表1 所示, 调整加速度计的标度因数, 通过硬件对信号进行运算, 再由计算机B 对信号进行解调处理, 由于硬件电路引入部分随机噪声, 因此相当于4 个加速度计的标度因数存在不一致量。 实际上, 在每个GGI 上的加速度计的摆放都不可能保证完全的正交, 通过调整加速度计的标度因数可以消除这种误差。 在仿真过程中由计算机B 将标度因数调整量和解调结果反馈给计算机A, 对输出数据进行调整, 使解调出的梯度值精度满足要求。 受到硬件电路的限制, 所选用的ADC 和DAC 都是12 bit 且3.3 V 供电, 因此测量的重力梯度值的范围在-5 000 E ～+5 000 E, 精度可达到100 E。

单圆盘的仿真结果如表3 所示。 首先, 设置采样点数为64, 每隔125 ms 从计算机A 发送一组加速度计数据到下位机。 发送格式为“0num64N16fsaAbBcCd”, 其中, 0 为发送数据的序号, 作为接收数据的校验, 64 为采样点数, 16 为采样频率, “a”,“b”,“c”, “d” 分别表示4 个加速度计的输出数据。 接收格式为 “ek1Eek2At1Bt2”, 其中 “ek1” 为加速度计1 的标度因数调整量, “ek2” 为加速度计3 的标度因数调整量, “t1” 为 Γxx-Γyy的解调结果, “t2” 为 Γxy的解调结果。 计算机A 将数据发送到硬件电路进行处理后发送给计算机B, 计算机B 的接收格式为 “0num64N16fss1As2Bs3”, 其中 “s1” 和 “s2” 分别为圆盘上相对两加速度计相加后的数据, “s3” 为 “s1-s2” 后的数据。 计算机B 解调后将调整量和解调值反馈给计算机A, 发送格式与计算机A 的接受格式相同。

通过对表3 中的数据进行分析可知, 在单圆盘重力梯度仪半实物仿真的精度在100 E 内。 其误差主要来源于以下几个方面: 1) 数模转换的精度低, 在转换过程中丢失部分数据; 2)单片机内部集成的ADC精度低且在0 ～0.5 V 之间存在非线性区; 3) 信号经过硬件电路后含有噪声和工频干扰。 因此, 在后续的研究工作中, 为了提高重力梯度仪的精度, 一方面可以选用精度更高的D/ A 和A/ D, 尽可能多地保留数据的精度位数, 另一方面改进硬件电路, 比如采用差分输入差分输出的电路形式抑制共模干扰, 电源处做好电磁屏蔽等减少信号通过硬件电路产生的噪声。

表3 单圆盘半实物仿真测试结果Tab.3 Test results of hardware in the loop simulation of single disk

6 结 语

笔者依据旋转加速度计重力梯度仪的测量原理, 对地下某异常体引起的重力梯度异常值进行了计算, 简化梯度模型后, 得到了全张量的重力梯度。 通过模拟加速度计数据, 对全张量重力梯度仪进行了仿真、 运算和数字解调。 以单圆盘为例, 对重力梯度仪进行了半实物仿真, 研究了旋转加速度计重力梯度仪的信号产生原理, 加速度计信号解调重力梯度值的方法以及反馈标度因数不一致的调整方法, 为重力梯度仪硬件设计提供理论和技术支持。