基于ELM的混联式输送机构自适应反步控制

袁 伟, 王 曜, 卢佳佳

(1.江苏科技大学 电子信息学院,镇江 212100)(2.江苏大学 电气信息工程学院,镇江 212013)(3.阜阳职业技术学院 工程科技学院,阜阳 236031)

现有的汽车电泳涂装自动化输送系统多为串联机构,存在着承载能力较差,多车型混线生产柔性化水平不高等问题[1],混联输送机构将串联与并联机构进行有效结合,既保留了串联机构工作空间大、运动方式灵活的优点,又能弥补其结构稳定性差,承载力小和运动精度低的不足．

混联输送机构具有多变量、强非线性和高度耦合性的特点,相对于传统的运动学控制方法,采用动力学控制能取得更好的控制效果．常用的动力学控制方法通常依赖于精确的动力学模型,然而由于摩擦力、模型参数摄动等因素,一般很难得到精确的动力学模型;其次,电泳槽液无规则流动、电机运行过程中的抖动以及其他未知复杂干扰,也将影响混联机构的控制性能,因此需在控制方法中采用有效的干扰抑制策略进行消除．目前对混联机构采用的控制策略主要有PID控制,计算力矩控制、变结构滑模控制,自适应控制等[2]．PID和计算力矩控制等无模型动力学控制方法,虽容易实现,却只能补偿特定的扰动和参数变化;滑模控制对模型参数及外界扰动不敏感,但产生的抖振现象导致其难于运用于实践;自适应控制可以实现基于模型的高精度控制,但复杂的建模和大量的计算给使用带来不便．

反步法根据被控对象的结构特点,分步反向递进设计整个系统的Lyapunov方程,所构建的控制器结构清晰、系统规整,在实现不确定非线性系统的自适应控制方面有明显的优越性,广泛应用于各类非线性控制系统．反步法结合先进控制技术、智能控制技术应用于机器人控制,已成为国内外相关研究人员的研究热点．文献[3-5]针对变刚度机械臂高度非线性特点,设计了结合滤波器的反步控制器．文献[6]采用反步控制技术设计机械臂位置/力控制器,结合自适应算法修正动力学参数,使时滞柔性机械臂实现位置/力信号跟踪控制．文献[7-9]通过反步设计与滑模控制方法相结合,设计反步滑模控制器应用于机械臂的控制,取得了较好的抗扰性,但是滑模控制会产生抖振问题．

扰动观测器估计未知扰动和模型不确定性,然后对系统进行补偿,从而改善系统的抗干扰能力,因此基于扰动观测器的控制策略已在机器人中广泛应用．文献[10]设计一种带扰动观测器的自适应反步滑模控制方法,在线估计扰动并调整控制输出,实现了柔性踝关节康复机器人动态条件下的精准跟踪．文献[11-12]基于观测状态和逼近模型的反演控制器，利用神经网络观测器对机械臂动力学模型进行辨识设计.文献[13]针对不确定严反馈系统,结合反步法与神经网络技术,使用Barbalat引理进行稳定性分析,确保控制器达到误差要求,并在多关节机械臂模型上进行验证．文献[14]采用径向基函数(radial basis function，RBF)神经网络与滑模控制相结合的方法,在保证系统控制的鲁棒性的前提下,有效地减小了并联机构控制系统中滑模抖动问题．文献[15] 通过引入动态面技术解决了反步设计中存在的“微分爆炸”问题,并结合RBF神经网络逼近未知函数,实现了机器人跟踪误差任意小．带扰动观测器一般只能估计特定条件的扰动，(back propagation，BP)神经网络和RBF网络可以实现对未知部分的良好逼近,但是BP网络学习速度慢、容易陷入局部极小值;RBF网络隐含层神经元基函数中心矢量值及基宽度的选择也依赖经验和反复调试,选择不当反而会影响控制效果．

结合以上分析,文中以混联式输送机构为研究对象,采用反步法设计动力学控制器,并将模型不精确部分及未知外部干扰共同作为集总扰动项,采用神经网络极限学习机(extreme learning machine，ELM)进行逼近,提出一种基于ELM的自适应反步控制器,最后通过仿真验证其有效性．

1 系统建模

混联式输送机构由行走机构和翻转升降机构组成,车体固定在机构连接杆中部,实现车体在电泳槽液中的前进、翻转、升降功能，其结构如图1．因行走机构结构简单且做匀速前进,无需复杂控制,因此主要对升降翻转机构做分析与研究．

图1 新型混联式汽车电泳涂装输送机构Fig.1 Novel hybrid auto-mobile electro-coatingconveying mechanism

翻转升降机构笛卡尔空间动力学方程如下：

(1)

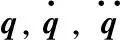
式(1)构建的机构动力学方程包含如下性质

(1)M对称并且为正定矩阵,即

MT=M，uTMu>0,∀u∈Rn,u≠0

式(1)所构建的是以工作空间即连接杆中点位姿信息q=(x,z,β)T为广义坐标建立的标准动力学方程,而实际控制量为各主动关节的力/力矩,为便于运算需将动力学模型方程从任务空间转换到关节空间．

将车身翻转升降机构动力学方程的相关参数由工作空间变换到关节空间的关系为：

(2)

升降翻转机构在关节空间中的动力学方程为：

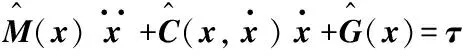
(3)

式中:τ为机构关节实际控制需要的驱动力/力矩．

图2 升降反转机构简图Fig.2 Structure of the lifting and turning mechanism

混联机构在控制中受到传感器噪声、测量误差、未建模动态、关节摩擦力、负载变化、槽液扰动等不确定性因素影响,若在建模时不考虑这些不确定量,会降低控制器的性能甚至造成系统不稳定．为使建立的动力学模型与实际相符,构建含建模误差ΔM、ΔC、ΔG、摩擦力f(x)和外界随机扰动τext的升降翻转机构动力学模型：

(4)

(5)

式(5)中τd受客观条件限制无法精确建模,为不确定项,因此需对其进行逼近和补偿．

2 极限学习机

混联式汽车电泳涂装输送机构运行时摩擦力、槽液阻力和外界随机扰动会影响电泳涂装质量,神经网络因其强大逼近能力,可以很好地对未知不确定量进行逼近和补偿,但在多车型共线柔性化生产时神经网络参数需要频繁调整,加大了柔性化生产难度．文献[16-17]提出ELM，相较于传统单隐层神经网络,不仅具有优良的泛化性能,网络训练速度也获得极大提升,同时能避免易陷入局部极小、过多迭代次数、训练耗时过长等基于梯度下降的前馈神经网络导致的问题,更为重要的是ELM无需大量参数的调节整定,既能降低网络准备时间和难度,同时还可以保证模型精度和泛化性能．

i,j=1,2,…,N

(6)

式(6)可简化为：

Hβ=T

(7)

式中：

(8)

(9)

式中：H为SLFN的隐层输出矩阵;第i列参数为与输入值x1,x2,…,xN有关的第i个隐层神经元的输出向量;第j行参数为与输入值xj有关的隐层神经元输出向量．由文献[13]可得以下定理:

(1) 一个任意无限可微的激活函数G:R→R,对于包含隐含层神经元的SLFN,在ai,bi的值随机选取的情况下,其隐层神经元输出矩阵H可逆且有‖Hβ-T′‖=0．

由定理(1)可推得,对于随机选取的ai和bi,若隐层神经元与训练集样本具有相同个数,那么SLFN便能以零误差的精度逼近训练样本,即：

(10)

(11)

(12)

(13)

由式(13)得输出权值为：

(14)

式中：H†为隐含层输出矩阵H的广义逆．

3 控制器设计

文中采用反步法进行控制器设计,然后针对系统中存在的不确定量,采用ELM进行逼近和补偿,以消除混联输送机构模型中不确定量的影响,并用Lyapunov稳定性方法保证系统稳定，控制系统结构如图3．

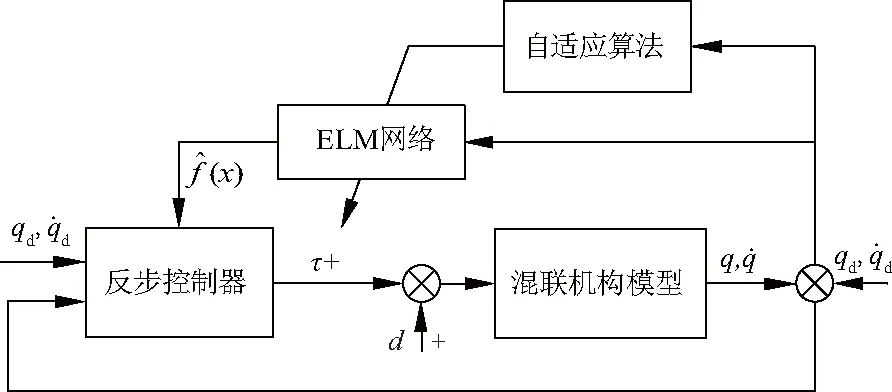
图3 混联机构自适应反步控制系统Fig.3 Adaptive control system for hybrid mechanism

3.1 反步控制器设计

第1步 设yd为期望位置指令,且yd具有二阶导数．

定义误差为:

z1=y-yd

(15)

取虚拟控制量:

(16)

式中：λ1>0．

定义误差:

z2=x2-α1

(17)

则:

(18)

针对第一个子系统,设计Lyapunov函数为:

(19)

则:

(20)

第2步 由式(18)求导得:

(21)

针对第二个子系统,设计Lyapunov函数为：

(22)

则

(23)

(24)

(25)

3.2 ELM逼近

集总扰动τd包含混联输送机构运行中的摩擦力、建模误差和外界随机扰动等不确定量,为了保证系统稳定并消除扰动影响实现精确控制,采用ELM逼近τd．

输入向量z=(z1z2)T,则有：

(26)

τ(z)d=β*Th(z)+ε

(27)

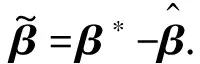
设计Lyapunov函数为：

(28)

对其求导,得：

(29)

式中：γ>0,ζ=[z1z2]T．

设计神经网络权值自适应律为:

(30)

式中：k1>0．

(31)

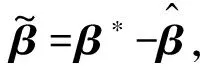
(32)

假定神经网络最大逼近误差及理想权值均有界,即‖ε‖≤εmax,‖β‖F≤βmax,εmax与βmax均为正常数．

根据Schwarz不等式,可得：

(33)

(34)

(35)

若式(35)成立,则：

(36)

(37)

4 仿真研究

为了验证文中设计的基于ELM的自适应反步控制器的有效性,以翻转升降机构为控制对象,考虑建模误差、摩擦力和外界随机扰动等不确定量,采用MATLAB进行仿真实验,同时为显示其控制效果,选用RBF自适应反步控制器作为对比．

根据文献[18],设粘性系数Bc与库伦摩擦力Fc为：

Bc=diag(0.7,0.7,0.7,0.7,0.9,0.9)
Fc=diag(3.5,3.5,3.5,3.5,4.1,4.1)

(38)

根据文献[19],外部干扰和建模误差分别设为：

(39)

ΔM=0.2×M,ΔC=0.2×C,ΔG=0.2×G

(40)

翻转升降机构连接杆中点的期望轨迹为:

(41)

(42)

各关节初始位置为：

x=(0.42,-0.42,0.42,-0.42,0.1,0.1)

(43)

ELM网络输入为z=(z1z2)T,采用Sigmoid函数作为激活函数．经由对比调试,选取网络隐层神经元数m=12,网络输入层到隐层神经元权值I取0～1中随机数,网络输入阈值b取200～300中随机数,隐含层到输出层权值估计值初始化为0.1．系统控制器参数选取λ1=7,λ2=1 000,k1=0.001,γ=100,εmax=0.1．

RBF网络隐层神经元数同为m=12,高斯基函数参数中心矢量值选取范围为[-1,1],基宽度为20,隐含层到输出层权值估计值初始化为0.1．

翻转升降机构的第一滑块与第三滑块对称,第二滑块与第四滑块对称,第一主动轮与第二主动轮对称,因此仅给出第一滑块、第二滑块和第一主动轮的仿真研究图．图4～6分别为给定轨迹下,包含模型不确定量及存在外部扰动的情况,第一、第二滑块和第一主动轮的轨迹跟踪曲线，Ref为给定参考轨迹,可以看出基于ELM的自适应反步控制的轨迹跟踪曲线在存在较大扰动的情况下收敛更快,实现了对期望轨迹的精确稳定跟踪,轨迹跟踪性能优于基于RBF的自适应反步控制．

表1 混联式汽车电泳涂装输送机的动力学参数Table 1 Dynamic parameters of the novel hybridautomobile electro-coating conveying mechanism

图4 第一滑块轨迹跟踪曲线Fig.4 Trajectory of the first slider

图5 第二滑块轨迹跟踪曲线Fig.5 Trajectory of the second slider

图6 第一主动轮轨迹跟踪曲线Fig.6 Trajectory of the first active wheel

图7～9给出第一滑块、第二滑块和第一主动轮的轨迹跟踪误差,可以看出基于RBF的自适应反步控制在外部扰动的影响下存在较大跟踪误差,而基于ELM的自适应反步控制跟踪效果更优,误差更小．表2列出两种控制方法轨迹跟踪误差的均方根误差(root mean squre error，RMSE),从中可以看出基于ELM的自适应反步控制器的RSME同样小于基于RBF的自适应反步控制器的RSME,说明所提出的控制方法具有更好的轨迹跟踪控制性能．

图7 第一滑块轨迹跟踪误差Fig.7 Tracking error of the first slider

图8 第二滑块轨迹跟踪误差Fig.8 Tracking error of the second slider

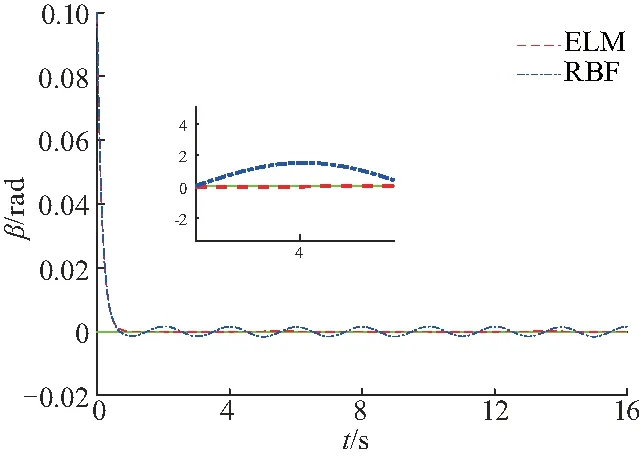
图9 第一主动轮轨迹跟踪误差Fig.9 Tracking error of the first active wheel

表2 不同控制方法跟踪效果比较Table 2 Comparison of performance index ofdifferentcontrol methods

为进一步研究所设计控制器对扰动的估计能力,图10～12给出ELM及RBF对各关节扰动量的估计误差,从中可以得出,ELM对各关节扰动量的估计误差皆小于RBF,说明其在线估计扰动能力更强．基于以上实验结果可得出,得益于ELM的高速调节能力,混联机构轨迹跟踪收敛速度更快,跟踪误差更小;又因ELM网络参数随机选取,减少了控制器准备时间和复杂性,同时具有较好的泛化性能．因此,基于ELM的自适应反步控制与基于RBF的同类控制方法相比,其跟踪精度更高,鲁棒性更强．

图10 第一滑块扰动估计误差Fig.10 Disturbance estimated error of the first slider

图11 第二滑块扰动估计误差Fig.11 Disturbance estimated error of the second slider

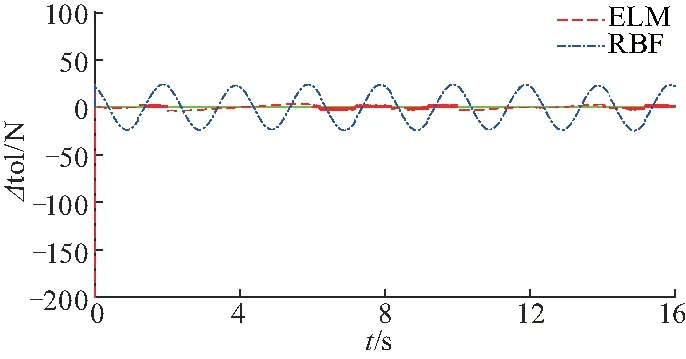
图12 第一主动轮扰动估计误差Fig.12 Disturbance estimated error ofthe first active wheel

5 结论

(1) 针对混联机构控制中的复杂非线性问题,基于自适应反步控制方法,分阶逐步设计反步控制器,有效降低了控制系统的设计复杂度．

(2) 将机构动力学建模误差、摩擦力、槽液阻力与其他未知外部扰动等作为集总干扰项,利用ELM网络强大的非线性逼近能力进行在线逼近,通过权值自适应率对ELM网络的输出进行在线调整,并补偿控制器输出,有效抑制了未知干扰对机构运行的影响,提升了混联机构轨迹跟踪控制性能与鲁棒性．

(3) 将反步法与ELM网络相结合,降低系统复杂度同时提升控制精度,与传统智能控制方法相比,减少了神经网络计算量并提升执行速度,可实际应用于混联机构轨迹跟踪的动力学控制．仿真结果表明,使用该方法作为混联机构控制,可以有效消减扰动影响,极大降低了系统的动态误差．

后续将进一步研究提高混联输送机构控制性能的方法,着重解决混联机构控制系统中的存在的不匹配干扰问题．