基于证据推理的气体体积分数变化问题分析
湖南 左传鹏
在多年的高三教学中,笔者发现学生在分析化学平衡中的体积分数问题时,经常会认为:化学平衡正向移动,反应物的体积分数必然减小,生成物的体积分数一定增大。事实真的是这样的吗?注重“证据推理”和“模型认知”是培养学生化学学科核心素养的重要途径。笔者在教学时试着引导学生回归气体体积分数的概念,利用数学思维方法,建立模型理性推断,探讨了改变不同条件时,平衡移动引发气体体积分数的变化规律。
一、体积分数的概念
1.分体积
分体积是指在相同温度下,当某一组分气体的压力为混合气体的总压时所单独占有的体积。该关系也叫阿马格分体积定律。
2.体积分数
在与混合气体相同温度和压强的条件下,混合气体中组分B单独占有的体积(即分体积VB)与混合气体总体积(V总)之比,叫做组分B的体积分数,用符号φ(B)表示,即
不难发现,组分B的体积分数在数值上等于组分B在混合气体中所占的物质的量分数。
二、体积分数变化情况探讨
1.改变平衡体系的温度或压强

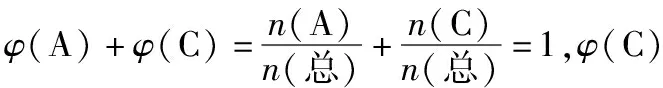
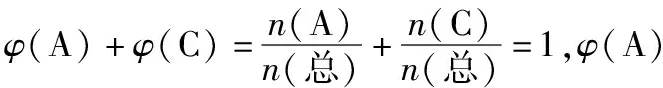
可见,对于反应物和生成物各只有一种的可逆反应,当平衡正向移动,反应物的体积分数一定减小,生成物的体积分数一定增大。对于反应物或生成物不唯一的可逆反应,当平衡正向移动,能否得出相同结论呢?

(1)当m+n 设原平衡时A、B、C和D的物质的量分别为amol、bmol、cmol和dmol,其他条件不变,改变温度(或容器体积),使平衡右移,A减少了mxmol。 原平衡molabcd 转化molmxnxpxqx 新平衡mola-mxb-nxc+pxd+qx 作差比较可得: φ′(C)-φ(C) 由于a+b+c+d>c,且m+n ①当p≥p+q-m-n,即组分C的化学计量数大于或等于反应前后气体化学计量数之差时,φ′(C)-φ(C)>0,C的体积分数增大; ②当p (2)当m+n>p+q。达到平衡后,其他条件不变,改变温度(或容器体积),使平衡正向移动,则n(A)减小,n(B)减小,n(C)增大,n(D)增大,n(总)减小,故φ(C)和φ(D)均增大,根据体积分数和为1,[φ(A)+φ(B)]之和必然减小,φ(A)和φ(B)是否都减小呢? 同理可证: φ′(A)-φ(A) 由于a+b+c+d>a,且m+n>p+q,故: ①当m≥m+n-p-q,即组分A的化学计量数大于或等于反应前后气体化学计量数之差时,φ′(A)-φ(A)<0,A的体积分数减小; ②当m 综上,当其他条件不变,只改变容器体积(或温度)时,平衡发生移动。对于反应物和生成物各只有一种的可逆反应,反应物的体积分数一定减小,生成物的体积分数一定增大;而对于反应物或生成物不唯一的可逆反应,当某一气体的物质的量和体系内所有气体的总物质的量同增或同减时,该气体的体积分数变化情况需通过计算才能判断。 以上分析的是只改变温度或压强,平衡移动后各气体组分体积分数的变化情况。如果在恒容条件下改变平衡体系中组分的浓度,平衡移动后,各组分的体积分数又将会如何变化呢? 2.改变反应物的浓度 (1)按原投料比追加投料 【答案】不能确定 减小 增大 【解析】恒温恒容达到平衡后,再充入amol N2和bmol H2,平衡右移,n(N2)、n(H2)、n(NH3)及n(总)均增大,根据定义难以直接比较原平衡(如图Ⅰ建立的平衡状态)和新平衡(如图Ⅲ建立的平衡状态)体积分数的大小关系。可先虚拟一个中间状态Ⅱ,Ⅰ与Ⅱ两平衡状态等效,平衡时各组分体积分数对应相等。 “压缩”平衡状态Ⅱ,得到平衡状态Ⅲ,Ⅱ与Ⅲ中起始投料量相同,减小体积,观察该化学反应方程式中气体化学计量数,利用上文得出的压强改变时的体积分数变化规律,可做出判断:与原平衡相比,φ(N2)的变化不能确定,φ(H2)减小,φ(NH3)增大。 恒温恒容情况下,对于多反应物可逆反应或单一反应物可逆反应,如果按原投料比例追加投料,平衡移动后,各组分的体积分数变化可以通过虚拟中间状态来分析。 (2)改变某种反应物的浓度 恒温恒容情况下,对于多反应物可逆反应,如果只改变某一种反应物的浓度,平衡移动后,气体体积分数变化可以借助化学平衡常数加以分析。 【答案】增大 减小 不能确定 【解析】恒容通入N2,平衡右移,新平衡与原平衡相比,n(N2)增大,n(H2)减小,n(NH3)增大,n(总)变化不能确定,利用体积分数的概念难以作判断。不妨借助平衡常数来探讨: 【答案】减小 由此可见,恒温恒容情况下,对于含多气体反应物的可逆反应,只增大某一气体反应物的浓度,再次达平衡后的气体体积分数可借助化学平衡常数分析,当题中涉及具体量,可通过数学计算或利用极限法作出判断。 气体体积分数是一个比值定义,它与该组分气体的物质的量及体系内所有气体的总物质的量两个量有关,当平衡移动导致这两个量同增或同减时,该组分气体的体积分数将可能增大、可能减小,也可能不变,如果在教学中对其变化情况只作定性分析的话是无法使学生信服的。作为高中化学核心素养的组成要素之一,“证据推理与模型认知”的内涵体现在通过分析、推理等方法认识研究对象的本质特征、构成要素及其相互关系,建立模型并运用模型,揭示反应的本质和规律。因此,面对高三化学反应原理复习中类似问题,化学教师在传授化学基础知识和培养化学思维的同时,搭建平台,注重“证据推理”和“模型认知”,激发学生潜能,引导学生树立独立思考的习惯,培养学生用数学思维方法解决化学问题的意识和能力,提升严谨求实的科学品质,促进学生建立质和量统一的哲学观,这对学生的终身发展意义深远。
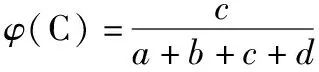
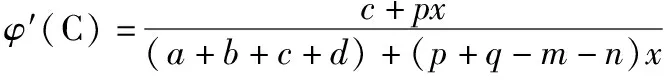

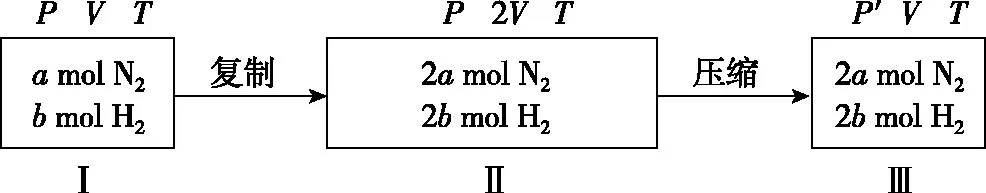



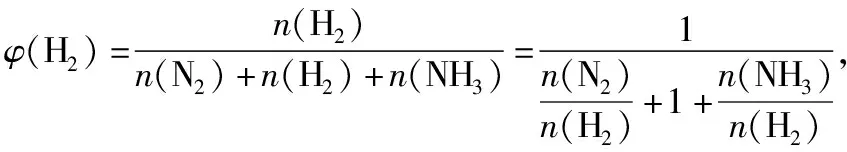
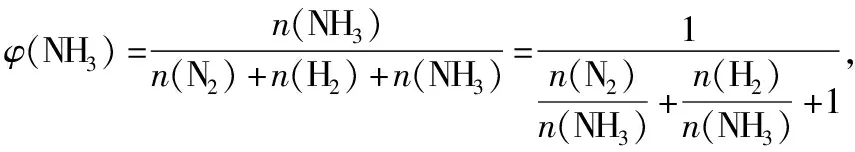
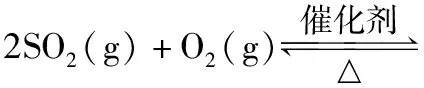
三、结语

