基于PDR和磁场匹配的智能手机室内定位
曹 峻,余科根,文 铠
(1.中国矿业大学环境与测绘学院,徐州 221116; 2.武汉大学测绘学院,武汉 430072)
0 引言
基于位置的服务(Location Based Services,LBS)为个人定位和导航等带来了极大的便利。智能手机内的惯性测量单元(Inertial Measurement Unit,IMU)可以为不同环境下的行人跟踪提供自主解决方案[1]。由于智能手机内置微机电系统的IMU通常精度较差,因此,使用行人航位推算(Pedestrian Dead Reckoning,PDR)方法生成磁场序列的轮廓特征。
地球磁场由于信息量丰富、可以实时方便匹配、精度高、稳定性好、成本低等,适合作为一种位置指纹来使用。基于磁场的室内定位存在以下问题[2]:1)目前使用的指纹采集方法普遍无法满足快速建库的要求,需要一种高效、可靠的室内磁性指纹数据库构建方法;2)与WIFI定位和蓝牙定位相比,地磁定位中由于智能移动设备的任意姿态,可用的磁场特征从原来的三维特征变为一维特征,匹配特征较少,如何快速进行匹配操作是研究难点。国内外基于惯性导航和地磁信息的室内定位技术研究中,文献[3]提出了基于磁约束的IMU定位算法,采用多级傅立叶变换方法提取特征,降低了轨迹累积误差且提高了精度;文献[4]则利用扩展Kalman滤波器(Extended Kalman Filter,EKF)融合不同类型的数据,提出了精确区分姿态相位的聚类算法,采用零速更新方法最小化积分误差。
本文IMU的输出可用于设置惯性导航系统(Inertial Navigation System,INS)机械编排并检测运动步数,如果步伐检测成功,则执行步长估计来计算当前步长和行人的步行速度。基于INS的PDR通过分别积分来自陀螺仪和加速度计的角速度和比力计算用户的位置[5]。该方法使用估计的步长和估算的航向产生移动速度更新和位置增量更新,以改善PDR导航性能。前进速度作为INS的速度更新,而位置增量则作为INS的位置更新,以改进位置和航向精度。磁力计的测量结果与来自INS的轨迹轮廓相结合,被输入到数据缓冲区中以设置磁场序列(Magnetic Field Sequence,MFS)[6]。如果磁场数据的缓冲长度超过预设阈值,则对测量MFS进行重新采样,并使用高斯牛顿迭代法在磁场图中找到与测量MFS具有最高相似性的参考MFS;如果地磁匹配定位算法成功,则参考MFS的位置将用作位置更新,以控制INS的导航误差并提高轨迹轮廓的准确性[7]。本文提出的C-INS方法可以很好地解决基于智能手机的PDR中未对准角度估计的问题。
1 捷联惯性导航系统力学编排
1.1 捷联惯性导航系统流程
通过载体坐标系(简称b系)和导航坐标系(简称n系)描述载体的运动状态。在进入解算前,先确立n系和b系的对应关系,实现载体运动状态从b系向n系的转换。在初始对准中,由于MEMS-IMU内置移动设备的陀螺精度较低,因此利用加速度计的输出计算俯仰角和横滚角,磁力计输出的磁场强度计算航向角[8]。IMU的漂移误差模型可采用一阶马尔科夫误差模型,修正b系下的陀螺仪和加速度计的原始误差[9],测得载体相对惯性空间的角速度和比力数据;再通过解算常微分方程组,对加速度计和陀螺仪提供的加速度和角速度数据进行多次积分,根据n系下的速度和时间间隔累计求得运动载体在n系中的姿态、位置及速度信息。
1.2 捷联惯性导航系统力学编排
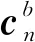
(1)
式中
(2)
由式(2)可以看出,当姿态角已知并给定初值后即可求解。考虑到载体的姿态变化快,利用四元数法表示b系相对n系的转动,进行姿态解算
Q=q0+q1ib+q2jb+q3kb
(3)
式中,ib、jb、kb与b系的基底相同。
其微分方程为
(4)
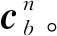
(5)
当载体和地球有相对运动时,加速度计计算的比力方程如下
(6)
式中,f为加速度计的数据值;ven表示载体和地球间的相对运动速度;wen×ven表示载体在地球表面运动时形成的向心加速度; 2wie×ven表示哥式加速度的数值。
因加速计测量值实际是沿b系的,所以要转换到n系下[11]。设加速度计的输出比力为
fb=[fx,fy,fz]T
(7)
则
(8)
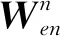
(9)
(10)
导航坐标系(即n帧)中离散INS机械编排算法方程的简化形式为
(11)
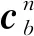
2 C-INS算法和EKF模型
2.1 C-INS算法设计
为了满足行人导航应用的需要,将步态模型中的前向行走速度和运动约束作为三维速度更新和二维位置增量应用,以提高惯性导航系统的速度[12],称为C-INS。
n帧中速度观测方程由式(12)给出
(12)

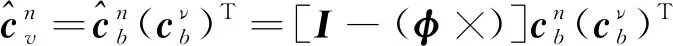
(13)
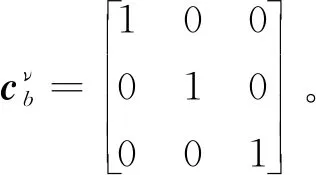
(14)
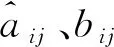
(15)
航向角即为
(16)
式中
c32φy)+b13(c13+c23φZ-c33φy)
(17)
c12φZ)+b13(c23+c33φX-c13φZ)
(18)
n帧中的航向观测方程由式(19)给出
(19)
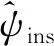
(20)
(21)
(22)
2.2 EKF系统模型和多级测量方程
使用基于INS的PDR具有更高的输出频率,可以提供相对轨迹轮廓替代方案,以改善磁场指纹的辨别力。陀螺仪和加速度计的测量值积分后会导致位置误差,为此,基于IMU的误差模型,在n系中利用速度误差矢量、姿态误差角矢量以及位置误差矢量,使用EKF融合多源观测量进行滤波和状态估计,继而修正系统误差。所提出的方法中状态变量定义如下[13]
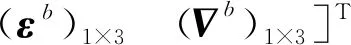
(23)
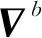
δxk|k-1=φk-1δxk-1|k-1+wkδzk=Hkδxk|k-1+vk
(24)
式中,δxk-1|k-1、δxk|k-1代表先前的误差状态向量和预测的误差状态向量,下标k-1和k代表时期;δzk代表测量误差矢量;wk代表过程噪声;Hk代表设计矩阵;vk代表测量噪声;φk-1是15×15的量测矩阵,表示为
(25)
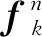
2.3 磁场匹配定位
1)离线阶段
为确保磁力计的输出真实反映周围环境的磁场,必须在使用磁力计感知磁场之前,利用开发的安卓应用程序执行传感器校准过程。在离线数据收集阶段,使用INS机械编排产生的横滚角和俯仰角获得磁场强度的水平和垂直分量[14]。已知点(Known Points,KPs)的坐标和在KPs处的磁场观测是影响磁场图精度的2个主要因素。为了平衡制图精度、效率和人工成本,利用步行测量方法(WS)沿着与房间的x轴平行的线或与y轴平行的线收集磁场数据,以提高构建磁场图的工作效率[15]。使用由许多直线组成的路径以确保KPs的测量密度,同时利用稀疏的具有已知坐标的点和恒定的行走速度进行约束,记下经过每个指定点的时间,并在测试期间将它们写入文件,此外,在高精度地图上选择相应的点来获得上述点的坐标。最后,通过时间线性插值计算出相邻指定点之间的KPs坐标,生成分辨率为0.2m的栅格磁场图。其中,Gi代表拐角点或支柱点,KPi代表KP位置,FMi={Pi,Mi}代表KP的磁场指纹。G1和G2之间的KPi坐标计算公式如下,其中T表示经过路点的时间。
(26)
2) 在线定位阶段
在线匹配时,最多3个分量不足以实现磁场指纹的精确匹配定位,使用历史磁场数据和相应的相对坐标来构造MFS,如下
(27)
式中,k代表磁场数据的长度,而i是MFS的纪元。使用高斯牛顿迭代法执行磁场轮廓匹配定位[16],该算法不需要在磁场图中遍历一个固定的区域,可以根据磁场梯度快速找到最优的转换参数。
假定刚性变换为
ε=[px0,py0,Δφ]T
(28)

(29)
地磁匹配定位算法在n帧中的定位结果的误差由式(30)给出
(30)
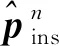
3 实验结果分析
3.1 地磁匹配定位算法实验结果
为了评估所提出的室内定位算法的性能,实验人员在武汉大学珞珈创意园16楼遵循预定轨迹进行了实验。轨迹位于典型的室内办公楼环境(约300m2)中,走廊狭窄。实验人员手持小米8智能手机按标红路线走动,并将智能手机保持在距离地面约1.2m的高度。智能手机的前进方向和参与者的步行方向之间角度差小于10°。
1)磁场图
利用磁场序列与轨迹相结合的方法,构造了一种新的磁场特征以实现更好的磁场匹配。智能手机的内置磁力计具有很高的采样率,并且行人的正常步行速度通常约为1.2m/s。所以在在线定位阶段可以用较低的计算成本,重新采样所收集的磁场数据以生成稀疏的MFS。在本文中,使用长度为10m的MFS进行位置估计。如图1所示,磁场强度在0.2m范围内的变化可以忽略不计。与动态时间规整(Dynamic Time Warping,DTW)[8,13]算法相比,该算法使用了网格磁场图,因此对用户行走轨迹不敏感,而且结合来自PDR的轨迹轮廓具有更高的磁场指纹识别能力。该算法与基于粒子滤波(Particle Filter,PF)的定位算法精度接近,但计算复杂度低、收敛速度快。
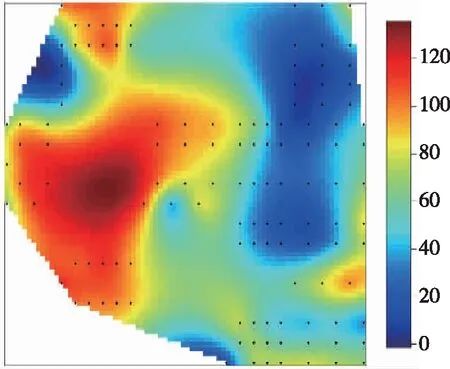
图1 磁场强度基准图Fig.1 Reference diagram of magnetic field intensity
2)位置估算效果分析
在试验区域进行了实验轨迹测试,位置估计结果如图2所示,累积误差百分比(Cumulative Error Percentages,CEPs)如图3所示。图2中,红色、蓝色、绿色和紫色实线分别表示参考轨迹、INS、MM和MM/INS的位置轨迹。对于CEP图形,天蓝色、绿色和蓝色线分别表示INS、MM和MM/INS。MM和MM/INS集成方法通过使用基于INS的PDR的轨迹轮廓改善MFS的识别。
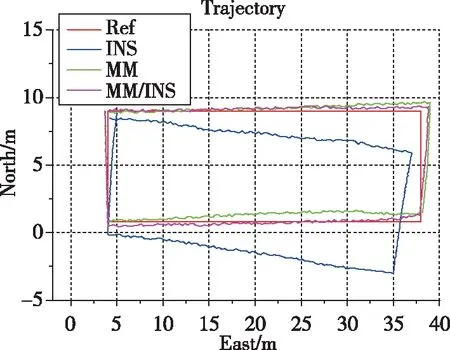
图2 位置估计结果Fig.2 Result of position estimation

图3 累积误差百分比(CEPs)Fig.3 Cumulative error percentage (CEPs)
所提出的MM算法可以在走廊环境中实现高精度的位置估计,测试的INS、MM、MM/INS集成方法的位置误差如表1所示。基于MEMS-IMU的INS解决方案的均方根(Root Mean Square,RMS)位置误差为3.65m。
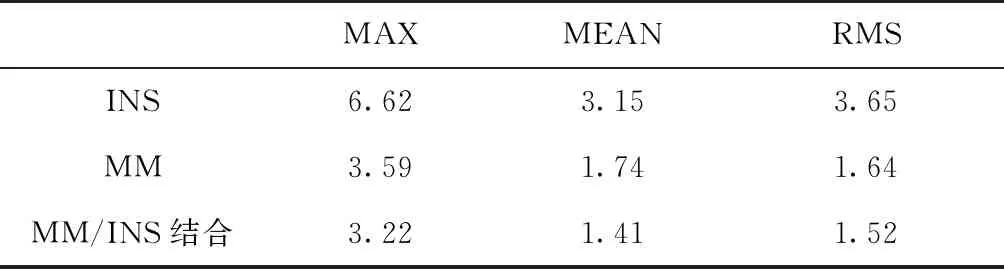
表1 测试实验中的位置误差
所提出的基于磁场指纹的MM解决方案在测试中的RMS位置误差为1.64m,而匹配成功率为95.19%。匹配成功率指的是成功匹配的总数除以匹配的总数。集成解决方案的RMS位置误差为1.52m。根据测试的结果,提出的MM算法具有良好的位置估计性能和较高的匹配成功率。
3.2 C-INS实验结果
实验环节设计了步行测试,并分析了所提出的C-INS算法与现有的E-PDR算法在手持设备、打电话模式和放在裤子口袋中3个基本位置的位置估计和航向估计方面的性能。
1)C-INS和E-PDR方法之间的航向估计
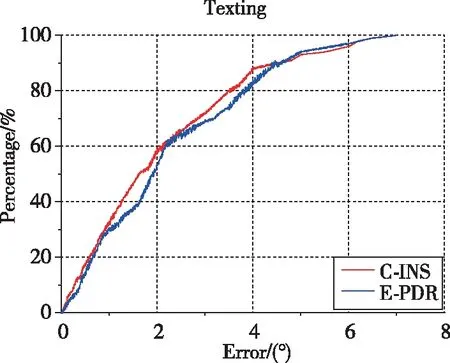
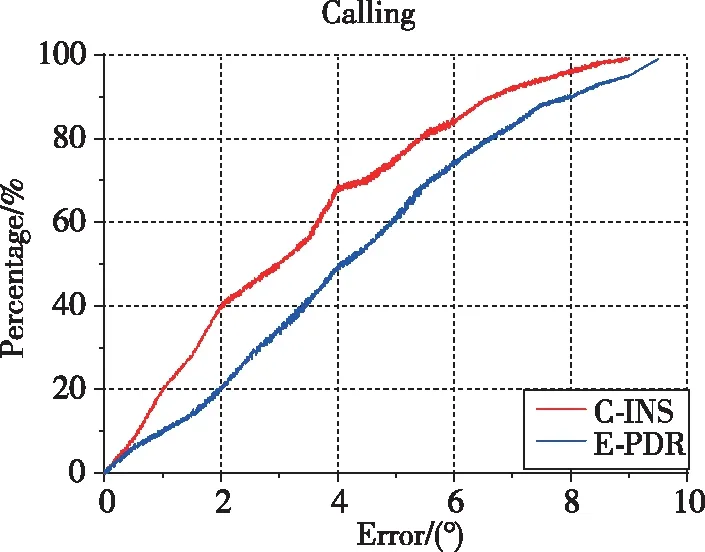
表2说明了这两种算法在3个位置具有一致的统计航向性能。E-PDR方法的RMS航向误差保持位置分别为3.43°、6.22°和17.65°,而C-INS方法的保持位置分别为3.74°、6.52°和16.86°。C-INS方法因使用步态模型获得了更好的航向估计。图4所示为相应的航向累积误差百分比图。
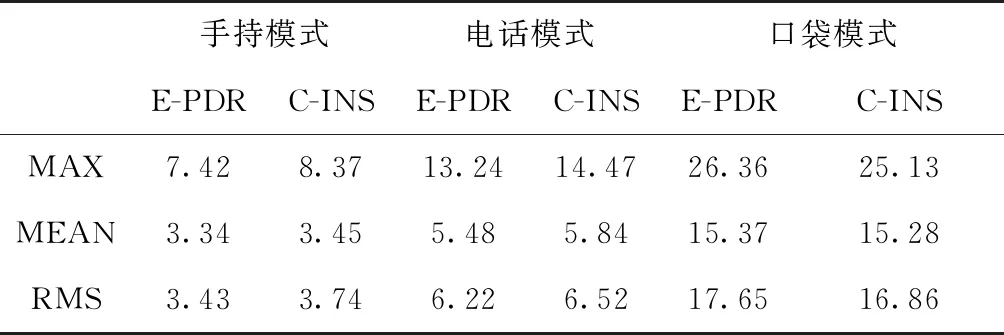
表2 E-PDR和C-INS在不同位置的航向角误差
2)C-INS和E-PDR方法之间的位置估计
图5和图6显示了C-INS和E-PDR解决方案实验中,3个位置的估计结果和位置累积误差百分比。红色、绿色和蓝色实线分别表示参考轨迹、C-INS方法的轨迹和E-PDR方法的轨迹。E-PDR方法在不同位置的统计定位误差分别为2.15m、1.94m和1.73m,C-INS方法的统计定位误差分别为1.15m、1.84m和1.73m,如表3所示。因C-INS方法使用步态模型来提高滚转角和俯仰角的精度,故在位置估计方面表现出了更好的性能。
(a)手持模式
(b)电话模式
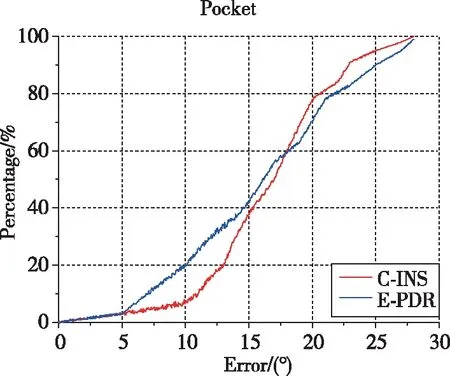
(c)口袋模式图4 航向角累积误差百分比Fig.4 Cumulative error percentage of heading
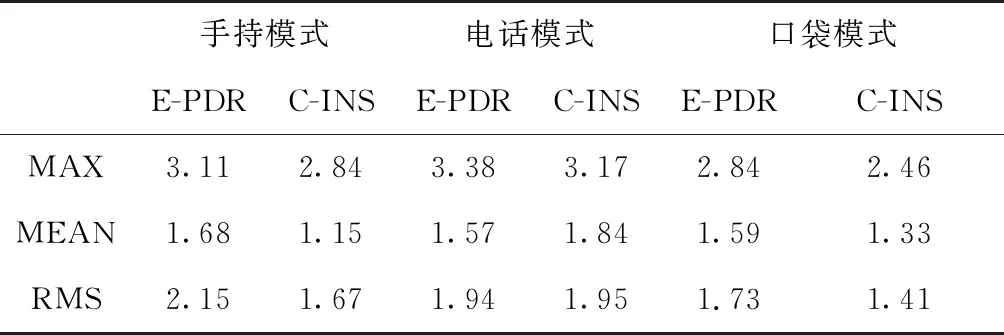
表3 E-PDR和C-INS解决方案在3个不同 电话保持位置的定位误差
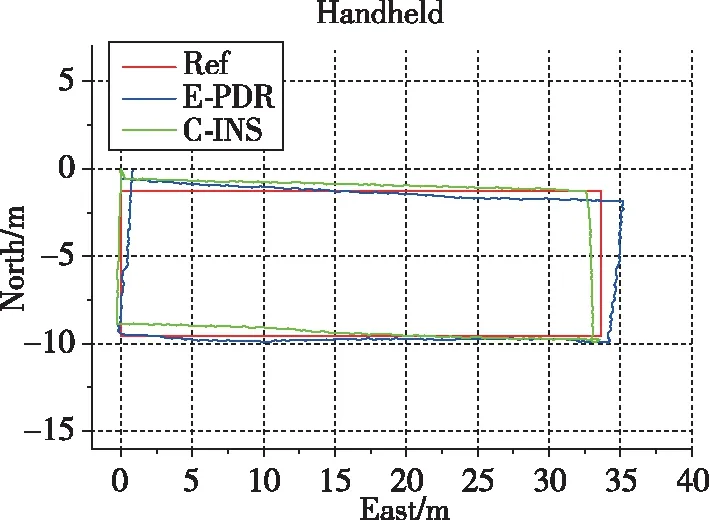
(a)手持模式
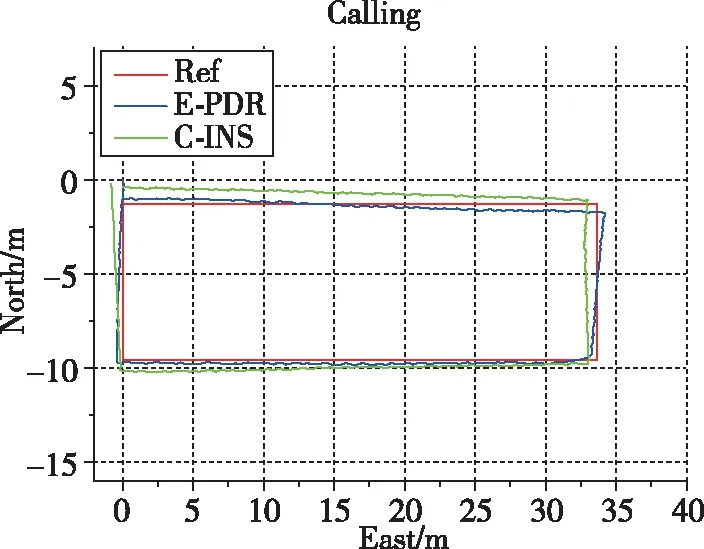
(b) 电话模式

(c) 口袋模式图5 E-PDR和C-INS在3个位置的估计结果Fig.5 Estimation results of two methods in three positions
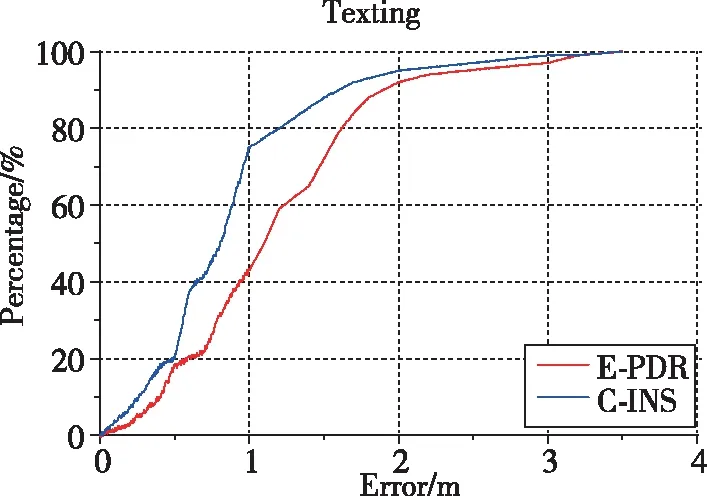
(a)手持模式
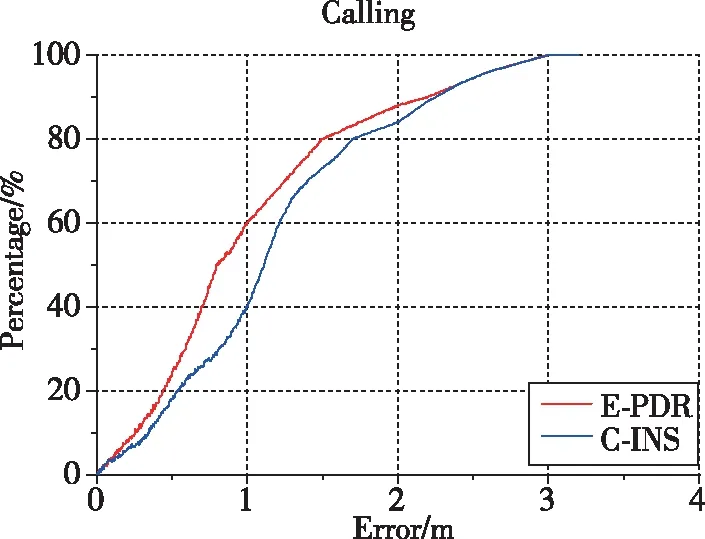
(b) 电话模式
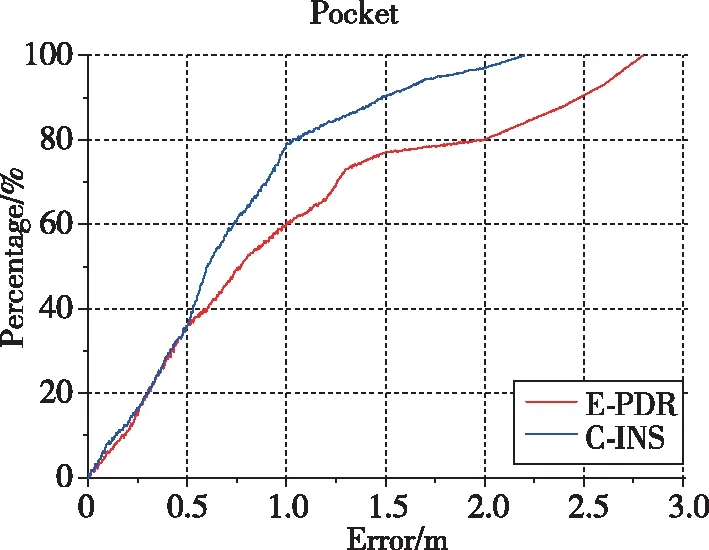
(c) 口袋模式图6 E-PDR和C-INS在3个位置的累积误差百分比Fig.6 Cumulative error percentage of E-PDR and C-INS in three positions
4 结论
1)基于环境磁场图的匹配定位方法,提高了磁场匹配定位的位置估计精度。将磁场序列与来自基于INS的PDR的估计轨迹结合使用,提高了磁场指纹的可分辨性,并设计了高斯牛顿迭代法进行磁场轮廓匹配定位。
2)基于智能手机内置传感器,利用步态模型和运动约束提供伪测量的C-INS方法,提供了更高频率的输出、更丰富的三维速度信息,以及更可靠的位置估计和航向估计。实际的步行测试证明了利用C-INS方法可以很好地解决基于智能手机的PDR中未对准角度估计的问题。

