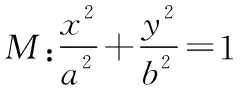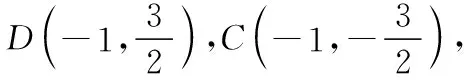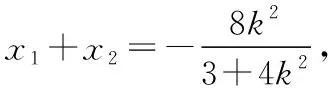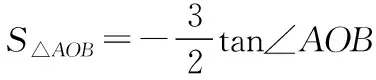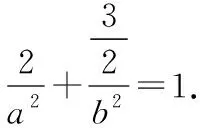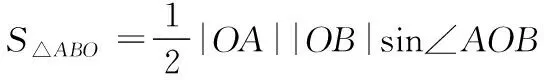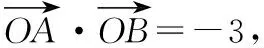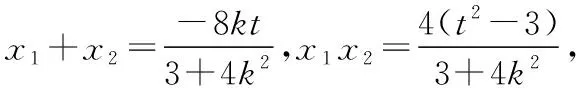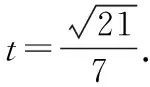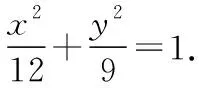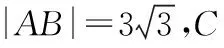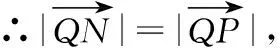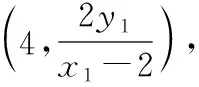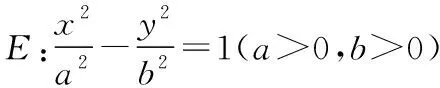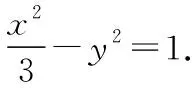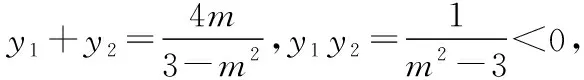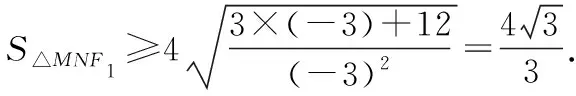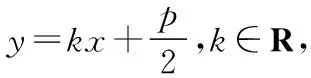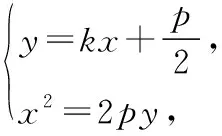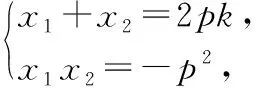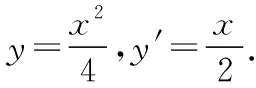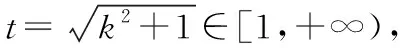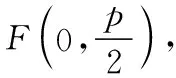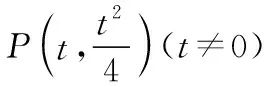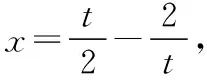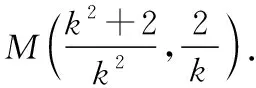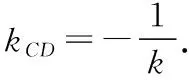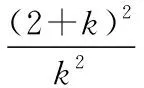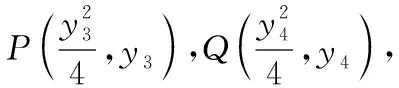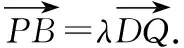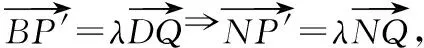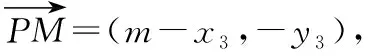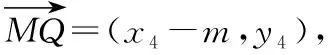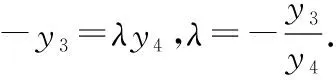教学考试杂志社“优师计划”阶段性成果展示——高考重难点相关试题选登

( )

A.10 B.12

C.15 D.20

【答案】B

( )

【答案】C

( )

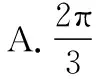
【答案】B

( )

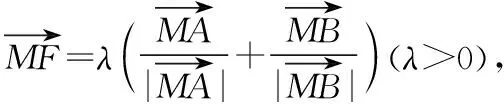
【答案】C

( )

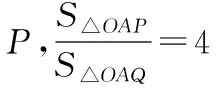
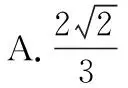
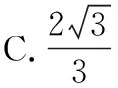
【答案】C

( )

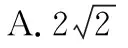
【答案】D

( )

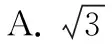
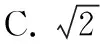
【答案】A

( )

【答案】A

( )

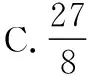
【答案】B

( )

【答案】B

11.【细磨题】(本小题满分12分)

(Ⅰ)求椭圆C的方程；

(Ⅱ)斜率为1的直线l交椭圆C于M(x1,y1),N(x2,y2)两点,且x1>x2.若直线x=3上存在点P,使得△PMN是以∠PMN为顶角的等腰直角三角形,求直线l的方程.

【考查角度】本题考查直线与椭圆的位置关系,考查化归与转化思想和运算求解能力，考查逻辑推理、数学抽象、数学运算等核心素养.(Ⅰ)由已知两点在椭圆上,代入椭圆的标准方程可求出a,b的值；(Ⅱ)联立直线与椭圆方程，确定m的范围并找出x1，x2的关系.易知NP平行于x轴，所以NP中点的横坐标就是点M的横坐标，进而列方程组求解.

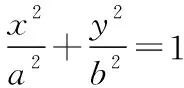
(3分)

解得a2=3,b2=1.

(5分)

(Ⅱ)设直线l的方程为y=x+m,P(3,yP),

(6分)

(7分)

由Δ=36m2-48m2+48>0,得-2

(8分)

因为△PMN是以∠PMN为顶角的等腰直角三角形,

所以NP平行于x轴.

(9分)

过点M做NP的垂线,则垂足点Q为线段NP的中点.

设点Q的坐标为(xQ,yQ),

(10分)

整理得m2+2m+1=0,解得m=-1.

(11分)

而m=-1∈(-2,2),

所以直线l的方程为y=x-1.

(12分)

12.【细磨题】(本小题满分12分)

(Ⅰ)求椭圆方程；

(Ⅱ)记△ABD与△ABC的面积分别为S1和S2,求|S1-S2|的最大值.

【考查角度】本题考查椭圆的定义、直线与椭圆的关系、均值不等式求最值，考查运算求解、逻辑推理能力，考查数学运算、数据分析、逻辑推理和数学建模的核心素养.

(Ⅰ)通过椭圆方程基本量a,c求解,借助通径,得方程,即可解得a,b,c的值，从而得椭圆方程;(Ⅱ)利用面积公式,直线与圆锥曲线位置关系联立方程,由韦达定理,运用面积公式,变形后由均值不等式求解即可.

又∵b4=(a+c)2(a-c)2=(a2-c2)2,

代入得c2=3或1,

又a>b>c>0,∴c=1,

又a2=4,∴b2=3,

(4分)

(Ⅱ)当直线l斜率不存在时,直线方程为x=-1,

△ABD,△ABC面积相等,|S1-S2|=0.

(5分)

当直线l斜率存在时(k≠0),

设C(x1,y1),D(x2,y2),

直线方程为y=k(x+1)(k≠0),

消掉y,得(3+4k2)x2+8k2x+4k2-12=0.

(7分)

此时|S1-S2|=2||y2|-|y1||=2|y2+y1|

=2|k(x2+1)+k(x1+1)|

=2|k(x2+x1)+2k|

(9分)

(11分)

(12分)

13.【细磨题】(本小题满分12分)

(Ⅰ)求椭圆的标准方程；

【考查角度】本题考查椭圆的标准方程、直线与椭圆的关系、数量积和三角形面积公式，考查运算求解能力与数形结合的数学思想,考查逻辑推理的核心素养.

【解题分析】(Ⅰ)设离心率为e,由题意知，

(1分)

所以a2=4,b2=3,

(2分)

(4分)

(Ⅱ)设M(0,t),直线l的方程为y=kx+t，

A(x1,y1),B(x2,y2)，

(5分)

所以|OA||OB|cos∠AOB=-3,

(7分)

联立直线l和椭圆C的方程，有

整理得(3+4k2)x2+8ktx+4t2-12=0，

Δ=(8kt)2-4×(3+4k2)×(4t2-12)

=48(4k2-t2+3)>0,

(8分)

因为x1x2+(kx1+t)(kx2+t)=-3,

所以(1+k2)x1x2+kt·(x1+x2)+t2=-3,

(9分)

4(k2t2-3k2+t2-3)-8k2t2+(4k2t2+12k2+3t2+9)=0,

(11分)

(12分)

【方法点拨】该题考查的是直线与椭圆相交的问题，在解题的过程中，一是需要掌握椭圆方程中对应的参数a,b,c之间的关系，再者联立直线方程与椭圆方程即"几何问题代数化"，应用韦达定理,把两个交点问题转变为方程两个根的问题.同时直线的方程在设的时候一定要注意斜率的存在与否问题，本题的关键是从题中寻找对应的等量关系.

14.【研发题】(本小题满分12分)

(Ⅰ)求曲线Γ的方程；

(Ⅱ)△ABC的面积是否为定值？若是,求出该定值;若不是,请说明理由.

【考查角度】本题考查椭圆的标准方程及性质、直线与椭圆的位置关系、韦达定理、弦长公式、三角形的重心的性质,考查转化思想,考查推理运算能力,考查数学抽象、数学运算核心素养.

(Ⅰ)根据题意列出方程并化简即可；(Ⅱ)要分斜率存在和斜率不存在两种情况来考虑,在表达三角形ABC的面积时,要求线段AB弦长,要求点C到AB的距离来表示三角形面积,属于常规圆锥曲线题.

【解题分析】(Ⅰ)设曲线Γ上的任意一点M的坐标为(x,y),

(5分)

(Ⅱ)当直线AB斜率不存在时,

(6分)

(7分)

当直线AB的斜率存在时,设直线AB方程为

y=kx+m,A(x1,y1),B(x2,y2),

得(3+4k2)x2+8kmx+4m2-36=0,

(8分)

(9分)

∵O为△ABC的重心,

∵C点在椭圆M上,

化简得4m2=12k2+9，

(12分)

15.【细磨题】(本小题满分12分)

(Ⅰ)求点Q的轨迹C的方程；

(Ⅱ)设曲线C的左、右顶点分别为A,B,E是C上异于A,B的任意一点,直线EN交C于另一点H,直线EB交直线x=4于点K,求证：A,H,K三点在同一条直线上.

【考查角度】本题考查椭圆的定义与标准方程、直线与椭圆的位置关系,考查运算求解能力与数形结合的思想,考查逻辑推理、数学运算的核心素养.

(2分)

由椭圆的定义可知，点Q的轨迹C是以点M，N为焦点，且长轴长为4的椭圆,

∴2a=4,c=1,b2=a2-c2=3，

(4分)

(Ⅱ)证明：设点E(x1,y1),H(x2,y2),

直线EH的方程为x=my+1,

整理得(3m2+4)y2+6my-9=0,

∵Δ=(6m)2+36(3m2+4)>0,

(7分)

将此方程与直线x=4联立,

(9分)

(11分)

故A,H,K三点在同一条直线上.

(12分)

【方法点拨】该题考查的是直线与椭圆相交的问题,在解题的过程中,一是需要掌握椭圆方程中对应的参数a,b,c之间的关系,再者联立直线方程与椭圆方程，即“几何问题代数化”,应用韦达定理,把两个交点问题转变为方程两个根的问题.同时，直线的方程在设的时候一定要注意斜率的存在与否问题,本题的关键是从题中寻找对应的等量关系.

16.【研发题】(本小题满分12分)

(Ⅰ)求双曲线E的方程；

(Ⅱ)过点F2作直线l与双曲线的右支交于M，N两点,求△MNF1的面积的取值范围.

【考查角度】本题考查双曲线的方程与性质、直线与双曲线的位置关系、弦长公式、面积的计算，考查数学运算能力、转化与化归能力.

(4分)

整理可得(m2-3)y2+4my+1=0,

设M(x1,y1),N(x2,y2),

所以m2-3<0,

(5分)

设m2-3=t,则-3≤t<0,

(12分)

17.【细磨题】(本小题满分12分)

过抛物线C:x2=2py(p>0)焦点的直线l与抛物线相交于A,B两点,点M为抛物线上任一点,且抛物线在点M处的切线与直线l平行,弦长|AB|的最小值为4.

(Ⅰ)求抛物线C的方程；

(Ⅱ)若△MAB的面积为S,求S+|AB|的最小值.

【考查角度】本题考查直线与抛物线的位置关系，考查化归与转化的思想和运算求解能力，考查逻辑推理、数学抽象、数学运算等核心素养.

(Ⅰ)先写出弦长的函数表达式,再根据弦长|AB|的最小值为4求得抛物线C的方程；(Ⅱ)写出S+|AB|的表达式,通过换元,利用导数研究S+|AB|的最小值.

(1分)

(2分)

Δ=4p2k2+4p2>0恒成立，

(3分)

(4分)

=k(x1+x2)+2p=2pk2+2p.

(5分)

因为k∈R,所以当且仅当k=0时,|AB|取得最小值,即2p=4,所以p=2,

所以抛物线C的方程为x2=4y.

(6分)

(7分)

因为抛物线在点M处的切线与直线l平行,

(8分)

由(Ⅰ)可知|AB|=4(k2+1),

(10分)

(11分)

则f′(t)=6t2+8t>0,

所以f(t)在[1,+∞)上单调递增，

所以f(t)min=f(1)=6,

故S+|AB|的最小值为6.

(12分)

18.【细磨题】(本小题满分12分)

(Ⅰ)求抛物线C的方程；

(Ⅱ)设P是抛物线C上任意一点,过点P作抛物线的切线交抛物线的准线于点Q,求证:PF⊥QF.

【考查角度】本题考查直线与抛物线相关知识,考查推理论证、运算求解能力,考查逻辑推理、数学运算等核心素养.

(Ⅰ)由条件写出直线AB的方程,与抛物线方程联立由韦达定理及中点坐标公式求得,也可直接利用点差法进行求解；(Ⅱ)设出点P坐标及切线方程,将切线方程与抛物线方程联立,由Δ=0得出斜率表达式,再求出Q点坐标,借助向量证明，也可利用导数及向量进行证明.

(1分)

整理得x2-2px-p2=0,

(2分)

解法一：设A,B横坐标分别为x1,x2,

则x1+x2=2p=4,p=2,

(4分)

所以抛物线C的方程是x2=4y.

(5分)

解法二：设A(x1,y1),B(x2,y2),

由题意知x1+x2=4,x2-x1=y2-y1, (*)

(1分)

因为点A,B均在抛物线C上,

(2分)

即(x2+x1)(x2-x1)=2p(y2-y1),

把(*)代入得p=2,

(4分)

所以抛物线C的方程是x2=4y.

(5分)

把切线方程代入抛物线方程得x2-4kx+4kt-t2=0,

(6分)

所以抛物线x2=4y在点P处的切线方程为

(8分)

抛物线x2=4y的准线方程是y=-1,

(9分)

又F(0,1)，

(10分)

(11分)

所以PF⊥QF.

(12分)

(6分)

(8分)

因为抛物线C的准线方程为y=-1,

(9分)

又F(0,1)，

(10分)

(11分)

所以PF⊥QF.

(12分)

19.【细磨题】(本小题满分12分)

(Ⅰ)求抛物线的方程;

(Ⅱ)求证：直线MN恒过定点．

【考查角度】本题考查抛物线标准方程及直线与抛物线的位置关系的应用与掌握程度，探求直线经过定点，考查考生的分析能力、计算能力，考查分类讨论,变量转换等数学核心素养.

【名师指导】(Ⅰ)由椭圆焦点即可得抛物线的p值；(Ⅱ)直线与抛物线联立，利用韦达定理和中点坐标公式即得M坐标，CD⊥AB，得kCD，同理得点N坐标，直线MN恒过定点归结为用参数把直线的方程表示出来，无论参数如何变化这个方程必有一组常数解．

【解题分析】(Ⅰ)由题意知F(1,0)，

所以抛物线的标准方程为y2=4x.

(3分)

(Ⅱ)证明:由题意知直线AB的斜率存在且不为0，

设lAB：y=k(x-1)(k≠0)，代入y2=4x，

得k2x2-2(k2+2)x+k2=0，

(7分)

同理，可得N(2k2+1，-2k)．

所以直线MN的方程为

(9分)

化简整理，得(k2-1)y=k(3-x)，

故不论k为何值，直线MN恒过点(3,0)．

(12分)

20.【细磨题】(本小题满分12分)

已知A(1,2)为抛物线y2=2px(p>0)上的一点，E,F为抛物线上异于点A的两点，且直线AE的斜率与直线AF的斜率互为相反数.

(Ⅰ)求直线EF的斜率；

【命题意图】本题考查直线与抛物线的位置关系，考查运算求解能力、数形结合思想，考查数学运算、数据分析、直观想象、逻辑推理的核心素养.

【解题分析】解法一：(Ⅰ)设E(x1,y1),F(x2,y2)，

因为点A(1,2)为抛物线y2=2px(p>0)上的一点,所以y2=4x.

(1分)

设直线AE:y=kx+(2-k),

因为直线AE的斜率与直线AF的斜率互为相反数,

所以直线AF:y=-kx+(2+k),

k2x2+[2k(2-k)-4]x+(2-k)2=0，

(2分)

(3分)

(4分)

所以直线EF的斜率kEF=-1.

(5分)

直线l:x=ty+m,代入y2=4x,

得y2-4ty-4m=0,

所以y3+y4=4t,y3y4=-4m.N(-m,0),

(6分)

(8分)

(10分)

作过点P,Q垂直于x轴的直线,分别交x轴于点B,D,

(12分)

解法二：(Ⅰ)设E(x1,y1),F(x2,y2).

因为点A(1,2)为抛物线y2=2px(p>0)上的一点，所以y2=4x，

(1分)

(3分)

因为直线AE的斜率与直线AF的斜率互为相反数,

(4分)

(Ⅱ)设直线l的方程为l:x=ty+m.

P(x3,y3),Q(x4,y4),N(-m,0),

代入y2=4x,得y2-4ty-4m=0,

所以y3+y4=4t,y3y4=-4m.

(6分)

(7分)

由题可知

=(x3+m-λ(x4+m),y3-λy4)

(12分)