基于管状导体模型钢轨内阻抗计算

(兰州交通大学自动化与电气工程学院，甘肃兰州，730070)

钢轨作为牵引回流和轨道电路信号电流的通道，其阻抗直接影响着轨道电路的传输性能[1]。当钢轨中有交流电流时，由于集肤效应的存在，电流主要集中分布在钢轨表面，导致钢轨横截面电流密度分布不均匀，从而致使钢轨电阻增加和内电感降低。钢轨内阻抗是钢轨阻抗计算中的重要参数，准确计算钢轨内阻抗对于牵引供电系统中钢轨阻抗建模具有重要意义。目前，国内外学者对钢轨内阻抗的计算进行了大量研究。DWIGHT等[2]研究了无限宽平面导体和管状圆柱形导体的集肤效应，为研究钢轨内阻抗提供了理论依据。吴命利等[3]采用含Bessel 函数的内阻抗公式直接计算了管状导体和实心圆柱形导体的内阻抗，但未曾考虑大参数下内阻抗计算问题。ARNOLD 等[4-6]提出不同条件下各种内阻抗计算的近似公式，并研究了正方形截面、矩形截面、空心圆截面等不同横截面导体的内阻抗，避免了直接计算Bessel 函数，但计算结果误差较大。DOMMEL等[7-8]通过对Bessel函数进行多项式近似和渐近展开计算了圆导线的内阻抗。BROWN 等[9]将钢轨等效为圆柱形导体，利用修正Bessel函数计算了较低频率下(60 Hz以下)钢轨内阻抗，计算结果精度较高，但仅适用于低频情况，高频时直接计算修正Bessel函数将出现数值计算不稳定、难以收敛的问题。彭涛等[10]将钢轨等效为管状导体，通过简化Bessel函数表示的内阻抗公式，近似计算了高频时钢轨内阻抗；HILL 等[11]基于电磁场有限元法研究了钢轨内阻抗随电流、频率的变化规律，发现有限元结果与实测数据误差较小，表明有限元法可用于钢轨内阻抗的计算，计算精度高，但所需计算资源较大。AMOS 等[12-13]通过编程计算了Bessel 函数及其修正形式，但在大参数下计算时，由于出现数值计算不稳定而无法应用到导体单位内阻抗求解中。朱峰等[14]利用钢轨横截面面积相等的原则，计算了等效半径，将钢轨等效为实心圆导体，推导出内阻抗的计算公式，并利用余弦函数和多项式近似计算Bessel函数，得到大参数下内阻抗计算公式，但计算结果与仿真结果及实验数据相比误差较大；VUJEVIĆ 等[15]对修正Bessel 函数进行缩放，得到了实心和管状圆柱形导体的内阻抗，计算精度高且避免了数值计算问题，但对于钢轨这种不规则截面导体未提及。本文作者根据钢轨横截面面积及周长，计算得到钢轨等效半径，将钢轨等效为管状导体模型，在此基础上，利用修正Bessel函数表示出管状导体的内阻抗计算公式。针对大参数下计算修正Bessel函数时出现的数值计算不稳定及收敛困难问题，利用缩放比例因子，对修正Bessel函数进行缩放，并采用数值积分法对缩放后的修正Bessel函数求解，计算得到钢轨内阻抗公式。最后，利用该公式分析钢轨电阻与内电感随电流频率、幅值的变化规律。同时，基于有限元法对P60型钢轨模型进行仿真计算，将仿真结果与计算结果进行对比，验证计算结果的准确性，以期为牵引供电系统建模时钢轨内阻抗的计算提供参考。

1 钢轨内阻抗计算公式

1.1 钢轨等效模型

钢轨横截面与圆导线不同，呈现为“工”字形的不规则形状，考虑集肤效应时无法直接计算其内阻抗，需将钢轨等效为管状圆柱形导体。当钢轨中存在直流电流时，将不会出现集肤效应，电流均匀分布在钢轨横截面，故根据钢轨横截面面积相等的原则计算得到等效半径ra；当钢轨中存在交流电流时，由于集肤效应的存在，钢轨横截面中电流分布不均匀，主要集中分布在钢轨表面，故根据钢轨横截面周长相等的原则计算得到等效半径，即管状导体外半径re。按照钢轨横截面与等效管状导体横截面相等原则，计算管状导体半径：

式中：s为钢轨横截面积；l为钢轨截面周长；ri和re分别为等效管状导体的内、外半径。

钢轨等效管状圆柱形导体的内、外半径示意图如图1所示。

图1 钢轨等效管状导体Fig.1 Rail equivalent tubular conductor

选取钢轨长度为1 m，电导率σ=6×106S m，计算不同型号钢轨的基本参数，如表1所示。

表1 不同型号钢轨的基本参数Table 1 Basic parameters of different types of rails

1.2 直流内阻抗计算公式

导体的直流内阻抗包括导体本身的直流电阻与直流电感，直流电阻由导体的物理性质决定，仅与导体的电导率、横截面积有关。根据表1中数据，将钢轨等效为管状导体模型，则单位长度管状导体的直流电阻Rdc为

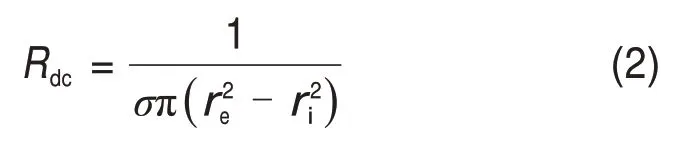
式中：σ为导体电导率。

在电磁学中，当圆柱形导体流过直流电流时，导线的内部和外部都有磁场存在，将产生内磁通和外磁通，由此产生的电感有内电感和外电感，外电感与导体尺寸及所处环境有关，内电感与电流频率有关。本文仅研究导体的内电感，根据内磁通、电流及内电感的关系，计算直流电流下单位长度圆柱形导体内电感。首先，根据文献[16]定义导体内电感Ldc为

式中：ψ为圆柱形导体内部总磁链；I为通过圆柱形导体横截面的总电流。

而对于圆柱形导体，根据安培环路定律及磁感应强度计算其内部总磁链ψ[17]：

式中：μ=μrμ0，为导体磁导率；μr为导体相对磁导率；μ0=4π×10-7H/m，为真空磁导率。

根据式(3)和式(4)，得到直流电流下单位长度圆柱形导体内电感为

1.3 交流内阻抗计算公式

考虑集肤效应而忽略邻近效应计算圆导线的内阻抗时，涉及Bessel 函数及其修正形式[3]。由于钢轨横截面不规则，因此，将钢轨等效为管状圆柱形导体，其内阻抗计算公式可以用Bessel 函数、修正Bessel函数表示，而修正Bessel函数所表示的内阻抗公式与Bessel 函数所表示的内阻抗公式相比，其数值计算稳定性更好且计算精度较高。对于管状圆柱形导体，内阻抗为导体表面电场强度与流过导体横截面总电流之比，利用修正Bessel函数，导体内阻抗-Z可表示为

式中：ω=2πf，为角频率(f为频率)；j 为虚数单位；α为衰减常数。

文献[18]中给出了集肤电阻比与集肤内电感比的定义，利用式(2)～(6)，计算管状圆柱形导体的集肤电阻比与内电感比：

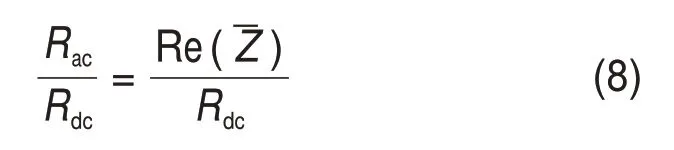
式中：Rac为交流电流下单位长度导体电阻；Re()表示内阻抗的实部；Lac为交流电流下单位长度导体内电感；Im()表示内阻抗的虚部。

以P60 型钢轨为例，根据式(8)和式(9)计算集肤电阻比与内电感比随参数αr(r为管状导体内外半径之差)的变化，其中，参数αr作为修正Bessel 函数中的变量，其取值直接影响内阻抗公式数值计算的稳定性，而钢轨的高磁导率、高频率、高电导率及大物理尺寸都会使αr变大，因此，引入该参数描述大参数情况，集肤电阻比与内电感比计算结果分别如图2(a)和图2(b)所示。

从图2可以看出：当参数αr超过48 后，计算结果出现震荡，导致数值计算不稳定，计算结果不可靠，甚至无法得出计算结果。

其原因如下：1)在第1 类和第2 类修正Bessel函数所表示的内阻抗公式中，由于第2类Bessel函数值的数量级比第1类Bessel函数值小e2·--γ·r，而内阻抗公式中包含分数及各种运算，导致计算时数值计算不稳定；2)大参数会导致利用软件直接计算Bessel函数时出现收敛困难，使计算结果超出计算机的技术限制。由参数αr可知，高频率、高磁导率以及大物理尺寸等因素都将导致出现大参数问题，而对于钢轨这种铁磁材料，电导率、磁导率均较大。同时，钢轨作为信号电流和牵引电流回流的共同通道，信号电流频率范围为1 700～2 600 Hz，牵引电流频率为工频50 Hz，钢轨中电流频率分布范围宽。以上原因将导致计算钢轨内阻抗时出现大参数问题。

基于原因1)所导致的计算内阻抗时出现的数值计算不稳定问题，利用缩放比例因子对第1类和第2类修正Bessel函数进行缩放，缩放关系为：

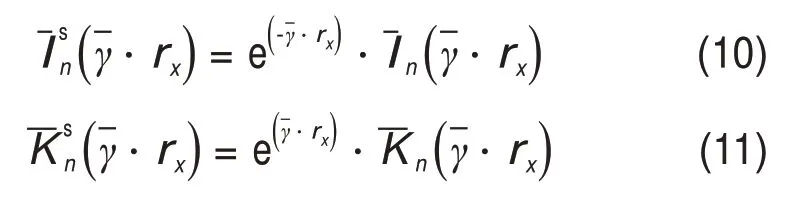
式中：n=0,1，表示Bessel函数的阶数；x为i和e，分别表示管状导体的内半径与外半径。

由式(10)和式(11)可知：第1类修正Bessel函数缩小了，而第2 类修正Bessel 函数放大了，使第1 类和第2 类修正Bessel 函数数值的数量级接近，因此，计算内阻抗时避免了数值计算不稳定问题。根据式(6)、式(10)及式(11)，缩放后内阻抗计算公式为

从图3可以看出：缩放内阻抗计算公式后，集肤电阻比与内电感比在计算时稳定，消除了数值计算不稳定问题。

图2 集肤电阻比和内电感比与参数αr的关系Fig.2 Relationship between skin resistance ratio and internal inductance ratio with parameter αr

图3 缩放后集肤电阻比和内电感比与参数αr的关系Fig.3 Relationship between skin resistance ratio and internal inductance ratio with parameter αr after scaling

2 计算修正Bessel函数

计算修正Bessel函数时，一般采用无穷级数和的方法，但当大参数出现时，将使级数项增多，出现级数收敛困难，无法直接使用软件计算。因此，采用数值积分法计算修正Bessel函数。

2.1 第1类修正Bessel函数计算

第1类零阶修正Bessel函数，采用数值积分法可将其表示为

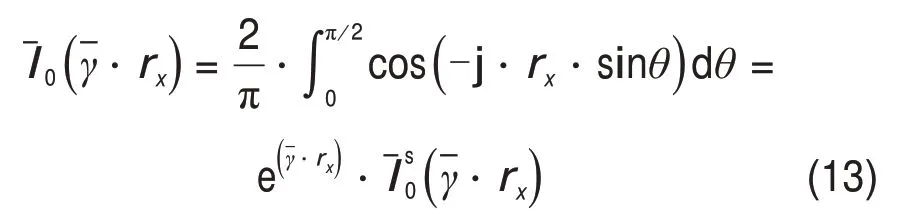
式中：θ为积分变量，取值为[0，π/2]。

根据缩放关系及欧拉公式简化式(13)并分离等式的实部与虚部，则缩放后第1类零阶修正Bessel函数可表示为

式中：a和b为关于大参数及积分变量的中间变量，其表达式为

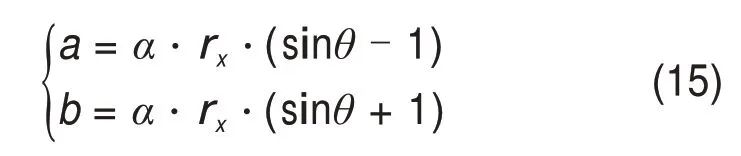
第1类一阶修正Bessel函数，采用数值积分法可将其表示为

根据缩放关系及欧拉公式简化式(16)并分离等式的实部与虚部，则缩放后第1类一阶修正Bessel函数可表示为

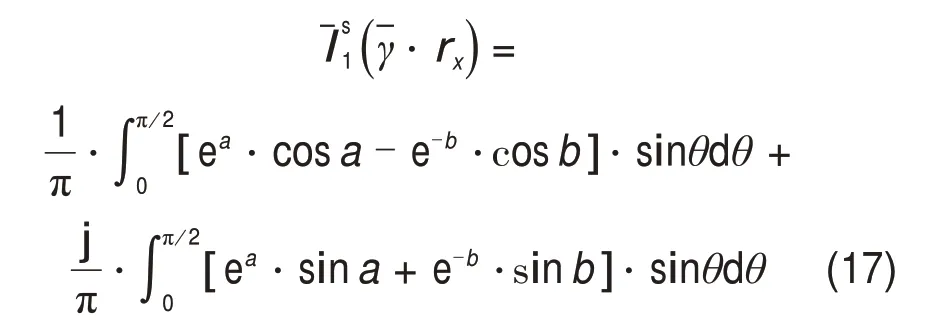
2.2 第2类修正Bessel函数计算

第2类零阶修正Bessel函数，采用数值积分法可将其表示为

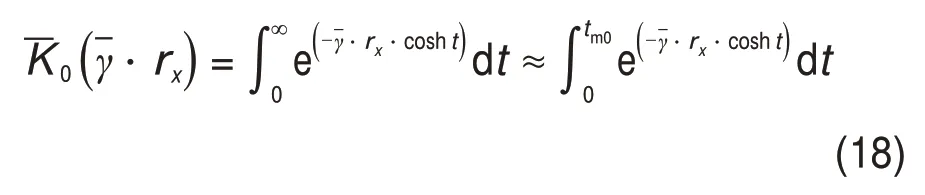
式中：t为积分变量，取值为[0，tm0]；tm0为将无穷积分区间截断后转换为有限积分区间的上限，

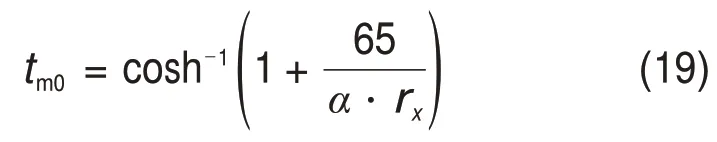
根据缩放关系及式(18)，采用截断法求取积分上限，并分离等式的实部与虚部，则缩放后第2类零阶修正Bessel函数可表示为

式中：d为关于大参数及积分变量的中间变量，其表达式为

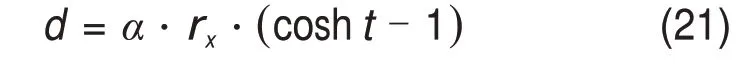
第2类一阶修正Bessel函数，采用数值积分法可将其表示为

式中：tm1为将无穷积分区间截断后转换为有限积分区间的上限。

基于式(13)～(23)，采用数值积分法分别计算出第1 类零阶、一阶修正Bessel 函数及第2 类零阶、一阶修正Bessel函数，避免了以往采用无穷级数和法求解大参数下修正Bessel函数时出现收敛困难的问题。

3 有限元仿真

以60 kg/m 的P60 型钢轨为例，按照钢轨的实际形状绘制钢轨模型，并根据实际情况设置钢轨材料参数。在仿真中钢轨电导率σ=6×106S/m，相对磁导率假定为μr=100，且钢轨周围为空气。考虑到交流电流流经钢轨时出现集肤效应(集肤效应实际为涡流效应)，使用涡流求解器进行求解，将激励设为正弦工频电流。仿真中对钢轨进行网格剖分时，由于钢轨横截面呈“工”字型，形状不规则，而对有限元中二维区域剖分时，通常采用三角形单元和矩形单元，矩形单元适合离散矩形区域，三角形单元可用于离散不规则区域，因此，选择三角形单元划分钢轨二维模型。考虑集肤效应的影响，仿真时电流频率范围为0～104Hz，当频率达到104Hz时，钢轨最小集肤深度为0.2 mm，因此，钢轨表面网格划分时单元边长小于0.2 mm。网格划分结果如图4所示，钢轨表面由于集肤效应的存在，网格剖分更密。最后，进行仿真计算，得到钢轨横截面的电流密度分布图，如图5所示。由图5可见，电流主要集中分布在钢轨表面。

通过计算涡流场中的电场损耗(欧姆损耗)和磁场储能(平均能量)，分别得到钢轨电阻和内电感。根据表1中P60型钢轨基本参数及仿真中所设置的材料参数，利用数值积分法即式(13)～(22)，编程计算修正Bessel函数，并利用缩放后内阻抗计算公式得到钢轨等效为管状导体后的电阻及内电感，将计算结果与有限元仿真结果比较，二者相对误差δ为

图4 钢轨有限元网格划分Fig.4 Finite element meshing of rail

图5 钢轨电流密度分布Fig.5 Current density distribution of rail

式中：y为计算结果；y0为有限元仿真结果。

根据式(12)计算得到单位长度钢轨电阻、内电感与频率的变化关系，计算结果分别如图6～8所示。

从图6可以看出：P60 型钢轨电阻随电流频率的增大而增大，在频率较低时，电阻变化趋势显著，随着频率的增大，电阻变化趋势逐渐变缓。

从图7可以看出：P60 型钢轨电感随电流频率的增大而减小，且计算结果与仿真结果相比较，误差较大。其主要原因是钢轨处于无限开域中，而在仿真计算时，采用一定大小的求解域代替无限开域，且钢轨周围被空气所包围，因此，仿真计算的电感包括模型的外电感与内电感，外电感与钢轨周围环境有关，而采用内阻抗计算公式计算电感时，仅计算了钢轨内电感。由于集肤效应，随着电流频率增加，钢轨内部电流趋向于钢轨表面分布，根据文献[19]可知，当电流频率达到1 MHz时，电流基本集中分布在钢轨表面，此时可认为钢轨内部无电流分布，即单位长度钢轨内电感为0 μH/m，从而得到钢轨外电感，将有限元计算得到的电感数据减去外电感即为钢轨内电感。钢轨内电感随频率变化的关系如图8所示，由图8可见，钢轨内电感变化趋势与钢轨电感随频率变化趋势相一致。根据式(24)得到钢轨电阻和内电感的计算结果与仿真结果之间的相对误差，如图9所示。

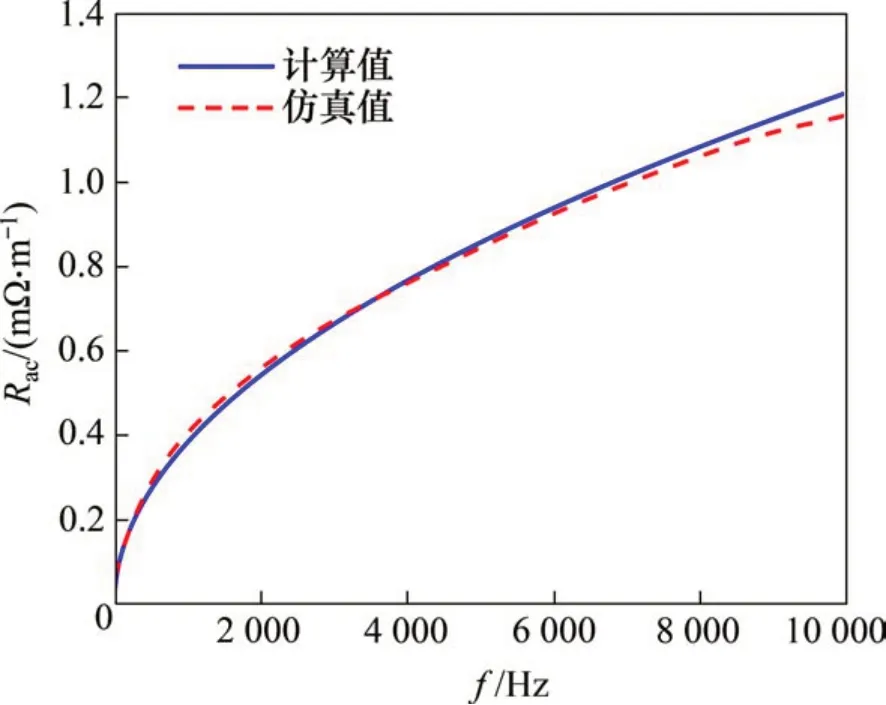
图6 P60钢轨电阻与频率的关系Fig.6 Relationship between P60 rail resistance and frequency

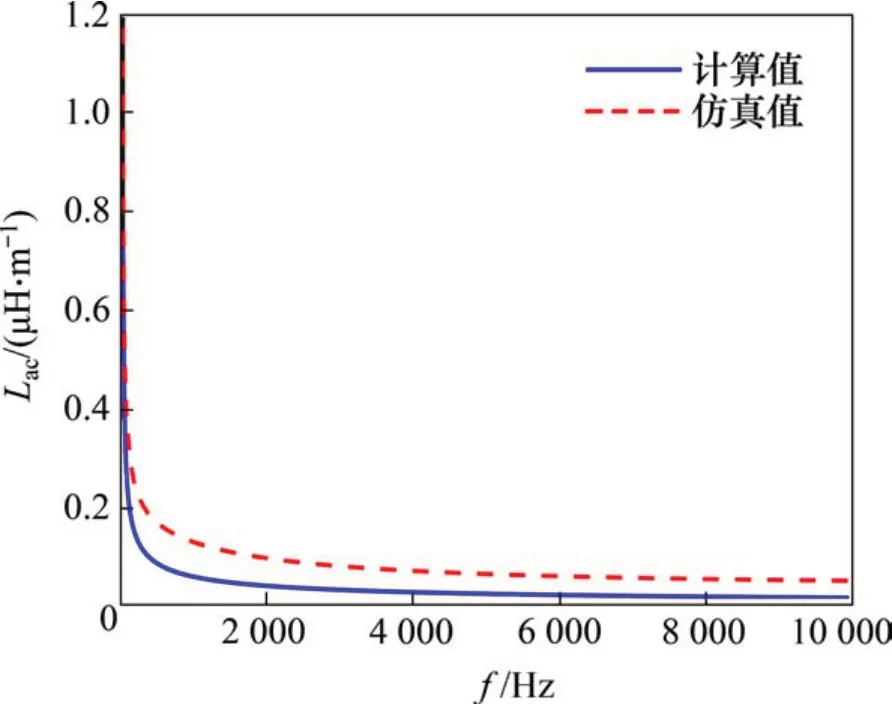
图7 P60钢轨电感与频率的关系Fig.7 Relationship between P60 rail inductance and frequency

图8 P60钢轨内电感与频率的关系Fig.8 Relationship between P60 rail internal inductance and frequency

图9 频率变化时钢轨电阻和内电感计算结果与仿真结果的相对误差Fig.9 Relative error between the calculated results and the simulated results of rail resistance and internal inductance with frequency variation

从图9可以看出：当频率在0～104Hz 范围内时，钢轨电阻相对误差小于4%，而钢轨内电感相对误差小于5%，因此，计算结果与有限元仿真结果之间相对误差均在±5%以内。

4 钢轨内阻抗影响分析

4.1 电流频率影响

电气化铁路系统中，轨道电路信号电流频率较高，而牵引回流频率为工频50 Hz，频率较低。钢轨为牵引回流与信号电流的共同通道，因此，流经钢轨的电流频率范围较宽。为研究不同型号钢轨电阻、内电感随电流频率的变化规律，设定研究频率范围为0～10 kHz。根据表1中不同型号钢轨的基本参数，采用数值积分法编程计算缩放后第1 和第2 类修正Bessel 函数，将其代入缩放后内阻抗计算式(12)，计算结果分别如图10和图11所示。由图10～11可见，单位长度钢轨电阻、内电感与电流频率呈非线性关系。

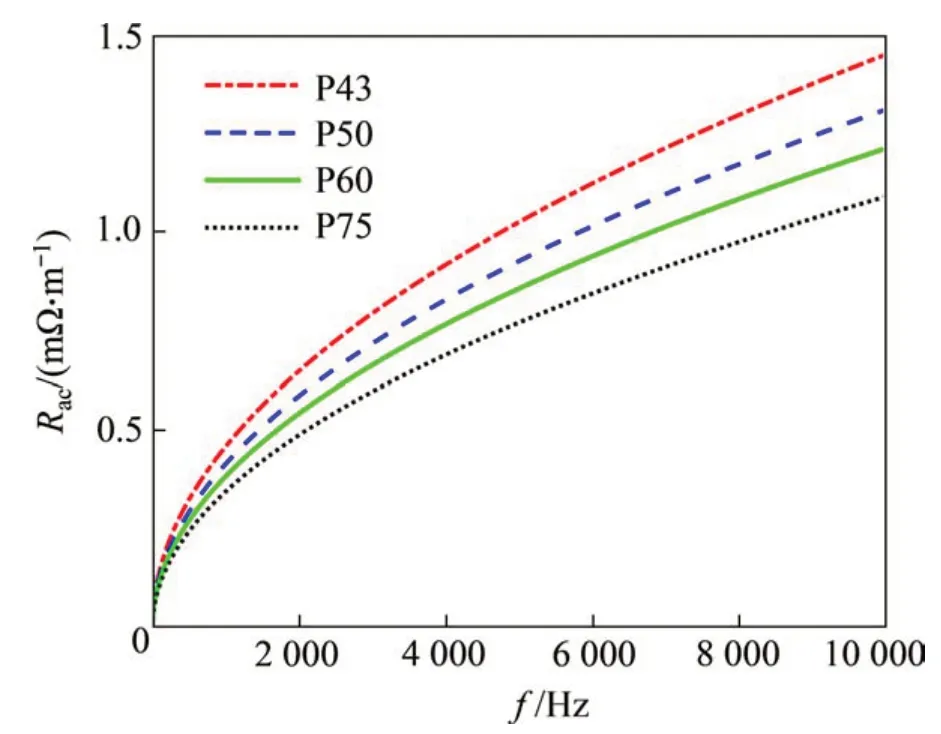
图10 不同型号钢轨电阻与频率的关系Fig.10 Relationship between rail resistance and frequency of different types of rails

图11 不同型号钢轨内电感与频率的关系Fig.11 Relationship between rail internal inductance and frequency of different types of rails

从图10可以看出：钢轨电阻随电流频率的增加而增大；在频率较低时，电阻增大趋势比较明显，而随着频率逐渐增加，电阻增大趋势变缓。针对不同型号钢轨可以看出，在同一频率下，钢轨横截面越小，钢轨电阻越大。

从图11可以看出：钢轨内电感随电流频率的增加而减小。在频率较低时，内电感减小趋势比较明显；随着频率的增加，内电感变化越来越小，逐渐趋于零；在同一频率下，钢轨横截面越小，内电感越大，但差值较小，因此，钢轨型号对钢轨内电感影响较小。

4.2 电流幅值的影响

钢轨是铁磁性材料，不同电流幅值会导致钢轨相对磁导率发生变化，且出现磁饱和现象，因此，不同电流幅值下钢轨内阻抗也将发生变化。而对于电气化铁路系统，钢轨中存在轨道电路信号电流与牵引电流回流，信号电流较小，幅值一般为毫安级，而牵引电流回流幅值较大，一般为几百安培。因此，研究电流幅值对钢轨内阻抗影响时，主要考虑工频50 Hz 牵引电流回流的影响。对于牵引供电系统，当列车在不同工况下运行时，钢轨中牵引电流回流大小不一，如长编组的高速动车组满负荷运行时，流经钢轨的电流可高达800 A；而当高速动车组在站内停靠时，流经钢轨的电流幅值小于30 A。为研究电流幅值对钢轨内阻抗的影响，以P60型钢轨为例，设定电流幅值范围为100～1 000 A，频率为50 Hz。通过安培环路定理，计算不同电流幅值所产生磁场的磁场强度，根据文献[20]中P60型钢轨的μr-H曲线(μr为相对磁导率，H为磁场强度)，得到与电流幅值对应的钢轨相对磁导率，结果如表2所示。

表2 工频情况下不同电流幅值对应的钢轨相对磁导率Table 2 Relative permeability of rail corresponding to different current amplitudes at power frequency

在工频情况下，将表2中相对磁导率数据代入式(12)，计算得到钢轨电阻与内电感随电流幅值变化的规律，分别如图12～13 所示。根据式(24)计算电流幅值变化时钢轨电阻与内电感计算结果与仿真结果之间的相对误差，结果如图14所示。

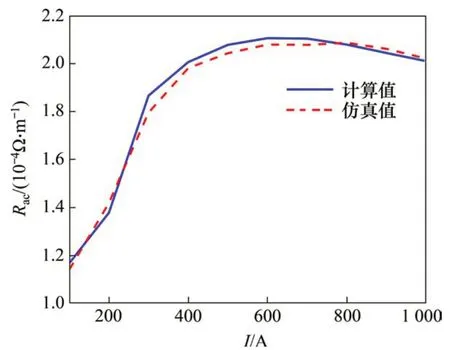
图12 P60钢轨电阻与电流幅值关系Fig.12 Relationship between P60 rail resistance and current amplitude

图13 P60钢轨内电感与电流幅值关系Fig.13 Relationship between P60 rail internal inductance and current amplitude

从图12和图13可以看出：钢轨电阻、内电感与电流幅值呈非线性关系，且钢轨电阻与内电感随电流幅值变化趋势一致，均随电流幅值的增大而增大；当增大到最大值后，开始缓慢减小。这主要是由于钢轨是铁磁材料，存在磁饱和效应，即当电流幅值增大时，钢轨相对磁导率增大，但当电流幅值超过某一定值(如表2中电流超过600 A)时，相对磁导率开始减小，从而导致钢轨电阻与内电感随电流幅值的增大呈现出先增大而后缓慢减小的现象。从图14可以看出：当电流幅值在100～1 000 A 变化时，钢轨电阻和内电感计算结果与仿真结果之间的相对误差均在±5%以内。

图14 电流变化时钢轨电阻和内电感计算结果与仿真结果的相对误差Fig.14 Relative error between calculated results and simulated results of rail resistance and internal inductance with current variation

5 结论

1)基于钢轨等效管状导体模型，采用缩放比例因子缩放内阻抗计算公式，通过数值积分法进行计算，避免了大参数下数值计算不稳定及收敛困难问题，将钢轨电阻和内电感的计算结果与仿真结果对比，发现二者的相对误差在±5%以内。

2)利用缩放修正Bessel 函数表示的内阻抗公式，计算得到的钢轨电阻与内电感随电流频率的变化曲线，表明该公式正确地反映了钢轨电阻随频率增大而增大且内电感随频率增大而减小的变化规律。

3)不同型号钢轨在同一频率下，钢轨电阻差异较大，且钢轨横截面积越小，电阻越大；不同型号钢轨内电感差异较小，钢轨横截面积对内电感影响较小。

4)绘制了钢轨电阻与内电感随电流幅值变化的曲线，由于钢轨是铁磁材料，钢轨电阻与内电感随电流幅值的增大呈现先增大而后缓慢减小的变化趋势。

5)提出了准确计算钢轨内阻抗的公式，可为牵引网建模时钢轨内阻抗计算提供参考。