刀刃结构对镍合金切削过程影响的数值模拟
(华南理工大学机械与汽车工程学院,广东广州,510640)
迅猛发展的航空航天技术对材料的性能提出了越来越高的要求,镍合金Inconel 718 因其优异的抗疲劳性能、高温强度和稳定性等性能,在航空航天等领域得到了广泛应用[1-2]。Inconel 718 是最难切削的材料之一,其特殊的物理和化学性质能导致切削刃的磨损。在金属切削中,刀刃与工件直接接触,刀刃轮廓和锋利度等刀刃特征影响着刀具寿命和已加工表面质量。对于锋利刀具,其刀刃常容易出现毛刺和崩刃等缺陷,导致刀具寿命缩短、已加工表面质量下降,因此,在切削前常需将刀刃进行修整和钝化[3]。通过刃口钝化制备的具有微结构的刀刃,其机械强度提升,承受载荷改变,减少了初始裂纹的形成[4]。事实上,钝圆刀刃已被证实能够提高刀具寿命以及成品质量[5]。然而,为了分析钝化刀刃对切削过程的影响,以及为了能够制备特定、合适的刀刃以适用于指定的载荷分布,进一步研究钝圆刀刃结构对切削过程的影响是有必要的。刀刃经过刃口钝化可以转变为倒角刀刃和钝圆刀刃。钝圆刀刃可分为对称和不对称2 种类型,对于不对称钝圆刀刃,仅用钝圆半径rβ来描述刀刃结构并不合适且存在误差。由DENKENA等[6]提出的K系数法更适用于描述钝圆刀刃的微几何结构,K系数法包含4个描述刀刃几何结构的基本参数Sγ,Sα,-S和K,其中Sγ和Sα分别为刀刃与前刀面和后刀面的2个过渡点到理想刀尖的距离,-S(即(Sγ+Sα)/2)为刀具的平均钝圆半径,K(即Sγ/Sα)为形态系数。对于刀刃自身和刀刃对切削过程的影响,学者们进行了相关研究。WYEN等[4]提出了一种描述刀刃结构的新方法,使得钝圆刀刃的尺寸能够被唯一确定,同时还分析了使用不同钝圆半径的刀具切削得到的切削力和摩擦因数。BASSETT 等[7]提出了一种制备高质量刀刃的方法,且使用多种不同结构的钝圆刀具系统地探究了刀刃结构对切削力、刀具磨损、涂层刀具寿命的影响。加工过程引起的微观结构变化是表征已加工表面质量的指标之一。切削过程中发生的加工硬化和动态再结晶是一种普遍现象,影响着工件的微观结构。在已加工表面附近,当变形工件的局部总位错超过临界值时,相应区域将发生动态再结晶并导致晶粒度的改变,影响成品的性能和质量[8]。此外,经由刀尖流向已加工表面的材料体积也影响着已加工表面质量即影响成品的最终尺寸,而这一体积与刀刃结构息息相关。目前,关于刀刃结构对微观结构变化影响的研究尚不多[9];另一方面,由于数值模拟分析具有能减少为优化加工工艺而进行的实验次数等优点,当前模拟分析与具体实验的结合已成为研究镍合金切削过程的重要手段,因此,利用有限元模拟研究刀刃结构对镍合金已加工表面质量的影响,对于理解材料微观结构的演变和指导实际刀具的选用以控制已加工表面质量具有一定意义。JAFARIAN 等[9]通过有限元模拟探究了钝圆刀具和倒角刀具对Inconel 718 微观结构变化的影响,结果表明,增大钝圆刀具的钝圆半径和倒角刀具的倾斜角度能细化材料已加工表面晶粒并提高表面硬度,且刀刃类型对切削影响层深度的影响程度比刀具几何参数的大。SHEN等[10]使用多种切削刃模拟Inconel 718 的切削过程并考虑热载荷影响和耕犁作用,研究了刀刃微结构对工件已加工表面残余应力的影响。刀刃结构影响着刀具寿命和性能、刀具所承受的热力载荷和材料已加工表面质量,应用有限元模拟研究刀刃结构对切削过程的影响,对于指导刀具的制备和选用具有重要意义,也有利于加深对材料微观结构变化的认识。因此,本文作者利用DEFORM-2D 有限元软件,针对刀刃结构对Inconel 718 切削过程的影响展开数值模拟分析,比较不同刀具下的模拟切削力和摩擦因数、材料流动情况,并进行材料晶粒度和硬度的有限元模拟试验。
1 有限元模型建立
1.1 正交切削模型的建立及验证
本文使用DEFORM-2D 有限元软件进行平面正交切削模拟,所建立的有限元模型如图1所示。在此模型中,刀具由于硬度远大于材料硬度而设为刚体,其网格数设为2 500个;工件设为刚塑性体,其网格数设为7 000个。利用网格密度窗口在切削区域附近设置高度密集的网格以获得更精确的模拟结果,其中最小的网格边长约为3 μm;此外,DEFORM 通过网格自适应重划分技术保证模拟的正常进行。刀具的EF和FG边界在竖直方向和水平方向的速度均设为0;工件的BC边界在竖直方向固定,而沿水平方向的速度设为切削速度,其余边界不设定速度边界条件。在热传导方面,模型中工件的ABC边界和刀具的DEF边界设定为室温20 ℃,工件的ADC边界和刀具的GDE边界设定为热交换边界;刀-屑间接触良好,且为了快速达到热稳定状态,刀-屑间热传递系数设为100 kN/(s·mm·℃)。刀-屑接触面的摩擦机理十分复杂,在本模拟中,刀-屑接触面的摩擦简化为常剪切摩擦,即

式中:τ为摩擦剪应力;m为剪切摩擦因数;k为工件流动剪应力。

图1 正交切削有限元模型Fig.1 Finite element model of orthogonal cutting
模拟试验的工件材料为Inconel 718,其弹性模量为214.6 GPa,泊松比为0.305,热传递系数为17.8 W/(10-3K),比热容为3.62 J/(kg·K),热膨胀系数为14.8 μm/(10-3K)。刀具材料为硬质合金,其热导率33.5 W/(10-3K),比热容为234 J/(kg·K),密度为12 700 kg/m3。切削过程伴随着大应变、高温、高应变率,本模拟将使用DEFORM预设的Johnson-Cook模型。
由于切削力的测量难度较小,所以,切削力常用于验证模拟结果的可靠性。引用SHI[11]的Inconel 718切削实验数据,如表1所示,实验所用刀具前角γ=0°,后角α=5°,钝圆半径rβ=20 μm。根据文献[11],在DEFORM-2D 中设定相同的切削条件,并使用前述建立的有限元模型进行切削模拟。只要摩擦因数经过合适校正,切削力就可以得到较好预测,而不依赖于摩擦模型的类型[12]。经试验,当剪切摩擦因数设为m=0.5时,模拟切削力与实验切削力较吻合(如图2所示),说明在此摩擦因数下所建立的模型具有一定的可靠性。
本文试验刀具的刀刃结构通过DENKENA等[6]提出的K系数法表示,所有刀具的前角均为-6°,后角均为6°,而Sγ=12~100 μm,Sα=12~100 μm,钝圆刀具几何结构如图3所示。待切厚度(进给量)f=0.01,0.02,0.04,0.05,0.06,0.10,0.15 和0.20 mm,所有试验的切削速度v均为30 m/min,在此速度下,Inconel 718不会形成锯齿状切屑[13]。
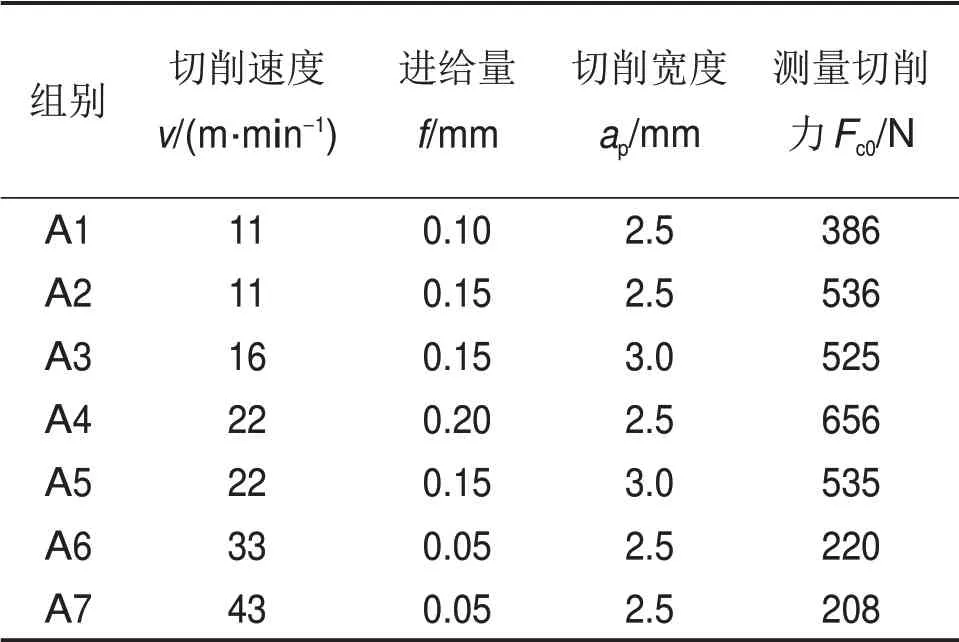
表1 Inconel 718正交切削实验数据[11]Table 1 Orthogonal cutting experiment data of Inconel 718[11]
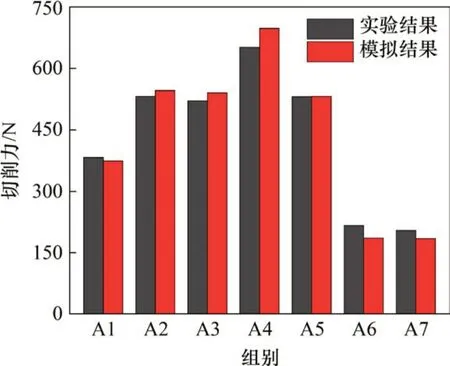
图2 模拟切削力和实验切削力比较Fig.2 Comparison of modeling and experimental cutting forces
1.2 晶粒度和硬度的有限元模拟
材料晶粒细化和硬度改变的模拟通过DEFORM 用户自定义子程序实现。应用Zener-Hollomon 关系式预测由动态再结晶导致的晶粒度改变,这一关系式结合了温度和应变率2个重要参数;应用Hall-Petch公式预测已加工表面和次表面的硬度变化。Zener-Hollomon 参数Z的表达式如下:

式中:为应变率;R=8.314 5 J/(K·mol),为理想气体常数;Q为激活能;T为热力学温度。再结晶晶粒度d的计算与Zener-Hollomon参数相关联,即

式中:d0为初始晶粒度;a和m为材料常数,通常用b来表示d0与a的积。b可由关于进给量f的等式表示[14]:

硬度H的改变与再结晶后的晶粒度d紧密联系,由Hall-Petch公式表示:

式中:C0和C1为材料常数。根据JAFARIAN等[14]的研究,式(2)~(5)中Q=386 kJ/mol,C0=378,C1=298.4。此外,再结晶晶粒度计算式中的m=0.010,在本模拟中修改为m=0.012。
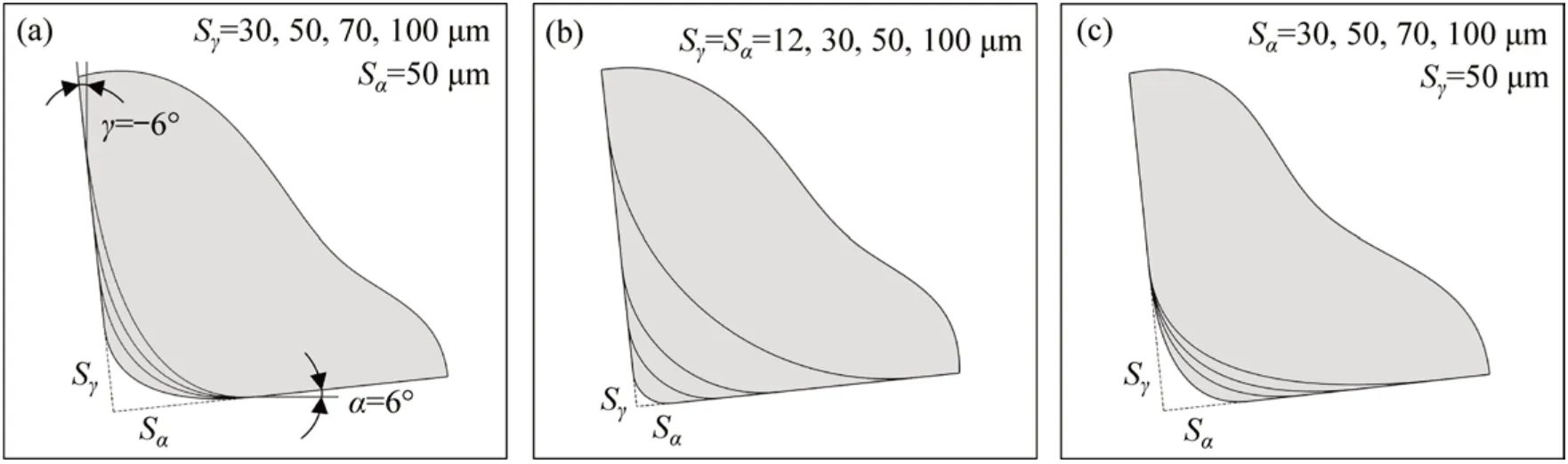
图3 钝圆刀具的几何结构Fig.3 Honed cutting tools geometries
临界应变的确定对于晶粒度的预测十分关键,这一参数决定了触发材料微观结构改变的起始值,即应变必须达到临界应变才能触发动态再结晶的发生。临界应变εcr的计算式为[14]

式中:为应变率。
通过DEFORM 的用户自定义子程序进行Inconel 718微观结构演变的模拟,其具体步骤如图4所示。图4中,dt和Ht分别为每一模拟步完成后的晶粒度和硬度。在模拟的每一步中,针对网格的每一单元都要计算Zener-Hollomon参数(简称为Z-H 参数)和临界应变。单元应变只有在超过临界应变时才会触发动态再结晶,此时,由式(3)计算的晶粒度将会取代前一步的晶粒度,同时,该单元的硬度随之发生相应的变化;否则,单元的晶粒度和硬度将维持前一步的数值。单元的初始晶粒度和维氏硬度分别设为18 μm和429[14]。

图4 模拟微观结构变化的流程图Fig.4 Flow chart of modeling microstructure evolution
2 模拟结果与分析
2.1 钝圆刀具结构对切削力与摩擦因数的影响
随着Sγ和Sα的增大,刀刃的锋利程度下降,切削力分散,导致材料的切除需要更大的切削力。图5所示为当切削速度v=30 m/min时,使用3种类型的钝圆刀具在进给量f=0.01,0.02,0.04,0.05,0.06,0.10,0.15 和0.20 mm 下切削Inconel 718 得到的主切削力Fc和进给力Ff,如图5所示。从图5可看出:在f≥0.02 mm时,主切削力和进给力都随进给量的增大而呈线性增大。比较钝圆刀具结构对主切削力的影响(见图5(a),(c)和(e))可知:Sα和Sγ对主切削力的影响并不明显,而随平均钝圆半径增大,主切削力的变化才相对明显。比较钝圆刀具结构对进给力的影响(见图5(b))可知:当Sγ单独变化时,进给力的变化并不明显。从图5(d)和(f)可知:当和Sα增大时,进给力都明显增大,由此可知这两者对进给力的影响都比Sγ的大,其中对进给力的影响程度最大。
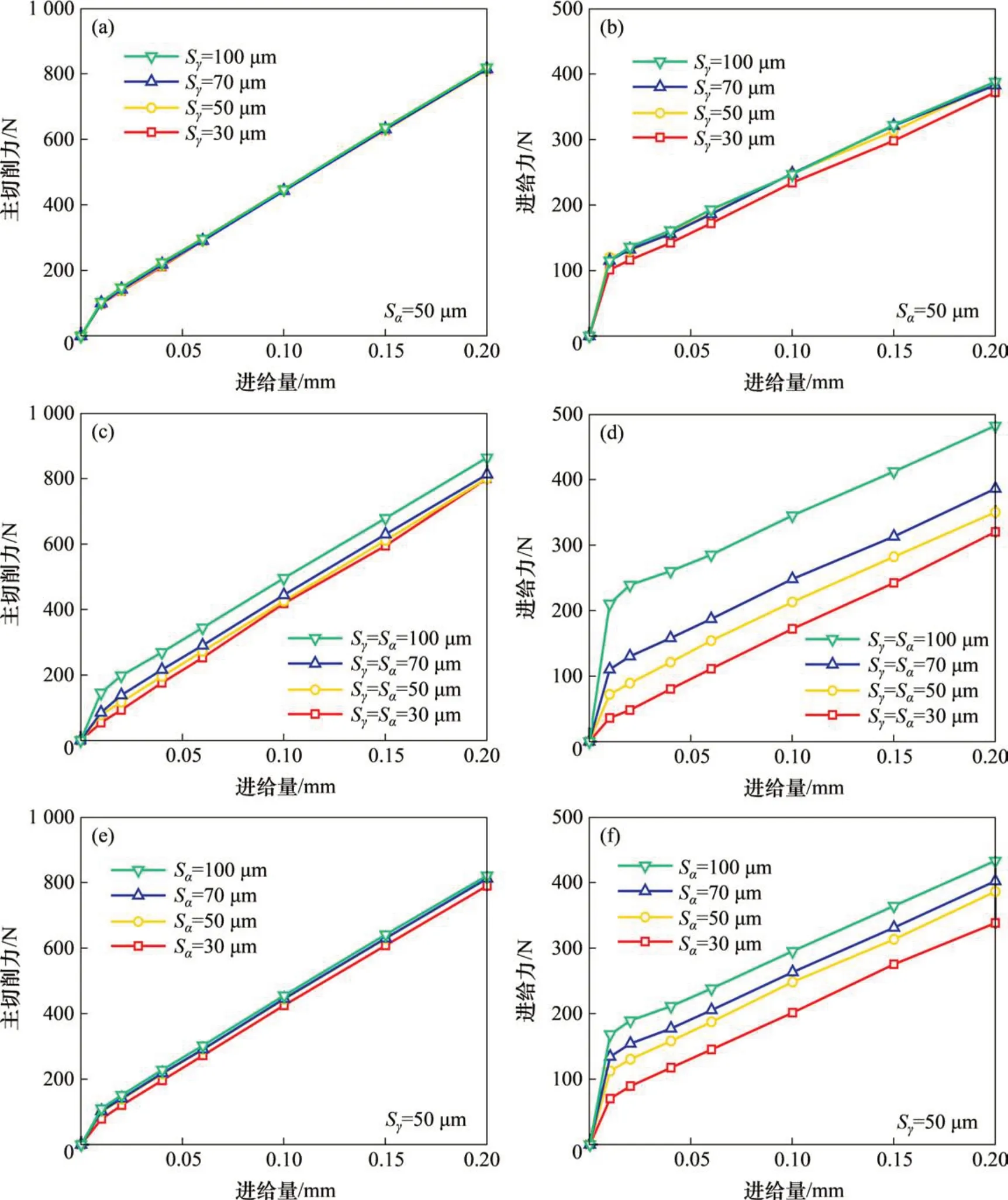
图5 3种钝圆刀具下的主切削力Fc和进给力FfFig.5 Cutting forces Fc and feed forces Ff under 3 types of honed tools
当待切厚度(进给量)小于某个临界值时,钝圆的尺寸效应对切削力的影响将变得明显。图6所示为3种类型的钝圆刀具在不同进给量下的主切削力和进给力变化情况,据此可以研究进给量和刀刃结构对切削力比值μ(μ=Ff/Fc)的影响。从图6(a),(b)和(c)可以观察到,存在某个进给量的临界值使主切削力和进给力相等,超过此临界点时,μ=Ff/Fc<1;低于此临界点时,μ=Ff/Fc>1;而增大Sγ,Sα或-S都将使临界点向右偏移。同时,由图6可判断,临界点的位置与刀刃结构有关,在图6(a)中,增大Sγ临界点的位置变化很小;在图6(b)和(c)中,增大和Sα时临界点位置发生较大程度的变化,表明Sα对进给量临界点位置变化的影响比Sγ的更大。
图5和图6所示结果充分说明了刀刃钝圆对切削力的影响。为深入理解刀刃钝圆对切削力的影响,ALBRECHT[15]提出了一种模型,将切削力分解为作用在钝圆区域的耕犁力Fpl和作用在前刀面上的切屑力FQ,如图7所示,其中,Fa为合力,Qt和Qn分别为切屑力FQ平行和垂直于前刀面的分力,μQ为前刀面上的摩擦因数。提出这一模型的前提假设是:当刀具角度不变时,切屑力FQ的方向保持不变,而FQ的取值与待切厚度h呈线性关系;前刀面上切削力的比值保持不变,即摩擦因数μQ保持不变[15]。通过确定图5中10种不同尺寸刀具的切屑力FQ和摩擦因数μQ对Albrecht 的假说进行验证,即若μQ不受刀具钝圆的影响,则其数值将保持不变。
为了确定摩擦因数,需要先行确定耕犁力分量。耕犁力分量可以通过线性外推法获得,由已知切削力线性外推得到待切厚度h=0 mm时的切削力即为耕犁力分量,这一方法首先由THOMSEN等[16]提出,下面通过钝圆刀具的切削力变化曲线进行解释。图8所示为钝圆刀具Sγ=Sα=100 μm时,切削力随进给量(即待切厚度h)的变化。从图8可以观察到,当h增大至0.03~0.04 mm时,主切削力Fc和进给力Ff随h呈线性增长,与此同时钝圆对切削力的影响开始消失。对于未磨损从而不受钝圆影响的理想刀刃,当h=0 mm 时其切削力将为0 N。如图8所示,对主切削力和进给力呈线性增长的部分利用线性外推法所获得的直线,其截距分别为耕犁力Fpl在切削方向和进给方向的分量Fpl,c和Fpl,f,通过此方法即可确定刀具的耕犁力分量。
切屑力FQ、耕犁力Fpl和摩擦因数μQ可由式(7)~(10)确定:

式中:FQ,c和FQ,f分别为切屑力FQ沿水平方向和竖直方向的分力。
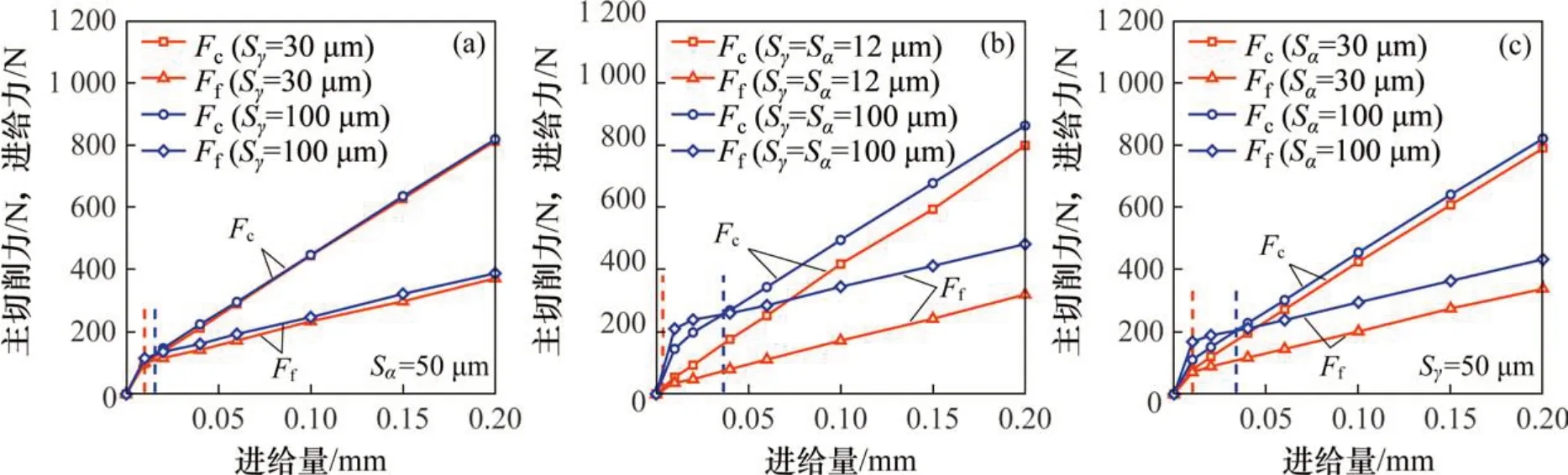
图6 3种钝圆刀具下主切削力Fc及进给力Ff变化趋势的比较Fig.6 Comparison of trends of cutting force Fc and feed force Ff under 3 types of honed tools
由线性外推法及式(7)~(10)确定图5中10 种尺寸刀具的切屑力和摩擦因数,当待切厚度h=0.10 mm 时的切屑力和摩擦因数如图9所示。由图9可知:随着平均钝圆半径的增大,切屑力的变化很小,其平均值FQ,mean=406 N,表明Sγ和Sα对切削力的这一分量都没有明显影响,因此,钝圆产生的影响可以仅通过平均钝圆半径-S描述;此外,摩擦因数μQ随平均钝圆半径的增大几乎保持为一常数,其平均值为μQ,mean=0.51,这一结果验证了ALBRECHT[15]的假说,即μQ不受刀具钝圆的影响,同时也与BASSETT等[7]所得结论相同。
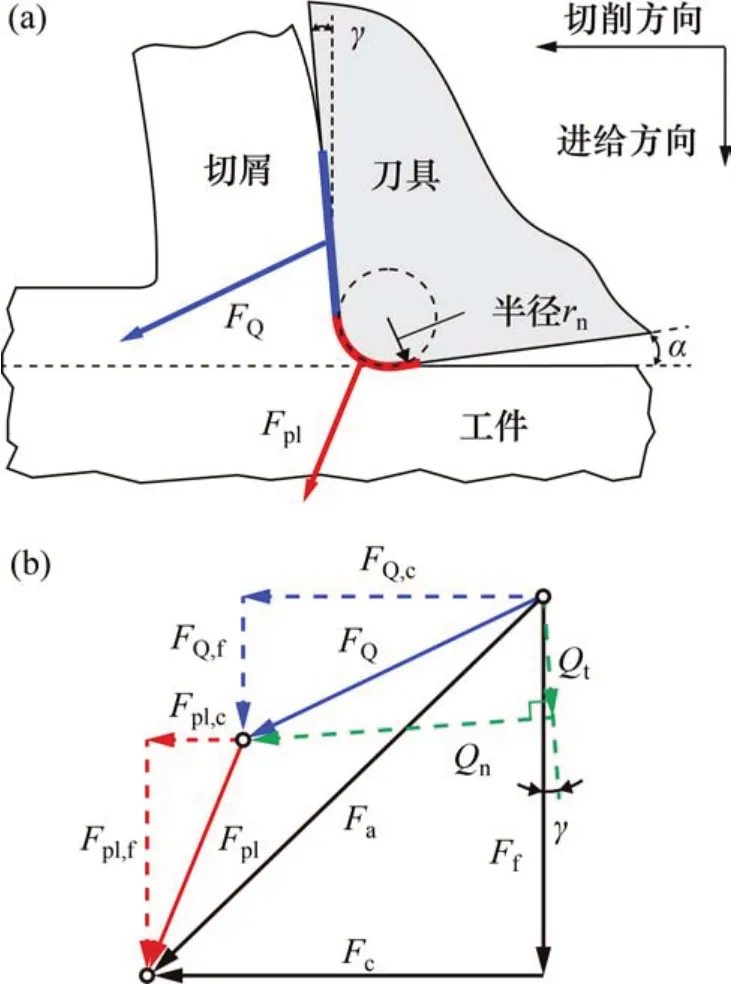
图7 耕犁力Fpl和切屑力FQ及其分量示意图[15]Fig.7 Schematic of ploughing force Fpl and chip force FQ and their components[15]

图8 钝圆刀具Sγ=Sα=100 μm时的切削力Fig.8 Process forces under the honed tool with Sγ=Sα=100 μm

图9 不同刀具下的切屑力FQ和摩擦因数μQFig.9 Chip forces FQ and friction coefficients μQ under different cutting tools
2.2 材料流动
早期已有实验证明,使用倒角刀具切削时,在倒角下方将形成材料滞留区,在材料滞留区停留的材料将充当刀具的有效刀刃进行切削[17-18]。而当使用钝圆刀具切削时,在变形区中同样会出现材料滞留区,只是范围较小。在切削速度v=30 m/min、进给量f=0.15 mm 的条件下,使用不同尺寸钝圆刀具切削Inconel 718 的材料速度分布模拟结果如图10所示。由图10可知:对于对称钝圆刀具(K=Sγ/Sα=1),材料滞留区随钝圆半径的增大而增大;对于不对称钝圆刀具(K<1 和K>1),材料滞留区也随着Sγ和Sα的增大而增大,但比较图10(b)和(f)的变化以及图10(c)和(e)的变化时,可以发现Sγ对材料滞留区范围的影响比Sα对材料滞留区范围的影响大。从图10可知:对称刀具形成的材料滞留区比不对称刀具的更大,其尺寸变化时对滞留区范围的影响也更大。此外,从图10还可以发现,当刀具平均钝圆半径相同时,K>1时形成的材料滞留区范围大于K<1时形成的材料滞留区范围。
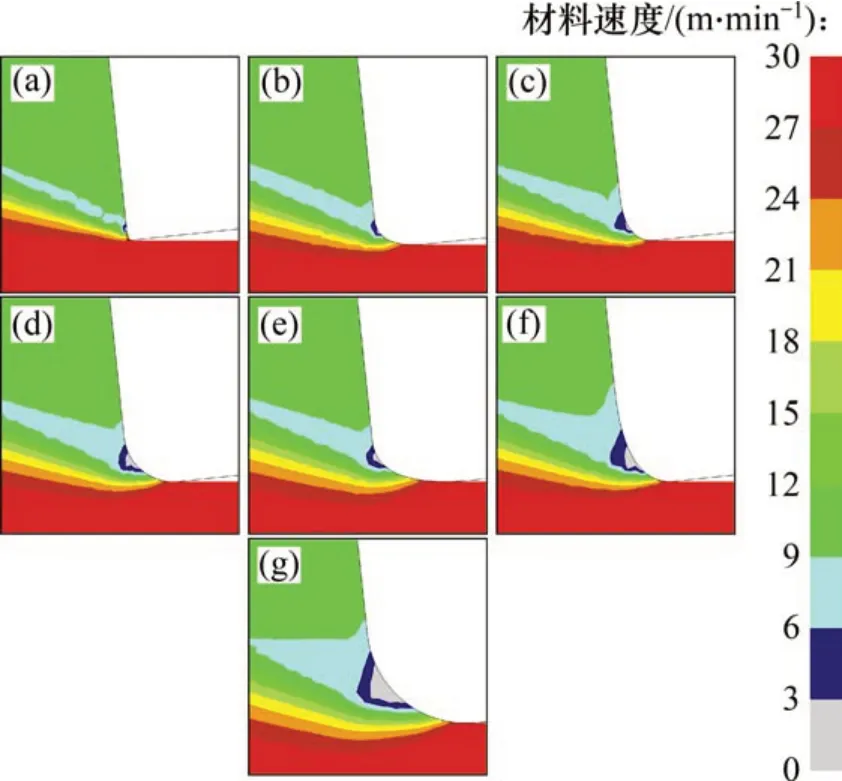
图10 不同钝圆刀具下的材料速度分布Fig.10 Distribution of material velocity under different honed tools
图11所示为使用理想刀具和钝圆刀具切削Inconel 718得到的流线网格、速度矢量和等效应变分布情况。从速度矢量分布图中可以观察到材料分离点的存在,材料分离点与刀刃的形状密切相关,在这一点附近材料的速度很小并沿前刀面和后刀面2个方向发生分离。从速度矢量的模拟结果可以直观看出,材料分离点的位置hmin随着Sγ和Sα的增大而上移。由图11(c)和(d)可知:当Sα>Sγ时,材料分离点的位置hmin更高,说明Sα对材料分离点的影响更大。与图11(c)和(d)相比,图11(b)中的hmin则比前两者的都大,说明对称刀具对材料分离点的影响比不对称刀具的更大。材料分离点的位置确定了材料流向前刀面和后刀面的体积,影响着已加工表面质量,即影响成品的最终尺寸。对于理想切削刃,材料分离点的位置几乎与刀尖持平,则刀具切除的有效材料厚度与名义待切厚度基本相等;而使用钝圆刀具进行切削时,材料分离点随着钝圆尺寸的增大而上升,材料流向后刀面的体积随之增大。
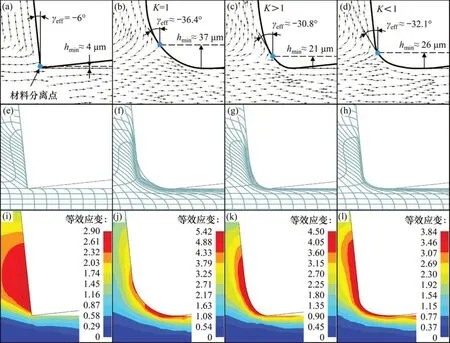
图11 理想刀具和钝圆刀具对材料流动的影响Fig.11 Influences of ideal and honed tools on material flow
通过分析图11中的流线网格及其对应的等效应变分布进一步了解材料的流动情况,流线密集处表明材料发生了剧烈的塑性变形,已加工表面处流线的密集程度反映了材料流向后刀面的体积。由图11的流线网格分布可见:与钝圆刀具相比,理想刀具的前刀面和后刀面的流线都比较稀疏而均匀,与刀尖持平的1条流线在由待加工状态向已加工状态转变的过程中几乎没有变化,加工前后此流线可以保持在同一水平线上。由图11所示的等效应变分布可见:理想刀具的等效应变分布相对来说较为疏散,表现为前刀面附近不同等效应变梯度的分布范围很大,而在后刀面的等效应变分布范围较小,最大等效应变2.90 出现在前刀面附近。
刀具下与刀尖持平的流线在材料分离前后的变化情况在一定程度上反映材料分离点的高度,使用钝圆刀具切削时这条流线在扭曲后其末端偏向前刀面,扭曲程度越大,表明其末端与已加工表面的距离越大。图11(g),(h),(f)中的流线扭曲程度依次增大,相应地,图11(c),(d),(b)中的材料分离点的位置也依次提高。刀刃结构对材料分离点的影响由材料流向后刀面的体积间接说明。在图11(h)中已加工表面处的流线稍比图11(g)中的密集,而前刀面处的流线比图11(g)中的稀疏,证明图11(h)中材料流向后刀面的体积更大,而图11(g)中材料流向前刀面的体积更大,也间接说明了Sα对材料分离点的影响更大。分析图11(k)和图11(l)的等效应变分布可知,最大等效应变分别为4.50 和3.84,且都出现在前刀面至钝圆一带,图11(k)在钝圆靠上一带出现了十分集中的应变且数值较大,而钝圆靠下一带至已加工表面的应变相对来说则较小;图11(l)中前刀面至钝圆一带的应变集中程度比图11(k)中的小,出现的最大等效应也比图11(k)中的小,但在已加工表面处高等效应变的梯度在水平方向延伸得较远,图11(g)和(k)以及图11(h)和(l)中的流线分布与等效应变分布情况大体吻合。图11(f)中,无论是前刀面还是后刀面流线都更加密集,尤其是接近后刀面处(与图11(g)和(h)相比),证明了材料流向后刀面的体积更大,间接说明对称刀具对材料分离点的影响比不对称刀具的更大;图11(j)中的等效应变在钝圆靠下一带进一步集中,最大等效应变高达5.42,说明钝圆与材料之间的挤压和摩擦十分剧烈,高等效应变的梯度沿已加工表面延伸得较远,与流线分布情况比较吻合。
2.3 倒角刀具和钝圆刀具晶粒度和硬度的模拟

图12 Sγ=Sα=100 μm倒角刀具和钝圆刀具下的晶粒度和维氏硬度预测Fig.12 Predictions of grain size and Vickers hardness under chamfered and honed tools with Sγ=Sα=100 μm
在切削速度v=30 m/min、进给量f=0.10 mm的条件下,比较Sγ=Sα=100 μm的倒角刀具和钝圆刀具(刀具角度相同)下Inconel 718已加工表面的模拟晶粒度和硬度,结果如图12所示。由图12可知:模拟的已加工表面稳定状态区域的晶粒度和硬度分布较均匀,而刀尖附近的温度尚未稳定,因此,对微观结构变化的研究应关注切削稳态区域。模拟结果表明,正交切削Inconel 718 时,已加工表面和次表面的微观结构确实发生了剧烈变化,同时可以发现已加工表面发生的晶粒细化导致相应区域的硬度强化。图12(a)和(c)中倒角刀具下已加工表面受影响层的深度沿稳态区域方向扩大的趋势较明显,而图12(b)和(d)中使用钝圆刀具切削获得的晶粒度和维氏硬度分布沿深度方向则较均匀。
根据图12(a)所示的稳态区域获取晶粒度和维氏硬度沿已加工表面深度的分布情况,结果如图13所示。由图13可知:钝圆刀具下已加工表面的表层(表面深度为0 mm)晶粒度(5.28 μm)小于倒角刀具下的表层晶粒度(5.69 μm);相应地,钝圆刀具下已加工表面的表层维氏硬度(508)稍高于倒角刀具下的表层维氏硬度(505)。尽管使用钝圆刀具切削时获得了更小的晶粒,但在倒角刀具切削下已加工表面的受影响层更深,钝圆刀具切削影响的深度约为0.20 mm,而倒角刀具的影响深度约为0.25 mm。

图13 已加工表面的模拟晶粒度和维氏硬度Fig.13 Modeling grain size and Vickers hardness in machined surface
Inconel 718 微观结构的模拟结果说明,应用DEFORM 用户自定义子程序能够实现晶粒度和硬度的预测,由相同Sγ和Sα及刀具角度的倒角刀具和钝圆刀具模拟得到的晶粒度和硬度具有一定的辨识度,但仍需通过具体的实验确定相关模型和公式参数并比较实验结果和模拟结果,以确认其可靠性。
3 结论
1)主切削力受平均钝圆半径-S以及刀刃与前刀面和后刀面的2个过渡点到理想刀尖的距离Sγ与Sα的影响均较小,而进给力随-S和Sα增大时明显增大。存在与刀刃结构有关的进给量临界点,使切削力比值μ=Ff/Fc=1;进给量小于此临界点时μ>1,而进给量大于此临界点时,μ<1。Sα对临界点位置的影响比Sγ的影响大。
2)当切削力分解为耕犁力Fpl和切屑力FQ时,刀刃钝圆Sγ和Sα的变化对切屑力FQ和前刀面上的摩擦因数μQ的影响很小,μQ几乎保持为一常数。
3)材料滞留区随Sγ和Sα的增大而增大,Sγ对材料滞留区范围的影响比Sα的影响大;材料分离点随Sγ和Sα的增大而上升,Sγ对材料分离点的影响比Sα的影响小。对称刀具对材料流动的影响比不对称刀具的大。
4)应用用户自定义子程序能够实现微观结构的模拟,由相同Sγ和Sα及刀具角度的倒角刀具和钝圆刀具模拟得到的晶粒度和硬度具有一定的辨识度。

