一种基于Volterra频域核的非线性频谱智能表征方法

(西安交通大学机械制造系统工程国家重点实验室，陕西西安，710049)

类似于线性系统的传递函数，Volterra 核将线性系统卷积扩展成一系列多维卷积形式，能够描述非线性系统的本质特性，具有物理意义明确、信息量丰富等优点，引起了国内外学者的广泛关注[1-4]。相对于Volterra时域核，Volterra频域核只与系统自身特性有关，不会随输入变化而变化，人们可以直观、准确地观察到许多非线性现象，因而更受关注[5]，而且Volterra 频域核也被广泛应用于机械系统和电子控制系统的非线性分析[6-7]。目前，有关Volterra 频域核的应用和研究得到了快速发展，特别是以基于广义频率响应函数(GFRF)和基于非线性输出频率响应函数(NOFRF)为代表的非线性频谱研究逐渐被应用于特征提取、机理分析和故障诊断领域[8-12]；而非线性频谱计算方法复杂度和准确度是制约其应用的关键。目前有关非线性频谱计算方法有递推法[13-14]、批量最小二乘法[15-16]和自适应计算方法[17-19]。其中，递推法是依据非线性系统微分方程，将微分方程中相关参量代入递推公式来计算GFRF/NOFRF 幅值，因此，递推法计算非线性频谱的准确性完全依赖于数学模型的正确性。批量最小二乘法是一种非参数计算方法，不依靠系统数学模型，无需了解系统内部机理，仅依靠系统的输入和输出，通过矩阵求逆运算即可估计出各阶频谱幅值；自适应计算方法可克服最小二乘法求逆计算量大的缺陷，根据实际输出与估计输出偏差值动态调整算法中参数，从而计算各阶频谱幅值。但是，该方法是对频点进行逐一计算，无法满足基于数据驱动的非线性频谱分析需求。针对上述非线性频谱计算方法存在的问题，迫切需要一种新的频谱智能计算方法，实现系统非线性频谱的快速、准确表征。BP 神经网络是一个并行分布式信息处理网络，网络中的神经元具有强大的逼近和拟合能力，可以逼近任意非线性函数。梁丽等[20-21]利用BP 神经网络实现了Volterra时域核的计算；吴世浩等[22]利用BP神经网网络对Volterra 频域核进行计算，取得了较好的效果。为此，本文作者结合非线性频谱特点，设计一种BP 神经网络，对2 种常见的GFRF 和NOFRF 幅值进行智能计算，并通过仿真实验验证该方法的有效性。

1 基于Volterra 频域核的非线性频谱理论值计算

连续时不变非线性动态系统的输入和输出关系可以用Volterra级数表示，即

式中：t为时间；τ为维度变量；y(t)为系统输出；u(t)为系统输入；hn(τ1,τ2,…,τn)为第n阶Volterra时域核或广义脉冲响应函数。对其进行多维傅里叶变换可得到

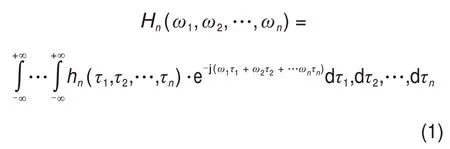
Hn(ω1,ω2,…,ωn)称为第n阶Volterra 频域核或广义频率响应函数(GFRF)。

鉴于GFRF计算量比较大，ZHU等[23]在此基础上提出了非线性输出频率响应函数(NOFRF)，即

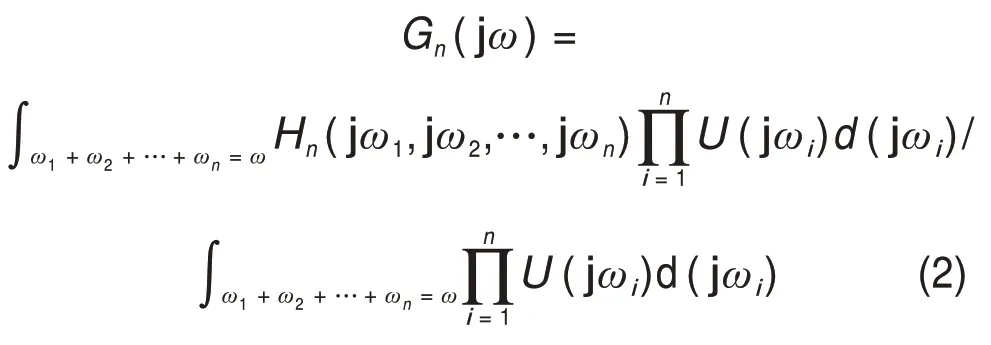
GFRF 幅值的精确计算可采用递推方法[14]，而NOFRF 幅值的计算采用批量最小二乘法准确度比较高，下面对该方法进行分析。

用输入信号Aiu*(t)激励系统M次，其中，i=1,2,…,M，M≥N；Ai为常数，且AM>AM-1>…>A1> 0；u*(t)为随时间变化信号，经过傅里叶变换之后为U*(jω)，系统得到M次输出频谱记为Yi(jω)(i=1,2,…,M)，则

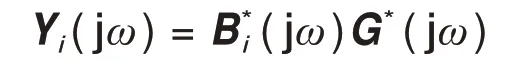
式中：Yi(jω)=[Y1(jω),…,YM(jω)]T；B*i(jω)=的傅里叶变换；G*(jω)=[G*1(jω),…,G*N(jω)]T为NOFRF各阶幅值，

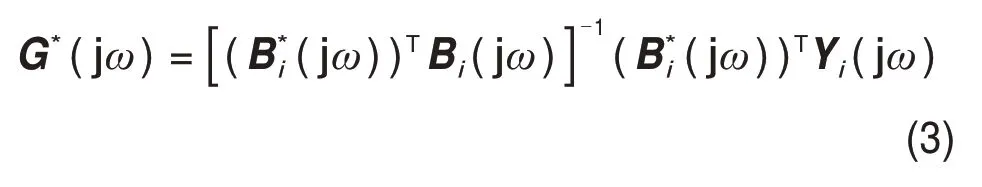
2 基于BP 网络的非线性频谱幅值智能计算

采用BP神经网络对GFRF或NOFRF等非线性频谱幅值进行计算是以系统真实频谱幅值为依据，利用BP网络强大的拟合能力，通过对网络训练实现测试值与真实值逼近。因此，非线性频谱幅值的真实值是否准确直接影响智能计算精度的高低。一般而言，GFRF 和NOFRF 的真实值分别按照递推算法[14]和批量最小二乘算法[19]对式(1)和(3)进行准确计算。而在实际中，对一个系统非线性频谱的计算往往转化为黑箱问题进行辨识操作，由于辨识模型比较复杂，依靠辨识方法求解非线性频谱存在计算量大和计算准确率低等问题。

BP 神经网络是典型的多层前向网络，能够逼近任意非线性函数，因此，可以利用该特性实现非线性频谱的智能计算，1 个简单的3 层神经网络模型如图1所示。

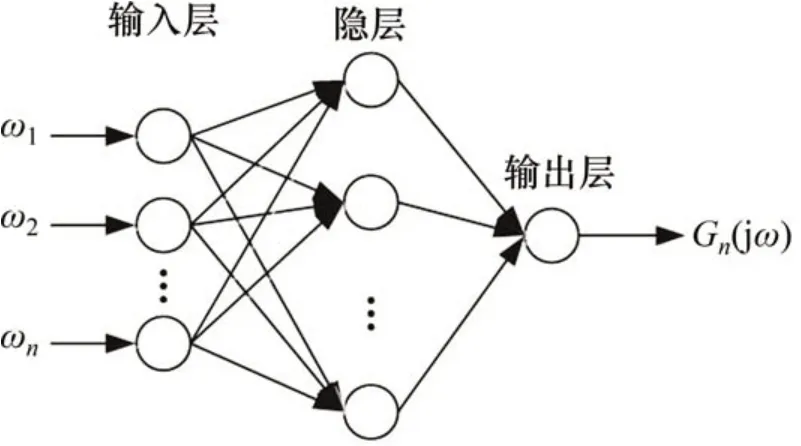
图1 基于BP网络的非线性频谱计算Fig.1 Nonlinear spectrum computation based on BP network

从式(1)可以看出，一阶GFRF包含1个频率变量，二阶GFRF包含2个频率变量，n阶GFRF频包含n个频率变量，因此，对于不同阶次的GFRF可以利用BP 网络进行分阶进行计算。与GFRF 不同的是，NOFRF是一维的，各阶NOFRF仅包含1个频率变量，因此，BP的输入量为1。

对于BP 神经网络，激活函数和隐层神经元数量选择直接影响输出结果。常用的激活函数有正切S 型函数、对数S 型函数、ReLU 函数和线性函数，由于机器人驱动系统的GFRF 和NOFRF 真实幅值范围皆为(0，1)，因此，本文选择可导且连续的sigmoid激活函数，即

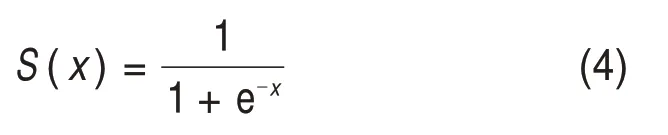
隐层神经元数量对BP 网络的性能影响很大，若神经元数量过小，则计算精度较低；若神经元数量过大，则会出现过拟合现象。基于此结合非线性频谱的特性，本文将均方根误差(ERMSE)作为评价指标确定合理的隐层神经元数量，即

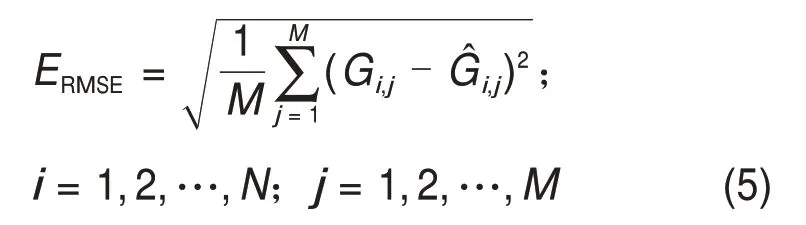
式中：Gi,j为第i阶第j个频率点对应的GFRF 或NOFRF幅值的预测值；为第i阶第j个频率点对应的GFRF 或NOFRF 幅值的真实值。ERMSE表示预测值和真实值之间差异样本标准偏差，反映了样本离散程度，在非线性拟合时，ERMSE越小，其逼近效果就越好。

在数据归一化方面，为了消除较大频率范围对数据的影响，同时，针对本文选取的激活函数类型，本文采用标准归一化方法，将数据归一化到[0，1]，即

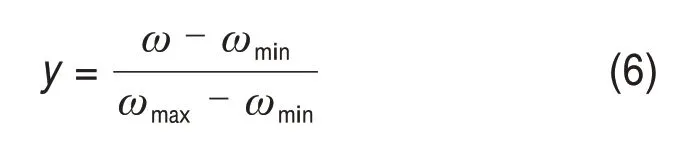
式中：ωmin为频率最小值；ωmax为频率最大值。

以前2阶GFRF和前4阶NOFRF为例，采用基于BP神经网络的非线性频谱进行智能计算，流程如图2所示。具体计算流程如下：

1)建立非线性系统的数学模型，确定输入和输出变量；

2)根据建立的数学模型，利用递推公式，求出前2阶GFRF幅值真实值；

3)选择适当的激励信号进行多次激励，并采集输出数据，利用式(3)的批量最小二乘算法求出前4阶NOFRF幅值真实值；

4)针对GFRF 模型，设计2 种BP 神经网络(二阶GFRF 的计算模型中输入是频率的二维组合)，通过对网络进行训练，获得前2 阶GFRF 幅值估计值；

5)针对NOFRF 模型，设计1 种BP 神经网络(网络的输入是一维频率数据)，通过对网络训练，估计出前4阶NOFRF幅值。

3 仿真实验

本文以工业机器人用永磁同步电机为研究对象对其故障进行诊断，永磁同步电机的数学模型[24]可以表示为

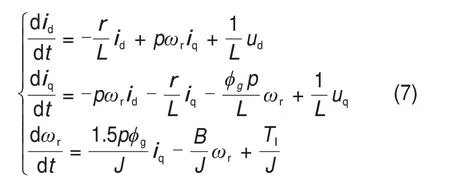
式中：id和iq分别为定子绕组d和q轴电枢电流；ud和uq分别为定子绕组d和q轴定子指定电压，为了便于分析，本文假设ud=0；L为定子绕组电感；φg为永磁体产生的磁链；r为定子绕组电阻；J为转子转动惯量；Tl为负载转矩；B为转子阻尼系数；p为极对数；ωr为转子角速度。对式(7)进行分析，选取id为系统输入，ωr为系统输出，可得到非线性微分方程为

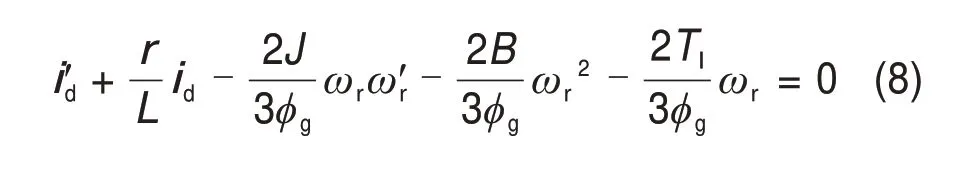
式中：i′d和ω′r分别为id和ωr的导数。

3.1 GFRF的智能计算

对于已知的数学模型，利用递推公式可求得前2阶GFRF幅值理论值，即

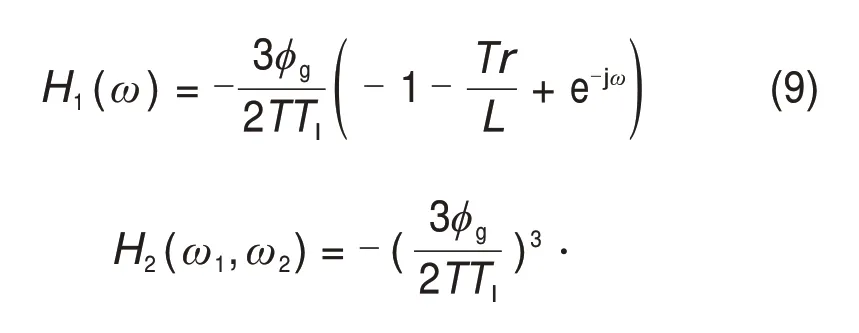
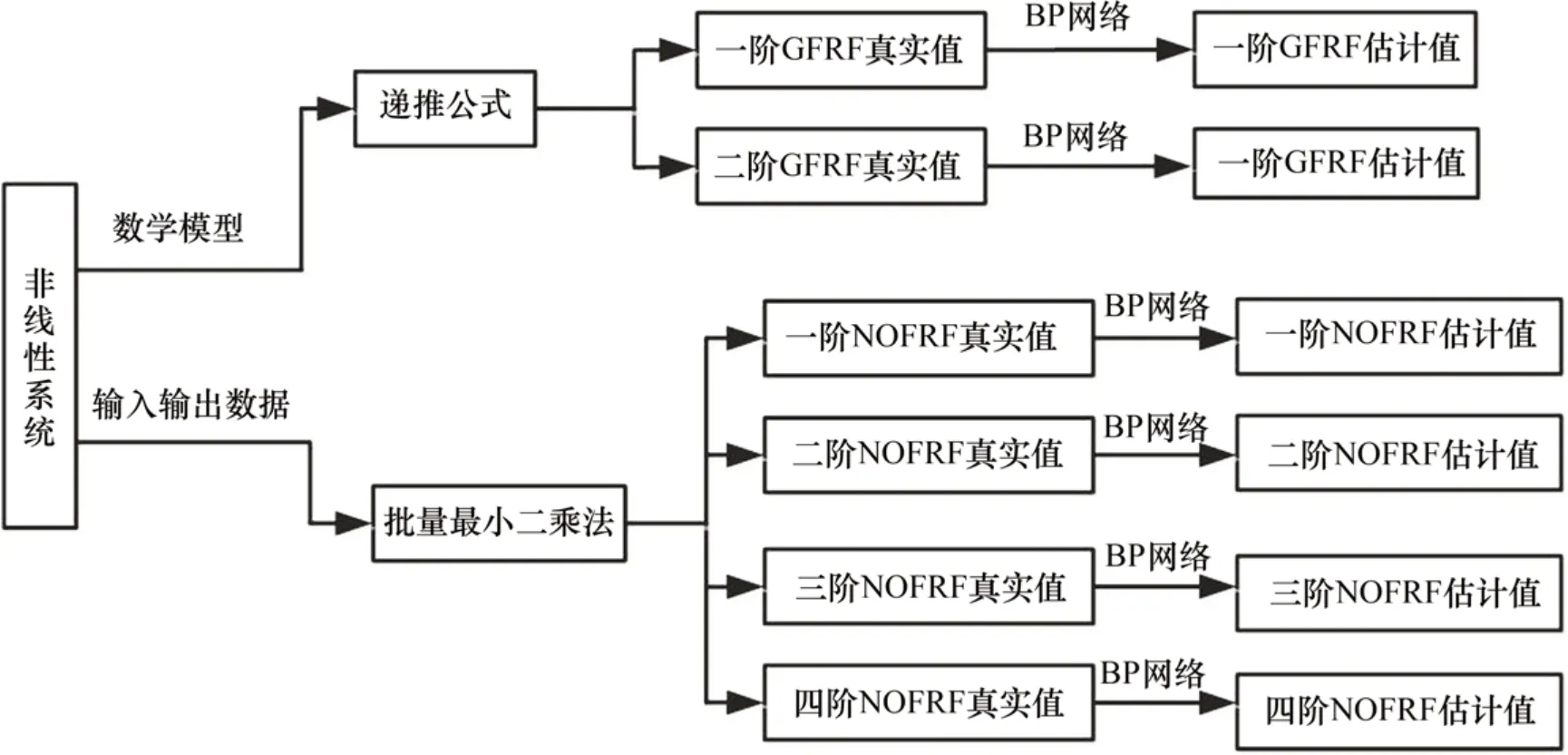
图2 基于BP神经网络的GFRF和NOFRF计算流程Fig.2 GFRF and NOFRF computation based on BP neural network

式中：T为采样间隔时间。

某型号永磁同步电机正常情况下参数为：r=5 Ω，Tl=3 N·m，L=0.005H，φg=0.186 Wb，J=1.5×10-6kg·m2，B=2.0×10-5(N·m·s)/rad，选择采样时间T=0.02 s，根据式(10)，得到系统前2阶GFRF 理论值，然后将GFRF 理论值代入神经网络中进行训练。神经网络隐含层激活函数采用sigmoid 函数，输出层激活函数采用线性函数，误差目标值设置为10-4，学习率设为0.01，最大迭代次数为100，分别运行10次，计算相应的均方根误差ERMSE。当一阶GFRF模型的隐含层神经元个数为10时，ERMSE最小(为0.065 8)；当二阶GFRF模型的隐含层神经元个数为20时，ERMSE最小(为0.007 7)。前2阶GFRF计算结果分别如图3和图4所示。

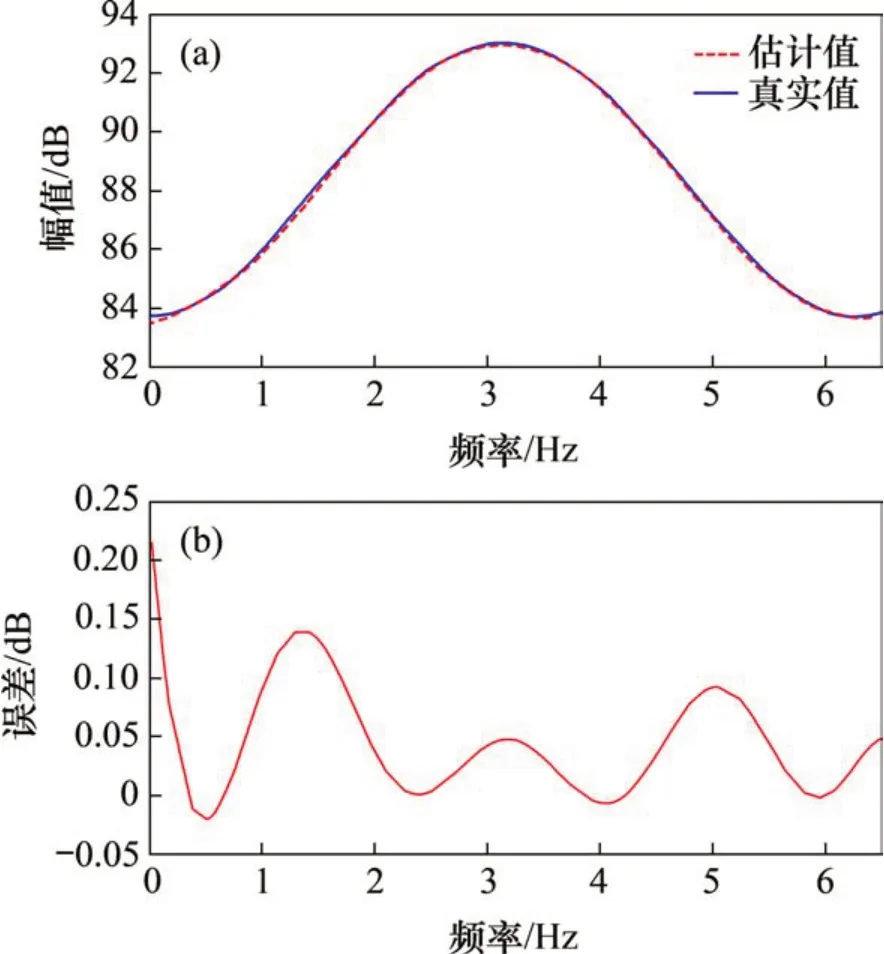
图3 一阶GFRF计算结果Fig.3 Calculation results of first-order GFRF

从图3和图4可以看出：对于GFRF 幅值，一阶GFRF幅值估计值和真实值误差最大为0.216 7 dB；二阶GFRF 幅值估计值和真实值误差最大为0.047 1 dB，由此可见，采用基于BP神经网络方法对GFRF 幅值计算，所得幅值相似度和精确度较高。

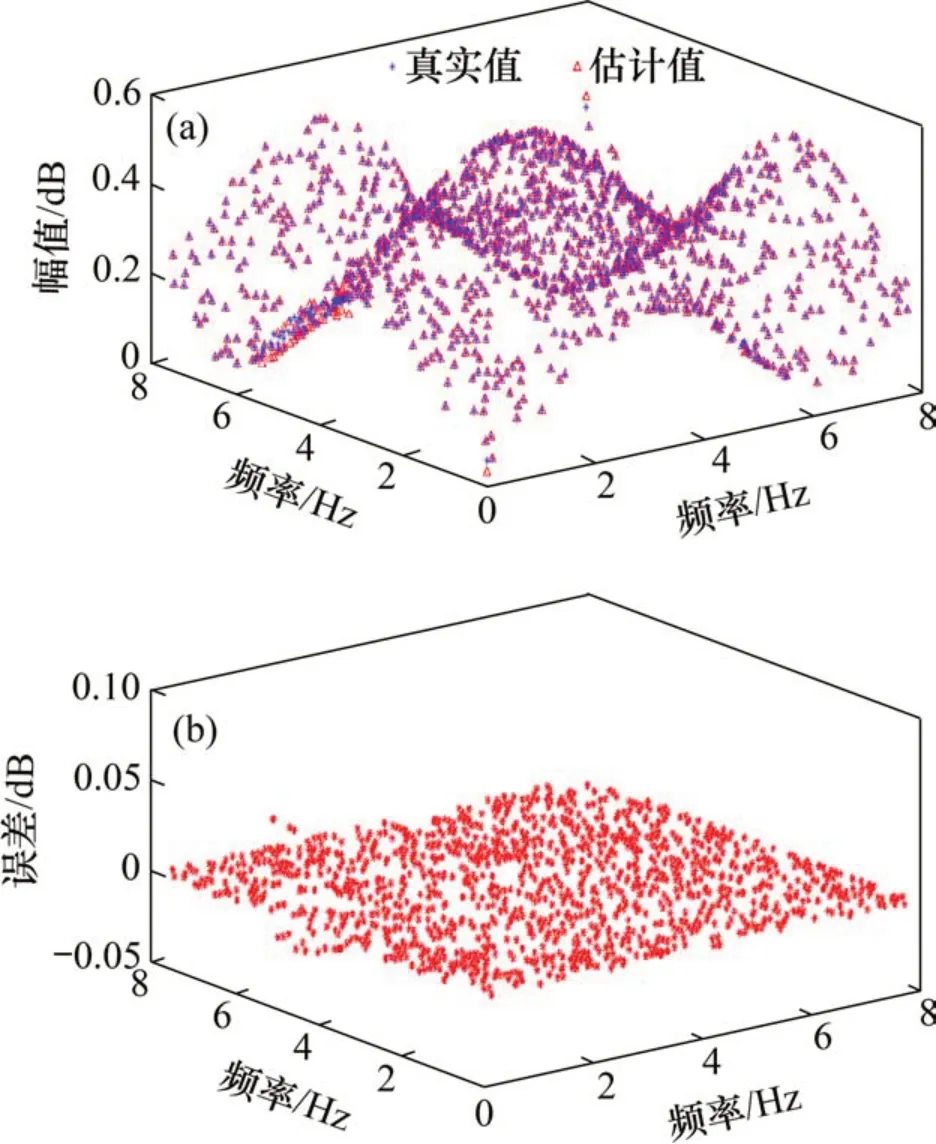
图4 二阶GFRF计算结果Fig.4 Calculation results of second-order GFRF

3.2 NOFRF的智能计算

对于上述工业机器人用永磁同步电机数学模型，采用批量最小二乘算法得到前4 阶NOFRF 幅值，即选择输入信号为：id=Ai×cos(πt)(i=1，2，3，4)；A1=20；A2=25；A3=30；A4=35。采样频率为1 kHz,对系统进行4次激励，得到相应的输出信号，代入式(3)得到前4 阶NOFRF 幅值，然后，将NOFRF 理论值代入神经网络中进行训练，其中，神经网络误差目标值设置为10-6，学习率设为0.02，最大迭代次数为200，分别运行10次，计算相应的均方根误差ERMSE。当一阶NOFRF模型的隐含层神经元个数为30 时，ERMSE最小(为0.040 7)；当二阶NOFRF模型的隐含层神经元个数为30 时，ERMSE最小(为0.132 3)；当三阶NOFRF 模型的隐含层神经元个数为20 时，ERMSE最小(为0.007 6)；当四阶NOFRF模型的隐含层神经元个数为10 时，ERMSE最小(为1.818 2×10-5)。前4 阶NOFRF智能计算结果分别如图5～8所示。

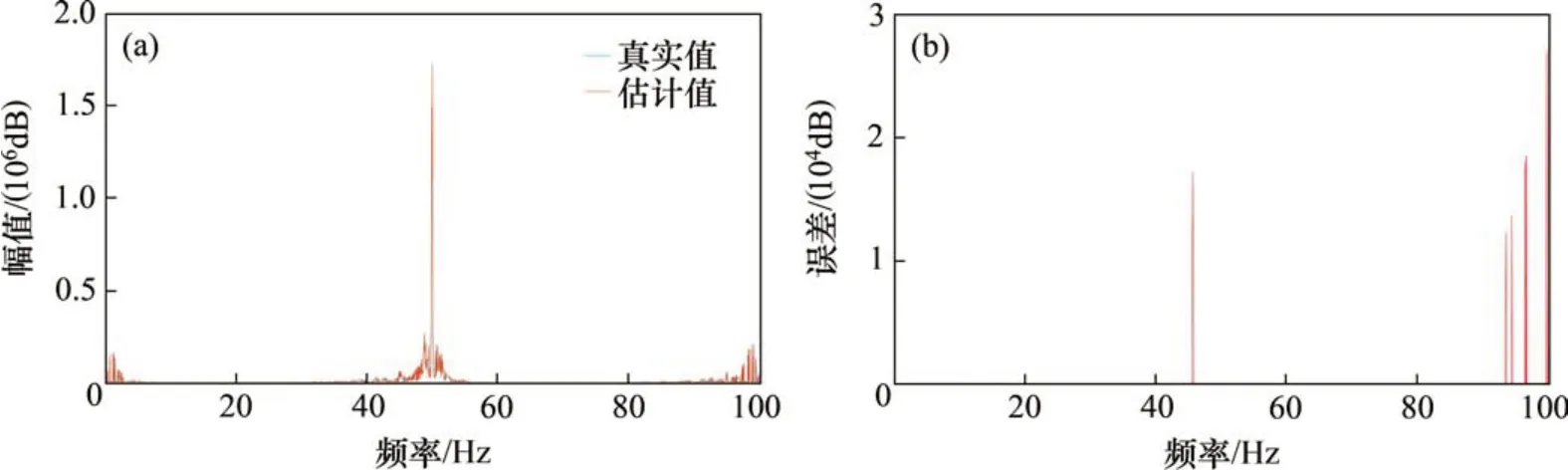
图5 一阶NOFRF幅值Fig.5 First-order NOFRF amplitude

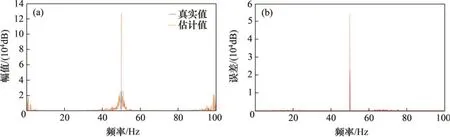
图6 二阶NOFRF幅值Fig.6 Second-order NOFRF amplitude

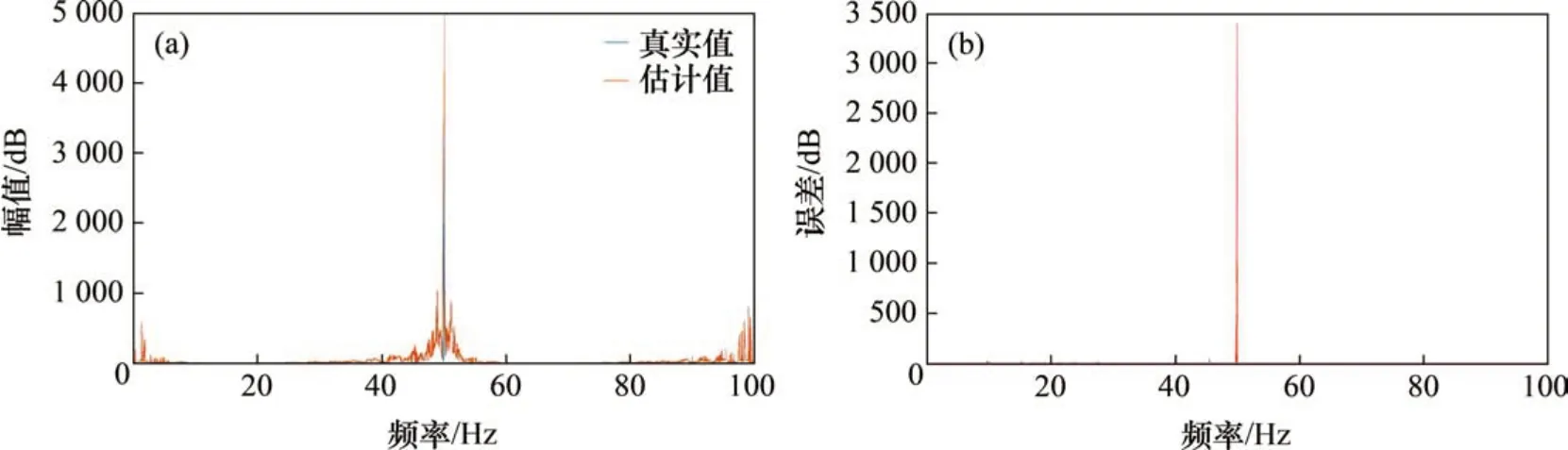
图7 三阶NOFRF幅值Fig.7 Third-order NOFRF amplitude

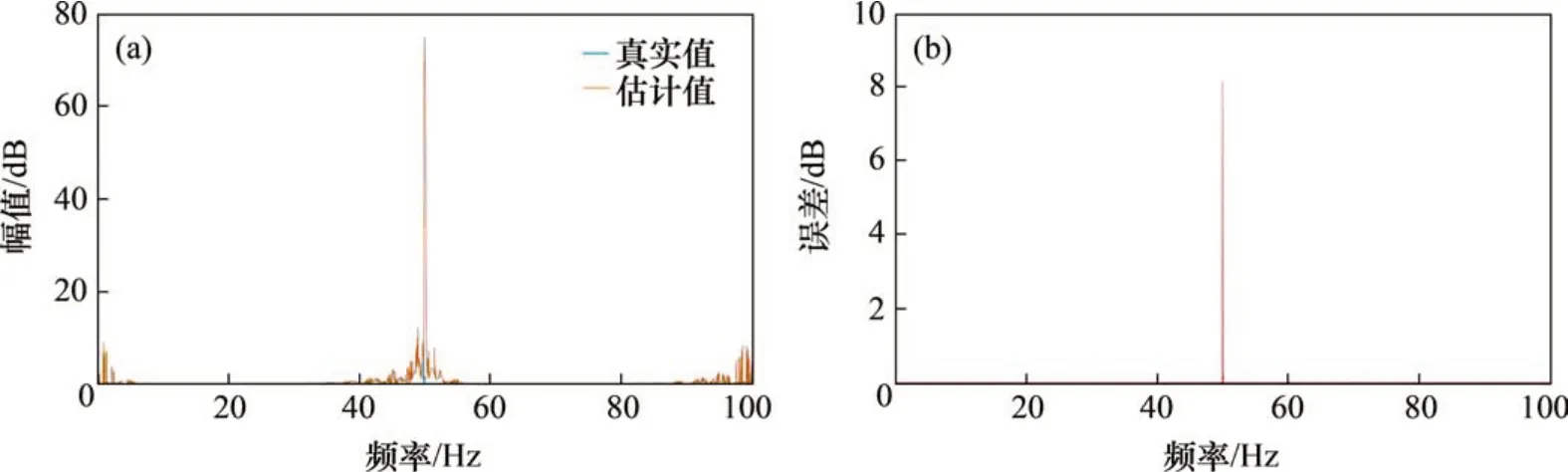
图8 四阶NOFRF幅值Fig.8 Fourth-order NOFRF amplitude

从图5～8可以看出：对于NOFRF幅值的计算，一阶NOFRF 幅值估计值中有1 990 个与真实值一致，准确率达99.50%，最大误差为2.766 0×104dB；二阶NOFRF 幅值估计值中有1 866 个与真实值一致，准确率达93.30%，最大误差为5.424 8×104dB；三阶NOFRF 幅值估计值中有1 972 个与真实值一致，准确率达98.60%，最大误差为3.398 7×103dB；四阶NOFRF 幅值估计值中有1 999 个与真实值一致，准确率达99.95%，最大误差为8.131 4 dB。对于NOFRF 幅值的计算，由于各阶幅值数量级比较大(特别是前3 阶)，会出现个别频点幅值误差比较大的现象，但误差较大的频点数量较少，对计算精度影响有限。在实际操作中，为了提高NOFRF幅值的计算精度和降低计算误差，可以通过增加多音输入函数的组数来实现。

由此可见，利用BP 神经网络对GFRF 幅值和NOFRF 幅值进行估算取得了较高的精度，这一方面与BP神经网络自身强大的数据拟合和特征提取能力有关，另一方面与本文神经元数量选取算法的设计有很大关系，根据非线性频谱特征设计的均方根误差评价指标能够自适应调整网络隐含层神经元数量，避免神经元数量盲目选取，同时又能实现幅值的精确计算。

3.3 自适应辨识方法与传统辨识方法比较

自适应辨识方法是根据系统的实际输出与估计输出偏差值动态调整算法中参数，做到自适应地计算各阶频谱幅值，由于该方法是对各个频点逐一进行计算，与本文方法相比计算效率较低。为了比较两者的计算精度和计算速度，将本文方法分别与最小均方(LMS)自适应算法[18]和变步长最小均方(VSLMS)自适应算法[19]进行比较，以GFRF幅值计算为例，随机选取若干个频点进行计算，计算结果如表1所示。

从表1可以看出：在计算精度方面，采用BP方法对前2阶GFRF幅值进行计算，最小误差绝对值为0 dB，最大误差绝对值为0.077 4 dB；采用LMS方法对前2阶GFRF幅值进行计算，最小误差绝对值为0.011 1 dB，最大误差绝对值为3.338 3 dB；采用VSLMS 方法对前2 阶GFRF 幅值进行计算，最小误差绝对值为0.010 4 dB，最大误差绝对值为1.129 9 dB，可见采用BP方法对幅值进行计算，其估计值比较接近真实值，计算精度较高。在计算效率方面，采用BP 网络完成前2 阶8 个频点的GFRF 幅值估计共耗时359.84 ms；利用LMS 计算方法对8个频点谱值估计共耗时1 352.76 ms，利用VSLMS方法计算8个频点的幅值共耗时992.65 ms，因此，相对于LMS 和VSLMS 方法，采用BP 估计方法计算速度得到提升，分别提高了73.40%和63.75%。

上述2种方法的计算效率和精度差距均较大的原因在于：1)LMS和VSLMS采用逐个频点逐次计算方法，而BP 方法采用批量方式实现多个频点同时计算；2) 在LMS 和VSLMS 方法计算过程中，不收敛的频点会造成该算法陷入局部最优，导致幅值估计值与真实值误差较大，而本文结合非线性频谱特点设计均方根误差指标，通过对幅值估计值和真实值误差进行反馈并指导BP网络进行深度拟合，BP 网络最终得到的估计值和真实值误差较小。

表1 不同方法的GFRF幅值计算结果Table 1 Calculation results of GFRF amplitude with different methods

4 结论

1)采用BP 神经网络，解决了传统方法计算GFRF 幅值和NOFRF 幅值时存在计算复杂和精度低的问题，实现了频谱的智能计算。

2)在利用BP神经网络进行计算过程中，对影响计算精度的激活函数和归一化方法进行分析；同时，结合2 类函数的不同特点，将均方根误差(ERMSE)作为计算结果的评价指标，解决了神经元个数选择的盲目性问题。

3)通过机器人用永磁同步电机仿真验证了所提出方法的有效性。

4)所提出的方法操作简单且计算精度高，对非线性频谱的智能计算具有借鉴意义。