规划阶段建筑冷热负荷预测与特性分析
朱丽,张吉强,王飞雪,孙勇,田玮,朱传琪
(1.天津大学建筑学院,天津,300072;2.天津大学APEC可持续能源中心,天津,300072;3.天津科技大学机械工程学院,天津,300222)
建筑冷热负荷预测是能源规划的重要环节,对能源系统的容量设计和部分负荷运行性能至关重要。在设计运行阶段,人们对建筑负荷预测研究较多,研究方法主要包括基于历史数据的外推法(包括统计回归法、时间序列分析法、机器学习法等)[1-4]和数值模拟预测法[5]等。在规划阶段,人们对建筑负荷预测的研究较少。FERNANDO 等[6]利用蒙特卡罗模拟结合一种简单的集总电容热平衡模型预测了建筑峰值冷负荷。王利珍等[7-8]采用蒙特卡罗法结合负荷计算原理预测了区域建筑冷负荷,计算了区域内峰值冷负荷的频数分布和累积概率,同时,将计算方法应用于典型场景。MACDONALD 等[9]介绍了不确定分析在热模拟程序ESP-r中的应用,并给出了应用实例。已有研究方法在一定程度上解决了建筑信息不确定问题,但繁琐的建模方法和简化的负荷计算原理均给预测结果带来较大误差,为此,本文作者提出一种解决规划阶段预测建筑冷热负荷问题的新方法,并对负荷预测结果进行不确定性和敏感性分析。
1 研究方法
1.1 蒙特卡罗法
蒙特卡罗法(Monte Carlo method)又称统计模拟法,是以概率和统计理论方法为基础的一种计算方法,特别适用于一些解析法难以求解的问题[10]。本文所研究的建筑处于规划阶段,利用蒙特卡罗法能够有效解决该阶段输入参数不确定问题。但蒙特卡罗随机抽样的缺点是收敛速度较慢,这是由其数学性质决定的。而拉丁超立方抽样(Latin hypercube sampling)方法的分层抽样能够加快结果收敛,被广泛应用于建筑能耗分析领域[11]。利用拉丁超立方抽样方法来改善蒙特卡罗法的收敛问题是一种有效途径。基于拉丁超立方抽样的蒙特卡罗模拟方法及结果分析框架如图1所示。

图1 基于拉丁超立方抽样的蒙特卡罗模拟方法及结果分析框架图Fig.1 Frame diagram of Monte Carlo simulation method based on Latin hypercube sampling and result analysis
综合考虑蒙特卡罗法和拉丁超立方抽样的特点,本文采用基于拉丁超立方抽样的蒙特卡罗法对规划阶段建筑冷热负荷进行预测。其基本思路为:在EnergyPlus 软件中建立1 个完整的元模型,提取模型中不确定参数,确定其概率分布与取值范围;利用拉丁超立方抽样方法对不确定参数抽样,形成输入参数样本库;为解决手动逐一建模存在的繁琐和易错问题;利用R语言编辑模型自动生成循环程序,结合EnergyPlus软件的文本编辑接口,将样本参数逐一读入元模型,自动生成与样本对应的模型;将生成的所有模型导入EnergyPlus模拟软件,进行模拟计算并输出模拟结果。
1.2 不确定分析
不确定分析可分为正向不确定分析和逆向不确定分析[12]。本文研究的是正向不确定分析,即评估输入参数的不确定给输出结果带来的不确定性。这种正向不确定传递过程可以描述为:每个不确定输入参数矩阵Xi都服从相应的分布函数Gi,如式(1)所示;通过抽样得到不确定参数矩阵Xi,如式(2)所示;将参数矩阵输入计算模型得到对应的输出结果Y,如式(3)所示[13]。常用的不确定性统计指标包括均值、分位数、标准差、置信区间等,常用于表示不确定性的图形有直方图、箱线图、概率密度函数图以及累积概率分布图等。

式中:Gi为分布函数;Xi为输入参数矩阵;Y为模型输出矩阵;n为参数个数;“~”表示“服从”。
1.3 敏感性分析
敏感性分析是研究模型输入不确定如何影响模型输出的方法,可分为局部敏感性分析和全局敏感性分析[14]。全局敏感性方法可以探索多参数共同变化下各参数自身及参数间交互作用对模型输出的影响。本文采用标准回归系数(CSR)敏感性分析方法和树状高斯过程模型(TGP)敏感性分析方法研究输入参数对输出结果的影响,这2种方法分别在R 语言平台“sensitivity”包中“SRC”函数和“TGP”包中“Sen”函数中实现。
标准回归系数CSR敏感性分析方法适用于线性模型,对于大量数据,计算成本小。由于不同参数的取值范围不同,采用回归系数不便于比较相对重要性,需要将其转化为标准回归系数。通过CSR绝对值可以判断参数对能耗影响的相对敏感性,CSR绝对值越大,则参数越重要。若参数为正值,则表示参数与模型输出呈正相关;若参数为负值,则表示参数与模型输出呈负相关[15]。标准回归系数计算公式为

式中:βi为第i个参数的回归系数;CSRi为第i个参数的标准回归系数;σy为模型输出总标准差;σi为第i个参数的标准差。
TGP 敏感性分析方法适用于非线性和非静态回归模型,但计算成本较高。TGP有2个敏感性指标,即主效应和全效应。主效应指各参数独自作用引起输出结果的方差与输出总方差的比值,全效应指各参数及与其他参数交互作用下引起的输出结果的方差与输出总方差的比值[16],具体公式如下:

式中:Si为主效应;Ti为全效应;Xi为输入参数;X~i为不包括Xi的其余参数;Y为模型输出;E为期望;V为方差。
2 案例研究
2.1 项目概况
以天津地区某规划用地为研究案例,采用基于拉丁超立方抽样的蒙特卡罗法对该地块拟建建筑冷热负荷进行建模模拟。已知该规划用地拟建1栋办公建筑,用地面积为6 000 m2,容积率为6,建筑密度为0.4,限高为160 m。
2.2 蒙特卡罗模拟
对该办公建筑建立蒙特卡罗模拟模型。根据提供的规划信息,计算得到办公建筑面积为36 000 m2。通过场地分析,并参考办公建筑设计标准[17],将建筑模型主入口设计为正南方向;标准层设计为矩形,每层划分为东、西、南、北、中共5个区,中区为核心筒,层高设定为4 m[18]。
蒙特卡罗模拟模型中包括确定性参数和不确定参数,其中确定性参数如表1所示[19]。本案例中涉及10 个建筑本体不确定参数,其可归类为认知不确定参数[12]。这些参数值的选择与设计师对现行标准规范、气候条件、人文风俗等的认知以及长期积累的经验密切相关,不同设计师的认知水平和经验不同,但均要遵循现行标准规范,因此,这10 个建筑本体不确定参数的主要选择依据是现行标准规范,同时需要考虑设计师的认知水平和经验,这主要体现在对当地既有同类建筑的调研结果上。10个建筑本体不确定参数具体选择如表2所示[13,19-20]。
通常抽样数量与抽样方法和变量个数密切相关,为确保样本收敛效果更好,采用拉丁超立方抽样方法对模型中10 个建筑本体不确定参数抽取2 000个样本[21-22]。结合EnergyPlus软件在R语言环境中编程并自动生成2 000个模型,以组的形式将2 000 个模型导入EnergyPlus 软件,模拟计算建筑冷热负荷。图2所示为研究案例中模型的编程、生成、模拟和输出结果流程图。
3 结果分析
3.1 不确定分析
峰度系数(kurtosis)表征数据分布峰态相较于正态分布的高尖和矮宽程度,偏度系数(skewness)表征数据分布形态的对称性,正态分布的峰度系数和偏度系数均为0。图3所示为基于2 000组模型的峰值冷负荷不确定分析结果。经计算,单位面积峰值冷负荷峰度系数为2.6,相较于正态分布峰态高尖;偏度系数为-0.11,形态不对称,这与图3(a)中概率密度曲线相吻合。采用Quantile-Quantile图(Q-Q图)来验证数据是否服从正态分布,若散点图近似为1条对角直线,则说明数据服从正态分布。如图3(c)所示,其中,中间的负荷曲线非常接近实线,而两端的负荷曲线与实线有较大偏差,这表明单位面积峰值冷负荷并不完全服从正态分布。
2 000组模拟数据的单位面积峰值冷负荷均值为65 W/m2,标准差为11.8 W/m2;最大值、最小值以及其他分位数如图3(b)所示。单位面积峰值冷负荷的区间概率可以直观地从累积概率分布得到。从图3(d)可见:单位面积峰值冷负荷在53.4~76.7 W/m2(AB区间)的概率为68%;在99%的置信度下,单位面积峰值冷负荷值为92.1 W/m2(图中C点)。理论上,单位面积峰值冷负荷超过97 W/m2的概率为0。

表1 模型确定性参数Table 1 Model certainty parameters
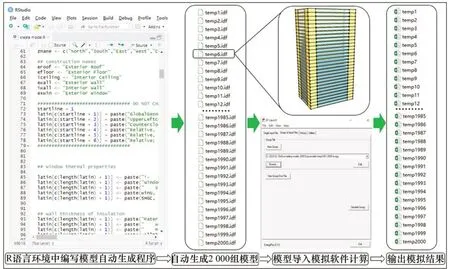
图2 研究案例中模型的编程、生成、模拟和输出结果流程Fig.2 Flow chart of programming,generating,simulating and exporting results of model in research case
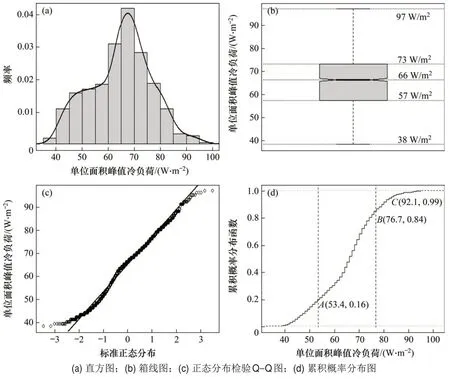
图3 单位面积峰值冷负荷不确定分析Fig.3 Uncertainty analysis of peak cooling load per unit area
图4所示为基于2 000 组模型的峰值热负荷不确定性分析结果。通过计算可得单位面积峰值热负荷的峰度系数为2.5,与正态分布相比峰态高尖;偏度系数为-0.07,形态不对称,这与图4(a)中概率密度曲线相吻合。从图4(c)可见:单位面积峰值热负荷中间值非常接近实线值,而两端的负荷与实线值有较大偏差,这表明单位面积峰值热负荷并不完全服从正态分布。
2 000组模拟数据的单位面积峰值热负荷均值为40.2 W/m2,标准差为5.6 W/m2。图4(b)所示为单位面积峰值热负荷最大值、最小值以及其他分位数。单位面积峰值热负荷的区间概率可以直观地从累积概率分布图中得到。从图4(d)可见:单位面积峰值热负荷值在34.7~45.8 W/m2(AB区间)的概率为68%;在99%的置信度下,单位面积峰值热负荷值为53.2 W/m2(图中F点)。理论上,单位面积峰值热负荷超过56 W/m2的概率为0。
3.2 敏感性分析
图5所示为单位面积峰值冷热负荷标准回归系数CSHG敏感性分析结果。从图5(a)可见:太阳得热系数CSR对单位面积峰值冷负荷的影响最大,南向窗墙比Rw、北向窗墙比Rc和建筑底面长宽比RA紧随其后,屋顶传热系数Uf、外墙传热系数Uow和外窗传热系数Uw影响最小;外窗传热系数Uw与单位面积峰值冷负荷呈负相关关系,其他参数都与之呈正相关关系。从图5(b)可见:外窗传热系数Uw对单位面积峰值热负荷的影响最大,建筑层数NF和建筑底面长宽比RA影响次之,屋顶传热系数和太阳得热系数影响最弱;除了太阳得热系数与单位面积峰值热负荷呈负相关外,其他参数都与之呈正相关。图6和图7所示分别为单位面积峰值冷热负荷TGP 敏感性分析结果。从图6和图7可见:各参数和输出结果的相关性与标准回归系数CSR分析结果一致;各参数的重要性排序与CSR分析结果大致相同。这2种全局敏感性分析方法的分析结果得到了相互验证,说明敏感性分析结果是可靠的。
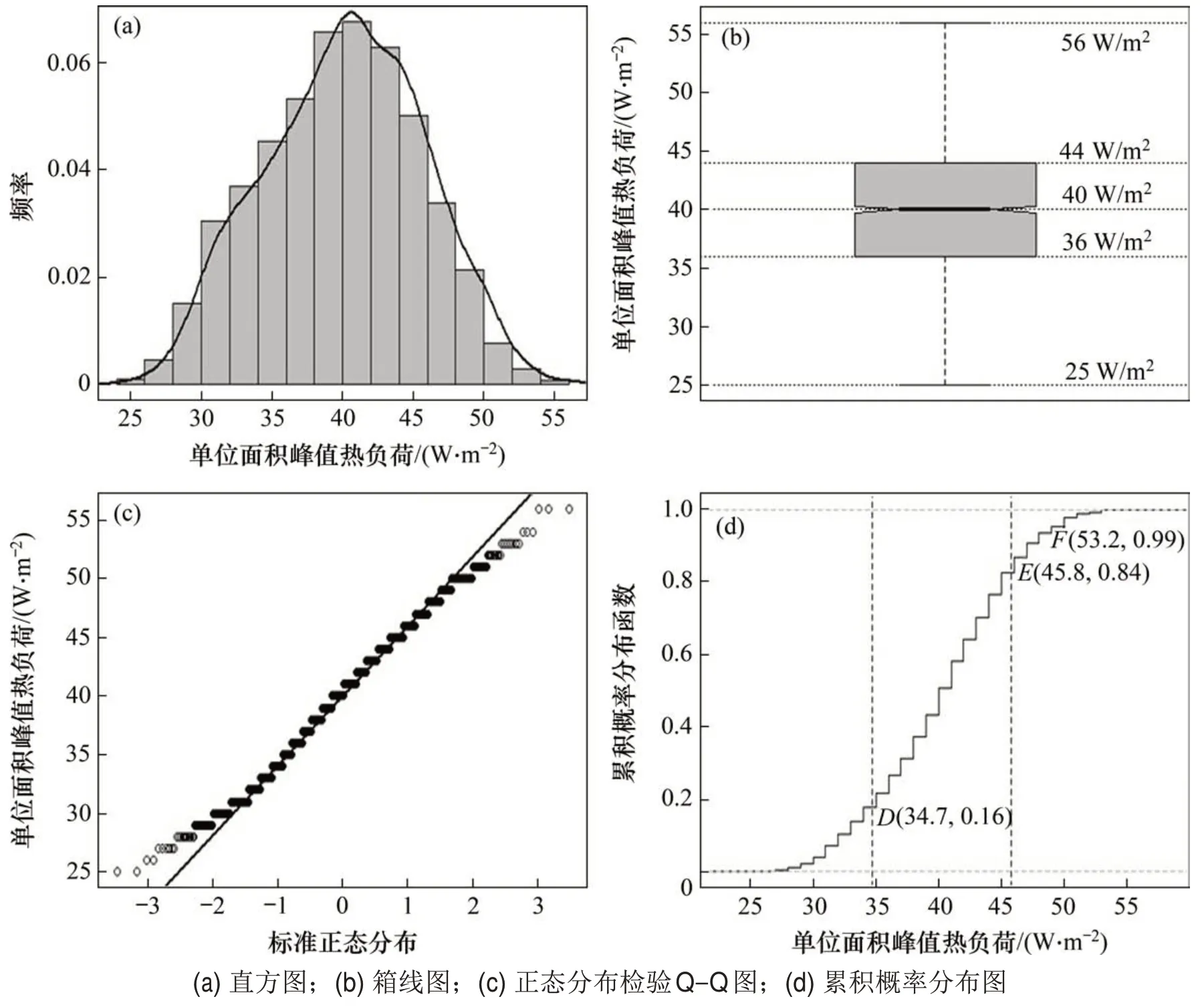
图4 单位面积峰值热负荷不确定分析Fig.4 Uncertainty analysis of peak heating load per unit area
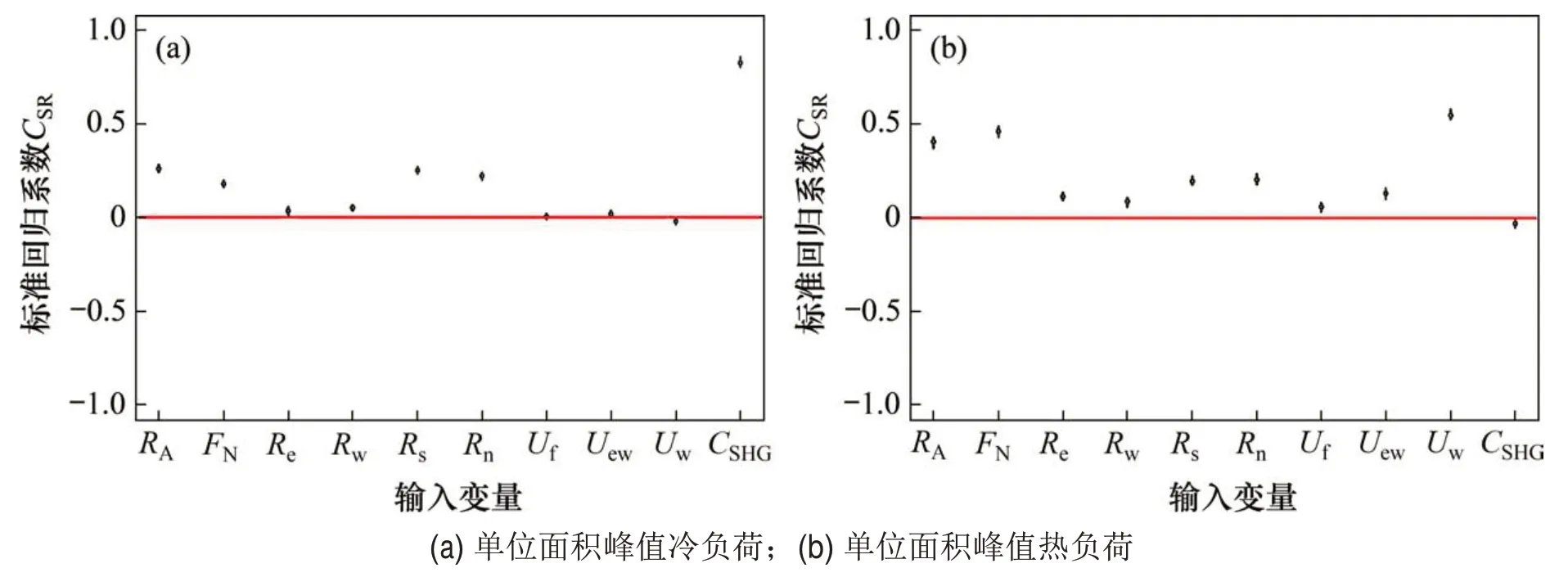
图5 标准回归系数CSR敏感性分析Fig.5 Sensitivity analysis of CSR
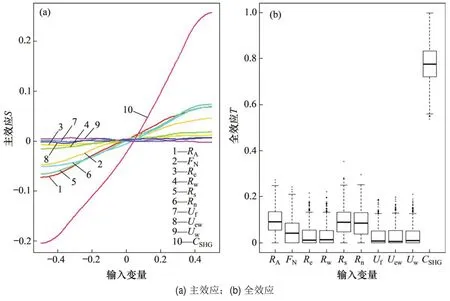
图6 单位面积峰值冷负荷TGP敏感性分析Fig.6 TGP sensitivity analysis of peak cooling load per unit area
太阳得热系数对单位面积峰值冷负荷的影响最大,而对单位面积峰值热负荷的影响最小,外窗传热系数却与之截然相反。而建筑层数、建筑底面长宽比、南向窗墙比和北向窗墙比对单位面积峰值冷热负荷的影响均较大,屋顶传热系数、外墙传热系数、东向窗墙比和西向窗墙比对单位面积峰值冷热负荷的影响均较小。因此,要着重考虑太阳得热系数、外窗传热系数、建筑层数、建筑底面长宽比、南向窗墙比和北向窗墙比这6个参数的取值范围,在符合现行标准规范的同时,应根据实际规划用地和当地建筑热工现状适当缩小其阈值,提高建筑负荷预测精度。屋顶传热系数、外墙传热系数、东向窗墙比和西向窗墙比对单位面积峰值冷热负荷影响均较小,这4个参数的阈值可以不通过实地调研的方式确定,可根据现行标准规范设定。
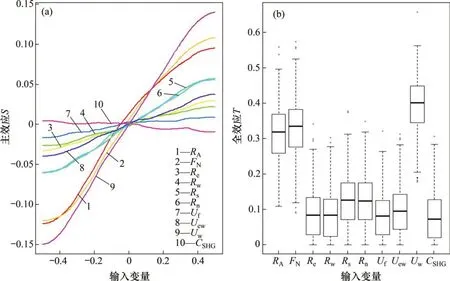
图7 单位面积峰值热负荷TGP敏感性分析Fig.7 TGP sensitivity analysis of peak heating load per unit area
4 结论
1)基于拉丁超立方抽样的蒙特卡罗模拟方法充分利用分层抽样的优势,实现了抽样结果的快速收敛,使输入数据的假设更加合理化,解决了建筑参数的不确定和未知性问题。
2)该方法结合EnergyPlus 软件的文本编辑接口,利用R 语言编辑模型自动生成程序,实现了EnergyPlus模型的快速生成,解决了手动逐一建模的繁琐和易错问题,大大降低了负荷预测建模耗时。
3)太阳得热系数、外窗传热系数、建筑层数、建筑底面长宽比、南向窗墙比和北向窗墙比这6个参数对建筑冷热负荷预测结果影响显著,因此,为提高规划阶段建筑冷热负荷预测精度,在符合现行标准规范的条件下,应根据实际规划用地和当地建筑热工现状适当缩小其阈值。
4)得到应用案例建筑的峰值冷热负荷概率分布和特征值,其中单位面积峰值冷热负荷在53.4~76.7 W/m2和34.7~45.8 W/m2的概率为68%,单位面积峰值冷热负荷均值分别为65 W/m2和40.2 W/m2,标准差分别为11.8 W/m2和5.6 W/m2。5)本文提出的基于拉丁超立方抽样的蒙特卡罗模拟方法能够有效解决规划阶段建筑冷热负荷预测问题,有助于规划设计安全但不太保守的系统,从而能够控制风险决策和投资成本,为区域建筑能源规划提供一种新的思路。
——以嘉兴市为例

