煤体应力对钻进切削力的影响

赵志刚，邱东卫，杨坤，郑雅华

(1.山东科技大学能源与矿业工程学院，山东青岛，266590；2.山东科技大学矿山灾害预防控制省部共建国家重点实验室培育基地，山东青岛，266590)

在矿井煤层开采过程中，为保证开采的安全性，需要采取大量的安全措施，而这些措施大部分需在煤层中钻孔。煤层钻孔作为一种基本方法在众多矿井安全技术中得以应用，就冲击地压防治的卸压方式而言，就有大直径钻孔卸压、煤层注水卸压、煤体爆破卸压等。已有研究表明，煤层钻孔过程会受到井下工程地质条件和煤体应力的影响，而钻孔过程中的主要破煤方式为切削煤体，因此，研究钻孔过程中的切削力与煤体应力的关系显得尤为重要。针对切削力和岩体应力的关系，学者们采用理论分析、实验研究和数值模拟的方法进行了大量研究。马清明等[1]采用摩擦接触有限元的分析方法，研究了金刚石复合片钻头(PDC)切削齿的负前角、切削深度等对切削齿和岩石受力的影响规律；KAITKAY 等[2]通过实验测试了围压对大理岩切削力的影响，发现在围压条件下大理岩的切削力明显增加，但并没有深入分析切削力增加的原因；张魁等[3-4]采用离散单元方法，研究了不同围压条件下隧道掘进机(TBM)刀具对岩石的侵入破坏，模拟了岩石裂纹生成、扩展和岩石破碎过程，发现随着围压的增加，刀具的破岩效率与裂纹扩展能力降低，但未对刀具受力进行研究；李田军[5]采用理论分析、实验研究和仿真分析相结合的方法，研究了PDC 切削齿在双向荷载作用下钻进岩石时，岩石破碎前的裂纹萌生与破裂面位置，建立了岩石切削破坏条件的理论模型；祝效华等[6]基于D-P准则，建立了PDC切削齿破岩的三维有限元模型，分析了围压对破岩能效的影响，给出了不同围压下砂岩的切向力与切削齿后倾角的关系曲线和切向力随时间变化的波动曲线；李艳等[7-9]采用理论分析和数值模拟相结合的方法研究了在高海水围压条件下截齿切削多金属硫化物的动力学特性，构建了镐形单截齿的切削力数学模型，利用有限元法模拟了多金属硫化物的切削破碎过程，给出了不同围压条件下截割阻力、进给阻力、侧向阻力随时间的周期波动曲线。目前，尽管关于切削力和煤岩体应力关系的研究较多，但一方面，在大部分的理论分析中，人们对岩体应力对切削力影响规律的研究尚少，且将应力作为独立参量，给出应力与切削力关系的直观关系式的研究相对较少；另一方面，直接针对切削力与煤体应力关系的研究相对欠缺。因此，本文作者基于摩尔-库仑强度准则，采用理论分析和数值模拟相结合的方法，分别建立钻刃切削煤体的静力学和离散元模型，研究煤体应力对切削力的影响规律。

1 钻头转动切削煤体的静力学分析

1.1 钻刃切削煤体机理

在钻孔过程中，钻头在轴向推力作用下侵入煤体后，在钻杆扭矩带动下侧向转动挤压煤体。钻头两翼的转动切削力形成1对力偶，与轴向推力合成力螺旋，煤体在力螺旋作用下发生轴向压缩破坏和环向剪切破坏，产生的煤粉由麻花钻杆转动带出钻孔。钻头在力螺旋驱动下，其运动轨迹为螺旋线，轴向推力和转动切削力是独立参数，钻头螺旋运动可分解为沿孔轴线的直线运动和沿垂直孔轴线的圆周运动[10]。

基于室内钻孔试验研究和现场施工响应可知：深部巷道煤层钻孔时，随着煤体应力的增大，钻机钻孔所需能耗增加，当钻孔孔底接近煤壁支承压力峰值位置时，常常出现卡钻、顶钻甚至扭断钻杆现象。煤体应力会对钻头钻进产生影响，进而影响切削力[11-12]。

经煤体切削实验发现，切削力随切削长度呈现明显周期变化。1 次完整的切削过程可以表述为：钻刃转动挤压煤体，切削力随着煤体压缩变形呈线性增加，达到一定数值后，小块煤体被破碎抛出，钻刃局部与煤体脱离接触，切削力快速下降；随钻刃继续转动，切削力重新上升；切削力小幅下降再上升，该过程重复多次后，切削力达到峰值，大块煤体被破坏抛出，切削力突然下降到零附近，之后又开始新一轮转动切削。钻刃转动切削煤体时，要克服煤体抗力、钻刃与煤体的摩擦力以及煤体应力产生的抵抗力。

1.2 钻刃切削煤体静力学模型

在钻头钻进破煤的过程中，轴向推进力将钻头压入煤体，电机驱动钻杆转动产生转动切削力，钻刃受到的力包括轴向推力FN、转动切削力Fq、煤体水平方向抗力Fk、煤体轴向反力Fh、煤体应力附加力Fσ0，如图1所示。

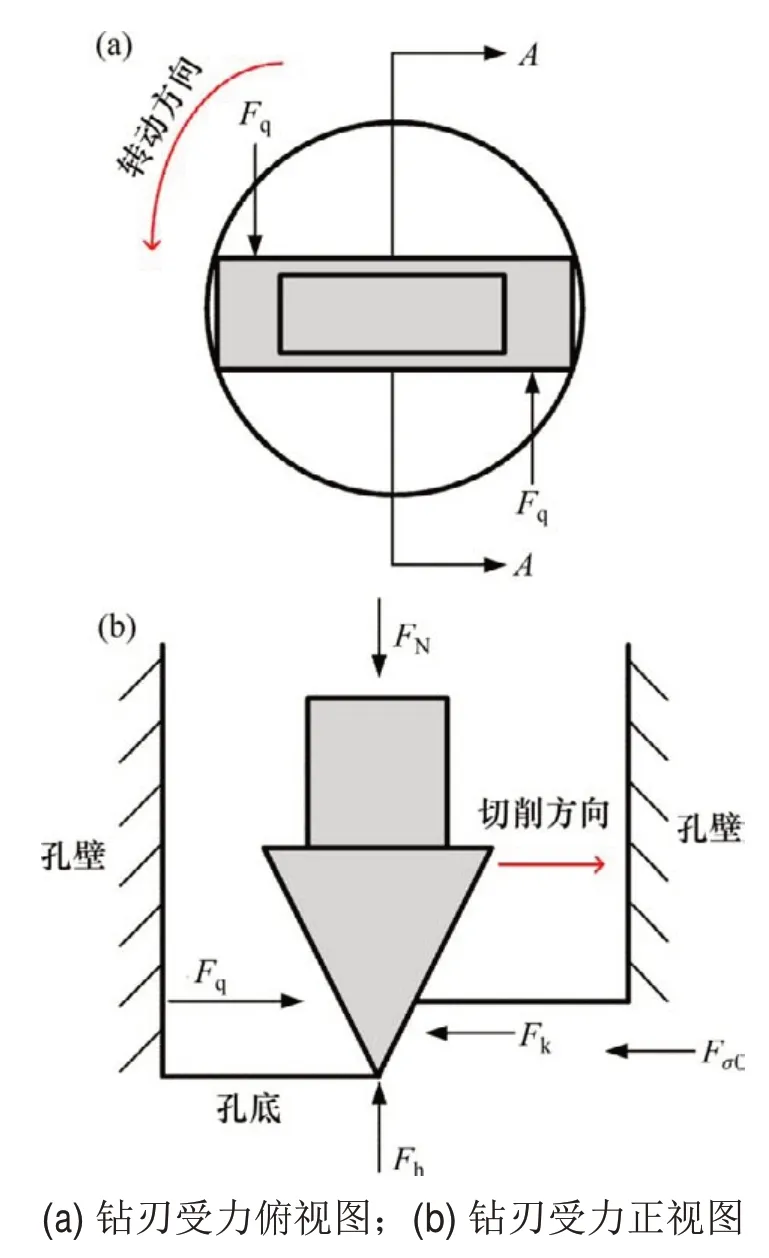
图1 钻刃受力模型图Fig.1 Drill blade force model

为分析钻刃破坏煤体过程，采用如下假设：

1)煤体均质、各向同性。顺煤层钻孔发生在同一层煤中，假设沿钻孔深度方向煤体力学性质不变，不考虑钻头本身的重力。

2)考虑到孔径远大于压入深度，假设煤体受力为平面应力状态。

3)由文献[10]可知，切削煤体时前刃面上的最大压力位于钻刃前方距离很小的位置处，并随钻刃距离增加而迅速减小，因此假设煤体抗力为集中力，代替钻刃上实际作用的分布力。

4)破裂面为直线，破裂面上的正应力、切应力均匀分布。

5)忽略钻头底部与孔底煤体摩擦力以及钻头侧面与孔壁煤体摩擦力。

6)煤体破坏符合摩尔-库仑强度准则。

根据以上假设，可知切削力等于煤体抗力与煤体应力产生的附加力的合力，建立钻刃转动切削煤体静力学模型，如图2所示，其中，h为切削深度，θ为钻刃半角，L为破裂面长度，α为破裂面倾角。

图2 钻刃切削力、煤体抗力、煤体应力关系Fig.2 Relationship between cutting force of drill edge,coal body resistance and coal body stress

钻头侧面受到切削力Fq、刀具切削时煤体的抗力Fk、煤体应力附加力Fσ0这3个力的作用，有

煤体应力附加力为

式中：b为钻刃的宽度；σ0为煤体应力。

将煤体抗力Fk分解为钻刃面的法向力N和切向力W，则有

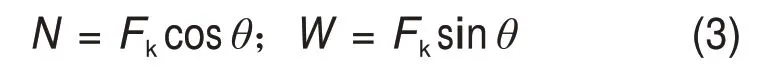
钻刃与煤体紧密接触，煤体受到钻刃反作用的法向力N1和切向力W1，将N1分解为破裂面法向力NR和切向力NS：

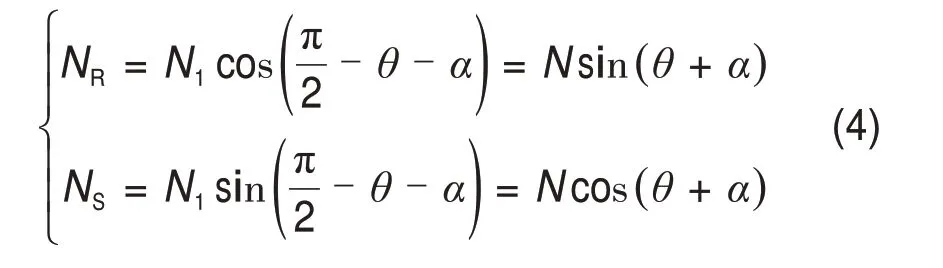
将W1分解为破裂面法向力WR和切向力WS，如图3所示。

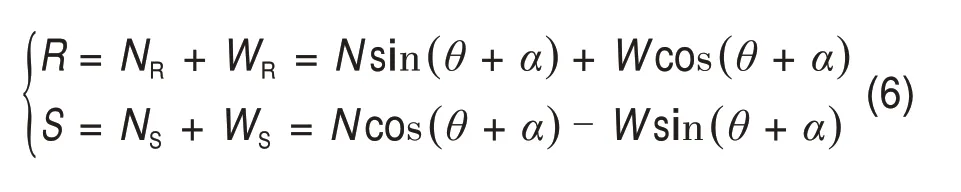
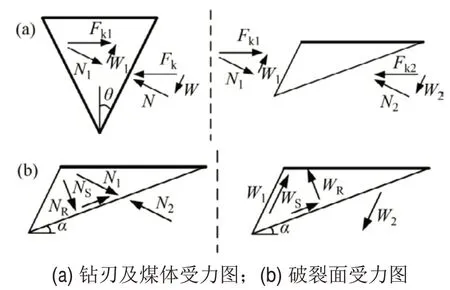
图3 钻刃及煤体剪切破裂面受力分解示意图Fig.3 Mechanical decomposition diagram of drill edge and coal shear fracture surface

煤体破裂面上作用的正应力σ和剪应力τ分别为：

煤体沿破裂面剪切破坏，假设破坏条件符合摩尔-库仑强度理论，则有

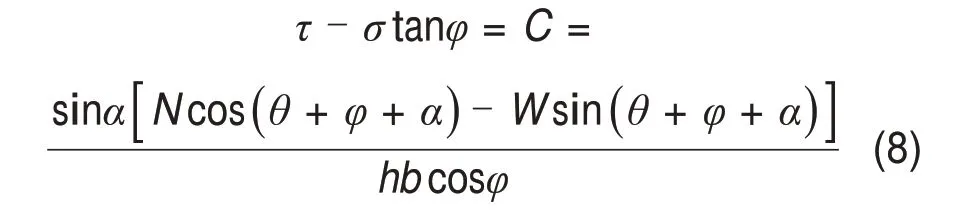
式中：C为煤的黏聚力；φ为内摩擦角。

由式(8)可见：τ-σtanφ是破裂面倾角α的函数，对式(8)中α求导并令其为零可以获得τ-σtanφ的极值。

将式(3)代入式(9)并整理可得

因当0<α< π/2 时，(τ-σtanφ)″< 0，则τ-σtanφ存在极大值。令式(10)为0 可得：2θ+φ+2α=π/2，则破裂面倾角α为

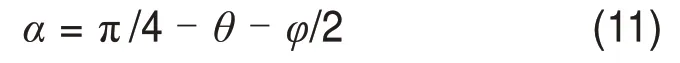
将式(11)代入式(8)可得

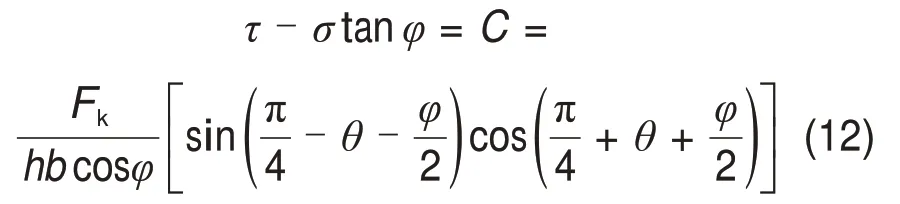
整理后可得到煤体抗力的峰值Fk,p为

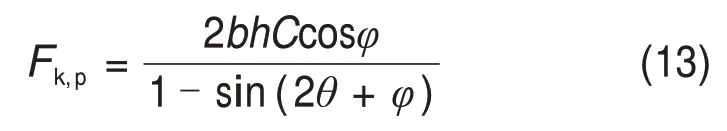
结合式(1)和式(2)可得切削力峰值Fq,p为

由表1 的极差分析结果可知，各因素对结果的影响主次顺序为：有机酸添加量>三聚磷酸钠添加量>焦亚硫酸钠添加量。大豆制品护色技术的最优方案为灭菌工艺105 ℃、8 min，柠檬酸与乳酸的添加比例为3∶1，焦亚硫酸钠的添加量为0.03%，三聚磷酸钠的添加量为0.10%。

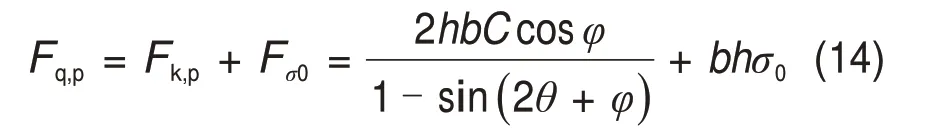
2 切削力影响因素分析

2.1 煤体应力对切削力的影响

为分析煤体应力对切削力的影响规律，对切削力计算公式(14)中的切削深度h分别取1，2 和3 mm，钻刃侧面宽度b取6 cm，内摩擦角φ取40°，钻刃半角θ取7.5°，绘制煤体应力与切削力关系曲线，如图4所示。

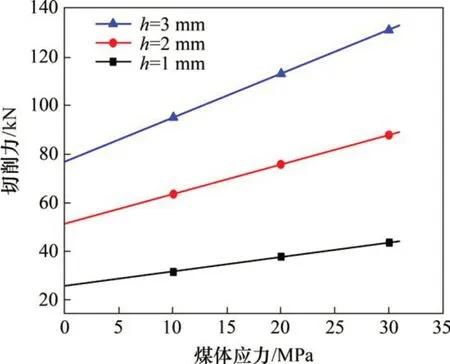
图4 煤体应力与切削力关系曲线Fig.4 Relationship curves of coal body stress and cutting force

由图4可见：煤体应力与切削力呈线性关系，煤体应力越大，切削力越大；随着切削深度增加，煤体应力-切削力斜直线的斜率随之增大。

2.2 钻刃半角对切削力的影响

为分析钻刃角度对切削力的影响，对式(14)中的切削深度h取1 mm，钻刃侧面宽度b取6 cm，黏聚力C取5 MPa，内摩擦角φ取40°，绘制煤体应力分别为10，15和20 MPa时钻刃半角与切削力的关系曲线，如图5所示。由图5可见：当θ<25°时，切削力随着钻刃半角的增大而增大；当θ等于25°时，2θ+φ趋近于90°，破裂面角α趋近于0，破裂面无限长，切削力无限大，煤体破坏不再是剪切破坏而将转变为压缩破坏；当θ<20°时，切削力几乎不随刃角变化，采用尖锐钻头并不能降低切削力，反而容易造成钻刃磨损。在实践中，可以采用钻刃半角为20°的钻头，既能以较小的切削力破煤，又能延长钻头使用寿命。

图5 钻刃半角与切削力关系曲线Fig.5 Relationship curves of half angle of drill edge and cutting force

2.3 切削深度对切削力的影响

式(14)中钻刃侧面宽度b取6 cm，内摩擦角φ取40°，钻刃半角θ取7.5°，绘制煤体应力分别为10，15和20 MPa时不同切削深度与切削力关系曲线，如图6所示。

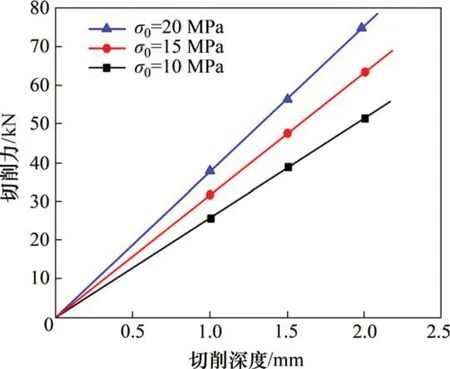
图6 切削深度与切削力关系曲线Fig.6 Relationship curves of cutting depth and cutting force

由图6可见，切削深度与切削力呈线性关系，在其他参数不变的情况下，切削深度越大切削力越大；在相同切削深度条件下，煤体应力越大，切削力越大，且应力较大的斜直线斜率大于应力较小的斜直线斜率。这表明应力较大时，切削力增加幅度更大，这与图4所示规律一致。

3 切削离散元模型

3.1 模型建立

颗粒流程序(particle flow code, PFC)是在离散元理论和显式差分法的基础上开发的离散元程序[13-15]，可以从细观层面模拟煤体颗粒的黏结和破坏，对研究煤体裂纹发展机理和破坏全过程具有一定作用。本文使用PFC-2D模拟软件对钻刃切削煤体的过程进行模拟[16-17]。

采用平面黏结模型来对煤体试件进行模拟及细观参数的标定，煤的细观物理力学参数[18-20]取值如表1所示。利用表1中参数可计算得到试样颗粒流模型的宏观力学参数。表2所示为颗粒流模拟的煤体力学参数与室内试验的力学参数对比，图7所示为模拟的破裂模式与试验破裂模式对比。从模拟结果和试验结果可以看出：煤样力学特性基本一致，表明参数选取较合理并可用于后续建立切削离散元模型对切削过程计算分析。

表1 煤标准试件的细观物理力学参数Table 1 Meso-physical and mechanical parameters of coal standard specimens

表2 煤样标准试件力学参数对比Table 2 Comparison of mechanical parameters of standard coal samples

为便于分析，将钻刃旋转切削简化为平面直线切削，建立二维的煤体切削模型，如图8所示。煤体试件模型的长和宽分别为0.2 m和0.1 m。综合考虑运算速度和运算精度，模型分2层：上层为切削层，颗粒半径取0.30～0.48 mm；下层为非切削层，颗粒半径取1.80～2.88 mm。共包含18 971 个颗粒，切削墙以0.2 m/h的水平切削速度切削试件，通过在钻刃切削方向施加不同围压模拟不同的煤体应力，进而分析切削力与煤体应力的关系。

图7 试件破裂模式对比Fig.7 Comparison of fracture patterns of specimens

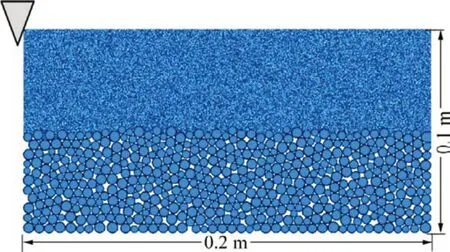
图8 切削数值模拟模型Fig.8 Cutting numerical simulation model

3.2 煤体应力对裂纹的影响

选取煤体应力为20 MPa 条件下的切削方案，分析切削过程中裂纹扩展规律。图9所示为切削位移从2 mm增加到12 mm时的裂纹扩展情况。由图9可见：当切削开始时，钻刃向右移动对煤体试件产生挤压，煤体试件出现细微裂纹；随着钻刃不断地向右移动，细微裂纹开始扩展成主裂纹时，切削力达到第1个峰值，接着，煤体试件开始顺着主裂纹破坏脱落，切削力下降。整个切削过程即为上述过程的循环，因此，在不同煤体应力下，裂纹扩展情况和数量变化可用来反映煤体应力对煤体破坏的影响。

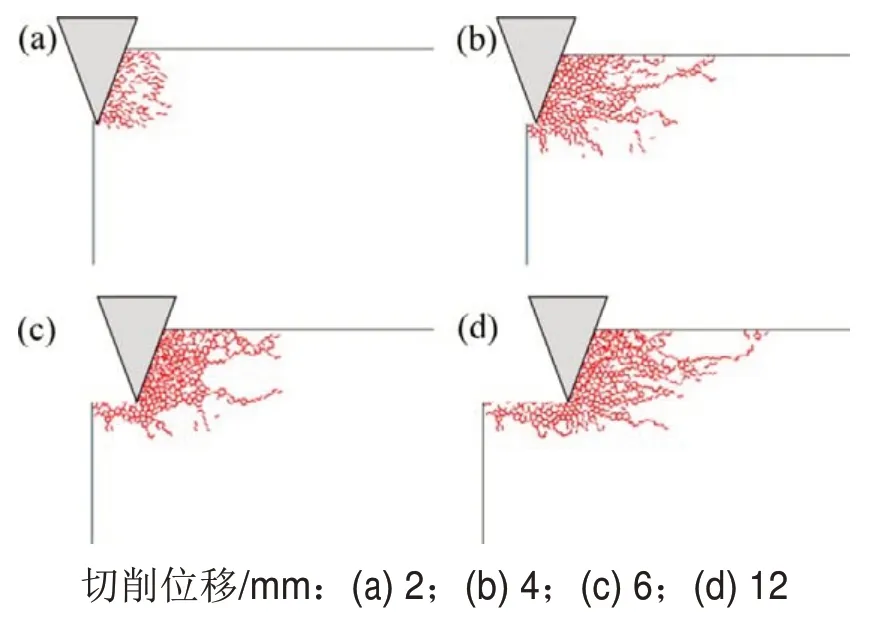
图9 不同切削位移下裂纹扩展规律Fig.9 Crack propagation law under different cutting displacements

钻刃在切削煤体的过程中，因钻刃推进速度不变、煤体本身性质不变以及煤体的破坏形式不变，因此，在不同煤体应力下，整个切削过程中产生的裂纹总数量差异不大。为了分析煤体应力对裂纹发展的影响规律，取切削过程的1个完整周期，分析不同煤体应力下裂纹数量与切削时步的关系，如图10所示。由图10可见：不同煤体应力下裂纹数量变化呈现相似的规律，即随着钻刃的推进，裂纹数快速增大，当产生主裂纹后，裂纹数量增加明显变缓；出现主裂纹时，裂纹总数与煤体应力关系不大，但在裂纹数量缓慢增加，煤体应力小的情况下，裂纹数量较多。

图10 裂纹数与时步变换的关系Fig.10 Relationship between the number of cracks and time-step transformation

3.3 煤体应力对切削力的影响规律

井下的应力范围一般为15～30 MPa，为分析煤体应力对钻头转动切削力的影响规律，对试件施加不同煤体应力，根据PFC 模拟结果得到不同煤体应力下切削力与切削位移的关系，如图11所示。

由图11可以看出：切削力随切削位移的增大呈明显周期变化，变化规律与实际切削实验结果一致；当煤体应力为10 MPa 时，切削力峰值为120 kN，理论值为96 kN，后者与前者的比值为0.8；当煤体应力为15 MPa 时，切削力峰值为158 kN，理论值为117 kN，后者与前者的比值约为0.74；当煤体应力为20 MPa 时，切削力峰值为191 kN，理论值为144 kN，后者与前者的比值约为0.75；当煤体应力为25 MPa 时，切削力峰值为223 kN，理论值为179 kN；当煤体应力为30 MPa时，切削力峰值为258 kN，理论值为212 kN。综上可知，切削力的峰值、平均值与煤体应力呈线性关系，切削力理论分析结果与数值模拟峰值的比值近似为0.76，存在一定误差，这是因为理论分析中忽略了钻刃与煤壁的摩擦力。

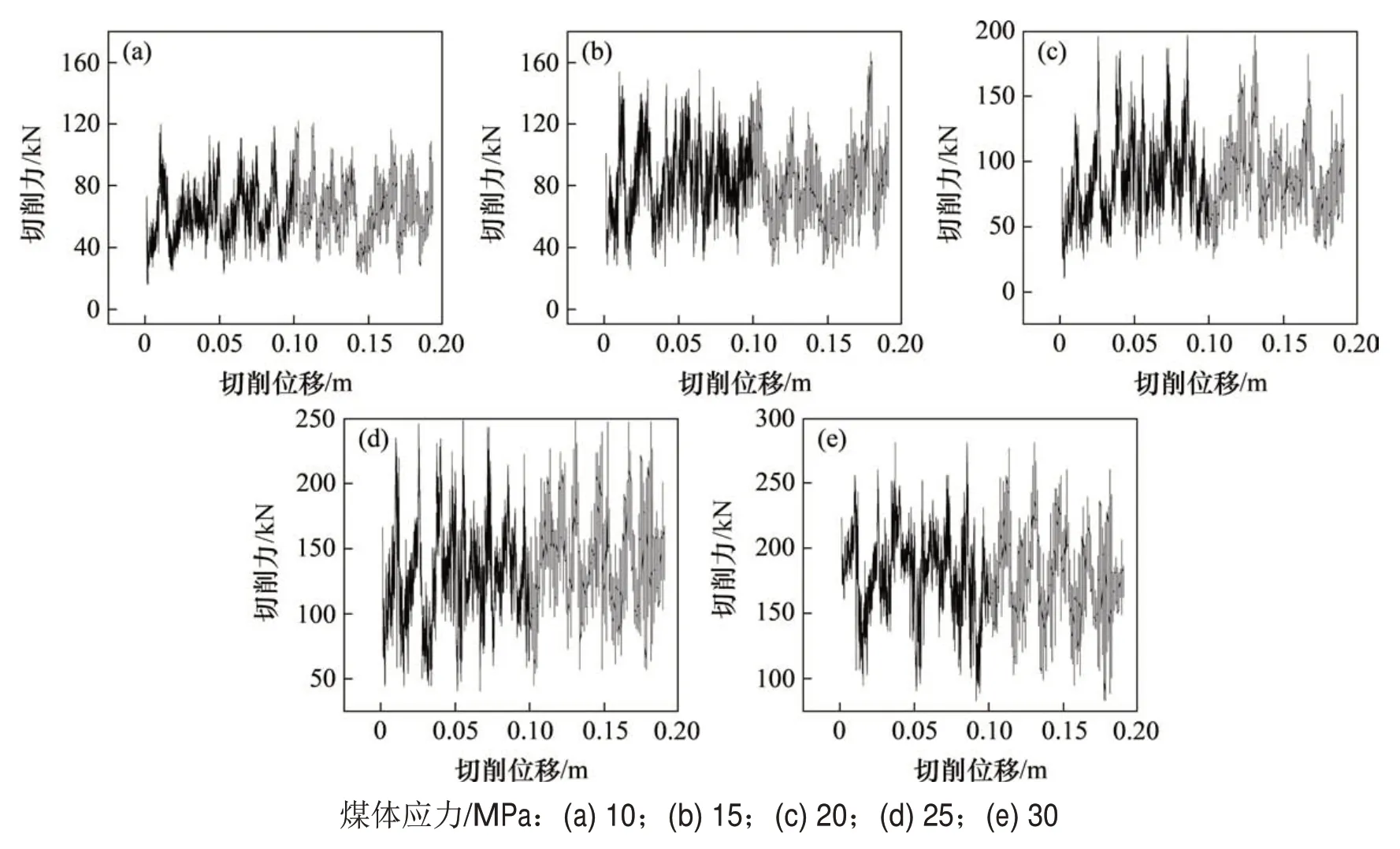
图11 切削力随切削位移的变化Fig.11 Variation of cutting force with cutting displacement

图12所示为模拟切削力峰值、平均值、理论值与煤体应力的关系曲线，可见3 条直线几乎平行。考虑到理论模型中略去了钻刃底部与煤体的摩擦力，因此，在相同煤体应力下，模拟切削力峰值比理论值大。

图12 切削力随煤体应力的变化Fig.12 Variation of cutting force with coal body stress

4 结论

1)切削力主要受煤体应力、切削深度、钻刃半角等因素影响。在煤岩物理力学条件不变时，切削力与煤体应力呈线性关系，可以根据切削力的变化反演钻孔过程中的煤体应力分布，这为煤体应力原位探测提供了新思路。

2)切削力与钻刃半角有关，当钻刃半角较小时，对切削力影响较小；当钻刃半角增大到20°时，切削力快速上升，存在最佳钻刃半角，为20°左右，既能保证切削力较小，又能减小钻刃磨损。

3)在切削过程中，随着煤体应力的增大，出现主裂纹时裂纹总数与煤体应力关系不大，但在裂纹数量缓慢增加，煤体应力较小的情况下，裂纹数量较多。

4)切削力随切削位移的增大呈明显周期变化，与切削实验结果一致，切削力的峰值和平均值均与煤体应力呈线性关系，切削力理论分析结果与数值模拟峰值的比值近似为0.76。