一种基于PSO-CSP-SVM的运动想象脑电信号特征提取及分类算法
刘宝,蔡梦迪,2,薄迎春,张欣
(1.中国石油大学(华东)控制科学与工程学院,山东青岛,266580;2.浙江大华技术股份有限公司,浙江杭州,310053)
脑机接口(brain computer interface,BCI)技术可以不依赖外周神经和肌肉组织组成的正常大脑信息输出通道,直接实现人脑与计算机或其他电子设备之间的信息交流和通信控制[1],因此,脑机接口技术可以为大脑功能正常,而中枢神经或运动系统受到严重损伤的患者提供一种辅助康复和生活自理的方式[2]。此外,脑机接口技术在交通控制、军事、娱乐等领域也得到广泛应用。基于运动想象脑电信号的BCI技术是目前BCI技术的主要研究方向之一,其关键技术在于脑电信号特征的有效提取和准确分类。研究表明,人在进行某个肢体运动或想象肢体运动时会出现事件相关去同步现象(event-related de-synchronization,ERD)和事件相关同步(event-related synchronization, ERS)现象[3],这2 种生理现象成为研究脑电信号分类的理论基础。与ERD/ERS 现象相关的常用特征提取算法有功率谱分析法、小波变换和共空间模式(common spatial patterns,CSP)等[4-8],其中CSP算法被广泛地应用于运动想象脑电信号的模式分类中,是最有效的脑电信号特征提取方法之一。常用的分类算法有线性判别分析、人工神经网络、贝叶斯分类器和支持向量机(support vector machines,SVM)等,其中SVM在处理小样本、高维度、非线性问题时具有明显的优势,且具有较强的泛化能力和鲁棒性,被广泛应用于分类问题中。由于脑电信号具有个体差异性问题,不同受试者与运动想象相关的ERD/ERS 现象往往出现在不同的频率范围和时间段内。目前大多数研究学者为解决个体差异性问题,一般都是对脑电信号的频段和时间段进行人工选择。例如ANG等[9-10]提出的滤波器组共空间模式算法和判别式滤波器组共空间模式算法都是将频段划分为不同的子频带,依据不同的标准选择出最佳频带,而没有对脑电信号的时间段进行优化;马满振等[11]设置时长分别为1,2,和3 s 的固定时间窗,以选择最优时间段,但没有考虑频率因素;韩仁香[12]利用滑动窗采用循环方式,不断改变时间窗的时长、时间起点和频率带宽、频率初始点来确定最佳时间段和频段,但其研究中,频率子带和时间子带的带宽往往是常量,且这2个因素的优化过程是独立进行的,对频段和时间段之间的相关性考虑不足,导致难以获得精准的最佳频段和时间段。针对脑电信号存在个体差异性导致多类运动想象脑电信号特征提取不准确,从而影响分类准确率的问题,本文作者提出一种基于PSO-CSP-SVM 的运动想象脑电信号特征提取及分类算法。该算法首先利用PSO 准确优化出不同个体脑电信号的最佳时频参数,同时获得与运动想象相关性最大的脑电信号时间段和频段;然后,利用“一对多”CSP(one versus rest CSP, OVR-CSP)对基于优化时频段的脑电信号进行特征提取;最后,利用“一对一”SVM(one versus one SVM,OVO-SVM)对脑电特征进行分类识别,并且将分类错误率作为PSO 算法的适应度函数值。选择BCI2005desc_Ⅲa数据集以验证所提算法的有效性和分类效果。
1 运动想象脑电信号(EEG)生理机制
1.1 EEG的产生机制
人脑是中枢神经系统的重要组成部分,主要包括大脑、小脑、脑干和间脑4个部分[13]。大脑的表层部分是大脑皮层,大脑皮层上的神经元是人脑中处理信息的基本单元,主要由细胞体、树突和轴突组成。神经元活动时,神经递质在神经元之间传递形成微弱的电流,当足够多的神经元活动模式相同时,才能通过脑电仪器检测到大脑皮层的脑电信号。目前公认脑电信号的主要成分是大脑皮层内神经细胞群同步活动时突触后电位的总和[13]。
1.2 EEG的采集
目前EEG 的采集主要使用非植入式方法,非植入式采集方式将电极帽放置在头皮表面。电极位置的分布普遍依据国际脑电图学会制定的“10-20国际标准导联系统”,该系统的定位标准为:将从鼻根到枕骨粗隆的连线10 等分,从鼻根开始,间距为10%,20%,20%,20%,20%和10%的位置依次为Fpz,Fz,Cz,Pz,Oz 和枕骨粗隆;将左右耳廓最高点的连线10 等分,从左耳开始,间距为10%,20%,20%,20%,20%和10%的位置依次为T3,C3,Cz,C4,T4和右耳垂[14]。具体电极分布如图1所示。目前常用的64导、128导电极帽也是从10-20标准导联系统扩展而来。
1.3 EEG进行分类的生理基础
现代神经电生理学研究表明:当人类在进行实际肢体运动或者进行运动想象时,大脑皮层的某个区域会被激活,该区域代谢速度加快,血流量增加,使脑电信号相应频段的幅值降低,发生频带能量降低,该生理现象称为ERD;相反,ERS 指大脑某个区域处于静息或惰性状态时,脑电信号出现的频带能量升高的现象[3]。当大脑进行不同类别的运动想象时,ERD/ERS 现象会出现在大脑皮层的不同区域,具有空间特性。例如进行左手运动想象时,大脑右半球C4 区域产生的脑电波幅值降低,出现ERD 现象;同时,大脑左半球C3 区域产生的脑电波幅值增加,出现ERS 现象。进行右手运动想象时的ERD/ERS 现象分布与左手运动想象的情况正好相反,即大脑左半球C3 区域出现ERD 现象,而右半球C4 区域出现ERS 现象。此外,ERD/ERS 现象还具有频段特性。ERD/ERS现象主要出现在频率范围为8~12 Hz的mu节律和频率范围为18~26 Hz的beta节律。但是不同类别运动想象脑电信号的ERD/ERS 现象会出现在不同的频段,例如想象手运动时的ERD 现象主要出现在10~12 Hz 和20~24 Hz,想象脚运动时的ERD现象经常出现在7~8 Hz 和20~24 Hz,想象舌运动时的ERS 现象主要出现在10~11 Hz[15]。因此,ERD/ERS 现象的空间特性和频段特性为多类运动想象的分类提供了理论依据。
2 基于PSO的改进CSP运动想象脑电信号特征提取与分类方法

图1 10-20标准电极导联定位分布图Fig.1 Schematic diagram of 10-20 standard electrode lead positioning method
为解决脑电信号的个体差异性问题,以获得区分度较大的脑电特征且提高分类准确率,本文作者提出一种基于PSO-CSP-SVM 的运动想象脑电信号特征提取及分类算法。该算法主要包括PSO 算法对脑电信号时频参数的优化,OVR-CSP算法对优化时频段脑电信号的特征提取和OVOSVM 对优化时频段脑电信号的分类识别。该算法的整体结构框图如图2所示。
该算法各组成部分的工作过程如下。
1)脑电信号的时频参数优化。该部分利用PSO 算法优化出能准确定位最具区别度脑电特征的时频参数,从而获得不同个体脑电信号的最佳时间段和频段,对脑电数据分别进行时间段和频段滤波。
2)特征提取。该部分首先针对时频处理后的训练集脑电数据,采用OVR-CSP算法构建空间滤波器,然后将空间滤波器分别对训练集和测试集进行特征提取。
3)特征分类。该部分首先利用训练集脑电特征对SVM 分类器进行训练,且利用网格搜索法来优化分类器参数以提高分类器性能;然后,将训练好的SVM 对测试集脑电特征进行分类,得到最后的分类准确率,并将分类错误率作为PSO 算法评估粒子位置优劣的适应度函数值。
2.1 基于PSO的运动想象EEG信号时频参数优化
由于脑电信号具有个体差异性,不同个体在进行运动想象时,产生的最明显脑电特征会出现在不同的频段和时间段。利用先验知识对脑电数据的频段和时间段进行选择往往是不精确的;而PSO 算法具有较强的搜寻全局最优解能力,且调整参数少,收敛速度快[16],可以为不同个体优化出能准确定位最明显特征的时频参数,获得具有最佳时间段和频段的脑电信号,从而有利于后续的脑电特征提取及分类。
利用PSO 算法对脑电信号的时频参数进行优化时,假设PSO 算法中1 个粒子种群包含M个粒子,定义每个粒子的维度为4,用位置向量X来表示每个粒子个体的移动方向,用速度向量V来表示其移动的速度。那么,在四维搜索空间中,第i个粒子在第k次迭代时,其位置向量可以表示为该四维参数分别被定义为脑电信号的开始频率fstart、频率宽度fwidth、开始时间tstart和时间宽度twidth。其速度向量可以表示为定义第k次迭代时,粒子i搜索到的最优位置为Pbest,i(k),也称为局部最优位置。将该粒子的局部最优位置与粒子群中的其他粒子的局部最优位置相比较,基于最小化原则,找到最优的局部最优位置当作整个粒子群的当前全局最优位置,记为Gbest(k)。粒子群中的每个粒子根据当前的局部最优位置和全局最优位置来更新自己的速度和位置:

式中:k=1,2,…,K,为算法迭代的次数;i=1,2,…,M,为第i个粒子个体;j=1,2,3,4,为待优化问题的维度;c1和c2为加速因子,通常在[0,2]范围内取值;r1和r2为符合均分布的随机数且r1,r2∈[0,1]。用来评估局部最优位置和全局最优位置的粒子适应度F表示为

式中:a为由SVM 分类器正确识别出的测试集样本数;A为测试集样本总数。

图2 PSO-CSP-SVM算法的整体结构框图Fig.2 Overall structure diagram of PSO-CSP-SVM algorithm
经过PSO 算法的不断迭代优化,最终可以得到脑电信号开始频率fstart、频率宽度fwidth、开始时间tstart和时间宽度twidth的最优值,从而获得运动想象脑电信号的最优频段和时间段分别为[fstart,fstart+fwidth]和[tstart,tstart+twidth],为后续利用OVR-CSP 算法进行特征提取奠定基础。
2.2 基于CSP的运动想象EEG信号特征提取
运动想象脑电信号的特征提取可以从原始多维的脑电数据中提取到有效的特征,直接决定后续特征识别的正确率,对于BCI系统来说具有重要意义。CSP算法是最有效的脑电信号特征提取算法之一[17-18],针对多类运动想象脑电信号的分类,本文采用OVR-CSP算法进行特征提取。
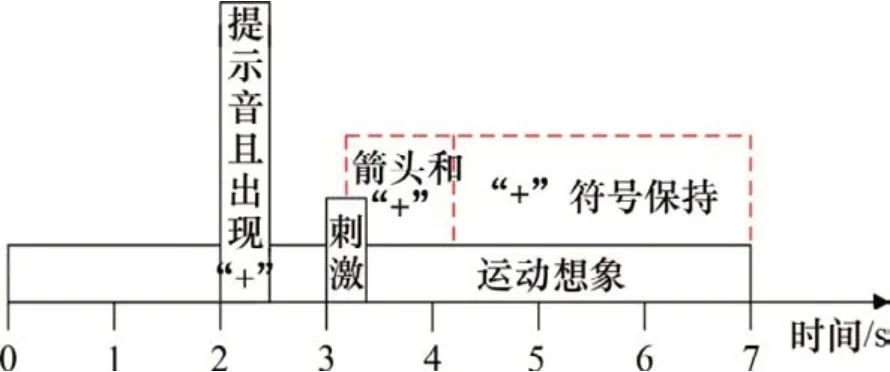
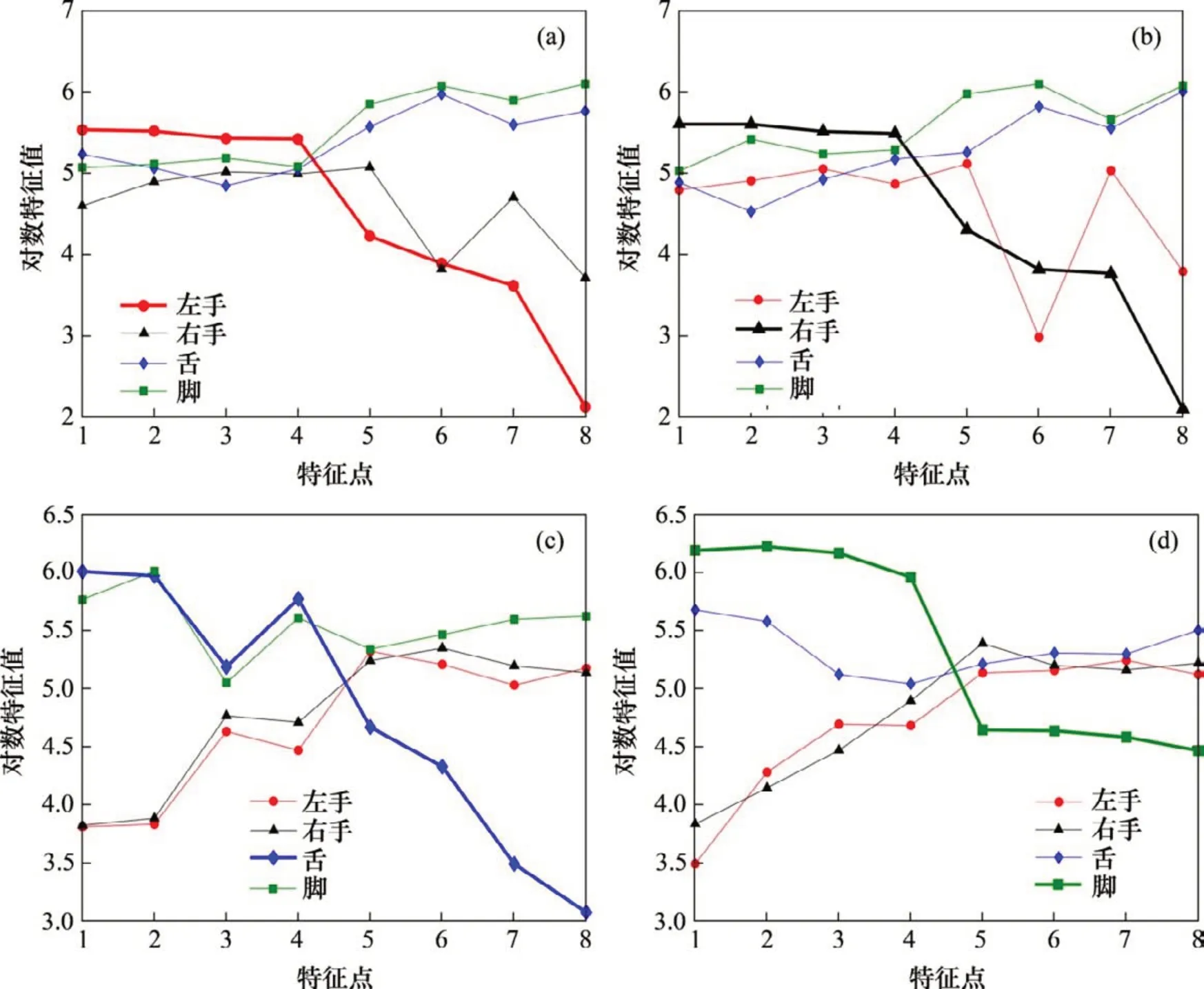
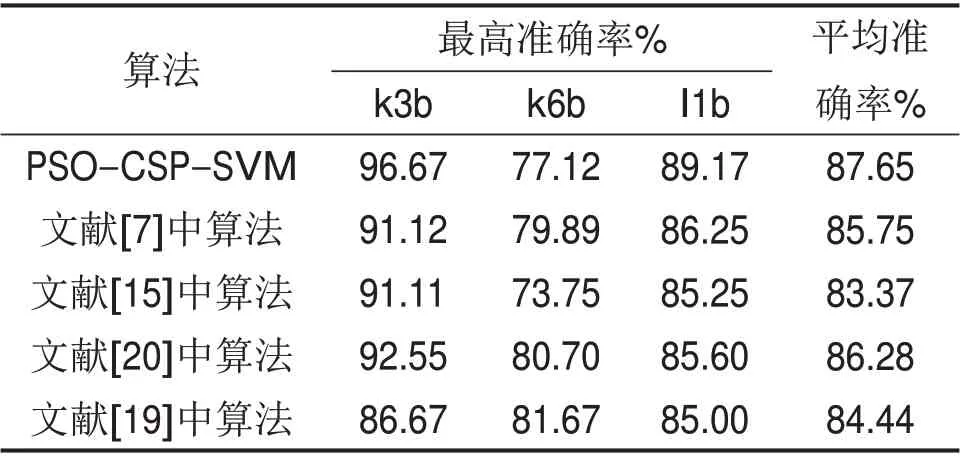
假设多类想象任务的原始脑电数据矩阵分别为Y1,Y2,…,Yn,n为任务总类别数。矩阵的维度均为N×T,其中N为通道数,T为单次试验每个通道采样点数,且N 训练集每类运动想象脑电信号Yl(l=1,2,…,n)的归一化协方差矩阵表达式如下: 式中:表示对Yl的转置,trace( )为矩阵的迹。对每次运动想象脑电数据分别求协方差矩阵,并将同一类任务下的协方差矩阵求平均值,得到平均协方差矩阵 式中:U为特征向量矩阵;λ为特征值构成的对角阵。将特征值进行降序排列,则白化矩阵为 然后对S1和S2进行主分量分解,得到: 式中:B为特征矩阵;I为单位矩阵。若将λ1中的特征值按照降序排列,则λ2中的特征值按升序排列。由于2类矩阵的特征值之和恒为1,则S1最大特征值所对应的特征向量使S2有最小特征值,反之亦然。构建投影矩阵W: 为使变换后的2类信号差异性最大化,取投影矩阵W的前m行和后m(2m≤N)行组成空间滤波器W1。将训练集和测试集的脑电信号Y分别经空间滤波器滤波后得到特征矩阵Z: Z的每个行向量对应1个通道的特征,特征值fd定义方式为 为解决脑电信号个体差异性大,受试者部分脑电特征波动剧烈的问题,对特征值取对数运算: 最后,在OVR-CSP 算法构建的n个空间滤波器滤波下,训练集和测试集里每个样本的脑电数据矩阵都可提取出为2m×n的一维特征。 在获得运动想象脑电信号较明显的特征后,可以依据样本的特征分布趋势判断运动想象任务的类别,但当脑电信号的噪声较大时则无法进行有效的识别。因此,为提高分类准确率,需要利用分类器对特征进行学习和识别,分类器的性能直接影响脑电信号最终的分类准确率。SVM 是一种具有统计学理论基础的分类算法,并且通过引入核技巧,使其成为实质上的非线性分类器。本文采用OVO-SVM 算法作为多类运动想象脑电信号的分类算法。 OVO-SVM 算法在处理多类运动想象脑电信号的分类时,需要依次利用任意2类样本构建不同的SVM 分类器。当总类别数为n时,则需要构建n(n-1)/2 个SVM 分类器。对于包括左手、右手和舌等在内的多类脑电信号,可以先构建左、右手运动想象脑电信号之间的SVML,R分类器,然后依次构建其他类信号之间的多个分类器。其中,构建左、右手运动想象脑电信号之间的分类器过程如下。 假定运动想象脑电信号的训练数据集D为 式中:tp(p=1,2,…,P)为第p个特征向量;sp为tp的类标签,且sp∈{+1,-1}。将左手视为正类,标签为+1,右手视为负类,标签为-1。SVM 的目标就是寻找1个最优超平面,以使每一类数据支持向量之间的分类间隔达到最大。分离超平面定义为w*·t+b*=0,由法向量w*和截距b*决定。 对于解决运动想象脑电信号线性不可分问题,SVM 寻找最优超平面的过程就是求解如下的凸二次规划问题: 式中:C为惩罚参数且C> 0;ξp为松弛变量。通过Lagrange乘子法可得到: 式中:αp(p=1,2,…,P)和αq(q=1,2,…,Q)为拉格朗日向量;sq为tq的类标签。 对式(17)求解得: 因此,可以得到分类超平面和决策函数表达式: 此时,SVM 也会通过引入核函数的方法来解决脑电信号的线性不可分问题,用H(tp,tq)代替式(17)中的内积tp·tq。将原空间的特征向量映射到高维空间,使其实现线性可分。由于脑电信号是非线性的,本文核函数则选用径向基函数,其表达式为 其中:g为高斯核的带宽且g> 0。此情形下分类决策函数表达式为 惩罚参数C和核函数参数g是影响SVM 分类效果的主要因素,本文选用网格搜索法进行这2个参数的寻优。 然后,OVO-SVM 算法依次利用训练集中任意2类样本构建SVM分类器,最终得到n(n-1)/2个SVM分类器。 在测试新样本时,将新样本的特征依次输入这些分类器,然后采取投票机制。若每个分类器的判定结果属于第1 类,则第1 类的票数加1,否则第2 类加1。例如当左、右手之间的分类器SVML,R的判定结果为左手时,左手的票数加1,否则右手加1;当左手和舌之间的分类器SVML,T的判定结果为左手时,左手的票数加1,否则舌的票数加1。最终依据n(n-1)/2 个分类器的判定结果将票数最高的类别作为测试样本的输出类别。 综上可知,基于PSO-CSP-SVM 的运动想象脑电信号特征提取及分类算法整体流程图如图3所示。 从图3可以看出PSO-CSP-SVM算法的具体步骤如下: 1)随机初始化粒子种群中M个粒子的位置x和速度v; 2)利用每个粒子当前位置的四维参数值分别对训练集和测试集的原始运动想象脑电数据进行时频处理; 3)利用OVR-CSP算法对处理后的脑电数据进行特征提取; 4)利用OVO-SVM 算法对训练集提取出的脑电特征进行训练后,对测试集的脑电特征进行测试,得出分类准确率; 5)计算每个粒子的适应度; 6)由适应度评估出每个粒子的局部最优位置Pbest及粒子群的全局最优位置Gbest; 7)利用公式(1)和(2)更新每个粒子的速度和位置; 8)重复步骤2)~7),直到满足分类准确率要求或达到最大的迭代次数。 图3 PSO-CSP-SVM算法的整体流程图Fig.3 Overall flow chart of PSO-CSP-SVM algorithm 基于PSO-CSP-SVM 的运动想象脑电信号特征提取及分类算法的实验仿真条件为:CPU,Intel(R) Core(TM) i5-5200U(2.20GHz);RAM, 8.0 GB,Windows 10,MATLABR2017b。本文采用BCI2005desc_Ⅲa数据集,该数据集包括k3b,k6b和l1b33名受试者的4类运动想象(左手、右手、舌和脚)脑电信号。数据用64 导Neuroscan 脑电放大器采集获得,采样频率为250 Hz,并对数据进行了1~50 Hz的滤波处理。实验过程如图4所示。从图4可见:前2 s,受试者处于安静状态;在第2 s时,计算机发出提示音且屏幕上出现“+”,提示受试者运动想象即将开始;自第3 s 开始,计算机屏幕出现向左、向右、向上或向下的箭头1 s,要求受试者根据箭头方向分别进行左手、右手、舌和脚的运动想象,一直到第7 s 结束[19]。其中受试者k3b的4类运动想象各采集90组,共360组;受试者k6b和l1b的4类运动想象各采集60组,共240组。将每名受试者运动想象样本集的一半作为训练集,另一半作为测试集。 图4 实验过程时序图Fig.4 Timing chart of the experimental process 为了分析在进行运动想象任务时出现的ERD/ERS 特征,本文采用功率谱分析法对脑电信号进行处理。功率谱分析法可以将幅值随时间变化的脑电数据变为脑电功率随频率变化,从而可检测到不同运动想象任务引发的不同ERD/ERS 现象。以k3b受试者的左、右手运动想象数据为例,分析其出现ERD/ERS 现象的空间特性和频段特性,其左、右手运动想象与休息状态时的脑电数据在导联C3 和C4 上的功率谱密度图如图5所示。从图5可以看出:在进行左、右手运动想象任务时,在脑区对侧会出现ERD 现象,而在脑区同侧出现ERS 现象;即在进行左手运动想象时,对大脑右半球C4导联的功率谱分析反映出ERD现象,对大脑左半球C3 导联的功率谱分析反映出ERS 现象。但是进行右手运动想象时出现的ERD/ERS 现象分布导联正好与左手运动想象时的相反。由图5还可见:在进行左、右手想象运动时,ERD/ERS 现象主要出现在了10~12 Hz和20~24 Hz频段。因此,基于ERD/ERS 现象的空间和频段分布特性,针对包含左手、右手、舌和双脚4类运动想象脑电信号的BCI2005desc_Ⅲa数据集,可以通过采用有效的特征提取和分类算法,获得与运动想象相关的脑电特征,从而准确识别出4类脑电信号。 利用PSO算法对BCI2005desc_Ⅲa数据集的脑电信号进行时频参数优化时,由于进行运动想象的时间段是3~7 s,脑电信号的采样频率为250 Hz,则有效时间段上的脑电数据采样点范围为[750,1 750]个,且与运动想象相关的ERD/ERS现象主要出现在8~30 Hz。因此,对PSO 算法中每个粒子四维位置参数fstart,fwidth,tstart和twidth搜索范围的设置方式如表1所示,且当tstart和twidth对应的采样点数之和(Mtstart+Mtwidth)大于1 750个时,Mtwidth=7×250-Mtstart;当fstart+fwidth> 30 Hz 时,fwidth=30-fstart。 图5 左右手运动想象与休息状态在C3和C4导联上的功率谱密度图Fig.5 Power spectral density plots of left and right hand motion imagination and rest on C3 and C4 lead 表1 PSO算法粒子位置参数的搜索空间Table 1 Search space of PSO algorithm particle position parameter 在实验仿真中,将PSO 算法的迭代次数设置为10,粒子个数M的取值为15。k3b,l1b 和k6b这3名受试者脑电数据在迭代优化过程中的适应度曲线如图6所示,最终3名受试者经PSO算法优化得到的脑电信号最佳时频参数如表2所示。实验结果表明,PSO 算法能够有效优化出不同个体脑电信号的最佳时频参数。 图6 3名受试者的PSO算法适应度曲线Fig.6 PSO algorithm fitness curve of three subjects 表2 3名受试者的最佳时频参数Table 2 The best time-frequency parameters of the three subjects 在4 类运动想象(左手、右手、舌和脚)任务分类中,OVR-CSP 算法需要构建4 个空间滤波器,即W1,W2,W3和W4。将特征点对数m的取值设置为4,即每个滤波器由投影矩阵的前4 行和后4 行组成。那么,单次实验样本可以由4个空间滤波器得到1×32 一维特征向量。其中受试者k3b 训练集的各类运动想象任务在4个空间滤波器作用下提取的特征值如表3所示,特征分布趋势如图7所示。由图7可以看出:每一类运动想象在对应自己滤波器下的特征分布基本呈下降趋势,与其他3类相比具有较明显的区别。因此,OVR-CSP算法可以有效地提取4类运动想象脑电特征,有利于进行后续的分类识别工作。 采用OVO-SVM算法进行4类运动想象脑电信号分类时,需要构建6组分类器。由网格搜索法得到分类器惩罚参数C和核函数参数g的最优值以及交叉验证准确率(cross validation accuracy,CVA,变量用PCVA表示),3名受试者各自的分类器参数最优值及PCVA如表4所示。 对每名受试者单次运动想象任务脑电信号都选取3~7 s的固定时间段和8~30 Hz的固定频段,然后同样采用OVR-CSP 算法进行特征提取及OVO-SVM 算法进行分类,将其得到的分类结果与本文基于优化时频段得到的结果进行对比,如表5所示。 从表5可以看出:针对优化时频段脑电信号时,SVM 分类器对受试者k3b,k6b 和l1b 的最终准确率分别为96.67%,77.12%和89.17%。相比基于固定时频段的分类准率分别提高了3.34%,0.46%和6.09%,平均分类准确率提高了3.29%,证明了本文所提算法对优化时频段的脑电信号进行特征提取及分类的有效性。 表3 受试者k3b的4类运动想象在不同空间滤波器下的对数特征值Table 3 Eigenvalues of k3b four types of motor imagery under different spatial filters 图7 受试者k3b的4类运动想象EEG特征分布Fig.7 EEG feature distribution of four types of motor imagery of subject k3b 表4 SVM分类器参数C和g的最优值及交叉验证准确率Table 4 The optimal values of SVM classifier parameters C and g and PCVA 表5 基于优化时频段和固定时频段的分类结果对比Table 5 Comparison of classification results based on optimized and specific time-frequency bands 将本文算法的分类结果与其他文献中算法的分类结果进行对比,如表6所示。其中文献[7]利用小波包分析方法进行特征提取和基于聚类思想的二叉树支持向量机进行特征识别;文献[15]采用PW-CSP 和Hilbert 变换提取特征,对SVM 进行分类;文献[20]提出二级CSP算法进行特征提取,利用SVM 得到分类结果;BCI 竞赛第1 名是利用OVR-CSP算法和SVM算法进行脑电识别[19]。从表6可以看出:对于受试者k3b和l1b的分类结果,本文所提算法的分类准确率高于文献[7,15,20]以及BCI 竞赛第1 名所采用算法[19]的分类准确率,最高分类准确率为96.67%;对于受试者k6b 的分类结果,本文算法所得分类准确率略低于其他算法的分类准确率。从3 名受试者的平均分类准确率来看,本文所提算法明显优于其他文献中的算法,平均分类准确率达到87.65%,为多类运动想象脑电信号分类问题的研究提供了新思路。 表6 与其他文献的分类结果对比Table 6 Comparison of classification results with other literatures 1)为解决个体差异性导致的多类脑电信号特征提取困难和分类准确率较低的问题,提出一种基于PSO-CSP-SVM 的运动想象脑电信号特征提取及分类算法。 2)该算法包括利用PSO 算法对脑电信号进行时频参数优化、基于优化时频段脑电信号利用OVR-CSP算进行特征提取和OVO-SVM算法进行特征分类3个部分。将该算法应用于BCI2005desc_Ⅲa数据集,可对4类运动想象脑电信号进行分类,同时该算法也适用于其他脑电信号数据集。 3)与其他算法的分类结果进行对比,本文提出的算法提高了运动想象脑电信号的平均分类准确率,且最高分类准确率可达96.67%。证明了本文算法的有效性,可为BCI系统研究提供参考。








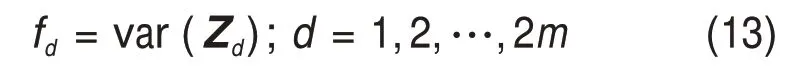

2.3 基于SVM的运动想象EEG信号分类


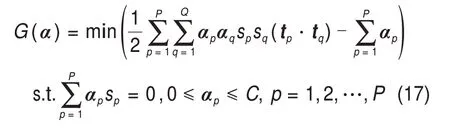
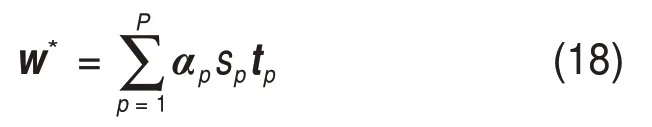
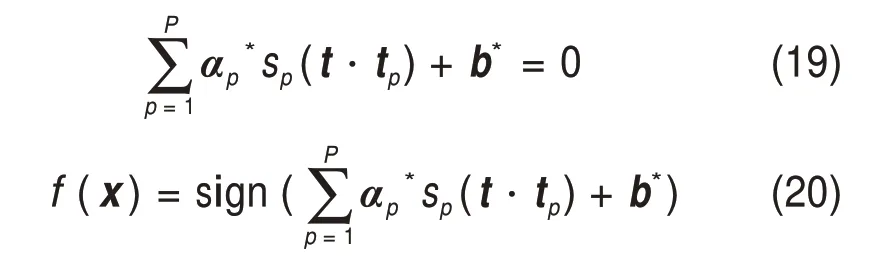

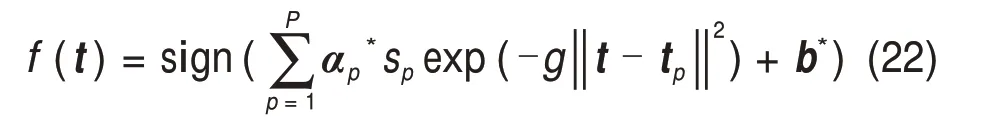

3 实验结果分析
3.1 实验条件与数据来源
3.2 4类运动想象EEG信号时频参数优化结果




3.3 4类运动想象EEG信号特征提取分析
3.4 4类运动想象EEG信号分类结果及对比分析



4 结论

