TBM盘形滚刀切削力学模型分析

张桂菊，谭青，劳同炳

(1.高效动力系统智能制造湖南省重点实验室，湖南邵阳，422004；2.中南大学机电工程学院，湖南长沙，410083；3.邵阳学院机械与能源工程学院，湖南邵阳，422004)

岩石掘进机(tunnel boring machine，TBM)是地下空间隧道掘进的主要工具，在其施工过程中，作为掘进机主要的刀具之一的盘形滚刀，直接参与掘进破岩的工作[1-2]。对盘形滚刀与岩石的作用机理进行研究，分析刀具的载荷规律，建立刀具破岩的力学模型，有利于研究分析刀盘推力、刀盘扭矩以及掘进机的掘进性能，对于提高破岩掘进效率意义重大[3-7]。对于硬岩掘进机的盘形滚刀破岩机理，国内外学者进行了大量的研究[8]。EVANS等[9]对盘形滚刀破岩过程进行了研究，认为岩石属于挤压破坏，在破岩过程中，滚刀的垂直推力与其滚压的岩石范围投影于岩石的面积呈正比。AKIYAMA[10]利用剪切破碎理论和挤压破碎理论，对TBM 盘形滚刀破岩时的受力分布进行了分析。NISHIMATSU[11]认为岩石破坏面属于剪切破坏，岩石被破碎并压实而形成密实核，并根据摩尔强度理论，得出了岩石剪切破坏的刀具切削力表达式。谭青等[12]利用有限元软件建模分析得到滚刀切割岩石过程受到的三向力。屠昌峰[13]在接触应力模型的基础上建立了盘形滚刀侧向力预测模型。WANG 等[14]准确预测了其复合地层土压平衡盾构机滚刀的磨损量与切削距离寿命，得到了适用于软硬不均复合地层的滚刀磨耗系数。SHI等[15]对盘形滚刀与岩石之间的接触载荷分布模型进行了分析，得出了不同贯入度下接触载荷分布曲线变化。上述研究对于理解盾构刀具破岩特性分析具有指导意义。然而，前人的研究没有从密实核角度出发，对刀具的载荷计算尚不够深入。本文作者以剪切应力强度理论为基础，分析密实核对岩体的作用，建立考虑密实核作用的摩尔-库仑强度理论滚刀刀具载荷计算模型，得出盘形滚刀侵入破岩的力学模型表达式，以期为滚刀刀具的设计研究提供参考。

1 TBM盘形滚刀切削机理

全断面岩石掘进机示意图如图1所示。掘进机中所使用的破岩滚刀主要有齿面滚刀、镶嵌硬质合金滚刀、单刃、双刃、三刃(或多刃)盘形滚刀，其中盘形滚刀是硬岩掘进机的主要破岩工具。美国罗宾斯公司最早开始使用盘形滚刀，与初期的切刀相比，盘形滚刀具有破岩效率高、刀具磨损量小、比能耗低等特点。在隧道开挖过程中，盘形滚刀由于岩石的摩擦作用在TBM 刀盘的开挖面上不断滚动，同时，在刀盘的垂直推力作用下，TBM 盘形滚刀做直线侵入运动，当滚刀作用的载荷超过岩石的强度时，岩石会发生破裂并出现剥落现象。

图1 全断面岩石掘进机Fig.1 Full-face tunnel boring machine

在刀盘上，滚刀的布置形式要以便于顺次破岩为主，也就是说，前一把滚刀接触岩石后形成较易切割的裂纹和轨迹，要为后一把滚刀破岩做好预破岩准备，使2把滚刀的裂纹能够贯通，形成破碎块岩片，达到破岩的目的。在满足顺次破岩这一点要求上，双刃和多刃滚刀不及单刃滚刀好，并且还极易造成刀刃的受力不均和不均匀磨损，从而导致刀具浪费。因此，在刀盘空间允许的情况下，布置刀具时，无论中心刀还是边刀，应尽可能选用单刃滚刀。

盘形滚刀侵入破岩时岩石的破碎体系如图2所示。通过研究滚刀侵入岩石过程发现：安装在刀盘上的盘形滚刀侵入岩石时，首先，在刀盘的推力和扭矩作用下，盘形滚刀在掌子面上形成一系列的同心圆形状的沟槽；而在岩石内部，滚刀刀刃下方则形成了高应力区，由于盘形滚刀的作用，岩石内部的微裂纹被压实，甚至闭合；当盘形滚刀侵入的总应力大于岩石强度时，岩石就发生失效，产生破坏。密实核的形成过程为：在破岩过程中，盘形滚刀不断对岩石进行剪切、挤压、拉裂等综合作用，从而导致在岩石的掌子面上不断剥离出细小的破碎颗粒；紧接着，这些细小的破碎颗粒又被连续工作的盘形滚刀碾压成细碎的粉末状，从而形成了密实核；岩石的内部能量通过密实核传递到附近区域，又会使岩石再次产生新的裂纹，按照裂纹在岩石内扩展路径的不同，又可以分为中间裂纹、侧向裂纹、径向裂纹等，其中，侧向裂纹可扩展至自由面，发展形成块岩，从而剥落；另一方面，径向裂纹和中间裂纹则会引起岩石更深部分的失效破裂[16]；当滚刀刀间距满足一定条件时，相邻滚刀之间内侧向裂纹、横向裂纹以及径向裂纹便会相互贯通，从而形成岩石碎片并剥落，至此，盘形滚刀完成了1 次破岩过程。

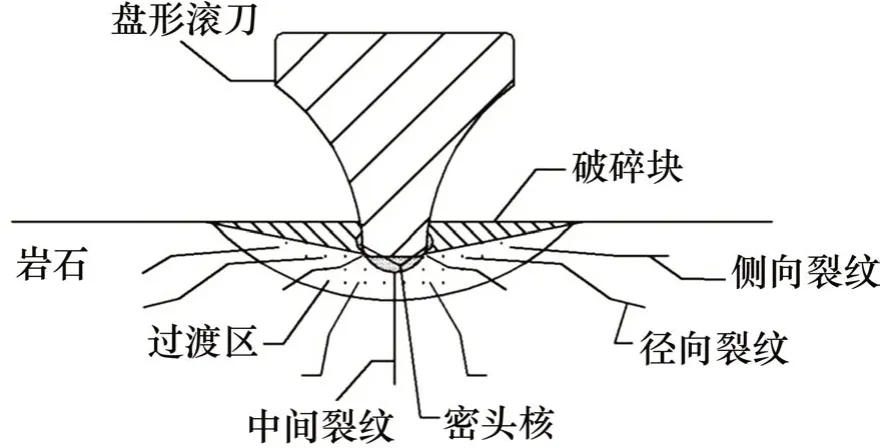
图2 滚刀作用下岩石失效示意图Fig.2 Diagram of rock failure under action of disc cutter

2 滚刀侵入破岩数学模型

建立如图3所示的微元角度为dθ的滚刀压头侵入岩石的力学模型，滚刀剖面应力分布示意图如图4所示。硬岩掘进机盘形滚刀侵入岩石过程中，滚刀与岩石相互接触的区域在较小的体积之内产生了极大的接触应力，在滚刀下方及两侧附近形成密实核，滚刀两侧上方由于过早破碎剥落，忽略其对滚刀的作用力，根据摩尔-库仑破坏准则[16]，假设岩石破碎是由剪切应力引起的，且遵守摩尔-库仑强度理论；破碎面受到压应力σ和剪切应力τ共同作用，如图3所示；同时还可看出密实核的形状由一段圆弧构成，圆弧段的圆心为O′，半径为r，圆弧最高点距离底部即密实核的长度为a。

图3 微元dθ滚刀压头破岩力学模型Fig.3 Mechanical model of micro-element dθ of disc cutter head invading into rock

图4 滚刀剖面应力分布示意图Fig.4 Diagram of stress distribution in section of disc cutter

假设微元滚刀压头侵入岩石深度为h，根据力学分析方法，滚刀在侵入时，必须要克服摩擦力dF和岩石的强度dQ。当dθ微元滚刀压头侵入岩石时，其受到的作用力dP为

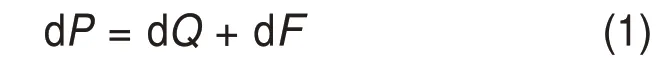
此时，岩石的强度dQ为

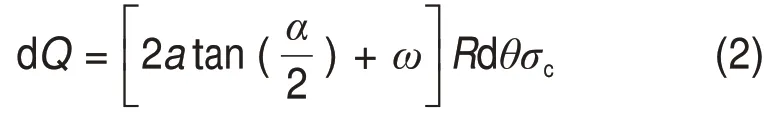
即岩石的抗破碎强度dQ为滚刀侵入刀刃在垂直方向上的投影面积与岩石抗压强度的乘积。其中，σc为岩石单轴抗压强度，α为刀刃角，R为滚刀半径，ω为刀刃宽度。

根据图3所示的几何关系可得通过密实核作用于岩石破碎块的合力F1为

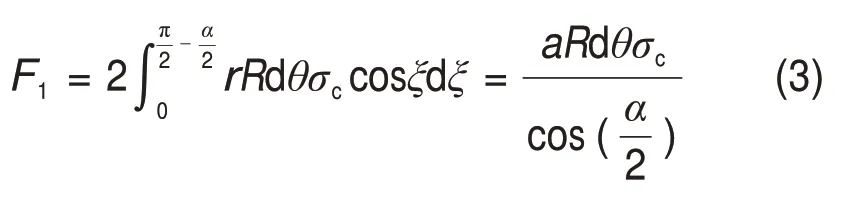
式中：ξ为滚刀与岩石接触角。

当作用力足够大时，岩块在剪切应力的作用下，以破碎角2β沿着线AB破碎，极限剪切应力满足摩尔-库仑理论。

式中：τ为剪切面上的剪应力；σ为剪切面上的正应力；φb为岩石的内摩擦角；c为岩石的内聚力。

对于破碎块进行受力平衡分析可得：

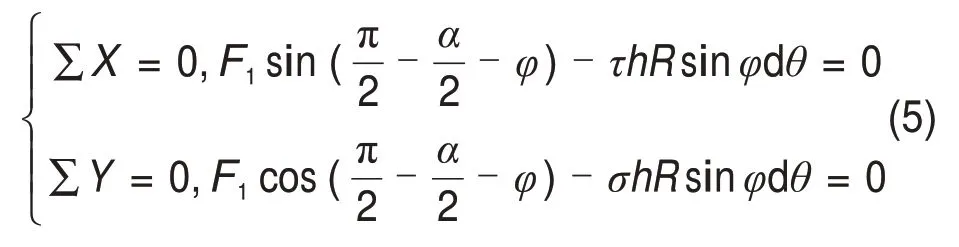
式中：∑X=0表示岩石破碎块在X方向上所受合力为0；∑Y=0 表示岩石破碎块在Y方向上所受合力为0；φ为剪切面与水平面的夹角，φ=(π-2β)/2；2β取120°～150°[17]。

将式(3)和式(4)代入式(5)可得密实核的长度a为

另外，岩石抗破碎强度dQ滚刀两侧楔形面的分量与岩石正压力dN1相平衡，即

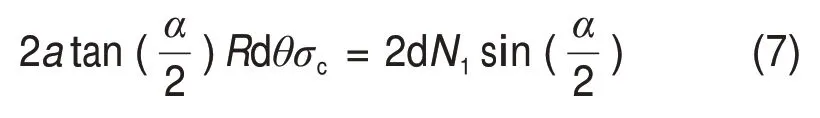
所以，刀刃侵入总摩擦力dF为

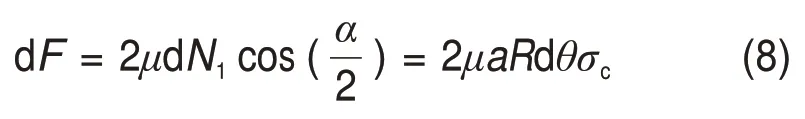
式中：μ为岩面与滚刀楔形面的摩擦因数，μ=0.40～0.55[18]。

因此，dθ微元滚刀压头侵入岩石受到作用力dP为

ROSTAMI 等[19]计算得到岩石压碎区的压力P沿着圆周方向上的分布应满足

式中：θ为某一具体圆周角(工程计算中，常常取为0～φ)；ψ为接触压力分布指数(通常取0.2～0.2)，由经验可取ψ=0.1[20]；P0为位于滚刀刀刃正下方的基准应力，取值为单位长度下的dP，即

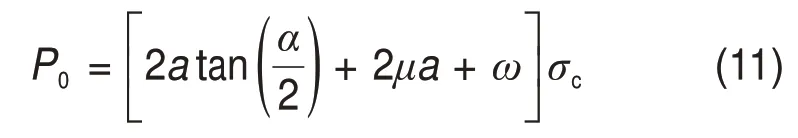
所以，滚刀接触区受到的合力F为

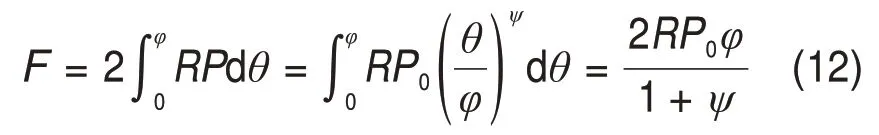
盘形滚刀侵入破岩受到的两侧侧向力大小相等，方向相反，滚动水平力为0，垂直力FV为

式中：β为垂直力和滚动力的合力与滚刀垂直方向之间的夹角，β≈φ/2。

3 滚刀侵入岩石离散元建模

3.1 岩石宏观力学参数测试

利用颗粒流离散元程序PFC2D对岩石进行数值模拟：首先应根据岩石力学性能测试的标准，分别制作直径×长度为50 mm×100 mm 和50 mm×150 mm 的2 种标准圆柱岩石试件，然后通过电液伺服控制材料试验设备对岩石试件的力学参数进行巴西劈裂和单轴压缩试验，如图5所示，可以得到岩石材料的宏观力学参数，如表1所示。

图5 岩石试样力学参数测试Fig.5 Testing of mechanical parameters for rock samples

表1 岩石试件的宏观力学参数Table 1 Macroscopical parameters of hard rocks samples

3.2 岩石细观参数标定

基于岩石试样的宏观力学试验参数对数值模型中的岩石样本进行巴西劈裂和单轴压缩的数值模拟[21]，离散元模型细观参数标定实验及应力-应变曲线分别如图6～7 所示。经过不断地调整细观参数，获得与岩石样本宏观性质一致的细观参数，如表2所示。

图6 离散元模型细观参数标定实验Fig.6 Calibration tests of mesoscopical parameters for discrete element model

3.3 滚刀数值模型的建立

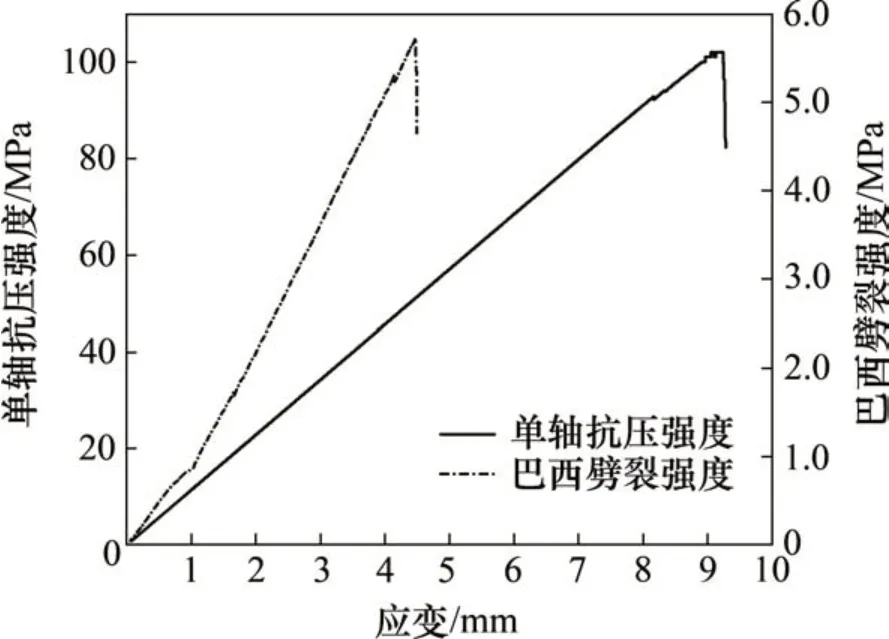
图7 离散元模型标定应力-应变曲线Fig.7 Calibration of stress-strain curve by discrete element model

表2 岩石试件的细观力学参数Table 2 Meso-mechanical parameters of hard rocks samples

根据上述标定的细观力学参数，采用空隙比生成法生成岩石试件，颗粒最小半径为0.4 mm，颗粒最大和最小半径比值为1.66，空隙率为0.08，包含颗粒数为48 694个，岩石试件宽×高为300 mm×160 mm。滚刀模型根据实验中使用的直径为432 mm的滚刀参数进行建模，先借助AUTOCAD 软件建立目标滚刀模型，再导入PFC2D中生成刚性墙体替代滚刀[22]。图8所示为滚刀破岩数值模型。

3.4 数值模拟结果

设滚刀侵入深度分别为2，4，6，8和10 mm，进行5组数值模拟分析，图9所示为不同侵入深度滚刀破岩情形。通过数值模拟之后得到滚刀侵入岩石的模拟结果如表3所示。

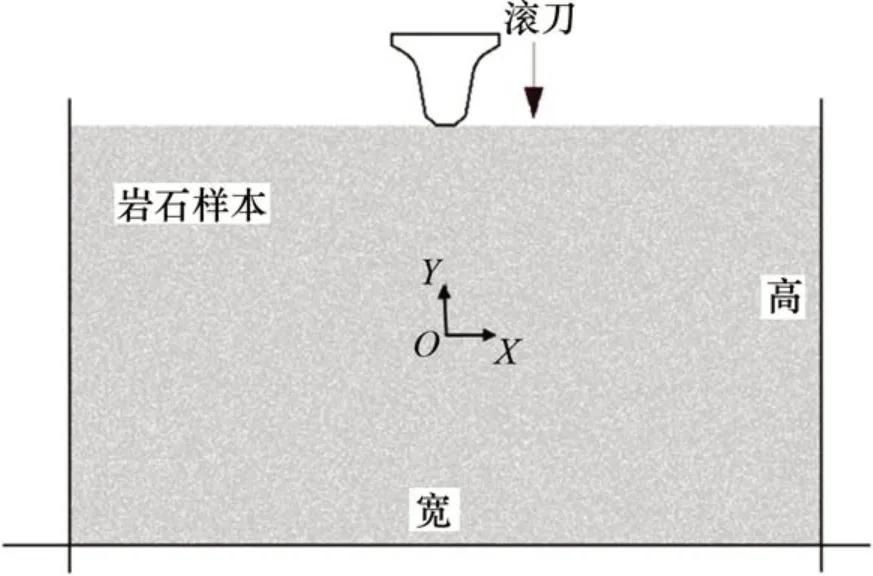
图8 盘形滚刀破岩数值模型Fig.8 Numerical model of disc cutter of breaking rock

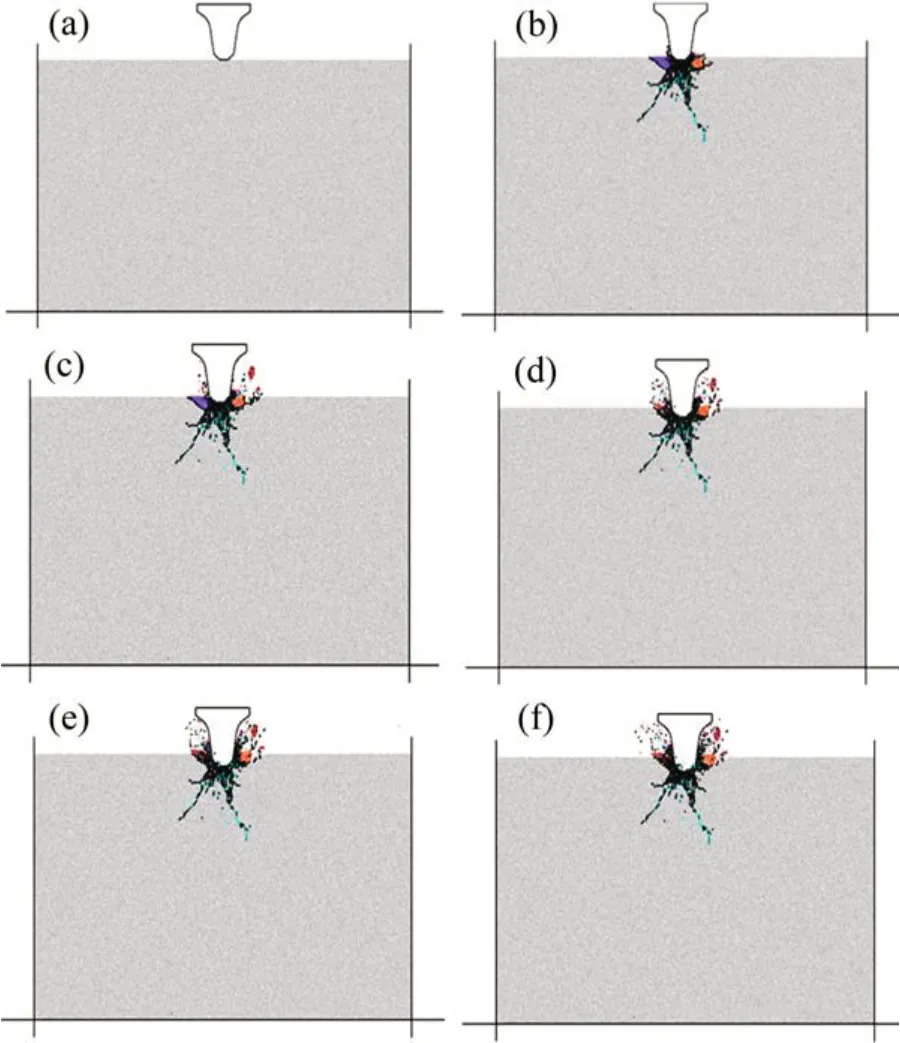
图9 不同侵入深度滚刀破岩情形Fig.9 Rock breaking shapes of different invasive depths of disc cutter

表3 垂直力数值模拟结果Table 3 Numerical simulation results of vertical force

4 盘形滚刀侵入实验

图10所示为直线式盘形滚刀破岩实验台，本文利用其对盘形滚刀破岩过程实验进行验证。实验工作台主要由机架、破岩工作台、控制台、液压系统和数据采集系统等组成。实验时，通过液压系统对实验台统进行驱动，其中垂直液压缸对盘形滚刀的上下直线运动进行驱动，另一方面，纵向液压缸对岩石的纵向进给进行驱动。

图10 直线式盘形滚刀破岩实验台Fig.10 Straight-line rock breaking experiment bench of disc cutter

滚刀选用和数值模拟相同尺寸截面滚刀，直径为432 mm，刀刃宽为18 mm，刀刃为角20°，岩石长×宽×高为1 000 mm×500 mm×300 mm，力学参数如下：抗拉强度为5.69 MPa，抗压强度为100.33 MPa，弹性模量为11.45 GPa。在实验过程中，用带百分表的游标卡尺测量滚刀侵入深度，通过数据采集卡采集处理对应垂直力的数据。垂直液压油缸通过活动横梁不断向滚刀施压，使得滚刀贯入一定的深度，观察滚刀侵入岩石时的情形，量取侵入岩石深度。通过三向力传感器测量垂直力，表4所示为滚刀侵入深度对应垂直力的实验结果。通过实验结果可知，滚刀侵入深度越大，垂直力越大。

表4 垂直力实验测量结果Table 4 Experimental results of vertical force

5 结果对比

根据实验所用滚刀的尺寸参数以及岩石的宏观参数，可得数学预测模型计算结果，如表5所示。将岩石掘进机盘形滚刀侵入岩石的数学预测模型计算结果、数值模拟结果与实验结果进行对比，如图11所示。从图11可以看出，盘形滚刀侵入破岩垂直推进力随着侵入深度的增加而逐渐增大，数学预测模型计算结果与实验测量结果的误差随着侵入深度的增加而减小。这是由于在滚刀侵入岩石的初始阶段，岩石表面存在不平整性，进行滚刀侵入实验时，滚刀先是把岩石表面压平、压实，岩石内部的微裂隙被压紧或闭合，导致滚刀侵入深度较小时，实验测量的垂直力偏小，而数学预测模型没有考虑此因素，其计算结果偏大。滚刀侵入破岩的数学模型结果与数值模拟结果平均相对误差约为3.4%，与实验测量结果平均相对误差约为8.3%，数值模拟结果与实验结果平均相对误差约为12.1%，3种方法所得的垂直力比较接近，验证了受力预测模型的正确性和有效性。

表5 垂直力数学预测模型计算结果Table 5 Calculation results of mathematical prediction model of vertical force

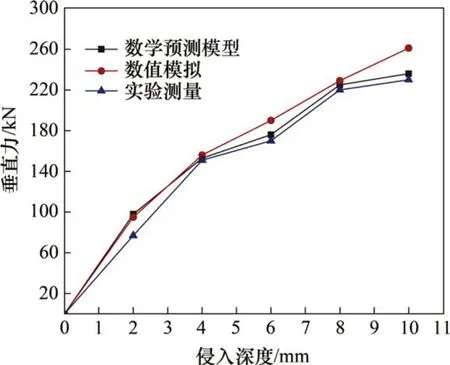
图11 滚刀侵入破岩垂直力对比图Fig.11 Comparison of vertical force of invading breaking rock model with disc cutter

6 结论

1)通过对滚刀侵入破岩机理进行研究，考虑密实核的性质，以摩尔-库仑理论为基础，建立了盘形滚刀侵入破岩的力学预测模型，得到了滚刀侵入破岩垂直推进力的表达式、滚刀侵入岩石垂直力的数学预测模型计算结果。

2)将数学预测模型计算结果与数值模拟结果、实验结果进行对比分析，发现这3种方法所得的垂直力比较接近，验证了模型的正确性和有效性。