气体状态变化中关联问题的处理
重庆 张大洪
选修3-3模块是高考的热学知识部分,是每年必考的模块,其中理想气体状态方程与气体实验定律知识点是本模块的重难点,一般分值在10分;封闭气体压强的计算则是该知识点中的最基本的问题,本文将气体状态变化中的关联问题分类探讨,希望能对广大中学生起到有效的指导作用。
1.液柱关联下的气体压强计算
【典例】已知大气压强为p0,图1所示的装置处于静止状态,液体密度均为ρ,各段液柱尺寸已标于图中,求被封闭的各段气体的压强。
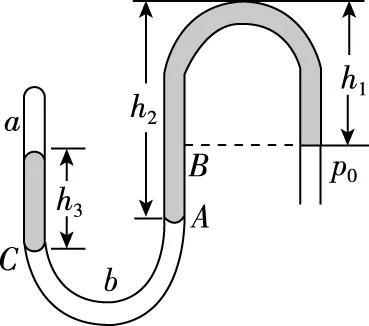
图1
【解析】对于图1中气体b而言,通过右边的弯曲液柱与大气相关联,关联的最低液面即为A面;又因为等高液面的压强必相等,即图1中pB=p0,那么由A面与右侧液柱的压强平衡pb=pA=pB+pAB,即pb=p0+ρg(h2-h1);对管内封闭气柱a而言,其将通过竖直液柱h3与气体b相关联,关联的最低液面为C面,由C面压强平衡pC=pb=pa+ph3,即pa+ρgh3=p0+ρg(h2-h1),故pa=p0+ρg(h2-h1-h3)。
【点评】由液柱关联下的气体压强处理:
(1)连通器内静止的同种液体(中间液体不间断)在等高液面(即在同一水平液面)处的压强大小一定是相等的;
(2)探讨由静止液柱封闭的气柱压强时,以与封闭气柱相关联的液柱的最低液面研究对象,利用该液面受到的向上、向下压力的平衡来处理;
(3)探求由非平衡状态的液柱封闭的气体压强时,以与气柱相关联的液柱为力学研究对象进行受力分析、用牛顿第二定律列出方程处理;
(4)准确把握好几何关系,找出辅助的相关关系;
(5)两部分气体的问题,要分别以两部分气体为研究对象,根据对应实验规律列方程。
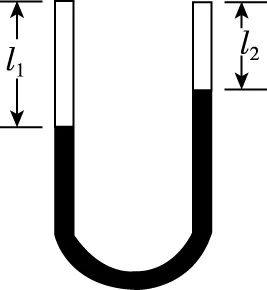
图2
【真题赏析】(2018年全国卷Ⅲ第33题)在两端封闭,粗细均匀的U形细玻璃管内有一段水银柱,水银柱的两端各封闭有一段空气如图2所示;当U形管两端竖直朝上时,左、右两边空气柱的长度分别为l1=18.0 cm和l2=12.0 cm,左边气体的压强为12.0 cmHg。现将U形管缓慢平放在水平桌面上,没有气体从管的一边通过水银逸入另一边。求U形管平放时两边空气柱的长度。在整个过程中,气体温度不变。
【解析】图2中U形管两端竖直朝上时,通过水银柱关联的左、右两部分气体中,水银柱的最低液面在左管,故对左管液面利用压强平衡有(设此时左、右两边气体的压强分别为p1和p2)p1=p2+ρg(l1-l2)。当U形管水平放置时,管中的水银柱必将向气体“2”的一侧移动并最终达到静止,如图3所示,此时两边气体压强相等设为p。

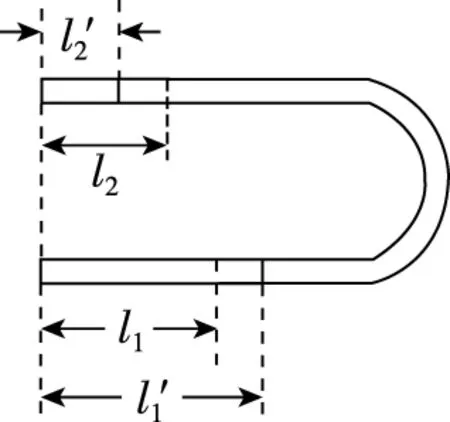
图3


由题给条件及①②③共同解得
【真题赏析】(2017年全国卷Ⅲ第33题)一种测量稀薄气体压强的仪器如图4(甲)所示,玻璃泡M的上端和下端分别连通两竖直玻璃细管K1和K2,K1长为l,顶端封闭,K2上端与待测气体连通;M下端经橡皮软管与充有水银的容器R连通。开始测量时,M与K2相通;逐渐提升R,直到K2中水银面与K1顶端等高,此时水银已进入K1,且K1中水银面比顶端低h,如图4(乙)所示。设测量过程中温度、与K2相通的待测气体的压强均保持不变。已知K1和K2的内径均为d,M的容积为V0,水银的密度为ρ,重力加速度大小为g。求:
(ⅰ)待测气体的压强;
(ⅱ)该仪器能够测量的最大压强。
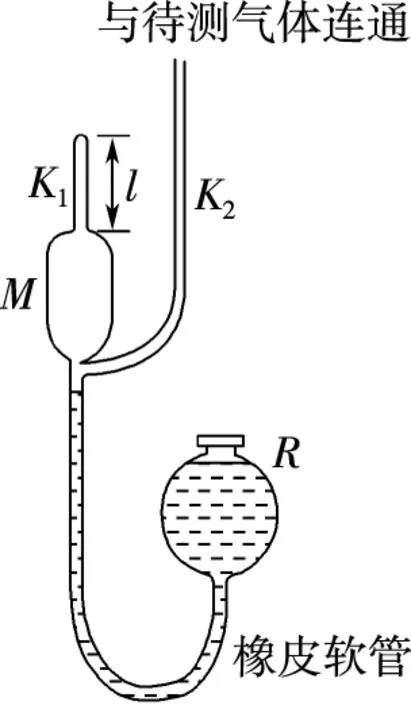
甲

乙

(ⅱ)由题意知h≤l根据“(ⅰ)”中的结果

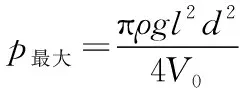
2.由单一活塞关联的气体压强问题
图5
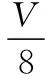


图6
【点评】由活塞关联下的气体压强处理:
(1)正确分析活塞的受力情况,结合活塞的运动情况由力的平衡或牛顿第二定律来探究压强的关联情况;
(2)两部分气体的问题,分别以两部分气体为研究对象,找出各自状态参量及其相关关系(注意图中的几何关系),然后根据相应的气体实验定律列方程。
【真题赏析】(2017年全国卷Ⅰ第33题)如图7所示,容积均为V的气缸A、B下端有细管(容积可忽略)连通,阀门K2位于细管的中部,A、B的顶部各有一阀门K1、K3;B中有一可自由滑动的活塞(质量、体积均可忽略)。初始时,三个阀门均打开,活塞在B的底部;关闭K2、K3,通过K1给气缸充气,使A中气体的压强达到大气压p0的3倍后关闭K1。已知室温为27℃,气缸导热。
(ⅰ)打开K2,求稳定时活塞上方气体的体积和压强;
(ⅱ)接着打开K3,求稳定时活塞的位置;
(ⅲ)再缓慢加热气缸内气体使其温度升高20℃,求此时活塞下方气体的压强。

图7
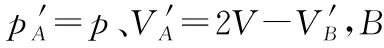
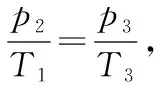
3.复式活塞关联下气体压强的处理
【典例】气缸由两个横截面不同的圆筒连接而成,活塞A、B被轻质刚性细杆连接在一起,活塞可无摩擦移动,活塞A、B的质量分别为m1=24 kg、m2=16 kg,横截面积分别为S1=6.0×10-2m2、S2=4.0×10-2m2,一定质量的理想气体被封闭在两活塞之间,活塞外侧大气压强p0=1.0×105Pa。
(1)如图8甲所示,气缸水平放置达到平衡状态时,求内部气体的压强。
(2)已知水平放置平衡时气体的体积V=2.0×10-2m3,现保持温度不变将气缸竖直放置,如图8乙所示,取重力加速度g=10 m/s2。达到平衡后,活塞在气缸内移动的距离为多少?(活塞A还未到达气缸连接处)

甲

乙
【解析】(1)由题知当气缸达到平衡状态即表明复式活塞系统必处于平衡,故复式活塞系统的受力必满足平衡条件,但需注意A、B的受力方向与面积大小;设平衡时气缸内气体压强为p1,对于复式活塞A、B系统受力如图8所示,由平衡条件有p0S1+p1S2=p1S1+p0S2,解得p1=p0=1.0×105Pa。

【点评】对复式活塞关联问题:
(1)选取复式活塞(含杆)整个连体为研究对象,正确对其进行受力分析;
(2)弄清复式活塞各面受到的压力方向与大小(含大气压力、封闭气体压力),利用力的平衡条件或牛顿第二定律列式探究压强关系;
(3)应用相应的气体实验定律联合求解。
【真题赏析】(2019年全国卷Ⅱ第33题)如图9所示,一容器由横截面积分别为2S和S的两个气缸连通而成,容器平放在地面上,气缸内壁光滑。整个容器被通过刚性杆连接的两活塞分隔成三部分,分别充有氢气、空气和氮气。平衡时,氮气的压强和体积分别为p0和V0,氢气的体积为2V0,空气的压强为p。现缓慢地将中部的空气全部抽出,抽气过程中氢气和氮气的温度保持不变,活塞没有到达两气缸的连接处,求:
(ⅰ)抽气前氢气的压强;
(ⅱ)抽气后氢气的压强和体积。

图9
【解析】(ⅰ)设抽气前氢气的压强为p′,左边活塞2S必受氢气对其水平向右的压力p′·2S、及空气对其水平向左的压力p2S作用,右边活塞S必受氮气对其水平向左的压力p0S、及空气对其水平向右的压力pS作用,根据力的平衡条件得(p′-p)·2S=(p0-p)·S,解得p′=(p0+p)。
(ⅱ)将空气抽出过程中由于空气压强不断减小,故空气对两活塞的压力也不断减小,因而复式活塞A、B系统合力必向右,故A、B系统必将向右边移动;设抽气后氢气的压强和体积分别为p1和V1,氮气的压强和体积分别为p2和V2,根据力的平衡条件有p2·S=p1·2S①,由于此过程温度保持不变,由玻意耳定律对氢气有p1V1=p′·2V0②
对氮气有p2V2=p0·V0③,在上述状态变化过程中氢气体积增加了V1-2V0,氮气体积减小了V0-V2,由于两活塞用刚性杆连接由题中的活塞面积大小关系故必有V1-2V0=2(V0-V2)④
【拓展】对于液柱或活塞封闭的气体,无论装置处于力学平衡状态或有加速度的非平衡状态,一般选择与气柱相关联的液柱或活塞为力学研究对象进行受力分析、列平衡方程或用牛顿第二定律列出方程。
4.一部分气体的多个关联过程问题

图10

(ⅰ)在大活塞与大圆筒底部接触前的瞬间,气缸内封闭气体的温度;
(ⅱ)缸内封闭的气体与缸外大气达到热平衡时,缸内封闭气体的压强。
【解析】由题意知封闭气体在缓慢变化中经历了两个过程,即从图10所示状态到大活塞与大圆筒底部接触前的状态、从大活塞与大圆筒底部接触状态到封闭气体与缸外大气达到热平衡的状态,两过程是通过大活塞与大圆筒底部接触前气体的状态相关联。

【点评】对多过程的关联问题要注意:
(1)阶段性:即弄清一个物理变化分为哪几个阶段;
(2)联系性:即找出几个阶段之间是由什么物理量联系起来的;
(3)规律性:即明确哪个阶段应遵循什么实验定律。
【总结】封闭气体的压强,不仅与气体的状态变化有关,还与相关联的液柱、活塞、气缸等物体的受力情况和运动状态有关,解决这类问题的关键有以下3点:
(1)明确研究对象(力学对象与热学对象);
(2)对力学对象(液柱、活塞、气缸等)进行正确的受力情况分析和运动运动情况分析,列出关于研究对象的力学方程,找出各热学对象间的压强关系;


