构建天体运动模型 突破能量问题瓶颈

福建 郭 威

2019年高考物理《考试大纲》总纲中有一些重要变化，特别是题型示例部分例12，由原来的2013年新课标全国卷Ⅱ第20题换成了2018年全国卷Ⅰ的第20题，换后的题用引力波这一最新的科研成果设计问题情境，主要考查考生的理解能力和推理能力，以引导考生关注宇宙、关注科学，提高学习科学的兴趣，培养科学精神，由此可见万有引力与航天在今后高考命题中仍是高考热点，而天体运动中能量问题却是该问题的一大难点。本文从高中常见的圆轨道与椭圆轨道构建天体运动能量模型入手，对航天器(飞船或卫星等)的发射、动能、引力势能及总能量的分析与计算进行模型构建，有效地突破能量分析与计算的瓶颈。

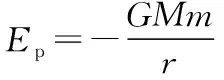
一、稳定圆轨道——稳定圆轨道模型(如图1中轨道1与轨道3)

图1

从圆轨道1到圆轨道3需要分别在近地点A和远地点B点火加速，对航天器做正功，外力所做的功等于两轨道的能量差，即W=E3-E1；反之从轨道3到轨道1，需要分别在远地点B和近地点A点火减速，对航天器做负功，所以外力做的功等于两轨道的能量差，即W=E1-E3。

【调研试题1】某卫星在半径为r的轨道1上做圆周运动，动能为E1，变轨到轨道2上后，动能比在轨道1上减小了ΔE，在轨道2上也做圆周运动，则轨道2的半径为

( )

( )

二、椭圆轨道——椭圆轨道模型(如图2中轨道2)

图2

在椭圆轨道上运行，从椭圆轨道2的A处运动到椭圆轨道2的B处过程中动能减小，引力势能增大，不考虑其他星体对它的作用，整个过程机械能守恒，有E2A=E2B或Ek2A+Ep2A=Ek2B+Ep2B；椭圆轨道2的A点和轨道2的B点之间是同一椭圆轨道，引力做的功或克服引力做的功等于两点间动能的变化量。

图3

【解题思路】返回舱与人在火星表面附近有

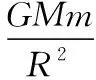
设轨道舱的质量为m0，速度大小为v，则

宇航员乘坐的返回舱获得能量后沿椭圆轨道与轨道舱对接，机械能守恒

因为返回舱返回过程克服引力做功

由②③④⑤得返回舱返回时至少需要能量

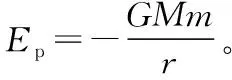
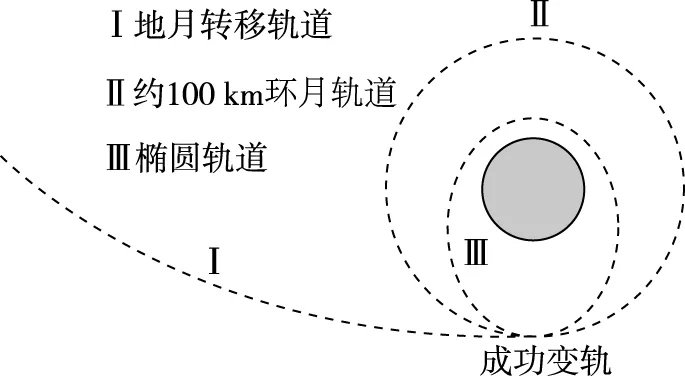
图4

(1)“嫦娥三号”在环月圆轨道上运行时的速率v；

(2)“嫦娥三号”在绕月椭圆轨道上运动时通过远月点时的速率v1。

(2)“嫦娥三号”在椭圆轨道上运动时只受月球引力作用，满足机械能守恒，由题意知“嫦娥三号”在近月点的速度为v0。根据机械能守恒有

三、稳定圆轨道——椭圆轨道模型(如图5中轨道1与轨道2或轨道2与轨道3)

抓培训，干部队伍素质进一步提升。林芝市局领导班子高度重视干部培训工作，积极组织干部赴成都、北京、拉萨、广东、福建等地参加“四品一械”相关培训，自主举办食品安全、食品药品抽样、食品药品安全协管员培训班等各类培训16期，参训人数共计2000余人次。

图5

【调研试题5】2018年1月12日，我国成功发射“北斗三号”组网卫星。如图为卫星发射示意图，先将卫星发射到半径为r的圆轨道上做圆周运动，到A点时使卫星加速进入椭圆轨道，到椭圆轨道的远地点B点时，再次改变卫星的速度，使卫星进入半径为2r的圆轨道。已知卫星在椭圆轨道时距地球的距离与速度的乘积为定值，卫星在椭圆轨道上A点时的速度为v，卫星质量为m，地球的质量为M，引力常量为G，则发动机在A点对卫星做的功与在B点对卫星做的功之差为

( )

图6

图7

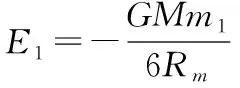
四、星球表面——近地稳定圆轨道模型(如图8中星球表面与近地轨道1)

图8

忽略星球自转的情况下，近地圆轨道引力势能近似等于星球表面的引力势能，从星球表面对航天器做的功W1=Ek，获得初动能后到近地圆轨道1，Ek=Ek1。如果要离开星球，能离开星球引力范围至少要运动到星球的零引力势能处，可分两个过程：一是从星球表面到星球表面圆轨道，外力对航天器做的功W2=Ek2，获得初动能Ek2(即第二宇宙速度时对应的动能)，二是星球表面圆轨道经椭圆轨道到无穷远处机械能守恒，即Ek2+Ep=0+0(Ep为近地引力势能)。

【解题思路】以无穷远处为零势能点，引力做的功等于引力势能的负值，即

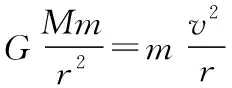
即由①②式可知圆轨道的总能量

将飞船从地面送入距地面高度为h的圆轨道运动过程中，可分为两个过程：

一是将飞船从地面送入地球表面圆轨道，火箭要对飞船所做的功为W1

二是地球表面圆轨道到离地高度为h的圆轨道，火箭要对飞船所做的功即距地面高度为h的圆轨道与地球表面圆轨道的能量差，由③式得

所以火箭要对飞船所做的功W=Ek1+ΔE⑥

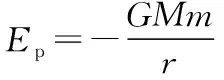
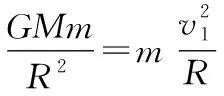
当卫星脱离地球吸引时，在无穷远处卫星势能为零，最低动能为零

由卫星发射后机械能守恒得