联合Capped范数极小化的子空间聚类算法*

涂志辉，陈 龙，张子长，朱雪芳，胡文玉

(赣南师范大学 数学与计算机科学学院，江西 赣州 341000)

1 引言

近年来，随着互联网发展迅速，数据收集变得越来越容易，最直接的结果是导致数据集变得越来越庞大和复杂，且这些数据通常由多种高维模式产生.然而，观测到的高维数据集通常源自于多个低维子空间的联合分布.因此需要一种能够查找多个低维子空间，并同时将数据聚类到不同子空间的技术.上述问题称为子空间聚类(Subspace Clustering, SC)，近年来备受关注，已经广泛应用于图像处理和计算机视觉等实际问题.

在最近的20年，许多子空间聚类方法被提出，包括迭代方法、代数方法、统计方法和谱聚类方法[1].其中，基于谱聚类的方法在处理实际数据时显示出了优越性.基于谱聚类的方法包括2个主要步骤：首先找到一个能刻画数据间拓扑关系的关联矩阵，然后基于该关联矩阵利用聚类方法将数据划分到不同的子空间中.假若数据满足自表达性，即原始数据中每一个样本能由其余样本线性表示，谱聚类的一般模型可以表述为：

(1)

其中X表示原始数据矩阵，Z表示系数(关联)矩阵，φ(·)和δ(·)分别表示数据拟合项和正则项，Δ为系数矩阵Z的约束条件，λ为正则项的参数.

谱聚类方法成功的关键在于关联矩阵Z的构建，常见方法有稀疏子空间聚类方法(SparseSubspaceClustering,SSC)[1]，低秩表示方法(LowRankRepresentation,LRR)[2]和自适应子空间分割方法(CorrelationAdaptiveSubspaceSegmentation,CASS)[3].其中SSC方法使用l1范数针对每个点找最稀疏的表示，LRR方法使用核范数去找低秩的关联矩阵，而CASS自适应考虑了数据间的相关性.然而，实际数据往往受到噪声的污染，并且噪声的统计分布十分复杂.正如[4-5]所指出，如果不能有效地描述噪声，系数矩阵将无法捕获数据间的内在拓扑关系，这将降低子空间聚类的性能.

为了解决这个问题，Lu等人[6]提出了通过cappedl1范数的鲁棒子空间聚类算法去惩罚噪声项，但该算法利用Frobenius范数作为矩阵秩的正则化，不能较好地逼近秩函数.针对上述问题，本文提出联合capped范数极小化的子空间聚类算法(JointCappedNormsMinimizationforSubspaceClusering,CNSC)，使用capped核范数代替Frobenius范数，使模型能较好地刻画数据的低秩性，同时对数据噪声和异常值鲁棒.

2 相关工作

稀疏子空间聚类方法(SSC)[1]试图寻找每个数据点的稀疏表示，其模型在数学上可表述为：

(2)

SSC方法的不足是SSC单独寻找每个数据点的稀疏表示, 所得的矩阵Z可能过于稀疏，从而导致过度分割.

低秩表示方法(LRR)[2]目标是共同寻求所有数据的最低秩表示，LRR模型的优化模型表为：

(3)

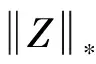
Lu等人[7]提出最小二乘回归方法(LeastSquaresRegression,LSR).该方法采用Frobenius范数来替代秩函数，所得模型是：

(4)

可以证明，当数据来自独立子空间且无噪声时，SSC，LRR和LSR均可以得到块对角型的系数矩阵Z.这些方法主要聚焦于关联矩阵的构造，而忽视了噪声对聚类性能的影响.然而，真实数据总是会受到噪声或异常值的污染，通过上述求解方案得到的关联矩阵可能并不是块对角的.

最近，Lu等人[6]利用cappedl1范数作为噪声惩罚项，来提升聚类结果对噪声的鲁棒性.其优化模型如下：

(5)

3 联合capped范数的子空间聚类

首先介绍capped核范数的定义，然后给出联合cappedl1范数和capped核范数的聚类模型和求解算法，最后给出算法的收敛性证明.

3.1 capped核范数定义

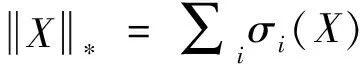
(6)

由定义可知，相比于核范数，capped核范数是秩函数更好的近似.这是因为：当矩阵的最大奇异值不断变大时，矩阵的秩始终保持不变，但是矩阵的核范数却会随之发生很大改变.另一方面，由于capped核范数仅仅最小化小于ε的奇异值，故而奇异值的极端变化不会改变，甚至仍保持capped核范数的值.

图1给出了函数f(x)=min(|x|,ε)的函数图像，其中取ε=1.如图所示，f(x)在(-∞,-1)∪(1,+∞)区域上保持常值.可知，通过选择合适的ε，capped核范数能减少矩阵大奇异值对子空间聚类性能的影响.

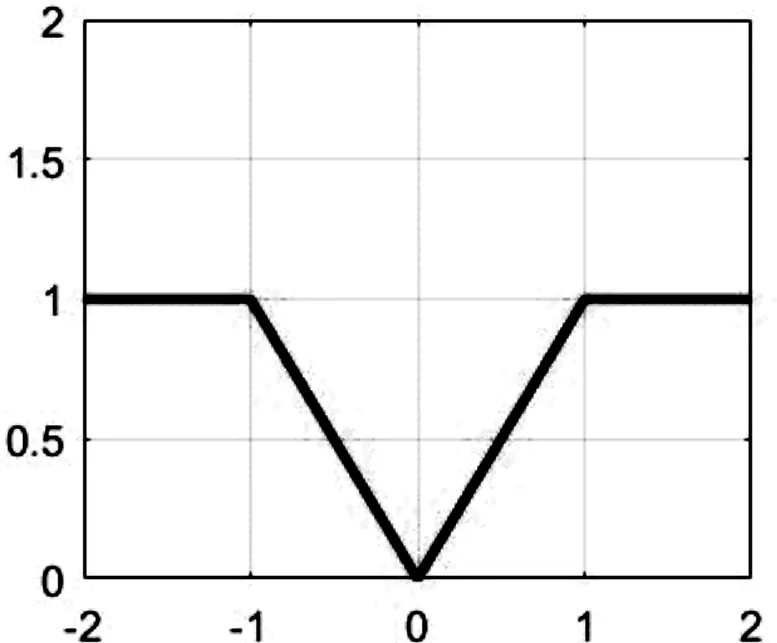
图1 capped函数f(x)的函数图像(ε=1)

3.2 子空间聚类模型

我们联合矩阵的cappedl1范数与capped核范数建立如下的子空间聚类模型(CNSC)：

(7)

特别地，式(7)可以等价写为：

(8)

其中n表示数据样本的个数，xi∈Rd表示数据矩阵X的第i个样本向量，zi表示关联表示向量，r=min(d,n).从式(8)可以看出，当ε1,ε2趋于无穷大时，目标函数变成了LRR模型，说明LRR方法是本文的一个特例.

问题(8)的求解看似非常困难，因为式(8)的两项都是凹函数.然而，受重加权(re-weighted)技巧的启发[8]，这个问题能够简单地得以解决.首先，构造辅助变量D、si，并且使用下列的规则依次更新si、D和Z：

(9)

(10)

(11)

其中Z=U∑VT表示矩阵Z的奇异值分解，U=[u1,u2,…,ud],V=[v1,v2,…,vn],∑=diag(σ1,σ2,…,σr),奇异值σi从小到大排列，假设小于ε2的奇异值个数为k.

为求解子问题(11)，我们将它分解成n个独立的子问题.具体的计算过程如下：

(12)

(13)

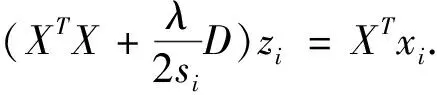
(14)

3.3 求解算法

通过上述分析，问题(7)和(8)的最优解可以通过迭代方法求得.我们将整个迭代过程描述成如下算法：

算法1联合capped范数的子空间聚类(CNSC)算法

输入 数据矩阵X，最大迭代数kmax，参数λ、ε1、ε2,k=1,Z0=单位矩阵；

输出 系数矩阵Z.

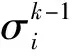
Step 3 根据式(14)更新Zk；

Step 4 若k≥kmax或收敛，输出结果；否则，k=k+1，转至step 1.

3.4 收敛性证明

受文献[10]启发，本小节证明算法1的收敛性.为此，需要引入如下几个引理：

引理1[9]对两个任意给定的Hermitian矩阵A、B∈Rn×n，假设它们的特征值满足λ1(A)≤λ2(A)≤…≤λn(A),λ1(B)≤λ2(B)≤…≤λn(B)，则

(15)

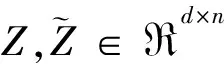
(16)

于是，我们有

其中第一个不等式利用了凹函数性质，最后一个等式利用了特征值与矩阵迹的关系，而最后一个等式利用了引理1中式(15)的前半部分.移项即得式(16).

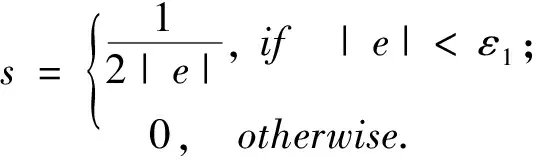
(17)

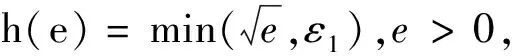
于是根据凹函数的性质，可得

移项整理后，得式(17).

定理1通过算法1，目标函数(8)随着迭代的进行而单调递减，直到收敛.

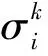
由Dk-1的定义，上式可改写为

(18)

也即

(19)

(20)

依次累加式(18)(19)和(20)的两边，从而得到：

最后，由于目标函数(8)有下界0，故算法1必收敛.

4 数值实验

将CNSC和3种经典的聚类方法进行对比，即稀疏子空间聚类方法(SSC)[1]、低秩表示子空间聚类方法(LRR)[2]，cappedl1范数子空间聚类算法(cappedl1)[6].实验中，使用准确率(Accuracy，ACC)作为算法性能的衡量指标：

(21)

其中ri表示xi的各类算法预测的聚类标签，li表示真实的聚类标签，n表示子空间数量.为了保证实验对比的公平性，所有算法都独立进行10次实验，比较各算法运行结果的平均值.

根据式(8)，本文的算法需要调整3个参数ε1,ε2,λ.我们参照文献[10]提到的方法进行调整.

4.1 合成数据

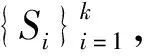
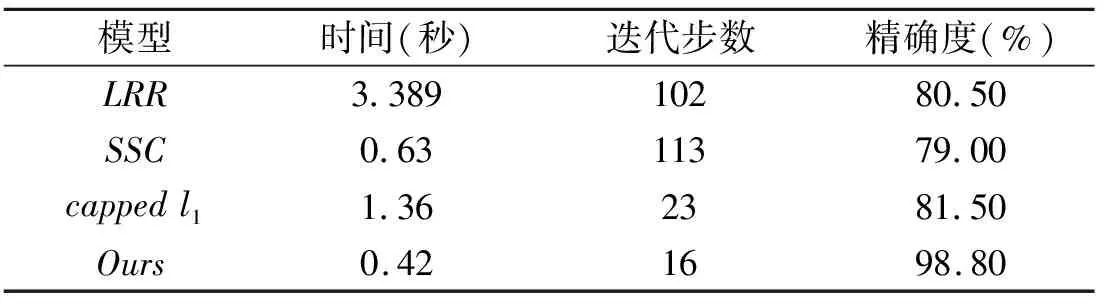
表1 四种方法聚类效果比较(合成数据)

由图2可知，本文提出的算法在噪声影响下仍可获得清晰的分块对角型系数矩阵，LRR和SSC方法都无法保持正确的块对角结构.相比之下，cappedl1和本文提出的CNSC算法拥有良好的分块对角特征，但是CNSC对角矩阵块更稠密.

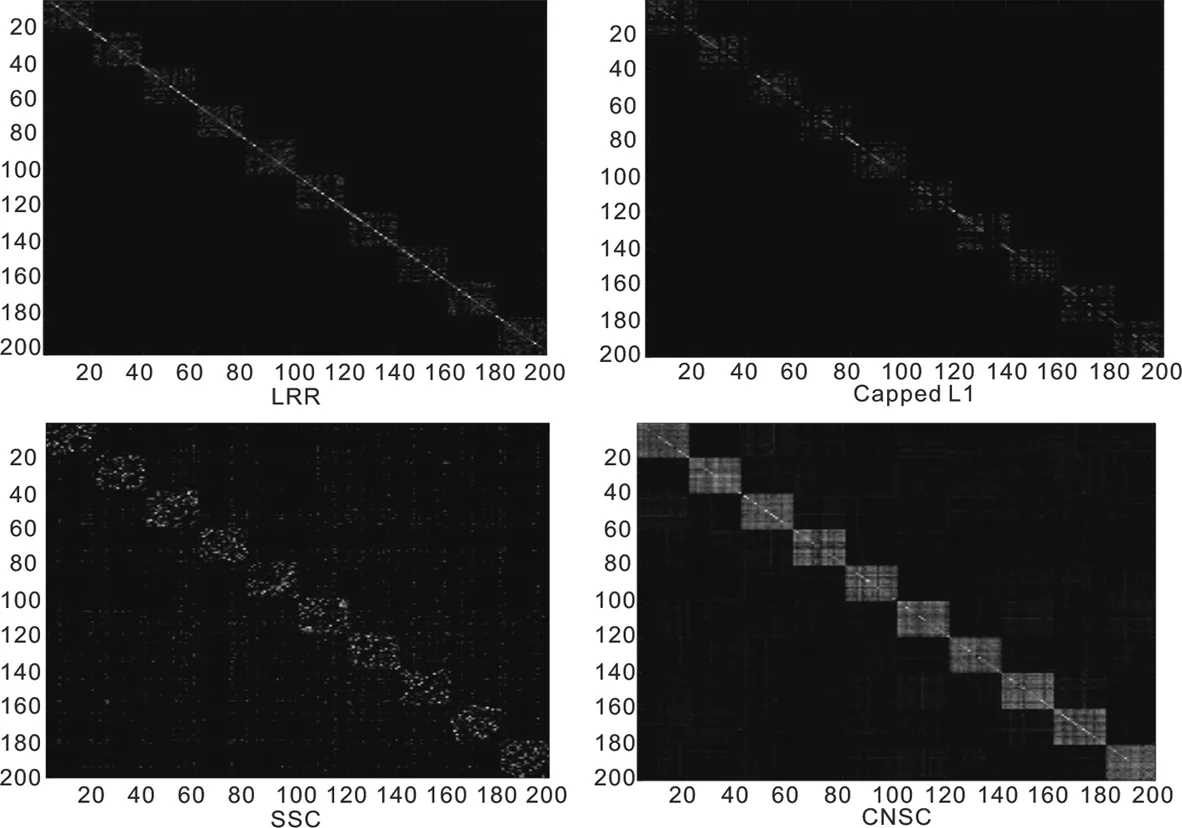
图2 4种算法在合成数据上的关联矩阵对角特征比较

4.2 人脸数据聚类

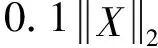
图3 数据集部分例子

从表2和表3可以看出，在真实数据含有噪声和异常值的情况下，本文提出的CNCS方法迭代步数少，精确度最高.说明本文提出的算法聚类性能较好且对异常值鲁棒.

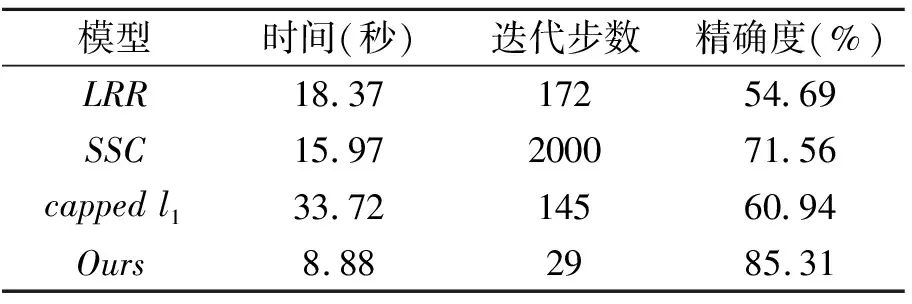
表2 4种方法在人脸集的聚类效果比较(5类)

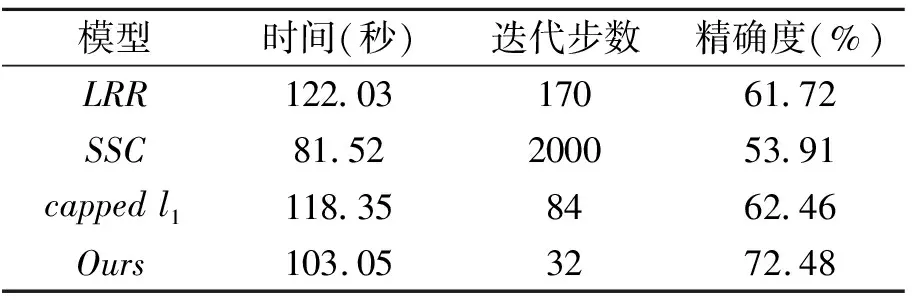
表3 4种方法在人脸集的聚类效果比较(10类)

5 结束语

本文提出了一种联合capped范数的子空间聚类算法(CNCS)，即分别使用cappedl1范数处理数据噪声和异常值和capped核范数逼近数据的低秩性.而且，通过数值实验，说明了本文算法的优越性.将来，我们将把本文算法推广至时序数据的子空间聚类问题.