指数为2的幂零矩阵的二次矩阵方程的反交换解*

武红光，周端美，丁佳文

(赣南师范大学 数学与计算机科学学院，江西 赣州 341000)

1 引言

令A是一个给定的n×n的复数矩阵,满足A2=0.本文主要是求解非线性二次矩阵方程

AXA=XAX

(1)

的所有反交换解,其中X是一个未知需求解矩阵.反交换解就是解X与矩阵A是反交换,即解X满足AX=-XA.方程(1)也被称为Yang-Baxter矩阵方程,因为它在形式上和经典的Yang-Baxter矩阵方程[1-2]相似.Yang-Baxter方程首次由诺贝尔奖得主杨振宁教授在理论物理学[3]中和R.J.Baxter在统计力学[1]中各自提出.后来该方程成为数学物理学中的一个基本方程,更确切的说是量子群理论的入门的基本方程[3],同时在扭结理论、量子场论、C*-代数、环链不变量、量子群、保形场论和非交换几何中起着至关重要的作用[3-5].Yang-Baxter方程有多种形式,最简单的是常数Yang-Baxter方程,这是由N2×N2矩阵R为元素的N6三次方程组,其形式为R12R13R23=R23R13R12.一个更复杂的Yang-Baxter方程形式是矩阵R依赖一个或两个参数R12(u)R13(u+v)R23(v)=R23(v)R13(u+v)R12(u).很多科学家对Yang-Baxter方程已求得多种解,比如通过定性方式或定量方式.但是,对所有不同类型的解仍然是悬而未决的问题.

近年来,由于它与纯数学领域(例如原始方程)的密切联系,引起了该研究的众多数学家的关注,并将Yang-Baxter方程简化成(1)式的非线性二次矩阵方程.对于各类已知矩阵已经找出了方程(1)的部分解[6-11].目前大多数解是交换解.虽然在不同的情况下对解的结构有许多结论,但至今还没有一般理论和方法来求解二次矩阵方程(1).

要找到方程(1)的解,一种常用的方法是通过对矩阵A的Jordan标准型结构来求解.最简单的非平凡Jordan块是特征值为0的2×2块矩阵.即使在这种特殊情况下,目前还没有关于一般反交换解的结果.当A是一个指数为2的幂零矩阵时,即A2=0,本文将求解矩阵方程(1)的所有反交换解.

2 A2=0的反交换解

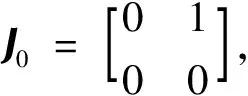
W-1AW=J≡diag(0,J0,…,J0),

其中W是非奇异矩阵,0是(n-2k)×(n-2k)零矩阵,J0的个数有k个.显然J中J0的个数等于A的秩.本文后面总是假设A的秩为k.通过文献[8]可以知道,如果J是A的Jordan标准型,那么求解非线性二次矩阵方程(1)就可以转化为求解一个简化的非线性二次矩阵方程,即用A的Jordan标准型来替代A.

引理1如果两个矩阵A和X满足AXA=XAX和AX=-XA,那么对于任意非奇异矩阵W,矩阵B=W-1AW和Y=W-1XW满足BYB=YBY和BY=-YB.反过来说,如果B=W-1AW,Y是上述方程的解,则X=WYW-1满足AXA=XAX和AX=-XA.

证明若B=W-1AW和Y=W-1XW,则由AXA=XAX和AX=-XA得WBW-1WYW-1WBW-1=WYW-1WBW-1WYW-1和WBW-1WYW-1=-WYW-1WBW-1.即BYB=YBY和BY=-YB.

反之,若B=W-1AW满足BYB=YBY和BY=-YB,则W-1AWYW-1AW=YW-1AWY和W-1AWY=-YW-1AW,即AWYW-1A=WYW-1AWYW-1和AWYW-1=-WYW-1A.因此,X=WYW-1满足AXA=XAX和AX=-XA.证毕.

非线性二次矩阵方程(1)的所有的解的具体形式目前还没有找到,它的结构也不清楚.即使系数矩阵A满足A2=0也不清楚.令J2,k=diag(J0,…,J0),其中k是J2,k中J0的个数.非线性二次矩阵方程J2,2YJ2,2=YJ2,2Y等价于一个多项式方程组

所以即使低阶的非线性二次矩阵方程(1)在A2=0条件下也是不易求解.

接下来将给出本文的主要定理,即在A2=0条件下,给出非线性二次矩阵方程(1)的所有反交换解的结构.

定理1令A是一个指数为2,秩为k的n阶幂零矩阵,且W-1AW=J=diag(0,J2,k).则非线性二次矩阵方程(1)的所有反交换解为X=WYW-1,其中

(2)

M∈C(n-2k)×(n-2k),u2i,v2i-1∈(n-2k),cij∈,i,j=1,2,…,k任意.bij∈,i,j=1,2,…,k构成的矩阵

满足B2=0.

证明由引理1知,求解AXA=XAX,AX=-XA可以转化为求解JYJ=YJY,JY=-YJ,其中Y=W-1XW.把Y分成与J相同的分块矩阵

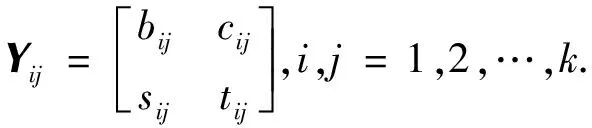
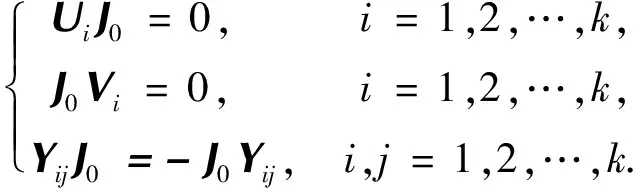
由非线性二次矩阵方程JYJ=YJY及UiJ0=0和J0Vi=0,i=1,2,…,k可得

由上式知,矩阵M任意,且

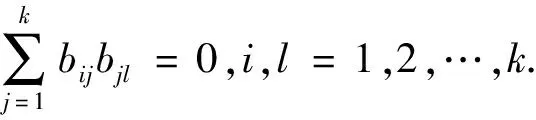
满足B2=0.综上可得(2)式解的结构.证毕.

注记1若A=J2,2,则A的Jordan标准型就等于它本身.根据定理1可得非线性二次矩阵方程(1)的所有反交换解为

满足AX1A=X1AX1=0,但是AX1≠-X1A.

3 结论

当系数矩阵A是一个指数为2的幂零矩阵,通过对幂零矩阵的性质分析给出A的Jordan分解A=WJW-1及相应的Jordan矩阵J的结构.然后将非线性二次矩阵方程AXA=XAX的求解转化成JYJ=YJY.同时将反交换解条件AX=-XA转化为JY=-YJ.基于JYJ=YJY和JY=-YJ及其J和Y分块形式,最终找到Y的解的结构.最后得到了非线性二次矩阵方程AXA=XAX的所有反交换解.本文的方法和技巧也许可运用于求解在A3=0条件下非线性二次矩阵方程(1)的所有反交换解，甚至可能推广到在Ak=0(k∈+)的条件下求解非线性二次矩阵方程(1)的所有反交换解.这将是以后的一个研究方向.