磨光化方法在数值微分中的应用*

向晓燕，徐会林，肖宇辉

(赣南师范大学 数学与计算机科学学院, 江西 赣州 341000)

1 引言

数值微分, 即利用函数在一些离散点上的测量值近似求其导数,是一类典型的不适定问题[1].众所周知,测量数据不可避免的会带有误差,这就使得近似导致的计算误差可能是任意大的.为克服数值微分问题的不适定性,尤其是这种不稳定性,必须引入求解不适定问题的稳定化算法.常见的稳定化算法有正则化方法[2-3]、有限差分法[4]、积分算子法[5]、磨光化方法[6]等.

磨光化方法是在求导之前对函数进行磨光,然后对磨光后的函数直接求导得到函数近似导数的一种方法.磨光可以去除待求导函数的高频噪声,保证近似导数的稳定性.这里的磨光一般是借助与核函数的卷积实现的,高斯核函数就是常用的磨光核函数[7].

本文首先在已有磨光化方法理论的基础上,分别在2种范数(∞范数和L2范数)下给出磨光核函数的通用选取准则以及相应近似导数的误差估计；其次,给出了2种磨光核函数的具体取法以及相应近似导数的误差估计；最后,通过数值算例说明了磨光化方法的可行性及数值有效性,并对2种磨光核函数的取法进行了比较实验.

2 磨光化方法

在介绍磨光化方法之前,首先给出磨光核函数的定义.

考虑函数f(x)的扰动数据fδ(x),则有

(1)

(2)

另一方面,我们有

(3)

由(2)和(3)式可得

(4)

接下来将在L2范数下估计近似导数Rσfδ(x)的误差.引入变换的定义:

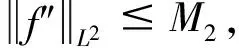
证明首先,近似导数Rσfδ(x)在L2范数下的误差满足:

(5)

计算可得

由F[f′]=itF[f]可知

(6)

由(5)和(6)式可知

(7)

3 磨光核函数的取法

除了正则化参数σ的选取外,磨光核函数的取法也起着至关重要的作用,最常见的取法是高斯核函数,参见文献[6-7].事实上,只要磨光核函数的取法满足定理1或定理2的条件,就可以得到近似导数的误差估计以及正则化参数的先验取法.接下来将验证高斯核函数满足定理1和定理2的条件.此外,还将给出磨光核函数的另一种取法——有理核函数,并证明其也满足定理1和定理2的条件.

3.1 高斯核函数

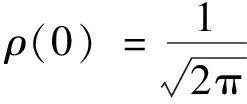
因此,由定理1及定理2可知

3.2 有理核函数

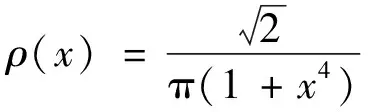
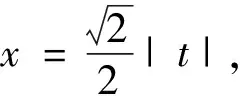
将区间(0,+∞)分成(0,1)和[1,+∞)两个区间进行讨论:

4 数值实验

考虑函数f(x)=sin(πx)k,x∈[0,1],则f′(x)=kπkxk-1cos(πx)k.对f(x)添加服从均匀分布的随机噪声得扰动数据,即fδ(x)=sin(πx)k+δ·rand(x),x∈[0,1].不难发现,k的取值越大,函数f(x)及其导数的震荡性也越强.下面,我们将分别对高斯核函数和有理核函数的磨光化方法考察近似导数的数值有效性.

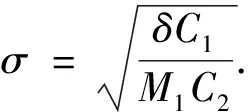
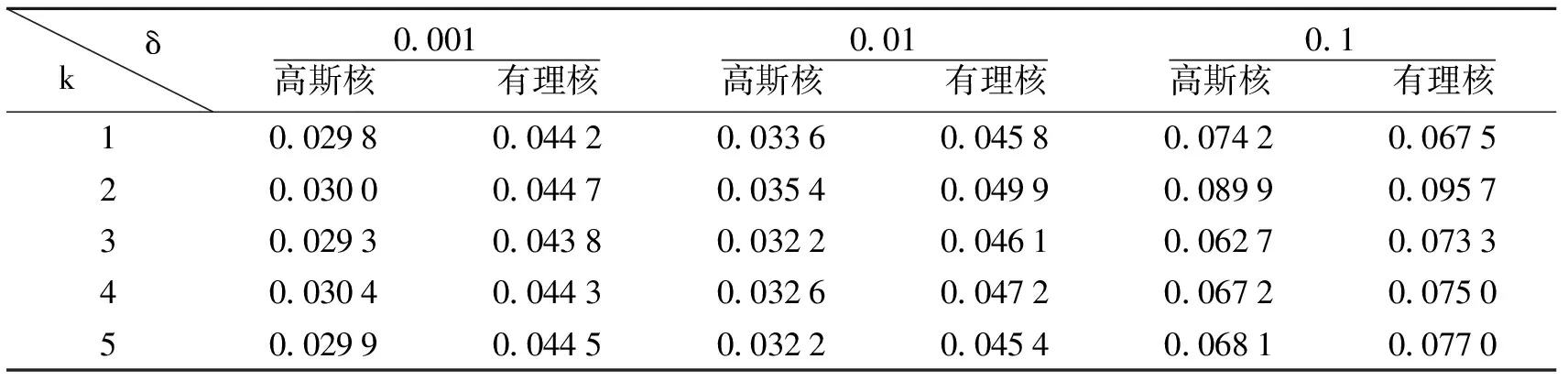
表1 当参数k和误差水平δ取值不同时,两种磨光核函数对应近似导数的相对误差

考虑高斯核函数磨光,当δ=0.001,k=3,4,5时,图1给出了精确导数与近似导数的图像,从中可以看出,无论精确导数的震荡性有多强,近似导数总能很好的逼近精确导数.

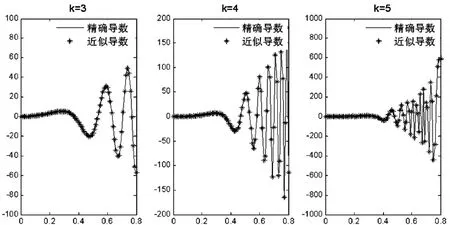
图1 当δ=0.001,k=3,4,5时,精确导数与高斯核函数磨光得到的近似导数的图像

5 总结

在求解数值微分问题的磨光化方法中,本文分别在2种范数(∞范数和L2范数)下给出了磨光核函数的通用选取准则以及相应近似导数的误差估计.在此基础上,给出了2种满足要求的磨光核函数:高斯核和有理核函数.数值实验表明了磨光化方法的数值稳定性以及对强震荡函数求导的数值有效性.数值算例也表明高斯核磨光比有理核磨光的效果更好.