黄河下游高村-陶城铺河段边界阻力能耗与河床稳定性分析

白玉川，李 岩，张金良，白 洋，冀自清

（1.天津大学 河流海岸工程泥沙研究所，天津 300072；2.黄河勘测规划设计有限公司，河南 郑州 450003）

1 研究背景

河流是一个具有自我调整的动态系统，不同时期不同空间所展现的形态（蜿蜒、游荡或顺直）是河流本身为了适应周边环境变化进行的多方面调整。河流行进过程伴随能量和物质的输入与输出，不断地进行能量传递与转换，沿程调整河床形态因子、水力因子、泥沙因子等，调整过程中能量耗散保持最小的趋向性[1]。

运用能量耗散理论研究河流工程泥沙问题成为水利工程领域一个热门研究方向，早期杨志达[2-3]提出的河流最小能耗率和张海燕[4-5]的最小河流功，认为河流处于平衡态时河流能耗率或河流功将达到最小，并用以预测冲积河流在平衡状态下的断面形态。后来众多学者运用能耗理论从河流能量损失、挟沙水流能量转换、河型演化等方面进行较为深入的研究。庞炳东[6]用流体力学的动能方程解释了主槽内能量损失的物理原因，描述了滩槽间动量交换的物理图形，并分析洪水漫滩对流场能量重分布的影响；舒安平等[7]基于两相挟沙水流紊动能量平衡方程，推导出紊动能转化率及泥沙悬浮效率系数，探讨了紊动能转化率、泥沙悬浮效率系数和泥沙悬浮功等随含沙浓度的变化规律。陈绪坚等[8]提出了保持冲积河流稳定的最小能耗率原理和公式，建立河道输水输沙优化数学模型；徐国宾等[9-10]则基于广义流和广义力推导出河流能耗率，并用于研究黄河下游河型变化与河道演变问题；孙东坡等[11]运用能量耗散关系对黄河内蒙段河床形态调整进行了系统地分析。本文第一作者从河流阻力方面研究了河床底沙运动，并基于河流阻力能耗与河流形态的辩证关系，引入河流形态参数，给出河流阻力参数与活动指标的河型判别法[12-14]。

本文基于以往的研究基础，从河流阻力角度出发，获得边界阻力能耗率公式；根据实测资料数据分析高村-陶城铺河段断面形态、深泓摆动以及沿程纵比降等变化特征；基于不同年份的河道地形，采用一维水动力数学模型计算出沿程各断面水面宽、水深、比降等水力要素值，计算不同年份河道的边界阻力能耗率，引入河床稳定性指标，探究阻力能耗率与河床断面形态、河床稳定性相关关系。

1 研究河段概括与研究方法

1.1 河段概括黄河下游河道从河南省孟津县进入平原，于山东省垦利县注入渤海，长约900 km，河道平面形态上宽下窄（最宽处达24 km，最窄处275 m），沿程比降上陡下缓，排洪能力上大下小（花园口22 000 m3/s，孙口17 500 m3/s，艾山11 000 m3/s）。黄河下游孟津白鹤-高村为游荡性河段，高村-陶城铺为过渡性河段，陶城铺-利津为弯曲性河段，利津以下为河口段。本文研究范围为高村-陶城铺河段（图1），长约154 km，河道比降0.118‰，弯曲系数1.26（弯曲系数是流路实际长度与起止点直线距离的比值），过渡性河段同时包括游荡性河段和弯曲性河段的特性。

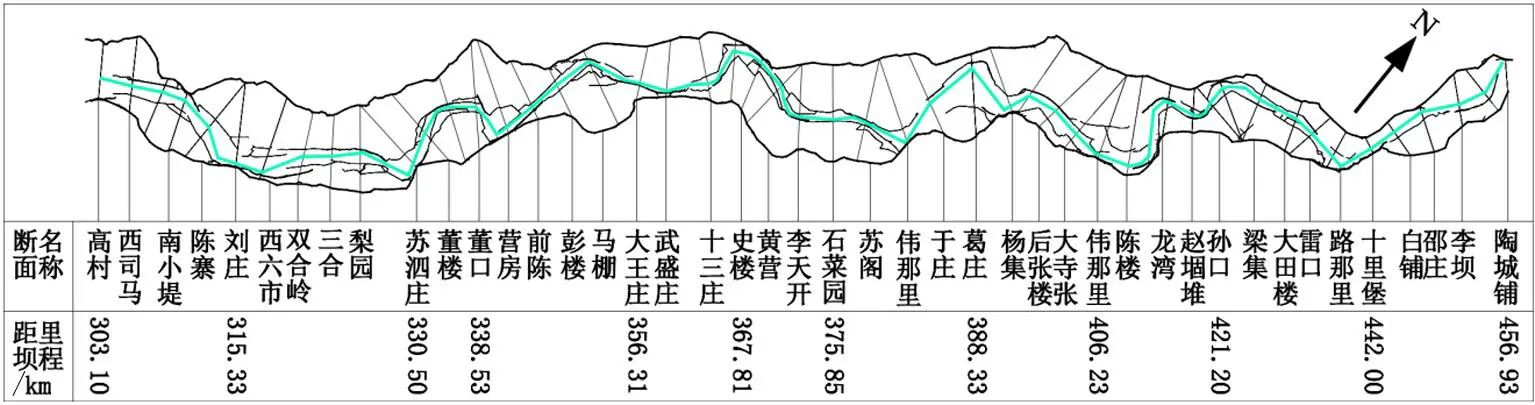
图1 黄河下游高村-陶城铺河段形态

本次主要采用2005年和2016年汛前河道地形及汛期水位、流量资料，由于该河段只有高村、孙口两处测站水位、流量数据，资料较少，故借助一维水动力数学模型，计算出高村-陶城铺河段各断面的水深、水面宽、过水断面面积、比降、流速等数据，分析流量分别为1000、2000、3000和4000 m3/s条件下高村-陶城铺河段的边界阻力能耗率变化情况以及与断面形态、河床稳定性之间关系。

1.2 边界阻力能耗率河流行进过程需克服边界阻力耗能，为适应周边外界环境变化不断调整自身形态以实现能耗转换与传递。在冲积河流系统中能量是一个转换耗散的过程，存在不同形式的能量耗散[15]，其中克服阻力耗能是能量耗散的主要来源。河流在行进过程中会受到不同形式的阻力，包括床面阻力、水面空气阻力、河道形态阻力等，这些阻力又统称为河流边界阻力，水流克服摩擦阻力而消耗能量即为边界阻力耗能。

在给定条件下，通过对剪切应力与流速梯度乘积进行积分可以获得能量耗散率P。在忽略张力对河床、河岸或水面的线性变形后，考虑流体是不可压缩且无旋情况，能量耗散率的形式可表示为[16]：

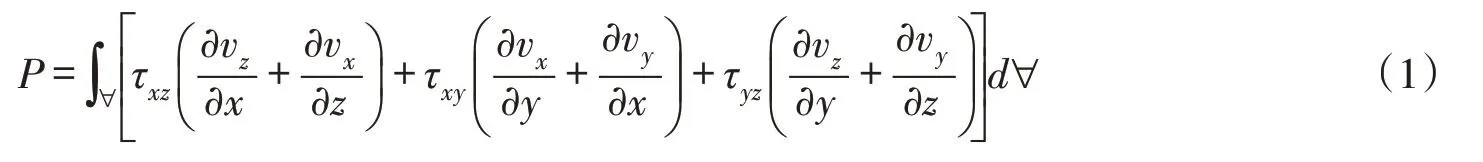
本研究假设流体为一维流情况（即vy =vz =0），且忽略二次环流引起的横向剪切应力变化，即τzy =0，

则式（1）可以化简为：

式中：τzx为垂向剪切应力，其中水面剪切应力τw=0，τzx=τb；对于宽浅河流，忽略河岸剪切应力τyx的影响，式（2）化简为：

式中：L为河段长度；χ为河床湿周；u为明渠水流垂线平均速度。

对明渠均匀流来说，河床边界剪切应力公式可写成：

式中，λ为阻力系数，可用谢才系数C来表示，即代入上式（4）得：

式（5）代入式（3）整理后，得到单位河段边界阻力能耗率：

式（6）为考虑了河流综合阻力的能耗率公式，其中C为谢才系数，也为综合阻力系数；ρ为密度；g为重力加速度；Q为流量；R为水力半径；A为过水断面面积。

1.3 一维水动力数学模型的验证利用一维水动力模型模拟高村至陶城铺河段的水流，其基本方程包括连续方程和运动方程。基于2005年和2016年黄河下游汛前地形和汛期实测水位、流量资料，以汛期（6月15日—10月15日）高村站流量作为入口条件，艾山站水位作为出口条件。其中模型采用的糙率为n=aub，其中a为系数，b为指数，而a值参考a=R23J12选取，J为比降。根据程进豪等[17]对黄河山东段河床糙率分析结果得到，糙率呈带状分布，黄河下游河道各站不同时期糙率随流量变化的总趋势是相同的，当流量很小时，糙率值较大，且随着流量增大，糙率逐渐减小。

选取孙口站水位资料作为验证条件，验证结果如图2所示，其中圆圈是实测值，实线为计算值，通过对比发现计算值与实测值最大误差不超过0.1 m，验证效果整体较好，可以支撑后续方案模拟。

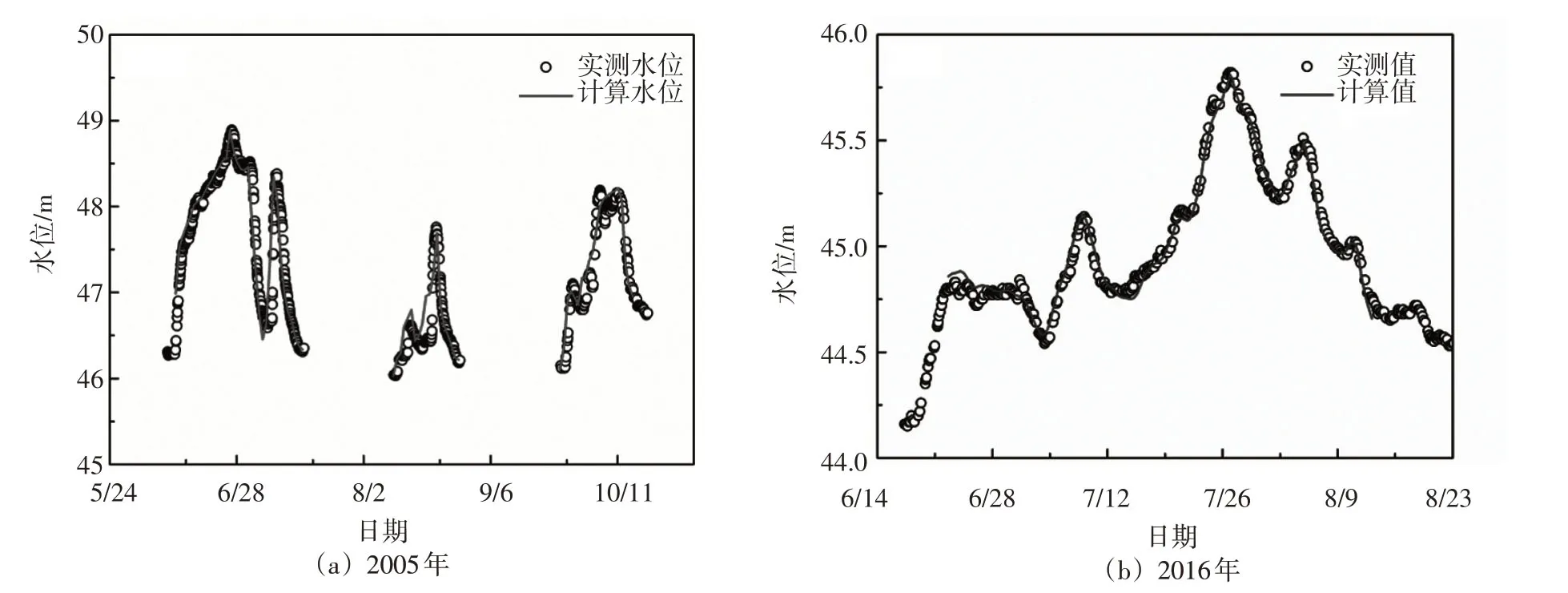
图2 黄河下游孙口站水位验证

2 河床形态调整过程及边界阻力能耗率响应关系

2.1 河床形态调整分析河床形态可分为横断面形态、纵剖面形态和平面形态，横断面形态量化方法有槽宽、槽深、断面面积、湿周及宽深比等，纵剖面表现形式主要体现在沿程河床比降的变化，而平面形态的量化方式有弯曲系数、曲率半径、弯距、摆幅等[18]。黄河下游为典型的复式断面河道，横断面形态复杂，其中滩地宽阔具有滞洪沉沙的功能，主槽区域是输水输沙的主要通道。本次我们主要从河槽深泓的平面摆动、横断面变化及沿程纵向比降三个方面来探讨河床形态调整规律。

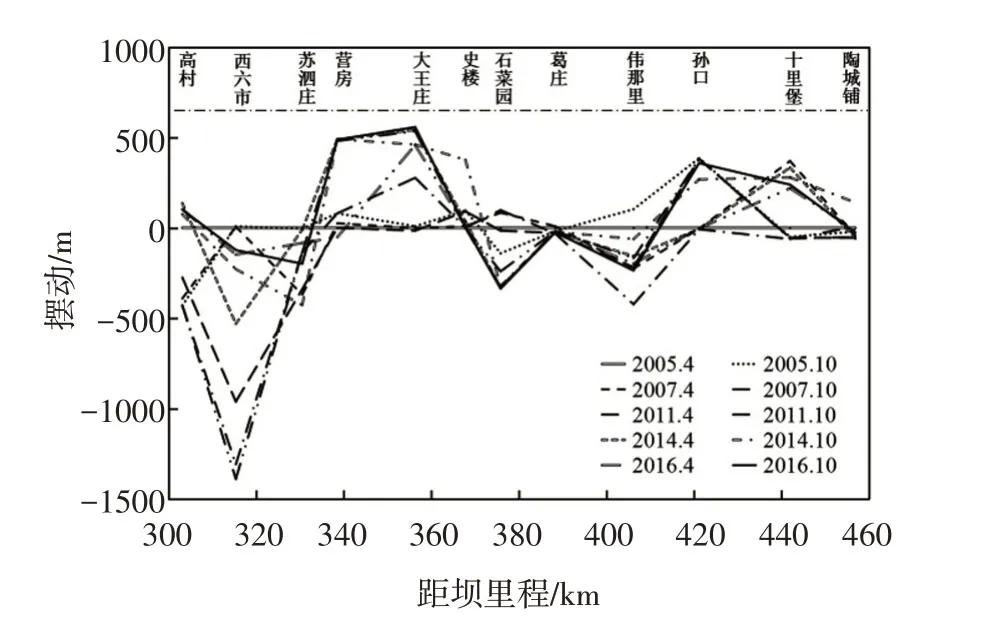
图3 以2005年汛前地形为基准深泓左右摆动情况

图4 高村-陶城铺河段沿程比降及部分主槽断面形态

河床平面活动性与河流能量的沿程分配有关，主要通过弯曲系数、深泓点摆幅及断面形态等方面来体现能量的沿程耗散特性[11]。这里以2005年汛前深泓为基准，根据实测数据资料统计了高村-陶城铺河段从2005到2016年实测断面深泓点摆动情况，如图3所示（向左摆动为负值，向右摆动为正值）。从不同时期的对比情况可以看出，不同年份河床横向摆动幅度差别较大，其中高村断面深泓的平均摆动幅度可达263 m，孙口断面为200 m，而陶城铺断面仅为46 m。深泓的摆动幅度受汛期来水来沙影响较大，汛期冲淤量越大，深泓的摆动幅度也越大。随着河流向下游推进，其平面摆动幅度是呈减小趋势，河床断面对水流的束缚力增强，河床抗冲刷性也得到显著提高。

水沙条件的变化不仅影响河道深泓的摆动，同时也对横断面形态有着重要作用。黄河下游河床冲刷时主槽横断面形态的调整取决于河道特性、河段位置，既有可能出现断面展宽，又有可能出现断面趋于窄深[19]。小浪底水库运用以来，由于低含沙水流的长期下泄，黄河下游河道多年冲刷下切导致河床不断粗化，冲刷强度减弱，河道展宽逐渐明显，其中高村、董口和孙口断面处在相对顺直的河道（图1），同时存在下切冲深和展宽侵蚀（图4），河槽形态更趋近梯形断面；而葛庄和陶城铺断面处在弯道的顶点位置，主要以下切冲深为主，两侧侵蚀较少，主槽断面形态偏向“V”型发展。

河床纵向形态可以用河床比降和凹度两个指标来表示[20]，其中河床比降是一个河段的落差与水平距离的比值，而凹度就是河流纵剖面向下凹的程度。小浪底水库运行后，黄河下游河道出现持续冲刷趋势，河床在冲刷过程，沿程比降变化不大。图4为高村-陶城铺河段汛前河床纵比降沿程变化，2005年的河床平均比降为0.118‰，2016年为0.12‰，这两年河床深泓线凹度值也均接近1，尽管局部河床冲淤调整较大，但凹度值变化不大，表明河床纵剖面在冲刷过程中，以近似于平行下切方式调整，2016年汛前河床高程平均比2005年汛前低约0.92 m。

2.2 边界阻力能耗率响应

2.2.1 沿程水面宽、水深变化 主槽是输水输沙的主要区域，主槽的宽度与深度是体现河道断面形态的主要因子，分析这些断面形态要素的时空变化，可以追溯出不同时期河道地形对边界阻力能耗分布调整的影响。基于一维水动力数学模型，计算出不同流量条件下高村-陶城铺河段各断面的水面宽与水深，分析流量从1000～4000 m3/s变化时沿程水面宽和平均水深的变化趋势。2005年河道地形情况，平均水深从2.53 m增大到4.02 m，增幅58.88%；水面宽从397 m增大到477 m，增幅20.18%。2016年河道地形情况，平均水深从2.32 m 增大到4.30 m，增幅85.28%；平均水面宽从504 m 增大到601 m，增幅19.17%。综上所述，随流量增大，水深变化幅度明显大于水面宽，水深对洪水响应的灵敏度要大于水面宽。

图5和图6分别流量为4000 m3/s条件下水面宽B与水深h沿程分布，B和h沿程呈上下起伏变化，为了更好的分析B和h沿程变化情况，我们采用均方根来判断沿程波动强度：

式中：σ为均方根，表示波动强度；X为沿程水面宽B或水深h变化值，为水面宽B或水深h的沿程平均值。根据式（7）计算出不同流量条件下水面宽B和水深h的波动强度，如表1所列。

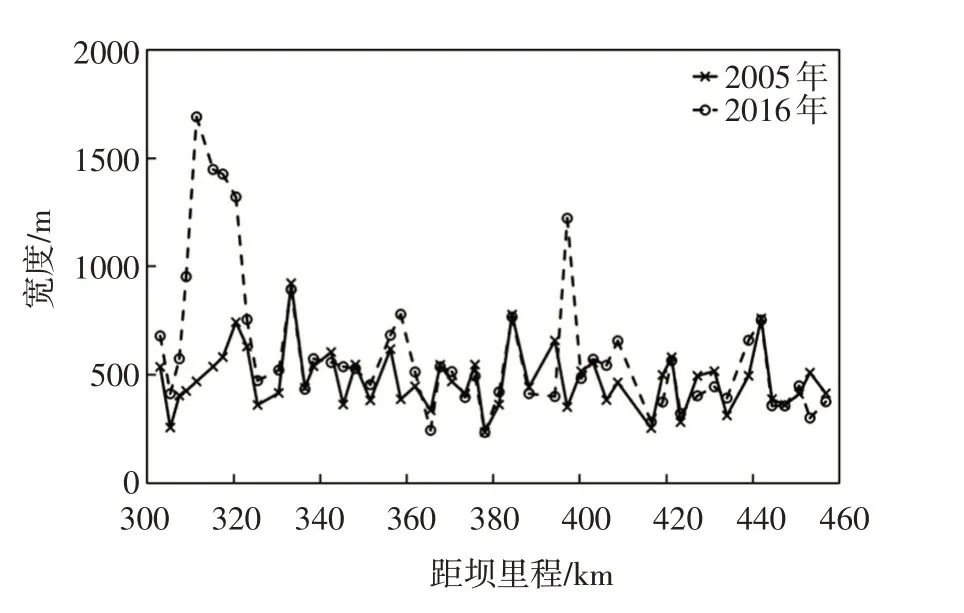
图5 不同时期河宽沿程变化（流量为4000m3/s）

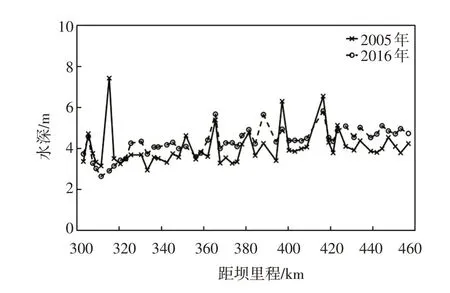
图6 不同时期水深沿程变化（流量为4000m3/s）

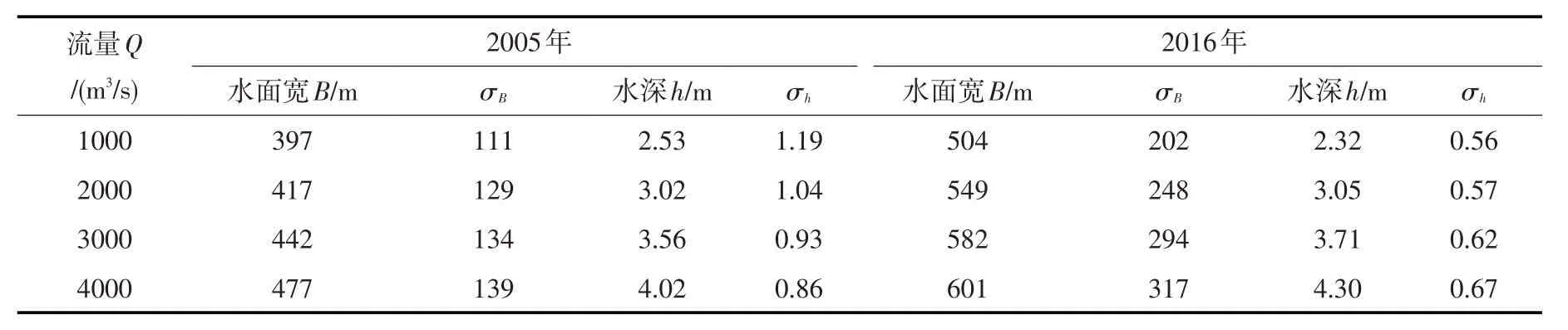
表1 高村-陶城铺河段水面宽、水深沿程均值及波动强度

由表1数据可知，在2005年地形条件下，流量从1000增至4000 m3/s时水深沿程波动强度σh呈减小趋势，减小幅度为28%，而水面宽沿程波动强度σB呈逐渐增大趋势，增大幅度约25%。2016年地形条件下σh随流量增加变化范围较小，基本上维持在0.6左右，但是σB随着流量增加，其增幅高达57%，沿程波动变得强烈。水面宽和水深沿程起伏波动正是边界阻力能耗沿程分配的特性，波动强度越小，说明河道断面形态沿程变化不大，河道趋近相对平衡状态。

2.2.2 沿程边界阻力能耗率 利用一维水动力数学模型计算不同河道地形于不同流量（分别为1000、2000、3000和4000 m3/s）条件下的过水断面、水力半径、比降和平均流速等水力要素，并根据式（6）计算相应的边界阻力能耗率，图7（a）（b）分别为2005年和2016年高村至陶城铺河段的边界阻力能耗率沿程变化情况。

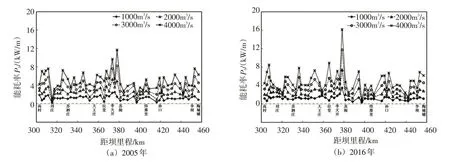
图7 高村-陶城铺河段沿程边界阻力能耗率变化

计算结果表明，随着流量的增大，边界阻力能耗率也随之增加，当流量为1000 m3/s时，单位长度边界阻力能耗率P（b以下简称Pb或阻力能耗率）沿程波动幅度较小，2005年沿程均值为1.26kW/m，2016年Pb为1.25 kW/m；流量为2000m3/s 时，Pb沿程波动幅度有所增大，2005年Pb为2.50kW/m，2016年为2.46 kW/m。当流量进一步增大到3000乃至4000 m3/s时，河槽水流与边界接触面积逐渐增大，Pb波动幅度明显增大，3000m3/s流量时，2005年为3.73 kW/m，2016年为3.67kW/m；流量为4000 m3/s时，2005年为4.99 kW/m，2016年为4.90 kW/m。综上所述，在相同流量条件下，2016年比2005年略小，但是相差不大，说明高村-陶城铺河段的河槽形态经过长达十余年的冲刷调整，除了河床纵比降近似平行下切或少数断面发生较大的形态调整外，其它断面几何形态并没有发生太大的改变，2016年的河道断面形态整体上与2005年比较相似。

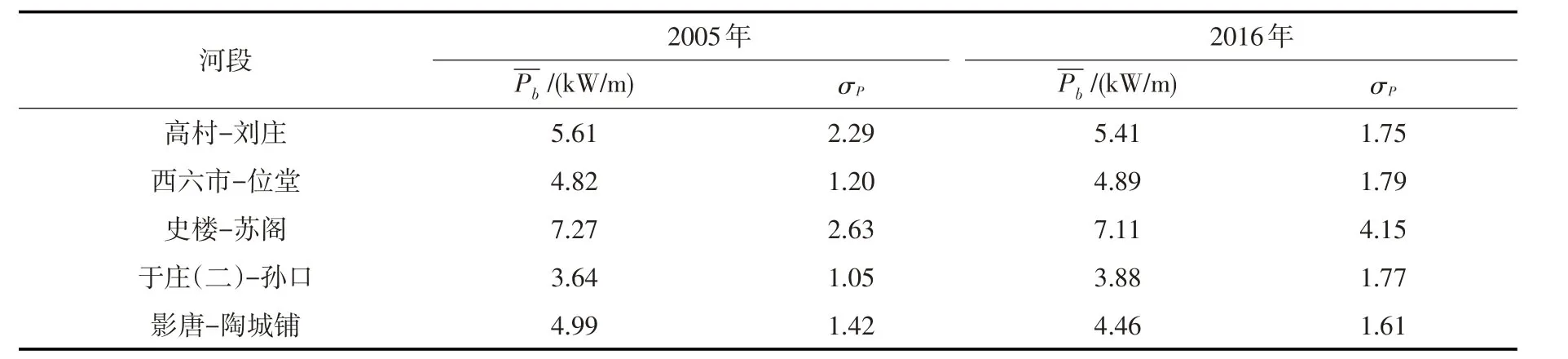
表2 不同河段边界阻力能耗率均值与波动强度（4000m3/s）

同一河道不同河段Pb差距较大，有的河段Pb很大，超过16 kW/m，如徐码头（二）断面；有的河段Pb很小，小到1.03 kW/m，如石菜园断面。本次把高村-陶城铺河段按照Pb沿程变化规律，分为若干个河段进行详细讨论（表2），并绘制成图8，能够清晰直观对比不同河段的均值和波动强度。

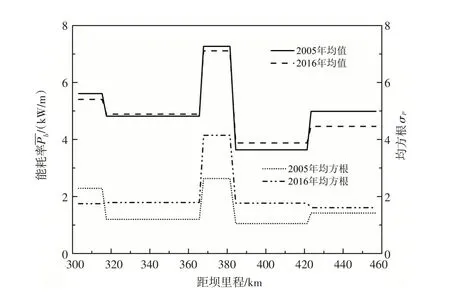
图8 流量为4000m3/s边界阻力能耗率均值与波动强度

3 边界阻力能耗率与断面形态、河床稳定性关系

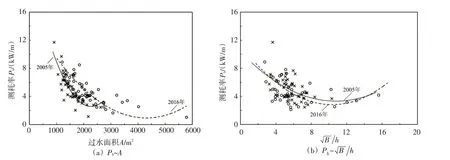
图9 边界阻力能耗率与过水面积、断面形态关系（4000m3/s）

3.1 边界阻力能耗率与断面形态关系水流对河床的塑造是边界阻力能耗长期累积的过程，与河道断面形态密切相关。河槽过水断面面积A、宽深比等形态变量能够反映河道过流能力与断面形态调整趋势，通过分析边界阻力能耗率Pb与A、之间的相关关系（图9（a）（b）），可以追溯河床形态调整的规律。在4000 m3/s流量条件下，Pb首先随着河槽过水面积A或宽深比的增加而减小，达到约束条件下的最小值后随A或的增大呈逐渐增大趋势。从图9（a）可以看出，不同年份的河道地形导致阻力能耗率达到最小值时的过水面积也不一样，2005年Pbmin=2.6 kW/m时，A约为2300 m2，而2016年Pbmin=1.22.6 kW/m 时对应的A约为4200 m2。从图9（b）阻力能耗率Pb与宽深比的关系可以看出，4000 m3/s 流量条件下高村-陶城铺河段的宽深比大多集中在4～8 范围内，2005年河道约为11时，Pb趋向最小，而2016年河道约等于10时，Pb才趋向最小。

上述关系表明，阻力能耗率与断面形态变量之间的关系并不是简单的增减关系，而是呈非线性变化。河道形态变量的调整通常相互作用，相互影响，使得阻力能耗与河槽形态之间关系变得复杂，不同河道断面形态，边界阻力能耗率达到的最小值也不一样。当河道断面形态发生改变，边界阻力能耗也作出相应的调整，反过来又影响断面形态的调整进程，从而导致能耗率最小值很难达到，但是经过不断调整河道断面形态，会逐渐趋向外界约束条件下的最小值。

3.2 边界阻力能耗率与河床稳定性关系冲积河流具有自动调节作用，在一定时段内，流域来水来沙条件和边岸抗冲稳定不变，则河流响应这些条件调整自身空间形态，使河宽、水深、比降及弯道形态等维持一个相应的稳定值，此时称河流处于平衡状态[21]。但是，在天然河流中绝对的、静止的平衡是不存的，往往是以相对平衡（也称动态平衡）的方式存在（图10（a））。

冲积河流的河床是由松散泥沙颗粒所组成，一定条件下会发生冲淤变化，在一定时间间隔，如果所取河段比较长，各地的冲淤变化就可能相互抵消，该河段处于相对平衡状态[22]。某一长河段处于相对平衡状态，局部河床会受到不同程度的扰动，围绕一个平均值不断波动，如果扰动幅度在一定范围内且随时间推进逐渐变小，则该河床处于稳定状态；如果扰动幅度随时间延长逐渐增大，超过了稳定界限，则认为该河床处于不稳定状态（图10（b））。

通过前面计算分析可知，河床边界阻力能耗率围绕均值上下波动（图7），在一定条件下处于相对平衡状态，波动幅度愈小愈趋近平衡状态。当河流处于相对平衡状态，局部河床可能是不稳定的。对于既定的来水来沙和不同形态的断面，河床亦具有不同的稳定性，本次采用河床稳定性指标来说明河床的稳定性，并把边界阻力能耗率与河床稳定性指标进行关联分析。其中，河床稳定性指标[23]如下：

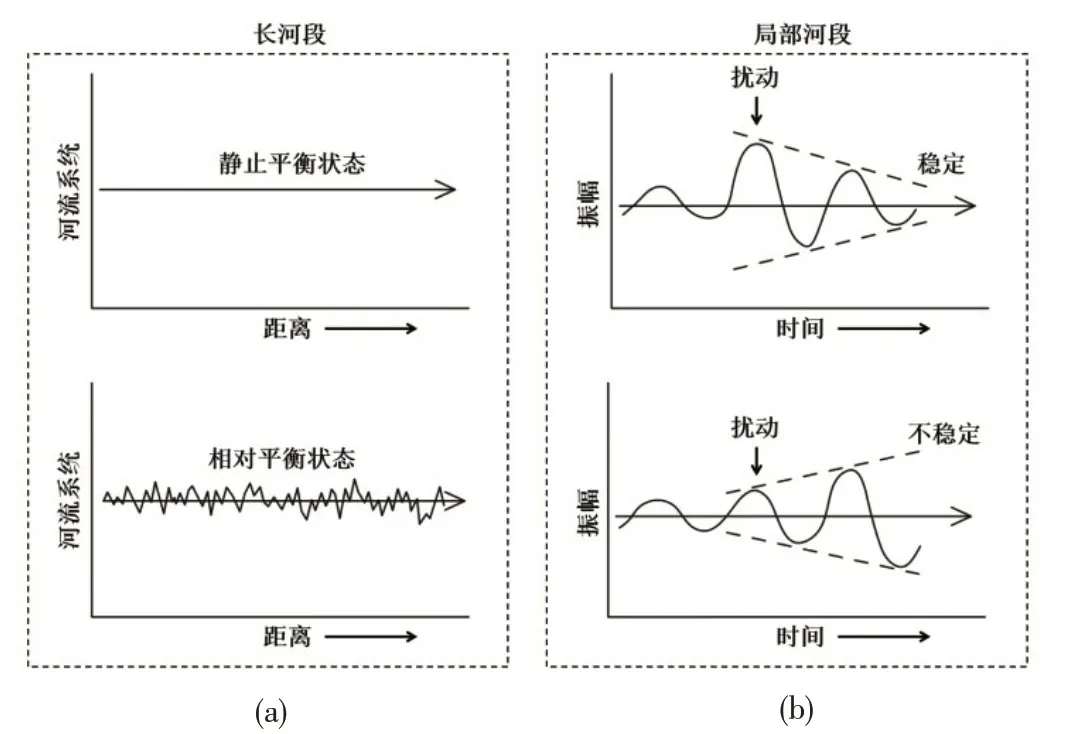
图10 河流系统平衡状态类型与河床稳定性示意

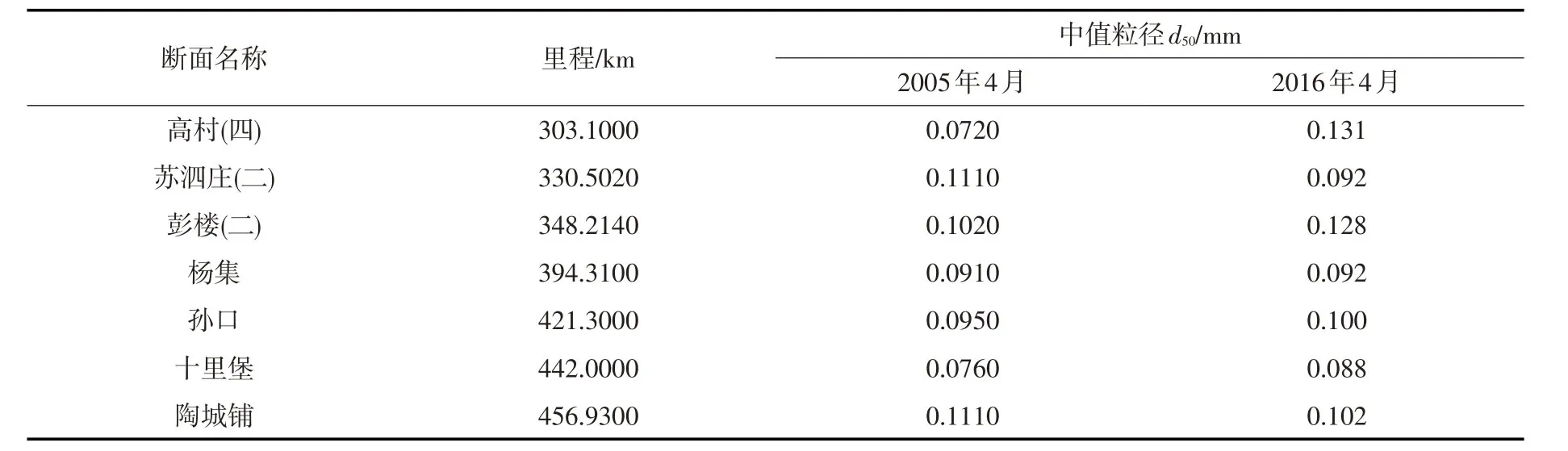
表3 黄河下游高村-陶城铺河段中值粒径变化

式中：τB为床面浑水极限剪切应力；τc为清水床面泥沙起动剪切应力；τb为床面剪切应力。为方便计算，本文采用王尚毅等[24-25]的方法来计算浑水极限剪切应力τB和τb床沙临界剪切应力：

式中：Cm为床面含沙浓度，%；d50为床沙中值粒径，mm；K*为泥沙起动系数，本文取0.062。

表3为黄河下游高村-陶城铺河段部分河段床沙中值粒径。通过计算获得2005年和2016年河床稳定性指标KK与边界阻力能耗率Pb的关系，如图11所示。

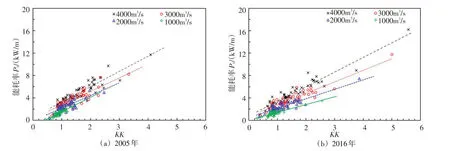
图11 边界阻力能耗率Pb与河床稳定性指标KK关系

从图11可知，边界阻力能耗率与河床稳定性指标呈正相关关系，河床稳定性指标KK值愈大，阻力能耗率Pb也愈大。不过并不是KK值愈大，河床愈不稳定，而是当KK值在一定范围内，河床处于不冲不淤，能够保持稳定状态，当KK值大于或小于这个范围，则河床是不稳定的。王尚毅等[26]提出了河床稳定性条件，并采用黄河花园口和高村共50组数据计算得出，KK值约在0.8≤KK≤1范围内时，河床是稳定的；当KK值大于1，河床处于上限失稳；当KK值小于0.8，河床处于下限失稳。

由计算可知，在流量1000 m3/s 时，KK值多数位于0.8～1.0 范围内，大部分河床处于稳定状态，对应的边界阻力能耗率也相对较小，沿程波动幅度不大，高村-陶城铺河段处于相对平衡状态（图7）。随着流量的增大，河床稳定性指标KK值也随之变大，在流量为4000 m3/s时KK值大于1的数据增多，大部分河床处于上限失稳状态；维持河床稳定的河段也有不少，而这部分河段对应的边界阻力能耗率Pb相对较小，如2005年孙口断面和2016年大寺张断面，其Pb值分别为280 kW/m和293 kW/m。然而，边界阻力能耗率趋向最小值时并不意味河床也处于稳定状态，如1000 m3/s流量条件下边界阻力能耗率趋向最小时，依然存在一些断面的河床稳定性指标小于0.8，处于下限失稳状态。

4 结论

本文利用理论解析、数学模型及实测资料分析相结合的方法，研究黄河下游高村至陶城铺河段的边界阻力能耗率与断面形态、河床稳定之间的关系，主要结论如下：

恒定流量条件下，河床边界阻力能耗率围绕均值上下波动，随着流量逐渐增大其均值和沿程波动强度也越大，河流逐渐远离相对平衡态，反之趋向相对平衡态。河床断面形态的改变引起边界阻力能耗率做出相应的调整，边界阻力能耗率Pb随河床断面形态（过水面积A或宽深比呈先减小后增大的趋势。在流量4000 m3/s条件下，边界阻力能耗率趋向最小值时，2016年汛前河道的过流能力明显高于2005年汛前河道，表现在宽深比有所减小，过水面积更大。

边界阻力能耗率Pb与河床稳定性指标KK具有很好的线性关系，Pb随着KK值减小而减小，但并不是Pb越小，河床稳定性越好，而是当KK处在0.8～1.0之间，河床断面能够维持稳定状态。运用边界阻力能耗率结合河床稳定性指标，通过优化断面设计保持河床稳定条件下使边界阻力能耗率趋向最小，能够提高河道的过流与输沙能力。