多边形内外点判断算法在电力智慧工地中的应用
王迎春,王义春,侯艳权,郭树强,张 帆
(1.国网黑龙江省电力有限公司七台河供电公司,黑龙江 七台河 154600; 2.东北电力大学 计算机学院,吉林 吉林132012)
0 引 言
近年来,电网规模不断扩大,工程安全性问题也成为了重中之重。为了满足日益增长的安全性需求,智慧工地在电网行业得到了广泛的应用。智慧工地即通过物联网技术获取工地中的现场视频等实时数据进行提取分析,以达到降低事故发生概率等目的。其提取处理的内容包括对获取的视频中的人物进行目标检测、越界检测等。越界检测是防止施工现场的工人走出安全区产生危险的一个解决办法,但传统的越界检测中,安全区域一般固定为矩形,不能满足电力工程中复杂的施工环境,难以解决工地中工人走出安全区进入高压危险区域的问题,所以提出将多边形内外点判断算法应用于电网智慧工地中的越界检测,将多边形作为安全区域的边界,通过目标检测确认目标工人的一点,通过该点是否在多边形内部的判断实现工人是否越界的判断,完成安全区域内工人的越界检测,提高电力施工的安全性。
判断目标点是否在多边形内是计算机视觉中的传统问题,主要应用于地理信息系统等方面。该问题自提出后,得到了众多学者的关注。目前主要有文献[1-2]提出的射线法、文献[3]提出的夹角之和检验法、文献[4]提出的面积和法等,这些算法虽过程简单、空间复杂度较低,但是算法的时间复杂度较高,应用到实际项目中时耗时严重。因此,在二叉空间分隔(Binary Space Partitioning, BSP)树的基础上进行多边形内外点判断算法的改进,提高判断速度以应用于实际问题中。
1 传统多边形内外点判断算法
1.1 射线法
射线法是最早提出的多边形内外点判断算法,判断过程如下[5]:
1)判断目标点A(x0,y0)与多边形的顶点P(xi,yi),(i=1,2,...,n)是否相同或目标点是否在多边形的边上,若都不在则进行下一步。
2)计算|y0-yi|的最小非0值,记为my;计算|x0-xi|的最大值,记为Mx。
3)由目标点引出1条射线,为了避免射线与多边形顶点相交,将射线斜率定为my/2Mx。所以射线参数方程为R=(x0,y0)+k(2Mx,my),(0 4)将应用射线法将判断点与多边形的关系转换为判断该射线和多边形的边的交点数。计算交点数需计算D1(D-D1)>0和D2(D-D2)>0,其中: 5)算出交点个数,若为奇数则点在多边形内,若为偶数则点在多边形外。 1.2.1 BSP树的原理和构建 BSP树是一种空间分割树,它主要用于游戏中的场景管理,尤其是室内场景的管理。它的本质是二叉树,也就是用一个面把空间分割成两部分,分割出的空间则继续用面分割,以此类推,直到达到特定递归深度,或者空间中不再有物体或只剩下1个物体。 应用于二维空间的BSP的基本原理是将所有平面建成一棵树,每个平面都将它所在的空间分为2个部分,空间位于平面的前后位置决定了代表空间的节点在树中的位置。 传统基于BSP树进行点在多边形内外判断的算法将BSP树应用于二维空间进行分区[6]:假设给出平面P及直线方程ax+by+c=0,该直线穿过平面并将平面分成两个部分,直线的法向量n(a,b)指向的一侧为正,而另一侧为负。用BSP树来表示分区结果:树中的每1个节点表示1条分割平面的直线,节点的左子树表示正侧,右子树表示负侧;每1个分割的区域都可以由另外的直线再次分割,递归下去最后得到的区域由树的叶子节点表示。如图1的多边形分区后由图2的二叉树表示,多边形中a代表分区直线,p代表所分区域。 图1 多边形分区结果 图2 BSP树表示结果 1.2.2 算法流程 传统基于BSP树的多边形内外点判断算法的流程如下所述: 1)给定1个任意的简单多边形,根据多边形的具体形状以及顶点坐标进行垂直分解,形成多条垂直扫描线,每2条扫描线形成1个垂直区域并结合BSP树构建的方法构建1颗BSP树以表示这些垂直区域。 2)利用多边形的边作为划分直线,基于划分直线两边的区域个数构成1棵与多边形的边有关的BSP树。 3)在判断目标点是否在给定的多边形中时,用建好的垂直区域部分的BSP树查找目标点所在的垂直范围,如果查找到,利用边部分的BSP树确定目标节点所在的具体区域,从而可以判断出目标点是否在多边形内部。 传统算法的时间复杂度不稳定,当BSP树的每个节点只有左子树或右子树时,树结构会退化为链表,时间复杂度会上升。 为了防止BSP树退化为链表,首先对多边形各个顶点的横坐标值进行归并排序,其次用二分法遍历已经有序顶点的垂直直线,最后建立垂直区域的BSP树。经过排序再遍历可以使最后形成的BSP树为平衡二叉树,不会退化为链表,具体流程如下。 1)假定给出任意的简单多边形Q,如图3所示。 图3 简单多边形Q 2)根据多边形的最大及最小坐标值,建立多边形的外包围盒,如图4所示。 3)对多边形Q的各个顶点的横坐标值进行归并排序并用二分法对有序的竖直直线进行遍历,构建垂直区域的平衡二叉树。由于使用二分法进行遍历,所以从边a7开始处理。a7的x1将多边形划分为2个区域,而a7的x2将其中1个区域又划分为2个部分,如图5所示。 图4 简单多边形的外包围盒 图5 被x1与x2分割后的包围盒 4)划分完1个垂直区域后,将这个区域之中的多边形的边插入,使得1个区域被划分为若干个梯形区域。如图6所示,划分完垂直区域后,生成垂直区域的BSP树,再将边a7插入,即将a7按其所对应的区域插入BSP树中。 图6 插入边a7的结果 5)对于余下各边,均采取同样的方式进行处理,将每一个垂直区域和垂直区域内的若干梯形区域都使用BSP树进行管理,多边形的处理结果如图7所示,所构建的二叉树如图8所示。 6)构建好二叉树后,判断点和多边形的关系,首先在垂直区域的BSP树查找目标点所在的垂直区域,确定了垂直区域后,再查找相应边的BSP树,最后确定点是否在多边形内部。 图7 插入所有边的结果 图8 改进算法后构建的二叉查找树 算法的输入为任意简单多边形,输出为判断点是否在多边形内的结果,具体步骤如下: 1)读入离散点和多边形; 2)构造多边形的外包围盒; 3)对多边形的端点横坐标值排序; 4)用二分法遍历排序后端点的垂直分割线,构建垂直区域的BSP树; 5)遍历多边形的边,将边插入到对应垂直区域的BSP树中,生成与边有关的BSP树; 6)在BSP树中查找目标点并给出结果。 当要查询的目标点正好位于划分直线上,即多边形的边上时,将该点进行单独处理。将该点分别左移、右移一小段距离,两次移动后分别对移动后的点是否在多边形内再次进行判断。若两次结果都在多边形内(外)部,则说明移动前该点在多边形内(外)部;若两次结果不一致,则采用其他方法进行判别。 所提算法在研究点是否在多边形内时,分为创建BSP树和查找两个阶段。在创建BSP树时,对多边形各个顶点的横坐标值进行排序,由于使用的是归并排序,所以时间复杂度为O(nlgn);创建多边形对应的BSP树的时间复杂度为O(nlgn);所以,创建BSP树的时间复杂度是O(nlgn)。创建完成后,对点是否在多边形内部进行判断,在垂直区域的BSP树中查找目标点所在的垂直区域,由于排序之后是平衡二叉树,所以时间复杂度为O(lgn);确定点属于的垂直区域后,对确定的垂直区域对应的边的BSP树进行查找,假定每个垂直区域包含m条边(一般m 将算法应用到电力智慧工地中时,根据应用场景的实际情况,选择在能拍到目的区域的点处安装摄像头,并提前对摄像头能拍摄到的区域图像做划分处理,用坐标的方法在图像中划分出安全区。以图9场景为例进行越界检测,画线区域内部为安全区,画线外部为危险区域。 图9 越界检测实验场景 在对工人的目标检测方面,首先,把VGG16卷积神经网络模型在ImageNet数据集上进行参数初始化;其次,在CVC行人数据库的数据集(数据集地址:http://www.cvc.uab.es/adas/site/?q=node/7)上训练基于VGG16的SSD检测模型;最后,在摄像头传输的视频中,每秒抽取24帧图像作为检测图像,对工人进行目标检测。将检测结果返回回归框的左上角和右下角的坐标点,提取回归框下边界的中心点,再进一步利用改进多边形内外点判断算法判断工人是否越过安全区。 射线法、传统多边形内外点判断算法与改进多边形内外点判断算法的时间对比结果如表1所示,表中数据为各个算法的相对运行时间。根据表1可知,改进多边形内外点判断算法的判断速度更快。将改进多边形内外点判断算法应用于电力智慧工地中进行工人是否越过安全区的判断,试验结果表明,该算法能有效地解决工人越界问题,使电力智慧工地中的安全区域划分更加精准,并提高施工安全性。 表1 不同算法的判断时间对比Table 1 Comparison of judgment time under different algorithms ms 对改进多边形内外点判断算法进行阐述,并将改进算法与传统算法等进行对比实验,比较判断时间后给出实验结果,结果表明改进算法比传统算法的判断速度快。同时,将改进算法应用到电力工程领域,用于实际的行人越界检测,检测结果表明该算法可以有效判断行人是否跨出安全区,提高了电力工程的安全性,有较大的实用价值。1.2 传统基于BSP树的多边形内外点判断算法
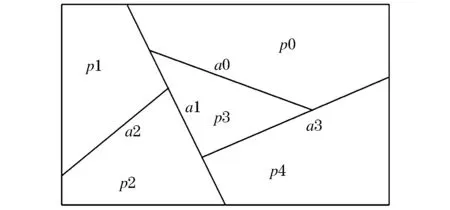
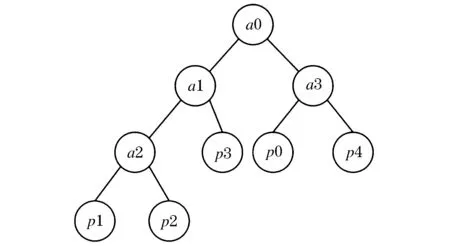
2 多边形内外点判断算法的改进及应用
2.1 改进多边形内外点判断算法的流程



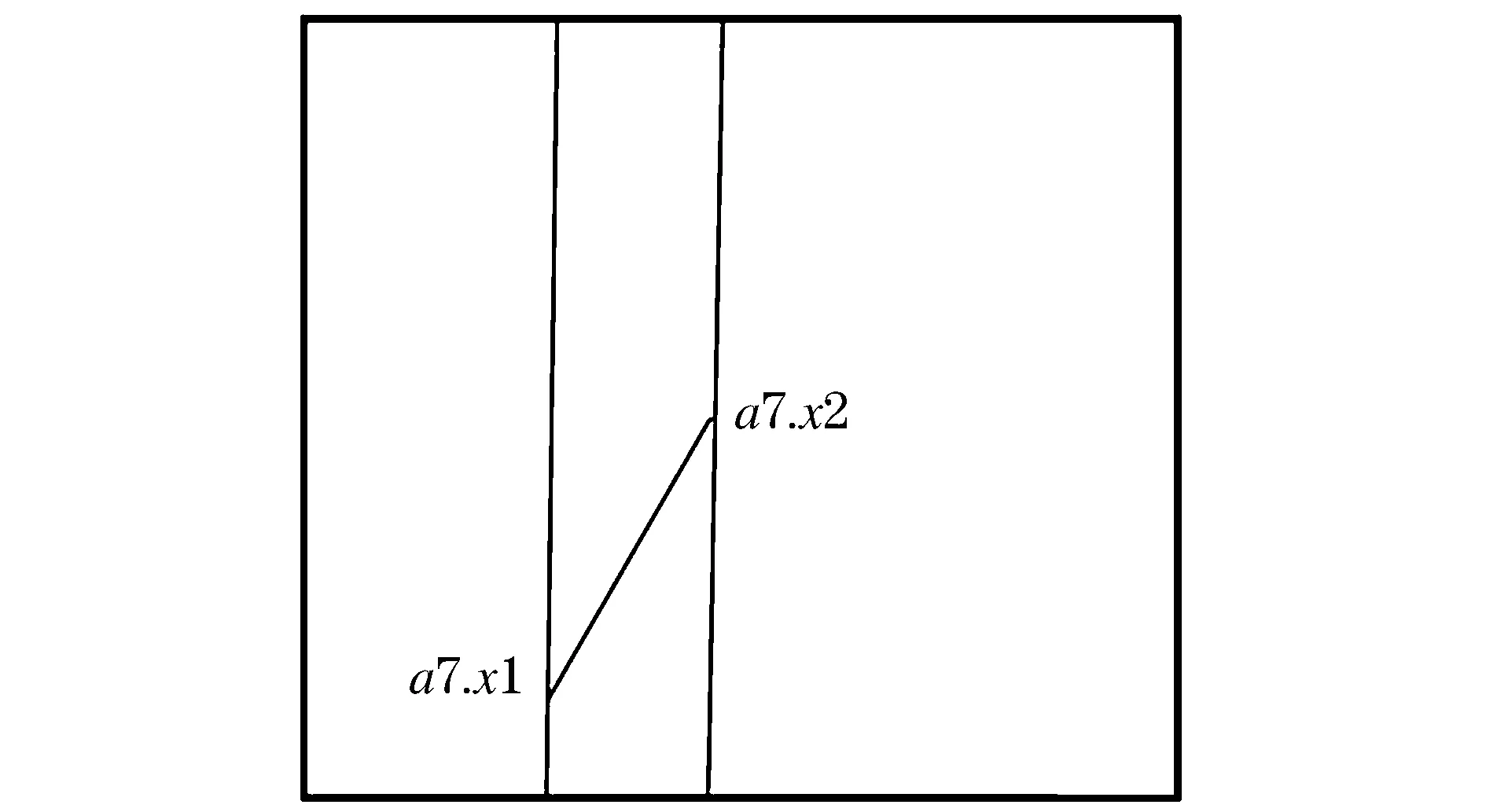
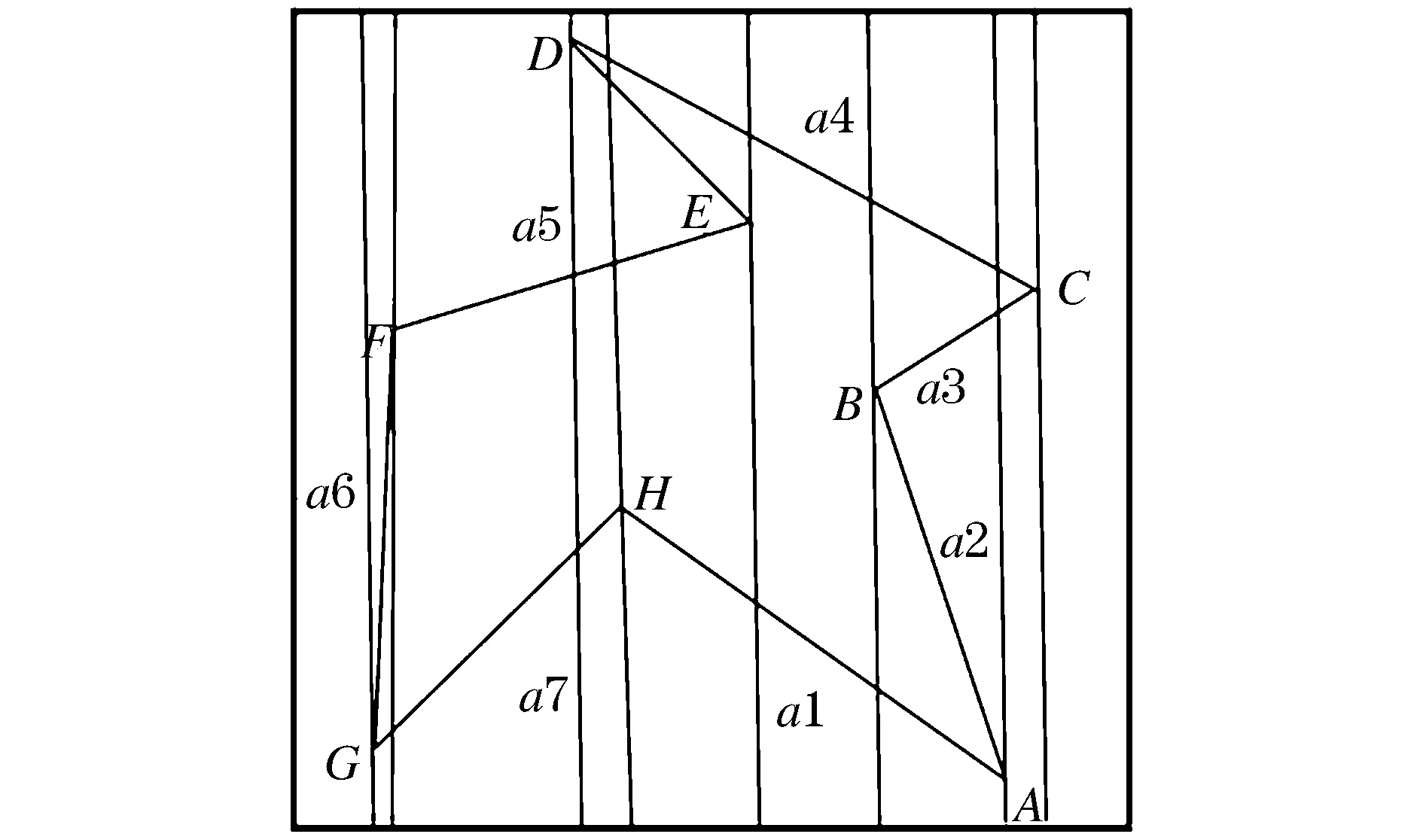

2.2 改进多边形内外点判断算法的实现
2.3 算法的特殊情况
2.4 算法的实验结果及应用


3 结 语

