基于小波能量谱分析的变压器振动特性
李少飞,马兴明,毛新宇
(国网黑龙江省电力有限公司大庆供电公司,黑龙江 大庆 163000)
0 引 言
电力变压器作为电力系统的关键设备,也是最为昂贵、复杂的设备之一。由于电力变压器处于电网的中心位置,运行环境复杂,且时常遭受各种不良运行工况的冲击,一旦发生故障,极有可能造成突发大面积停电,甚至引起爆炸、火灾等事故,带来较大的直接和间接经济损失[1-3]。因此对变压器的运行状况进行长期监测,及时评估变压器状态,能够有效减少突发故障带来的损失。
变压器振动信号能够有效反映变压器的运行状况及内部状态[4-6],因此对变压器振动问题的研究及对振动信号的分析是目前的研究热点。文献[5]利用变压器振动测试系统,对在变压器油箱表面测得的铁芯及绕组的振动信号进行研究,在理论研究影响铁芯及绕组振动各因素的基础上,实验验证了在空载状态下油箱表面测得的铁芯振动信号的基频幅值与施加电压的平方以及绕组振动信号的基频幅值与流过绕组的负载电流平方都呈较好的线性关系。文献[6]基于变压器铁芯及绕组噪声及振动机理,建立振动噪声测量系统,测量变压器实际振动及噪声信息,根据指纹成像噪声源定位和振动信号特征值测试结果,对变压器内部故障进行定位。文献[7]针对变压器绕组多种故障并发的工况,在分析变压器绕组振动机理的基础上,提出一种基于集合经验模式分解的振动信号提取方法,对变压器绕组振动信号进行分解得到各阶本征模函数并构造特征矢量,将该特征矢量作为变压器绕组状态识别的判据。以上研究对变压器振动问题进行了相关的建模与理论分析,但是对于变压器长期带电运行下的振动监测未进行相关的研究。
本文针对变压器稳态运行振动问题,建立变压器振动分析原理及模型,测量变压器带电运行状态下箱体不同位置的振动信号,基于小波分解原理对振动信号进行分解重构及能量谱提取,实现对变压器振动的辨识及内部状态的诊断。
1 变压器振动机理
变压器振动主要由变压器本体(铁芯、绕组)的振动和冷却装置的振动通过机械连接及绝缘油传递到变压器表面。在变压器箱体表面可采集到的各种振动信号中,油泵、风扇等冷却装置的振动频率与铁芯、绕组振动有明显区别,易于分离[8-9]。因此,分析变压器箱体表面振动信号可得,振动信号主要是由变压器本体产生的。
1.1 铁芯振动机理
铁芯振动主要原因是硅钢片的磁致伸缩[10-11]。根据电磁感应原理及铁磁材料磁致伸缩特性,可得铁芯磁致伸缩引起的振动加速度a1为
式中:L为铁磁材料原始尺寸;εs为硅钢片的饱和磁致伸缩率;Us为电源电压幅值;N为一次侧绕组匝数;S为铁芯横截面积;Bs为铁芯饱和磁感应强度;ω激励频率。
振动加速度在材料及运行条件不变的情况下与电压平方呈正比关系,振动频率为激励频率的2倍。变压器正常运行时,激励为工频激励,因此铁芯振动的基频为100 Hz,但是受到铁磁材料的非线性及铁芯内框和外框的磁通路径长短不同的影响,使得铁芯内出现以100 Hz为基频的高次谐波。
1.2 绕组振动机理
处于磁场中的载流导体要承受机械力的作用,当变压器绕组中通过电流时,由于电流与漏磁场的作用,在绕组内产生电磁机械力,其大小由通过绕组的电流与漏磁场的磁通密度大小共同决定[12-13]。作用在绕组线圈上的电动力F为
式中:p为电动力系数;Im为负载电流幅值;φ0为负载电流初相位。
根据变压器绕组的机械结构,常将变压器绕组等效为弹簧质量系统,根据动力学定理可得绕组振动加速度由一个稳态分量及逐渐衰减的分量组成,在理想状态下稳定运行的变压器绕组的振动加速度信号是电源频率的2倍,对于工频网络即为100 Hz。振动加速度大小正比于绕组电流的平方。而由于加速度受绝缘材料弹性系数影响,绝缘材料弹性系数不是常数,具有较强的非线性特性,导致绕组振动在负载较大时呈明显的非线性特征且出现较多的高次谐波。
2 小波变换原理
目前针对变压器振动信号的分析多采用快速傅里叶变换(Fast Fourier Transform, FFT),相比快速傅立叶变换而言,小波变换(Wavelet Transform, WT)本质上是一种窗口大小固定不变而其时频窗可以改变的时频局部化分析方法,在高频部分具有较高的时间分辨率和较低的频率分辨率,在低频部分具有较高的频率分辨率和较低的时间分辨率[14-15],小波变换原理图如图1所示。
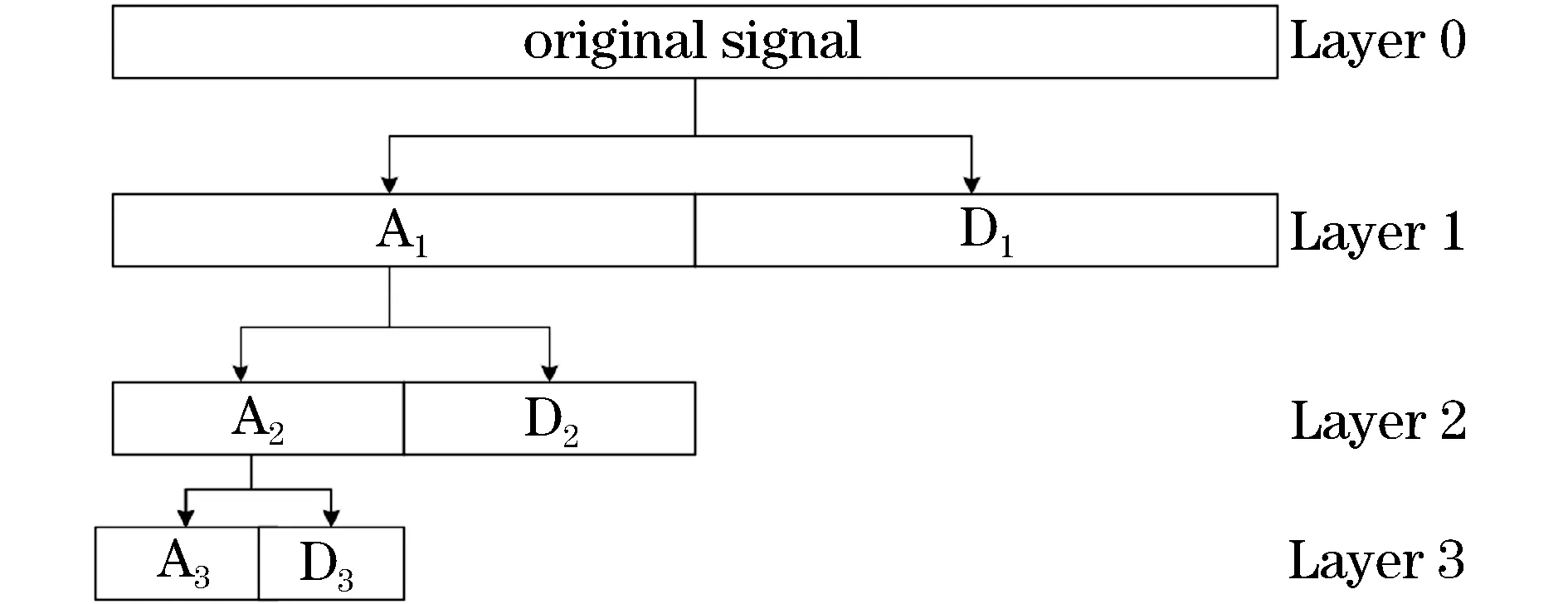
图1 小波变换原理图
正是因为WT具有可变精度特性,从而使其既有足够的时间分辨率对信号中的短时高频成分进行分析,又有良好的频率分辨率对信号中的低频信号进行分析。对于非平稳信号的分析,WT有着FFT难以替代的优势。WT的基本思想同FFT相似,均为采用一族函数来表示一个信号或函数。不同的是FFT变换时将一连续的、平稳的时域信号表示为不同频率的正弦函数的线性叠加,而WT则是通过对基波函数的伸缩和平移来构成的。
对于能量有限信号,满足
其小波变换定义为以函数簇ψa,b(t)为积分核的积分变换,如下式:
式中:a为伸缩因子;b为平移因子;a-0.5为归一化常数,用来保证变换的能量守恒。
函数簇ψa,b(t)为小基波函数ψ(t)经过伸缩和平移产生的小波函数簇:
变换前后,信号能量守恒,即
由上式可以看出,WT是一种线性变换,物理含义就是用一簇频率不同的震荡函数ψa,b(t)作为窗口函数对信号x(t)进行扫描和平移,此时WT在某种意义上类似于FFT变换;但不同的是,WT的时域和频域分辨率与频率有关,在高频段,小波变换能达到高时域分辨率,而频域分辨率交叉,在低频段时相反,这是快速傅里叶变换不具备的。
3 振动信号故障分析
变压器的振动信号频率成分十分丰富,适宜采用WT分析振动信号。因为FFT仅得到频域上一些离散频点的信息,会导致离散频点外的信息丢失,而小波变换的结果是表征各个频段的时域信息,且时频窗口大小随尺度变化,可实现对低频信号采用大时窗、对高频信号采用小时窗的分析要求。利用小波理论对变压器的振动信号进行多分辨率分析,并对各个频段能量进行量化处理,可提取出振动信号的频段-能量对应关系,作为变压器故障诊断的依据。变压器正常运行时,其能量大部分集中在100~300 Hz内[16-17],当变压器发生故障或存在潜在故障时,高频成分增加,导致高频能量比例增大、主频段能量减小。将正常运行状态下的各频段能量作为参考指纹向量,用实时监测到的数据同此参考指纹量作比较,当主频段能量小于某一特定值或高频(>600 Hz)分量能量高于某一特定值时,诊断为变压器故障。当然,此特征值的具体数值,因变压器的类型、容量而异,需要通过试验并结合现场运行经验来确定。
采用JF2001-T压电式加速度传感器以及NI9234数据采集仪对1台型号为S11-M-10/10的变压器样机进行振动测试,采样频率为2 kHz。测试接线原理图如图2所示。
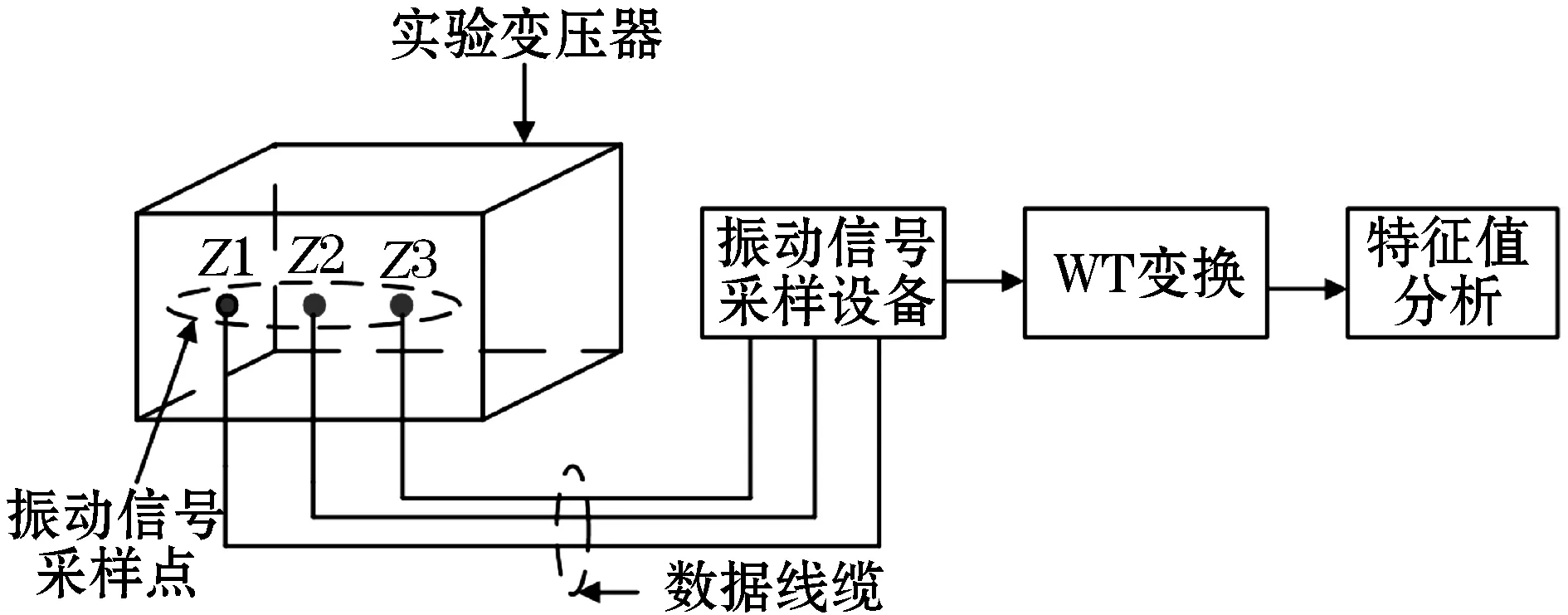
图2 测试接线示意图
对变压器箱体不同位置的振动信号进行采样,将采样数据经由振动信号采样设备进行模数转换,对转换后的数字信号进行WT变换。振动原始信号如图3所示。
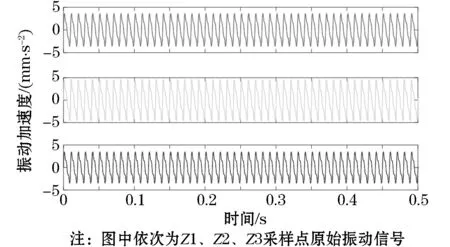
图3 原始振动信号
由图3可知,变压器振动信号具有明显的周期性,但由于振动信号为较多周期信号的叠加,因此仅依靠原始振动信号幅值变化很难对振动信号进行有效识别。对原始振动信号进行FFT变化,得到振动信号频域结果,如图4所示。
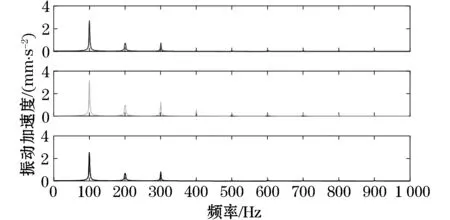
图4 FFT变换结果图
不难看出,变压器正常运行时,绕组振动信号集中于100 Hz,并含有少量以100 Hz为基频的的高次谐波,但由于FFT变换无法区分振动信号的时域差别,会导致对变压器运行的错误判断,因此对Z2采样信号采用db9小波进行4层分解重构,并提取重构信号能量谱,得到如图5所示结果。
由图5(b)可知,第4层的高频分量d4与原始信号的总趋势相吻合,无需再进行下一层的小波分解,第4层对应于0~250 Hz频段;其低频分量a4(对应于0~100 Hz)幅度较小,可见振动信号的主频段为100~200 Hz。
由图5(a)可知,每进行1次小波分解,对应的低、高通滤波器实际频带减半,即实现2分频,经过4层分解后,其相应的低、高频能量占比分别为EL、EH,1-4层能量占比分别为17.32%、7.21%、11.26%、64.21%。由此可见第4层(0~250 Hz)分解重构信号能量占比较大,第4层EH约为61.69,说明变压器振动信号主要集中于100~200 Hz,而第3层(250~500 Hz)分解重构信号能量占比约为11.26%,表明变压器中频振动信号占比仍较大,对于第1、2层分解重构信号,其能量占比受到外界环境以及测量误差的影响,其能量谱结果对基于振动信号监测的变压器运行状态来说意义较小,因此可以采用第4层分解重构结果作为变压器振动信号指纹量,以监测变压器运行状态并对变压器运行状态进行快速有效的诊断。进一步研究变压器不同故障下能量谱变化,得到如表1所示结果。

图5 小波变换结果
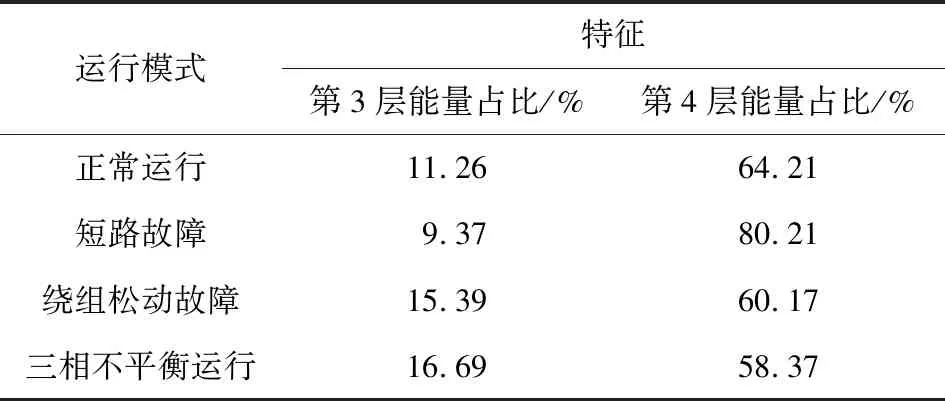
表1 不同运行状态能量谱特征
由表1可以看出,当变压器发生故障时,变压器振动小波分解重构信号能量谱变化较为明显,以4层小波分解第3、4层分解重构信号能量占比为指纹量进行分析可以看出:
1)短路故障下低频信号能量占比增加24.91%,中频信号能量占比下降16.78%。分析其原因,当变压器短路时,工频电流激增,使得100 Hz分量下振动加速度明显增加,使第4层分解重构信号能量占比增加。绕组松动故障下低频信号能量占比下降6.29%,中频信号能量占比下降36.67%。分析其原因,当变压器绕组松动故障时,振动加速度高次谐波增加,使得低频信号能量占比下降。三相不平衡运行故障下绕组振动加速度能量占比变化情况与绕组松动故障基本一致,其原因也是受到不平衡运行谐波的影响,使得低频信号能量占比下降。
2)通过对振动信号的分解重构及能量占比特征值的提取,能够较好地判断变压器的运行故障,并及时制定解决措施。
4 结 语
1)变压器正常运行时,100~200 Hz振动信号分量能量占比较高,且包含以100 Hz为基频的中高频振动信号,当变压器故障时,不同频率信号分量能量占比变化。
2)基于小波分解重构的振动信号能量谱能够有效识别变压器运行故障及内部结构问题,为基于振动信号分析的变压器故障诊断问题提供了辅助决策。

