基于模态柔度的高桩码头桩基损伤识别*
王启明,朱瑞虎,王 宁,罗梦岩,车宇飞
(1.河海大学 理学院,江苏 南京 210098;2.河海大学 港口海岸与近海工程学院,江苏 南京 210098)
我国大部分高桩码头建于20世纪,在数十年的运营期内很多桩基因腐蚀、疲劳、撞击等原因发生了损伤,部分结构损伤还相当严重,这些损伤如不能及时被检测维修,将会造成灾难性的人员伤亡和财产损失。目前桩基检测方法主要包括高应变检测法、低应变检测法和局部检测法(超声波法、电磁雷达法等)[1-2],由于高桩码头桩顶嵌固、桩身大部分位于水面以下等因素制约,上述方法不能实现高桩码头桩基的无损、快速检测。
基于动力指纹的损伤识别方法综合运用了结构振动理论、振动测试和数字信号处理等跨学科技术,具有无损、快速检测的优点,很多学者已开展动力指纹损伤识别在高桩码头桩基健康检测、监测中的应用。孙熙平[3]通过数值仿真与物理模型试验研究高桩码头结构的振动模态,并用模态应变能变化率作为损伤诊断指标诊断出码头桩基损伤;张干[4]以残余力向量绝对值作为诊断指标,对髙桩码头桩基损伤进行诊断;朱瑞虎[5]通过数值模拟计算,证明曲率模态能敏感反映高桩码头桩基损伤位置,并采用概率灵敏度分析方法研究了高桩码头桩基损伤与码头整体动力特性的关系。但模态柔度在高桩码头桩基损伤识别中的研究鲜见报道,本文设计了高桩码头动力损伤研究模型,通过有限元数值模拟与动力试验研究模态柔度在高桩码头桩基损伤识别中的适用性。
1 模态柔度指纹
由结构动力分析理论可知,结构柔度矩阵用模态参数表达为:
(1)
式中:F为结构柔度矩阵;ωi表示第i阶固有振动频率;φi为第i阶频率下对质量归一的振型向量;n为结构自由度。
(2)
式中:Ui为每个节点ULS值;fi,j为该节点所在一致荷载面中柔度矩阵的元素;m为结构节点数。
利用式(1)、(2)计算损伤前后的模态柔度,记未损伤柔度矩阵、模态柔度分别为:
(3)
损伤后柔度矩阵、模态柔度分别为:
(4)
每个节点损伤前后模态柔度的差值为:
(5)
2 基于有限元模拟的模态柔度损伤识别
2.1 有限元模型建立
数值仿真和动力试验采用同一高桩码头模型,该模型长2.05 m、宽0.90 m、高1.65 m,共3跨,排架间距0.65 m。码头前沿和中间为单直桩,后方为一对叉桩,采用直径0.06 m、壁厚2 mm的钢管模拟,直桩两端分别伸入桩帽和底部固定结构,中间自由桩身长度为1.3 m,码头上部横梁、纵梁、面板均采用混凝土浇筑。本文重点研究泥面以上部分桩身的模态柔度损伤识别,考虑实际工程中桩身固结深度下方实际位移为0,将桩固结点上部土体约束简化为10 cm混凝土约束、混凝土及桩基底部均完全固结[8]。
根据模型设计情况进行有限元数值模拟,有限元建模参数如下:混凝土密度为1 950 kgm3,弹性模量为36 GPa,泊松比为0.2;钢管桩密度为7 850 kgm3,弹性模量为210 GPa,泊松比为0.3。所有构件均采用C3D8R实体单元模拟,该单元为三维八节点空间体,具体划分时根据各构件特点选择不同大小和形状,有限元模型共计2 606个单元,不同构件接触面之间完全耦合,有限元网格划分及前排桩编号见图1,前排从右至左分别为1号桩~4号桩。

图1 有限元网格划分及前排桩基编号
2.2 损伤工况模拟
为研究桩基损伤情况下高桩码头动力特性变化情况,分别在码头模型前排2号、3号桩身模拟损伤情况,2号、3号桩基混凝土面以上桩帽以下长度为1.3 m,将其平均分成13段,每段长度为0.1 m,桩身分段及节点编号见图2。损伤位置设置在2号桩5号段和3号桩19号段,损伤程度分别设置为5%、10%、20%、30%,损伤通过减小结构段刚度实现。


图2 桩结构分段及节点位置
2.3 动力特性计算分析
通过有限元模拟,对码头模型计算模态分析可得各工况下的频率和振型,由于柔度矩阵主要由低阶模态决定,本文通过码头模型前两阶振型近似计算2号桩和3号桩的柔度矩阵。由式(1)可以看出:参与计算的模态阶数越多,模态柔度的计算值越收敛于精确值。由于模态柔度与频率平方的倒数成正比,模态柔度识别结构低频模态的变化最为敏感。因此在大型工程结构中往往采用低阶模态参与计算。由于篇幅所限,仅列出完好工况下的模态情况。完好工况下码头模型的一、二阶频率分别为10.35、32.22 Hz,前两阶频率对应的振型见图3,可以看出高桩码头模型一阶振型主要为沿码头纵向摆动,二阶振型主要为沿码头横向摆动。

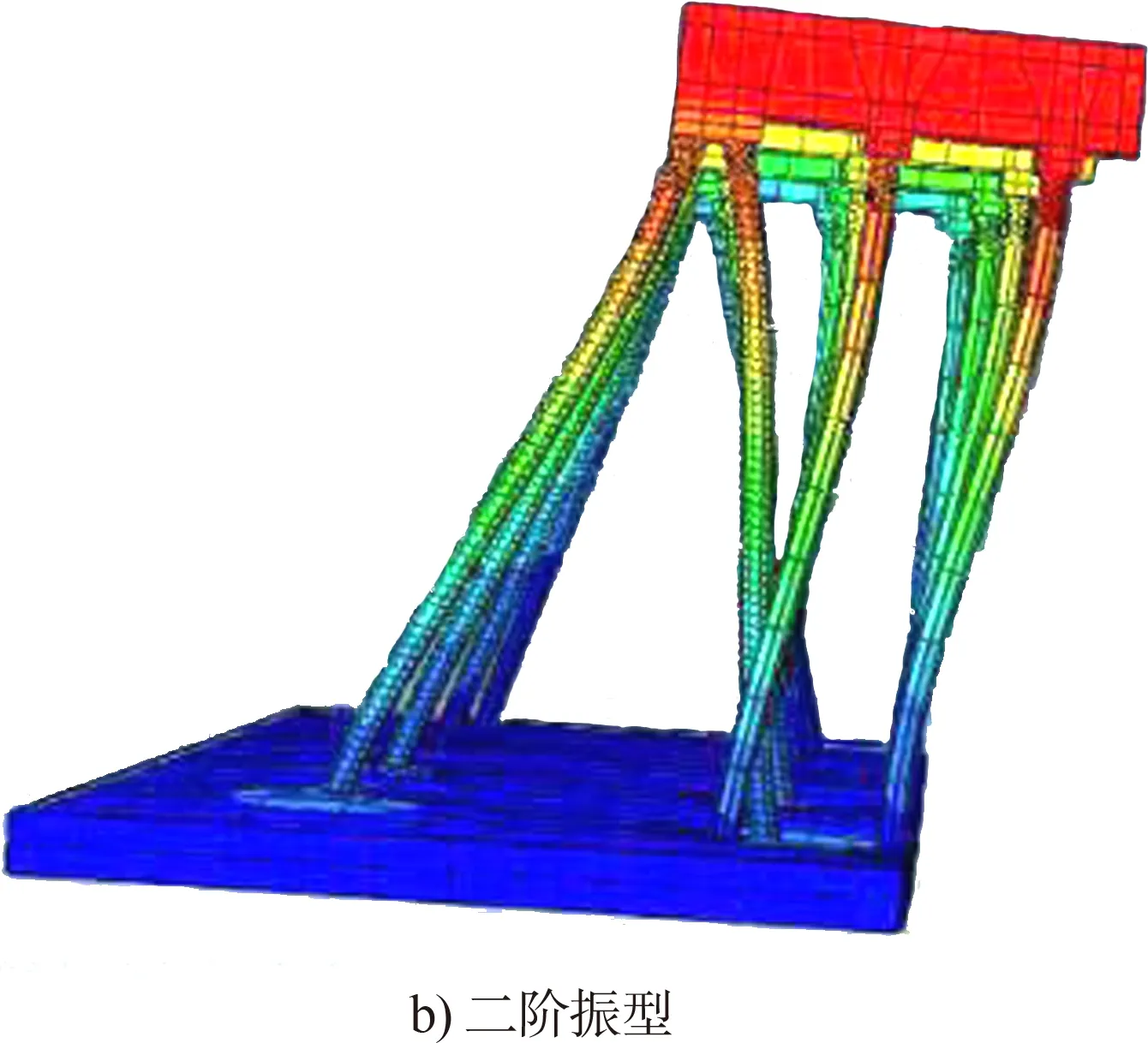
图3 高桩码头模型振型
2.4 数值模拟伤识别结果
将完好工况的前两阶频率值及振型值代入式(3),计算完好工况下各节点模态柔度;将各损伤工况下的前两阶频率值及振型值代入式(4),计算完好工况下各节点模态柔度;通过式(5)计算4个工况下的模态柔度差,结果见图4。从图4可以看出:模态柔度较好地识别了桩基的损伤位置,变化量在损伤位置有“尖峰”出现。模态柔度横坐标为节点编号,5号、6号节点为2号桩5号段的两个端点,2号桩5号段损伤时5号节点模态柔度变化量最大,6号节点次之,这是由于5号节点主振型振幅比6号节点大,因此在损伤后5号节点的振型变化量及其衍生出来的模态柔度变化量大于6号节点,由5号节点和6号节点为所有节点中模态柔度变换量最大节点,可判断2号桩基5号段损伤;同样,19号、20号节点为3号桩第19段的两个端点,根据模态柔度变化情况可判断19号段损伤;还可以看出损伤程度越大模态柔度变化量越大,模态柔度变化量可定性反映结构损伤程度。
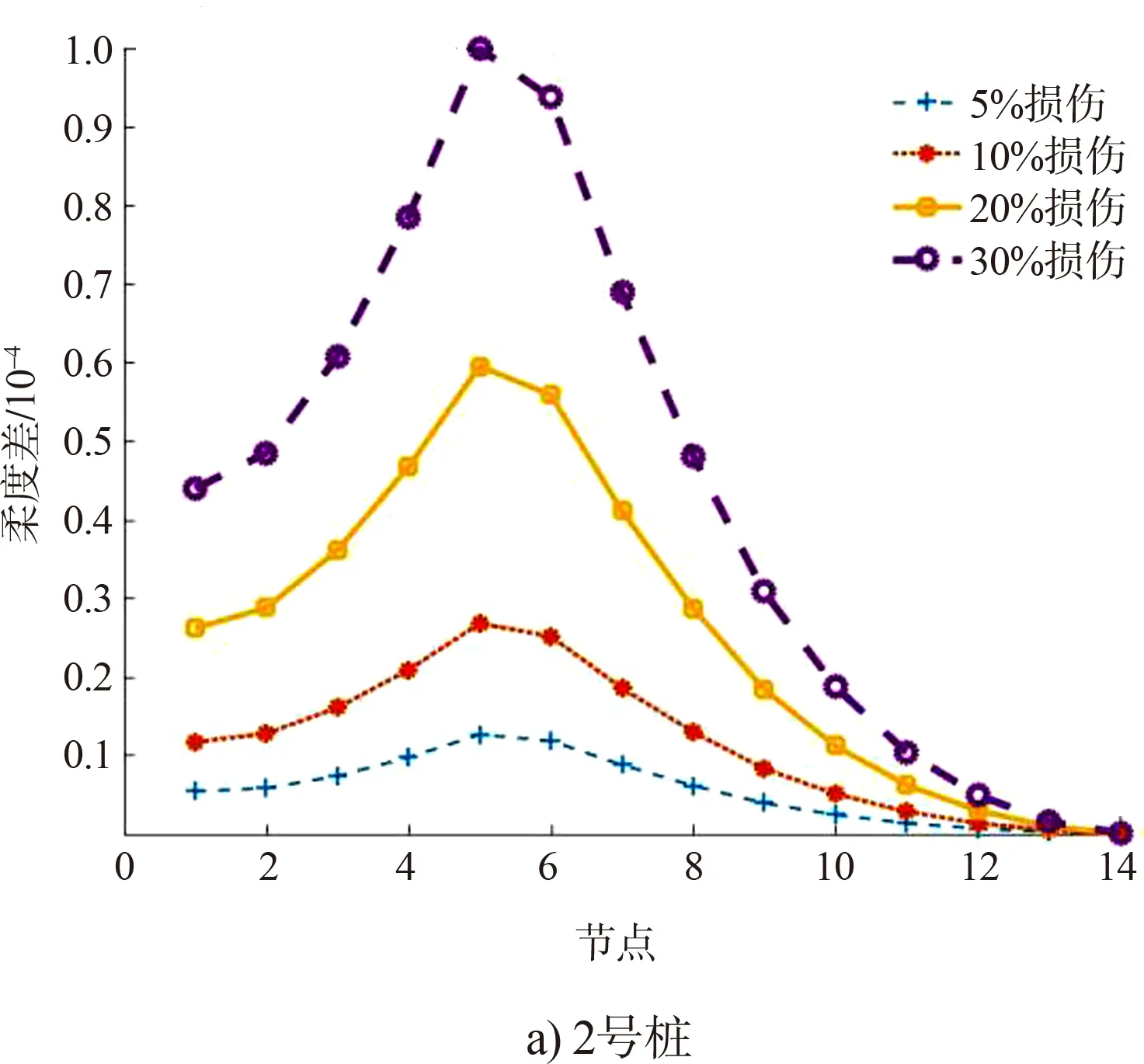

图4 有限元各工况模态柔度变化量
3 基于动力试验的模态柔度损伤识别
3.1 动力测试试验
高桩码头物理模型几何尺寸、桩身分段及节点编号与有限元模型相同。结构分段上部横梁、纵梁、面板采用C60混凝土浇筑,桩身采用Q235钢管桩,钢管桩底部用10 cm混凝土固定,底部混凝土固结在地面上。试验模型见图5,桩身损伤通过减小桩身截面尺寸实现。动力测试采集设备采用DH5920动态信号采集分析系统,单通道采样频率1 kHz;拾振器采用YD-186型压电式加速度传感器,传感器频响范围0.2~6.0 kHz,灵敏度(100.03)mVms2。在1~28号节点上布置26个传感器(桩身最下面节点14号节点和28节点未布置加速度传感器),桩身传感器布置见图6。模态测试通过用橡皮锤随机敲击码头不同位置来采集桩身加速度时程响应。

图5 码头试验模型

图6 2号桩身加速度传感器布置
3.2 动力测试试验与有限元计算的相似性验证
根据锤击下的加速度时程响应,采用随机子空间方法进行模态分析得到码头模型的固有频率和振型,码头模型试验测试频率与数值模拟对比见表1。从表1可以看出,码头模型实测频率与有限元计算频率非常接近,最大误差不超过4%。试验振型与有限元计算振型相似性验证见图7(本文仅列出了2号桩完好工况和10%损伤的振型对比)。从试验振型与有限元计算振型对比可以看出,试验分振型与有限元计算结果非常贴近,物理模型与有限元模型动力特性相一致。

表1 试验测试频率与数值模拟对比
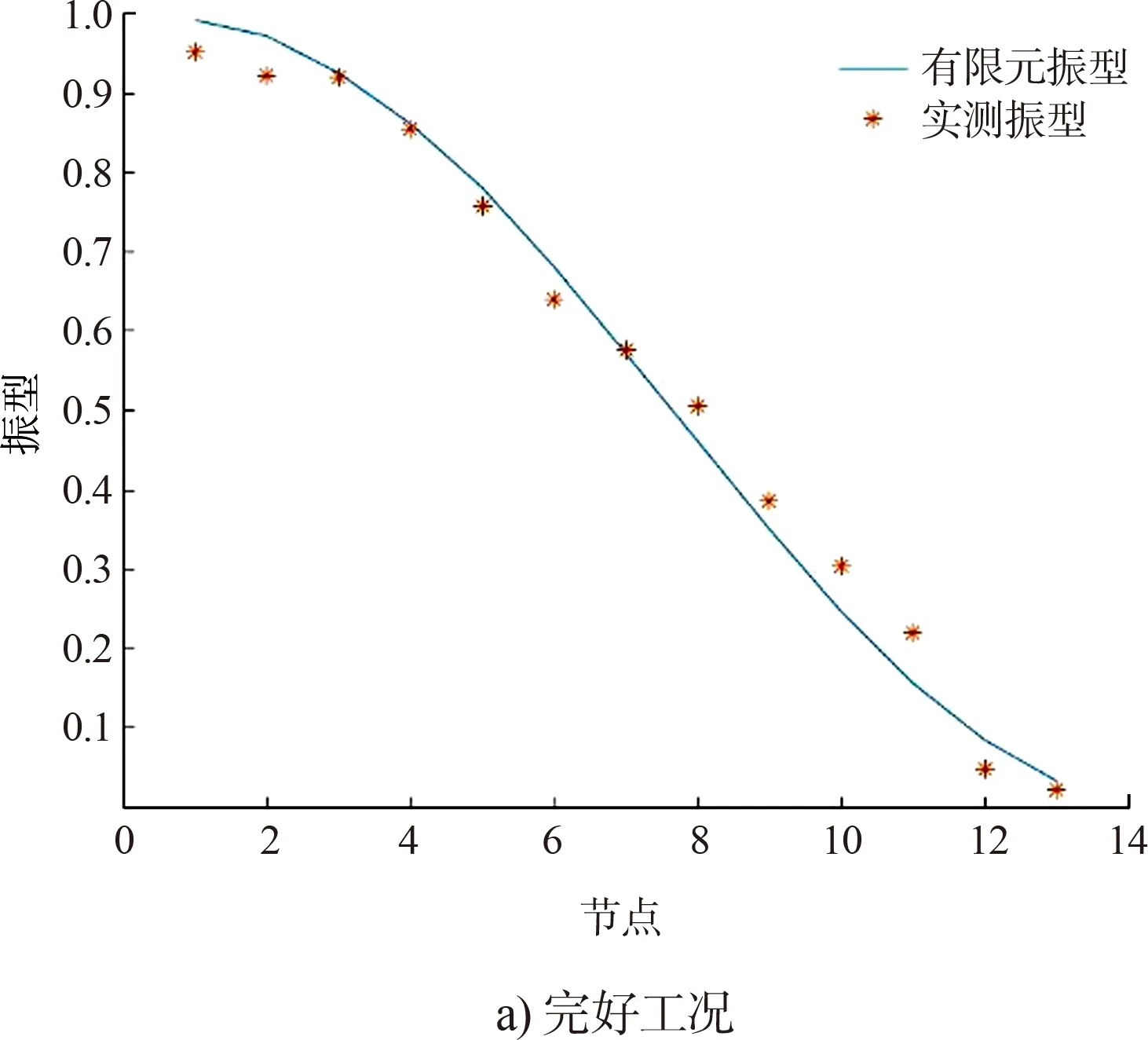

图7 2号桩试验振型及与有限元振型对比
3.3 动力试验损伤识别结果
基于试验模态计算各工况模态柔度,进行码头桩基损伤识别,图8列出了各工况下的模态柔度变化曲线。从图8可以看出,基于试验测试的模态柔度可以识别结构损伤位置,变化量在损伤位置均有“尖峰”出现,同时可以看出,试验桩基模态柔度损伤识别存在以下缺陷:
1)模态柔度变化量曲线出现扰动。由于试验振型测量存在随机误差,基于实测振型计算模态柔度时误差会放大。振型的测量精度低是现阶段普遍存在的问题,文献[9]指出“由于振型在实际测量中精度低,受环境噪声干扰大。对于复杂的结构,其低阶的振型也很难准确测量。振型在动力测试中的困难大大限制了它在实际工程中的应用”。
2)边界数据规律性差。模态柔度边界特别是底部和有限元计算规律差别较大,这是由于模型试验中边界条件不能实现有限元中的完全固结所导致的。
3)不同程度不能准确体现。如图8b)中3号桩模态柔度变化量5%损伤工况“尖峰”比10%损伤和20%损伤大,10%损伤和20%损伤接近,其原因是由于试验测试误差和模态识别误差共同叠加所致,特别是大型工程结构模态识别通常采用的随机子空间法会存在一定误差[10]。
综上所述,由于振动试验的模态柔度可以进行桩身损伤识别,但其精度受当前动力测试分析技术的限制,模态柔度的广泛工程应用还需要振动测试分析技术的进一步发展。

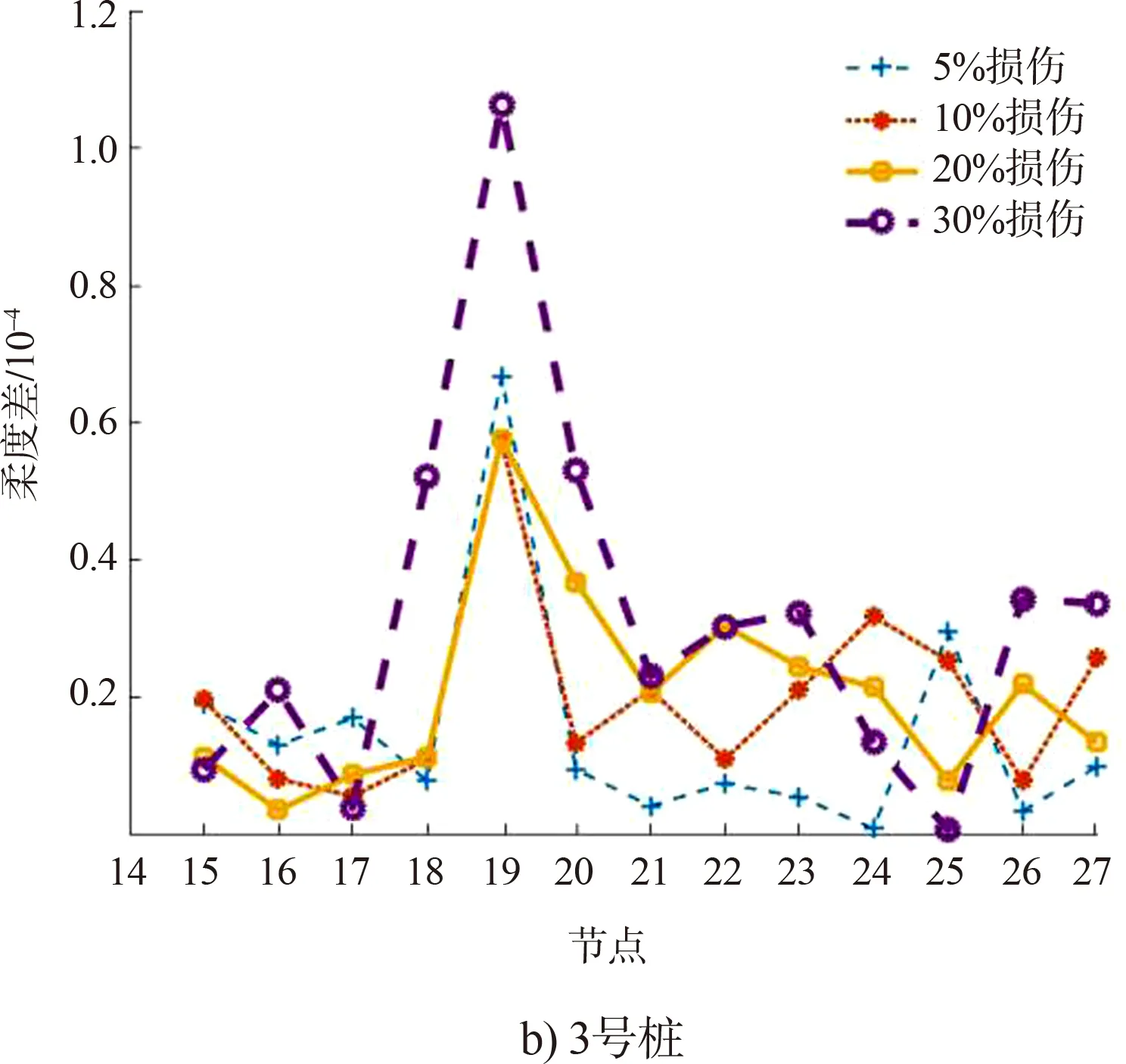
图8 实测桩各工况模态柔度变化量
4 结语
1)基于有限元模拟计算振型研究了模态柔度对高桩码头桩基损伤的识别效果,结果表明在有限元模拟中模态柔度可准确识别损伤所处位置,并且损伤程度越大模态柔度变化量越大,模态柔度可定性反映结构损伤程度,为高桩码头桩基损伤识别应用提供理论基础。
2)通过高桩码头动力试验测试振型研究了模态柔度对高桩码头桩基损伤的识别效果,结果表明基于试验振型得到的模态柔度可反映损伤位置,但由于测试噪声和试验误差的存在,损伤识别效果没有基于有限元计算振型理想。
3)动力损伤识别理论目前已基本成熟,其在大型工程中的广泛应用还需要动力测试技术、模态分析技术的进一步发展。

