海堤越浪量的物理模型试验及人工智能算法模型预测*

倪 琦，范红霞，刘 涛，倪兴也

(1.中国人民解放军91053部队，北京100070；2.南京水利科学研究院，江苏 南京210029；3.河海大学 港口海岸与近海工程学院，江苏 南京 210098)

海堤作为一种常见的水工建筑物，主要用来保护沿海地区免遭波浪、潮流等自然灾害的侵袭和破坏。理论上，海堤设计高程超过波浪爬高，堤后就没有越浪产生，对于堤后建筑物的保护最为有效。考虑到实际工程设计的经济适用性，《港口与航道水文规范》[1]规定在一定范围内允许部分越浪产生。对于越浪量有较高要求的渔港、煤气码头等重点设施需要严格控制越浪量。因此明确影响越浪产生的因素和准确预测越浪量的大小对于防护海岸及海洋工程是十分关键的。

海洋中的波浪多为不规则波，不规则波的随机性导致不同波列产生的越浪量差别较大，所以一般用单位时间单位宽度的平均越浪量来衡量越浪量的大小。从20世纪50年代开始，越浪量的相关研究就成为国内外学者关注的焦点问题。Saville[2]进行了规则波在斜坡堤上的越浪量试验研究。后来Yuichi等[3]在Saville的研究基础上，总结了波高和水深对越浪量的影响。Owen[4]通过物理模型试验对海堤越浪量进行了系统研究，指出越浪量主要受波浪爬高、波浪破碎以及风的影响，并提出了光滑不透水板铺设的斜坡堤越浪量计算公式。欧洲国家普遍采用Meer等[5]提出的越浪量计算公式，他的公式主要考虑了前坡坡度、堤前地形、平台宽度及高度、波浪入射角度以及前坡糙率的影响。我国对海堤越浪量的研究始于章家昌等[6]和王红等[7]，其相应的研究成果被写入《港口与航道水文规范》，后来国内的学者在此基础上开展了各种研究。范红霞[8]、陈国平等[9]、周雅等[10]、孙大鹏等[11]均根据自己的研究结果提出了海堤越浪量计算公式。

综上所述，越浪量的影响因素众多，且越浪量与各个影响因素之间存在复杂的非线性关系，难以使用传统的公式拟合方法准确得到，致使前人提出的计算公式具有较大的差异性。近年来，人工智能算法的发展为复杂的海洋问题带来了新的解决方法，BP(back propagation，反向传播)神经网络的自组织、自适应和自学习等运行机制可以很好地适用于越浪量的预测计算。本文主要分为两部分：1)通过物理模型试验来探究不同影响因子对海堤越浪量的影响；2)根据物模试验结果，基于人工智能算法构建越浪量的预测模型。

1 试验概况

试验在南京水利科学研究院河港研究所波浪水槽中进行，试验布置如图1所示。水槽长62 m、宽1.8 m、深1.8 m，水槽沿宽度方向分成0.6和1.2 m两部分，试验段设在0.6 m宽部分，另一部分用于消除波浪二次反射的影响。水槽两端均设置消浪缓坡，以减少波浪反射。波浪水槽一端配有丹麦水工研究所生产的推板式造波机，用以产生所需波要素。接水箱置于试验断面后方，越过的波浪由0.2 m宽的接水板引流到接水箱上，通过底部放置的压力传感器进行采集，采样时间间隔为0.1 s。

图1 试验布置(单位：m)

物模试验采用重力相似准则，模型比尺1:20。本次试验采用不规则波，波谱为JONSWAP谱，谱峰升高因子γ=3.3。试验波要素组合为：有效波高Hs为0.15、0.20 m，平均周期Tm为1.3、1.5、2.0、3.0 s。水深d保持恒定为0.4 m。试验断面如图2所示，护面采用光滑不透水混凝土板，前坡坡度为1:2，后坡为1:1.5。防浪墙采用直立式，高度P取0、0.05、0.10、0.15 m。墙顶超高Hc分别为0.20、0.25、0.30、0.35 m。堤顶肩宽b为0、0.05、0.10、0.15、0.20、0.30 m。

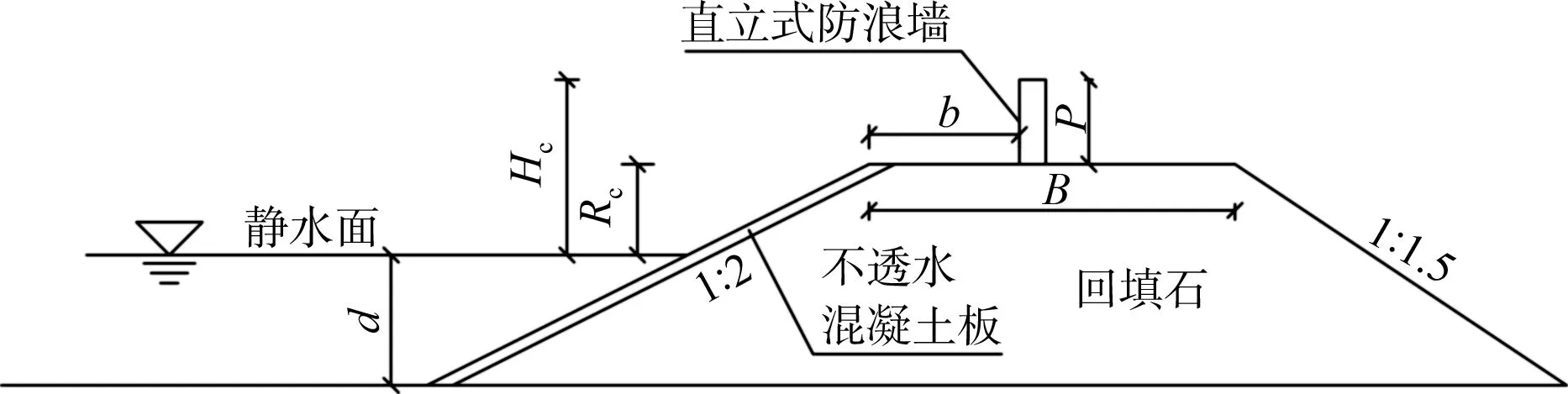
图2 试验断面

2 试验结果与分析

影响海堤越浪量因素众多，如设计水位、设计波要素、海堤结构形式、海堤堤身尺寸、堤前海底地形以及风况等。若要对各个影响因素进行系统分析，工作量巨大且繁琐，较难在一个试验中实现。因此本次试验主要探究波浪要素(有效波高Hs、平均周期Tm)、防波堤外形(防浪墙高度P、堤顶超高Hc)和防浪墙摆放位置(堤顶肩宽b)对海堤越浪量的影响。

爬高至平台的水体遇到防浪墙的阻挡，改变了水体的运动状况，一部分水体被挡于墙前，另一部分水体越过防浪墙进入堤后，防浪墙高度直接影响越浪量的大小。不同周期下相对防浪墙高度PHc对相对越浪量的影响见图3c)。可以看出，总体上随着PHc的增大而减小，但在不同周期下，随PHc的减小趋势略有不同。主要体现为周期较小时，减小的趋势更为平缓，与PHc呈指数分布。

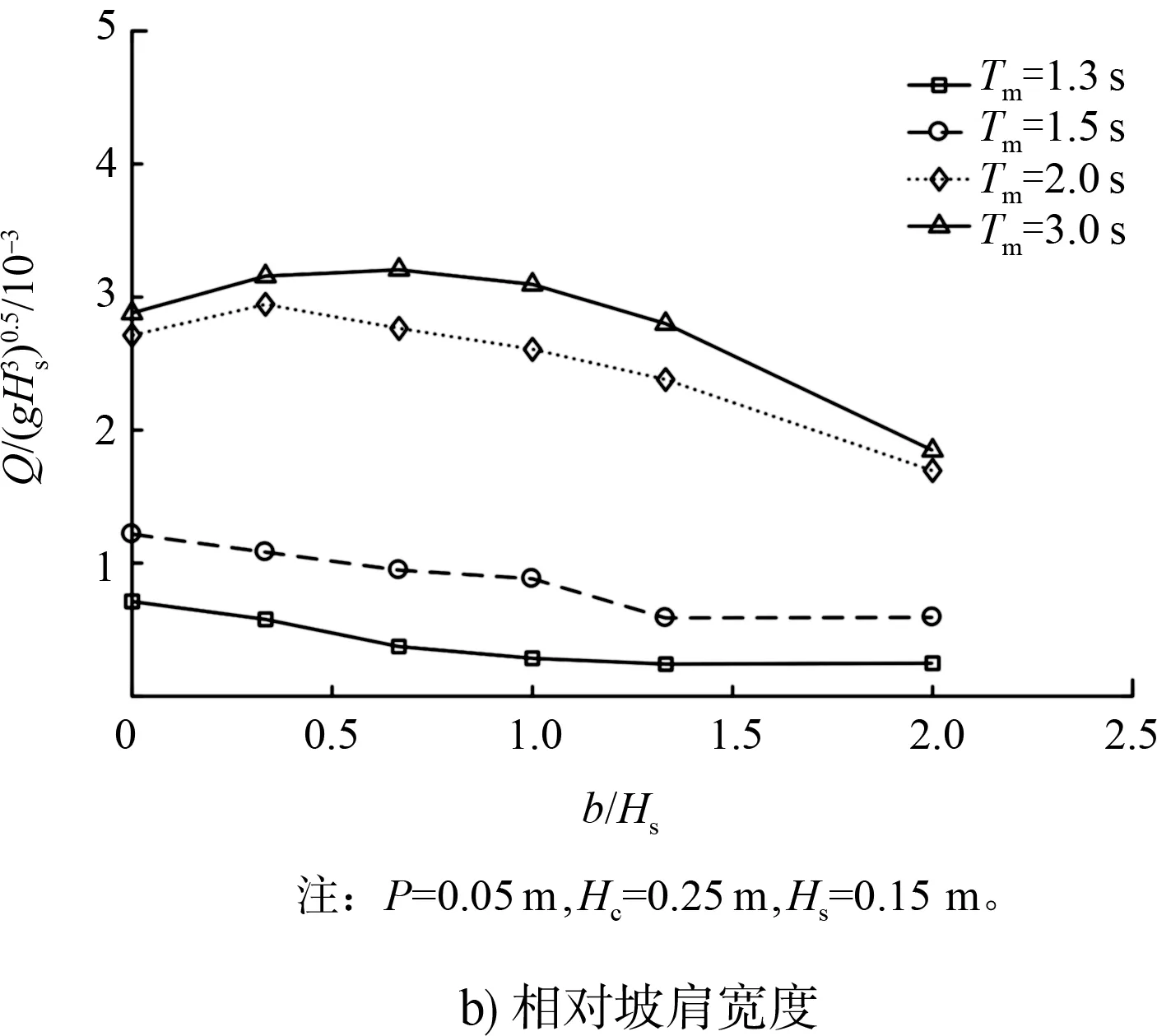
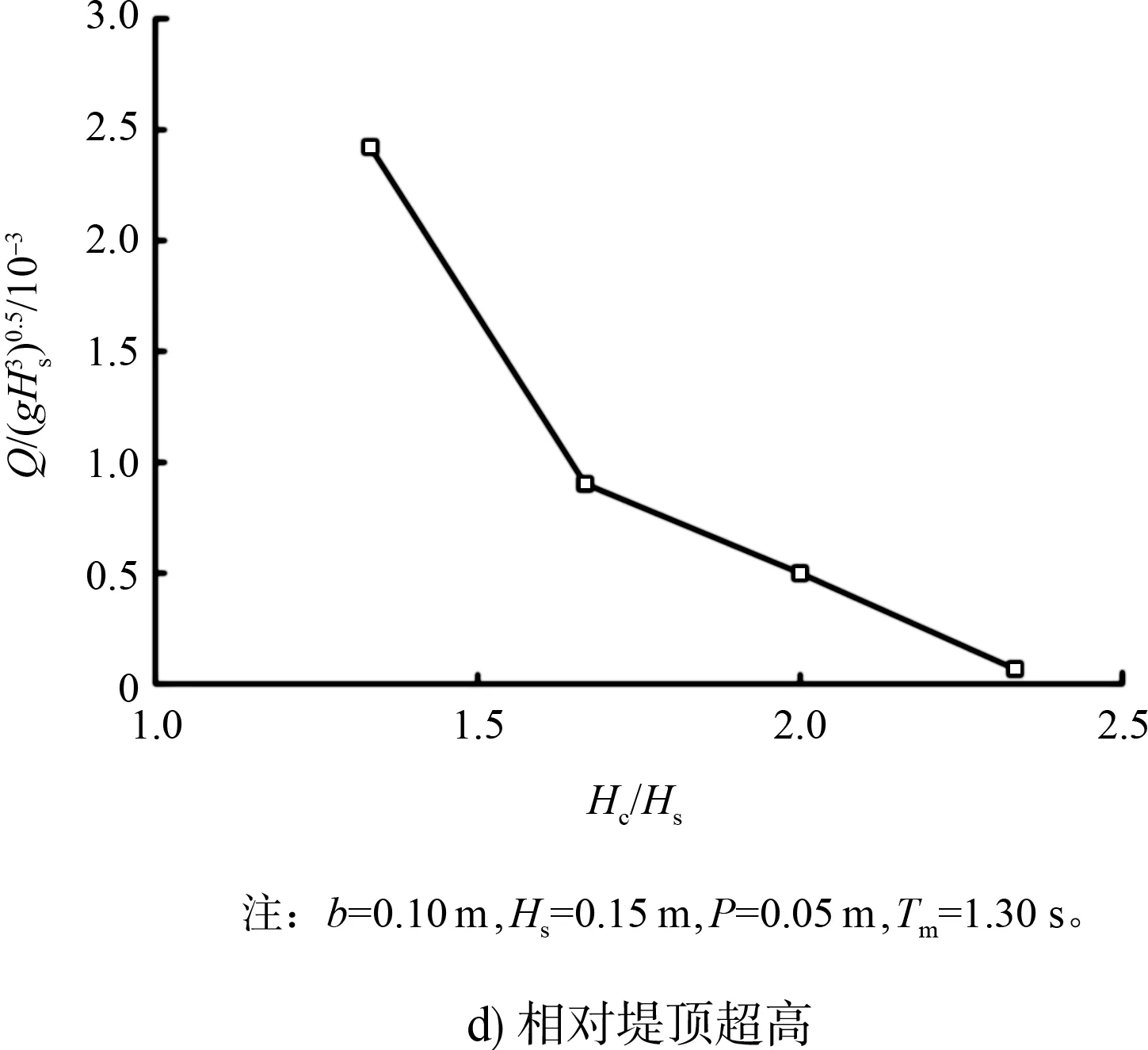
图3 相对越浪量随各影响因素变化曲线

3 人工智能算法构建预测模型

3.1 人工智能算法

本文采用BP神经网络预测越浪量。BP神经网络的学习过程采用误差反向传播、信号正向传播，不断调整网络的阈值和权值，使误差最小化，是运用最广泛的一种神经网络[12]。输入层、隐含层和输出层是BP神经网络的3层网络结构，如图4所示。输入层的因子输入和隐含层节点数量对于模型的性能有着重要影响。

图4 BP神经网络结构

3.2 预测模型构建

3.2.1数据选择及归一化处理

考虑到不规则波的随机性以及试验过程中不可避免存在操作或系统误差，本文先对试验数据进行了校核选择，剔除明显错误的和重复的数据，最后确定了120组有效试验数据。

因为试验数据的各项处于不同数量级，直接运用会出现“大数吃小数”的现象，降低了部分数据的重要性，不利于模型的构建。为了避免上述情况发生，同时加快模型的收敛速度，需要对数据进行归一化处理，使得数据映射到(0，1)之间，归一化公式如下：

(1)

式中：Y为数据归一化后值；x为数据归一化前值；xmax、xmin分别为数据归一化前的最大值、最小值。

本次论文中数据的归一化采用Matlab软件中的函数mapminmax(x，0，1)。

3.2.2输入、输出因子

3.2.3BP神经网络模型参数设置

随机选择90组数据用于模型训练，18组数据用来模型验证，剩余的12组数据用来测试模型的泛化性能。

1)隐含层节点。根据文献[13]的研究，隐含层节点数J=(m+n)0.5+a，其中m为输入层节点数，n为输出层节点数，a为1～10的常数，所以J∈[3，13]。隐含层节点数与训练误差如图5所示。可以看出，当节点数为10，模型的均方差最小，所以本次模型的隐含层节点数设置为10。

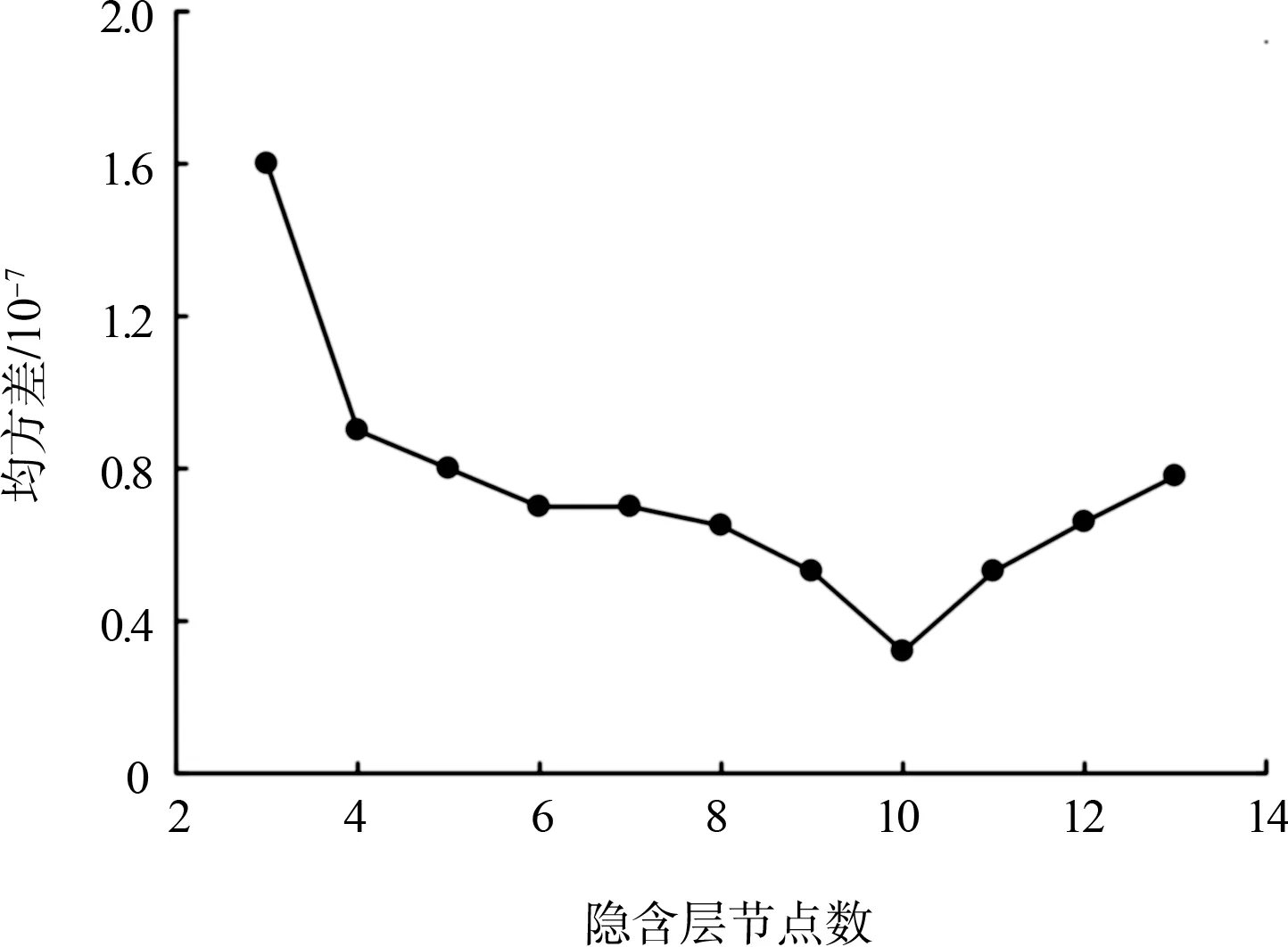
图5 隐含层节点对训练集性能影响

2)基本参数设置。考虑到L-M(Levenberg-Marquardt)算法收敛速度快，预测精度高，是中型算法里的首选算法，本文选择L-M算法训练模型。隐含层传递函数选择tansig函数，输出层传递函数选择pureline函数，进化代数选择1 000代，学习效率设为0.01，目标精度设为1×10-7，动量因子选择0.9。

4 人工智能算法预测模型结果分析

4.1 模型训练

将90组数据利用BP神经网络模型进行训练，训练值与模型输出值的线性回归分析结果如图6a)所示，同时引入了基于遗传算法优化的基因表达式编程(GEP)算法[14]用于对比分析，结果如图6b)所示。两图中实线均为45°理想线，数据点越接近实线说明预测效果越好。对比图6a)、6b)可以看出，BP神经网络的预测值更为理想，数据点基本落入45°理想线附近，GEP算法的预测值偏差较大，结果较为发散。BP神经网络模型的预测值和试验值相关系数R达到0.99，均方差MSE为8.2×10-8，相比之下，采用GEP算法训练的结果R为0.86，MSE为7.1×10-7，误差超过一个量级。

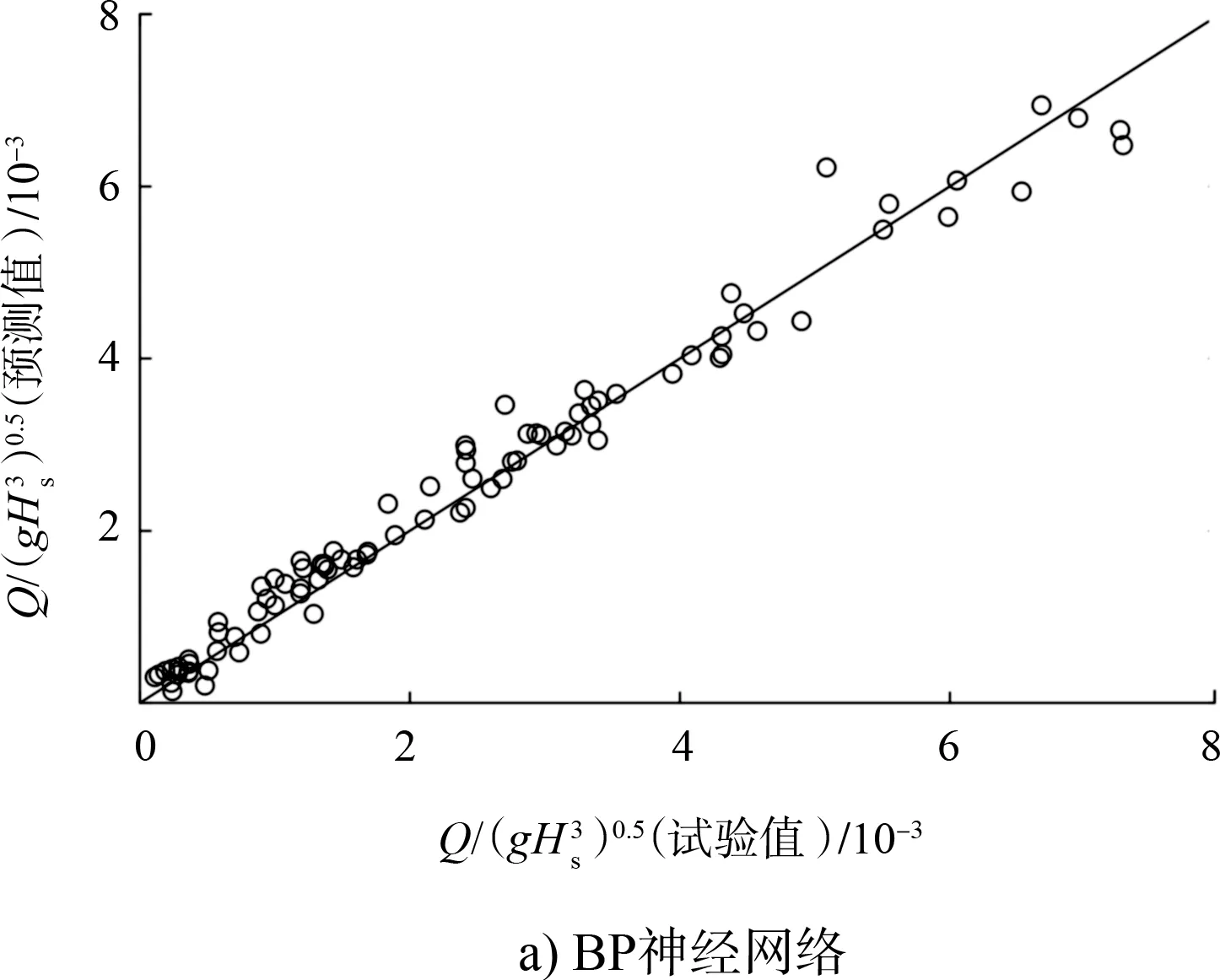
图6 BP神经网络模型和GEP算法训练集输出回归分析

4.2 泛化性能

为了验证模型的泛化性能，将已建立的模型测试从未参与训练的12组数据，结果如图7所示。可以看出，GEP算法的预测结果不太理想，整体上数据的趋势走向与试验值是一致的，但是部分数据点的误差较大，可信度不高。采用BP神经网络模型预测结果与试验值非常吻合，数据的波动趋于一致，部分数据点存在一定重合，模型的预测值与试验值更加接近，精度更高，说明采用BP神经网络模型用来预测越浪量具有较高的可靠性。

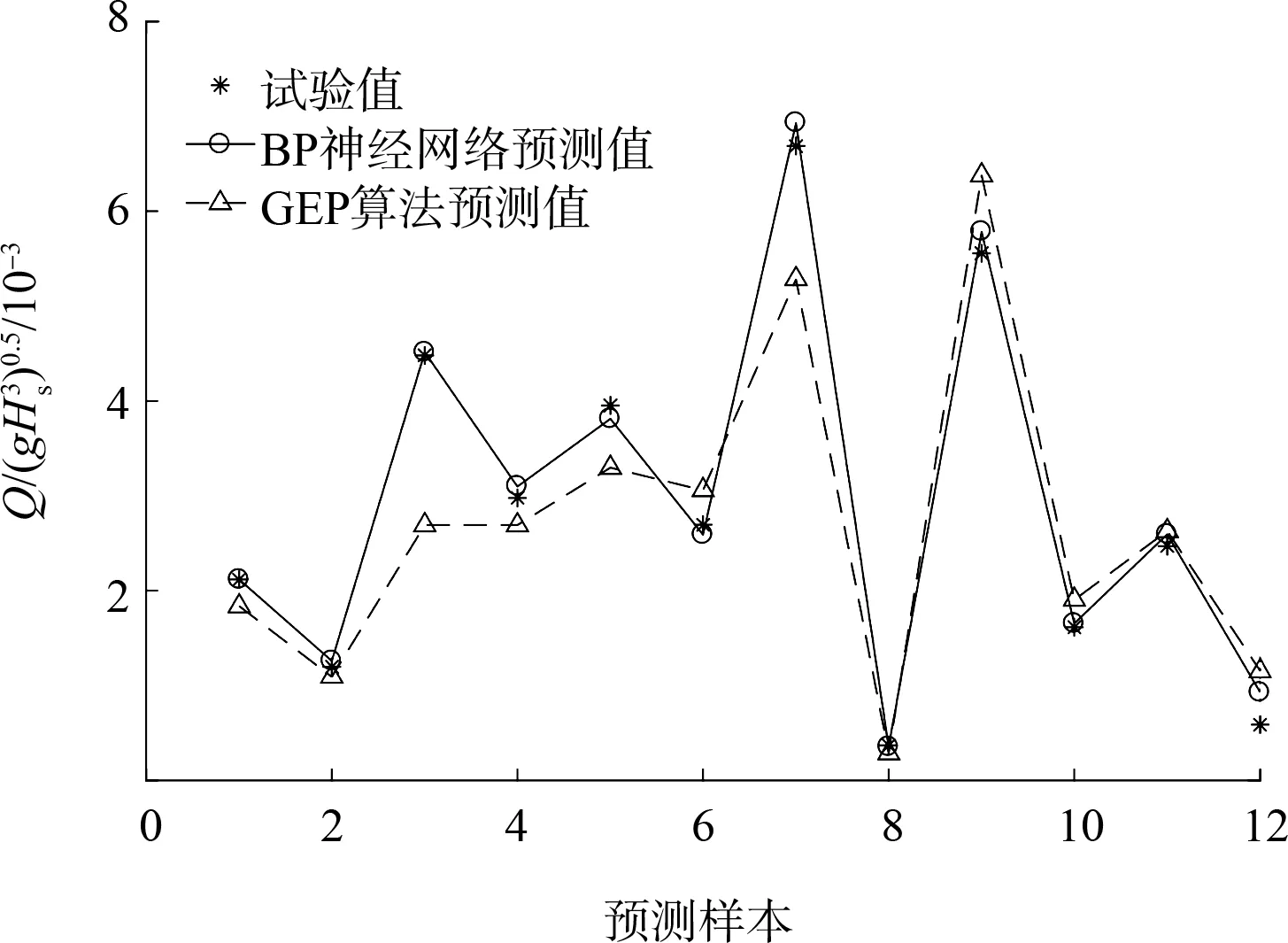
图7 BP神经网络模型与GEP算法的预测结果比较

为了定量展现模型的预测精度，将BP神经网络模型和GEP算法的预测误差绘制成直方图，如图8所示。可以看出，采用BP神经网络模型预测，落入±5%误差的样本点占比达到83%，超过90%的样本数据误差在±10%以内，预测结果较为满意。而GEP算法的预测误差主要集中在-40%～18%，远高于BP神经网络模型。值得注意的是，两个模型对第12号样本点的预测误差明显超过正常范围，这可能是试验数据本身存在的系统误差，不足以说明模型的好坏。

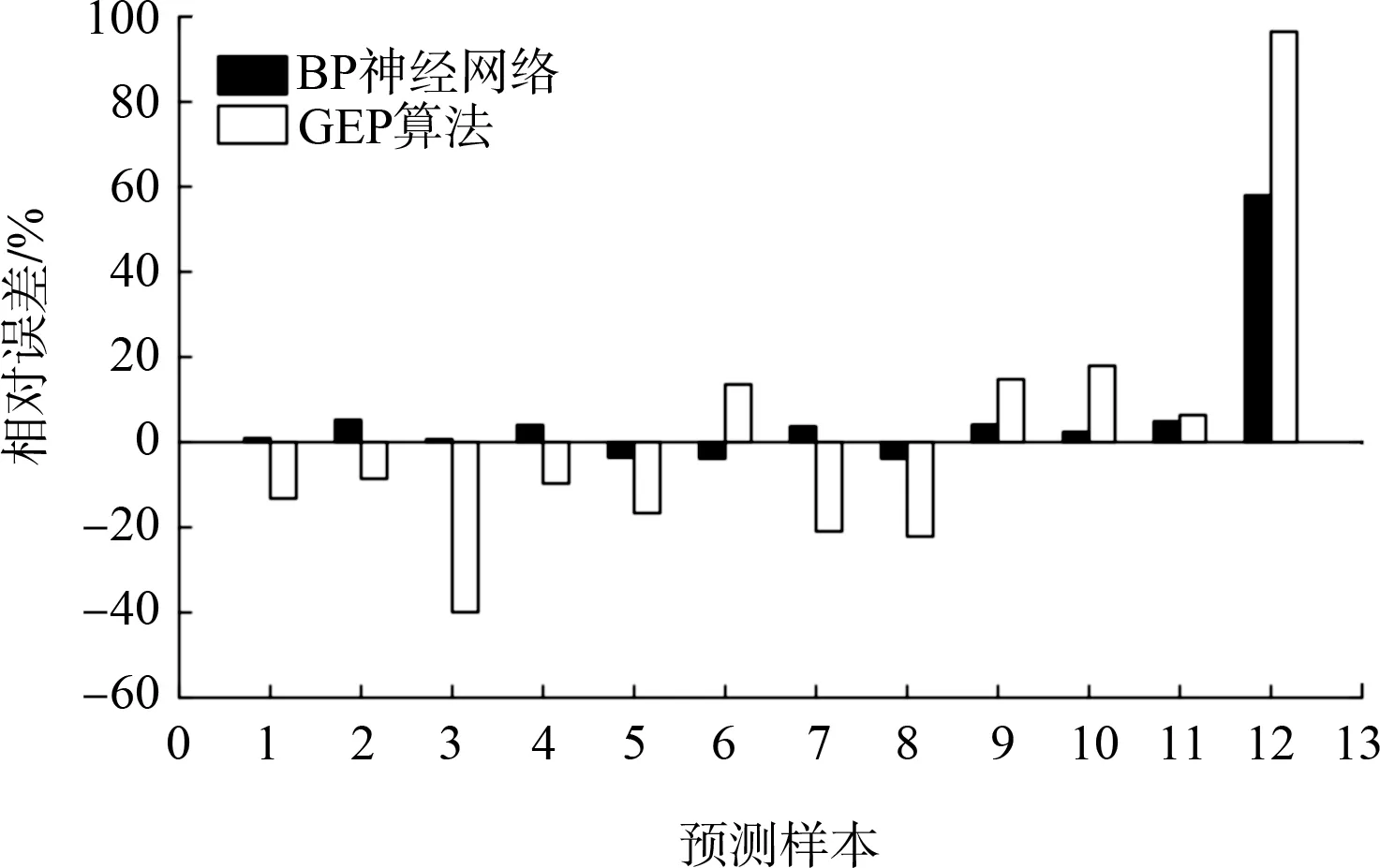
图8 BP神经网络模型与GEP算法的预测误差

4.3 实际工程验证

影响越浪量的因素众多，精准预测越浪量是十分困难的，因此国内外公式一般控制在10倍误差范围内，即一个量级以内[15]。本文除了对已有的试验数据进行测试外，还采用实际工程项目试验数据测试模型的适用性，数据来源于广东省水利水电科学研究院和河海大学海岸及海洋工程研究所的研究报告[16-17]，验证结果如图9所示，虚线之间的部分为5倍误差区间带。可以看出，BP神经网络模型对实际工程项目越浪量的预测值与试验值较为吻合，数据全部落入误差区间带内，进一步表明该模型具有良好的泛化能力和应用前景。

图9 实际工程项目中试验值与BP神经网络模型预测值比较

5 结论

1)当肩宽较小时，相对越浪量随着平均破波参数的增大而迅速增大，ξ=2.5时达到最大，且相对越浪量随着平均破波参数的继续增加而略有减小。当肩宽较大时，相对越浪量随平均破波参数的增大而增大，在ξ=2.5附近出现分界，相对越浪量的增大趋势逐渐放缓。

2)相对越浪量随相对坡肩宽度和相对防浪墙高度的增大而减小，坡肩越宽、防浪墙高度越高，消浪效果越显著，且越浪大小受波浪周期影响。

3)海堤肩宽、防浪墙高度、入射波高和波周期保持恒定，相对堤顶超高较小时，相对越浪量随着堤顶超高的增大而迅速减小，随着堤顶超高的继续增大越浪量逐渐呈线性减小。

4)基于人工智能算法建立的模型可以较好地预测海堤越浪量大小。训练组中模型的预测值和试验值相关系数达到0.99，均方差为8.2×10-8，测试组中超过90%的数据预测误差控制在±10%范围内，且模型在实际工程项目中验证表现良好。建立的模型具有良好的预测精度和泛化性能，可为未来的工程设计及后续的越浪研究提供参考。