基于MSRCR 的水下图像增强算法研究

王浩然， 余 粟， 燕雨薇

（1 上海工程技术大学 电子电气工程学院， 上海201620； 2 上海工程技术大学 第二图文信息中心， 上海201620）

0 引 言

中国海域辽阔，拥有约300 万平方公里的海洋国土面积。 近年来深海信息技术迅猛发展，海洋资源的勘探和利用对我国的国民经济和国防安全愈发重要。但是恶劣的水下光学成像环境导致获取到的水下图像广泛存在对比度低、模糊、偏色等问题，严重阻碍了水下活动的正常进行［1］。 目前Retinex 算法及其衍生的单尺度、多尺度Retinex 算法和MSRCR 算法广泛用于图像增强，但是处理后的水下图像仍存在一定失真。 文献［2］先通过大气光暗原色先验去雾算法提高水下图像清晰度，再通过透射率自适应调节提高图像清晰度，但是处理后的图像整体偏暗。 文献［3］提出了基于模糊形态和四元数的水下彩色图像增强方法，但是处理后的图像对比度不高。 文献［4］提出了基于多尺度Retinex 的非下采样Contourlet 域图像增强方法，但是处理后的图像色彩失真。

针对上述问题提出了一种基于MSRCR 的水下图像增强算法。 首先经MSRCR 算法对水下图像进行预处理，改善水下图像偏蓝绿色彩失真状况；然后经直方图拉伸拓展预处理后图像的灰度分布，提高对比度；再对图像进行伽马变换突显细节；最后采用引导滤波对图像平滑去噪。

1 Retinex 理论及MSRCR 算法

Retinex 是视网膜（retina）和皮层（cortex）两个单词的合成，所以Retinex 理论也被称为视网膜皮层理论。 该理论的基本思想是光照强度决定原始图像像素动态范围，而原始图像的固有属性则由物体自身的反射系数决定，即原始图像为反射图像和光照图像乘积。 因此Retinex 理论本质就是去除光照影响，保留住物体的固有属性。 假设观察者观察的图像为I（x，y），则表达式为：

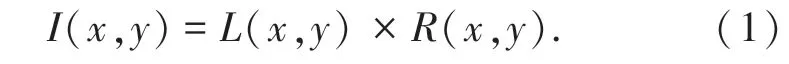
式中：L（x，y） 表示光照分量，R（x，y） 表示物体本身固有性质的反射分量。 对公式（1）两边做对数处理：

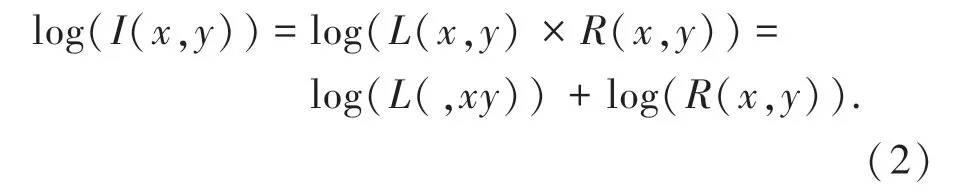
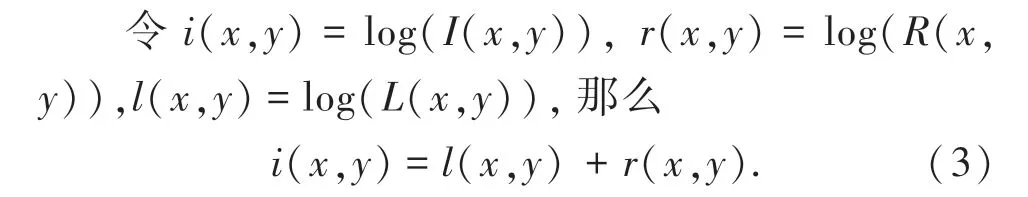
上面作对数处理的两大好处是：（1）人眼对亮度的感知能力近似于对数曲线不是线性的；（2）复杂的乘除在对数域中是简单的加减法，可以大幅度降低算法的复杂度。 MSRCR 算法是Retinex 的一种，因为SSR［5］和MSR［6］算法易产生色差，所以研究者们又提出了新的算法，即带颜色恢复的多尺度Retinex（MSRCR）算法。 MSRCR 的数学表达式为：

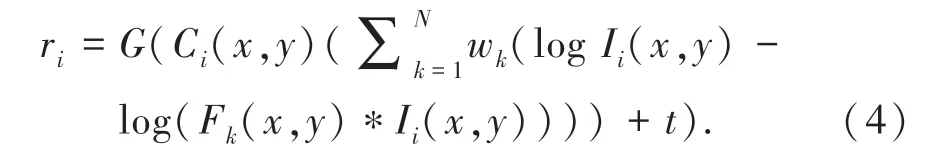
其中，G 和t 分别是增益和偏移量系数，作用是较好地将图像显示在屏幕中；Ci（x，y） 是i（i ∈｛r，g，b｝） 颜色通道的恢复因子；wk是第k 个尺度加权权重系数，它需要满足＝1； Fk（x，y） 是在第k 个尺度上的高斯滤波函数。

2 水下图像增强方法

就水下图像易出现的色彩失真、对比度不高问题，提出基于MSRCR 的水下图像增强方法。 经本算法处理后的水下图像对比度、清晰度都得到大幅提高、图像层次分明以及处理后的图像色彩恢复效果也更好。 本文算法流程如图1 示。

图1 算法流程图Fig. 1 Algorithm flow chart

具体步骤为：（1）输入水下彩色图像A 先经过MSRCR 算法预处理，得到图像B；（2）对图像B 进行直方图拉伸处理即拓宽图B 的灰度级分布范围，使图像层次分明从而得到图像C；（3）对图像C 进行伽马变换得到图像D，进一步提高图像对比度和整体亮度；（4）对图像D 进行滤波去噪得到最终图像E，去噪后图像更加清晰；（5）最后，用4 种指标对图像B 和图像E 进行比较，得出结论。

2.1 直方图拉伸

直方图拉伸的作用是扩展图像灰度分布，提高图像对比度。 图2 为实验图水下人与铜像经拉伸前后直方图对比。 由图可知，直方图拉伸可以使得图像灰度级分布更加均匀，把原本密集的灰度级分布展开。

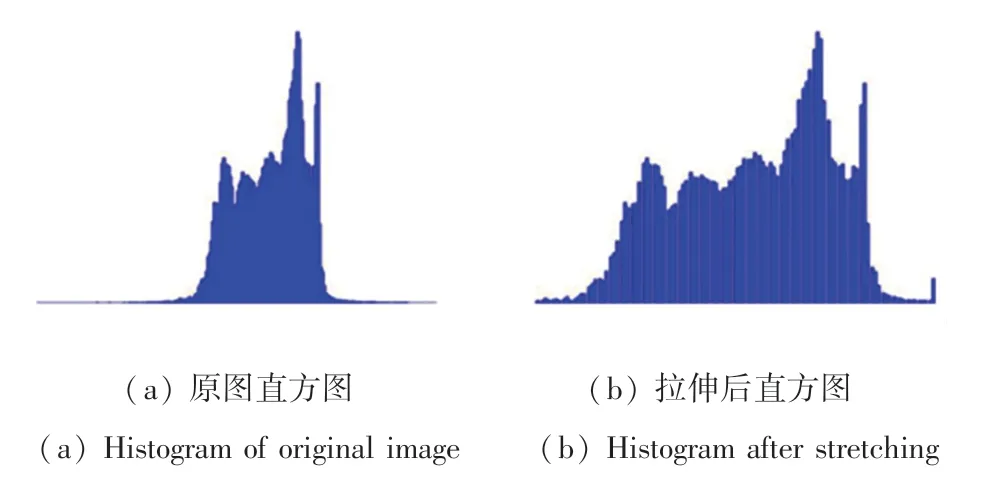
图2 水下人与铜像直方图Fig. 2 Comparison of underwater man and copper image histogram

图3 为水下人与铜像灰度图，从图3 可以看到，拉伸后的灰度图像b 比拉伸前原图灰度图更清晰同时亮度也得到一定提高。

图3 水下人与铜像灰度图Fig. 3 Underwater man and grayscale of bronze image

2.2 伽马变换

虽然拉伸后图像灰度图比原来图像灰度图更清晰，因为从图2 可以看到，经拉伸后图像直方图分布范围更广，灰度值更加均匀，但是从图3（b）可以看出，经拉伸后的图像灰度图层次不显著，对比度仍有较大提高空间。 因此，在直方图拉伸后，使用伽马变换来进一步提升图像对比度，使得图像更有层次感。图像伽马变换的基本形式为：

在此假定c ＝1，得到不同γ 值的伽马曲线，如图4 所示。

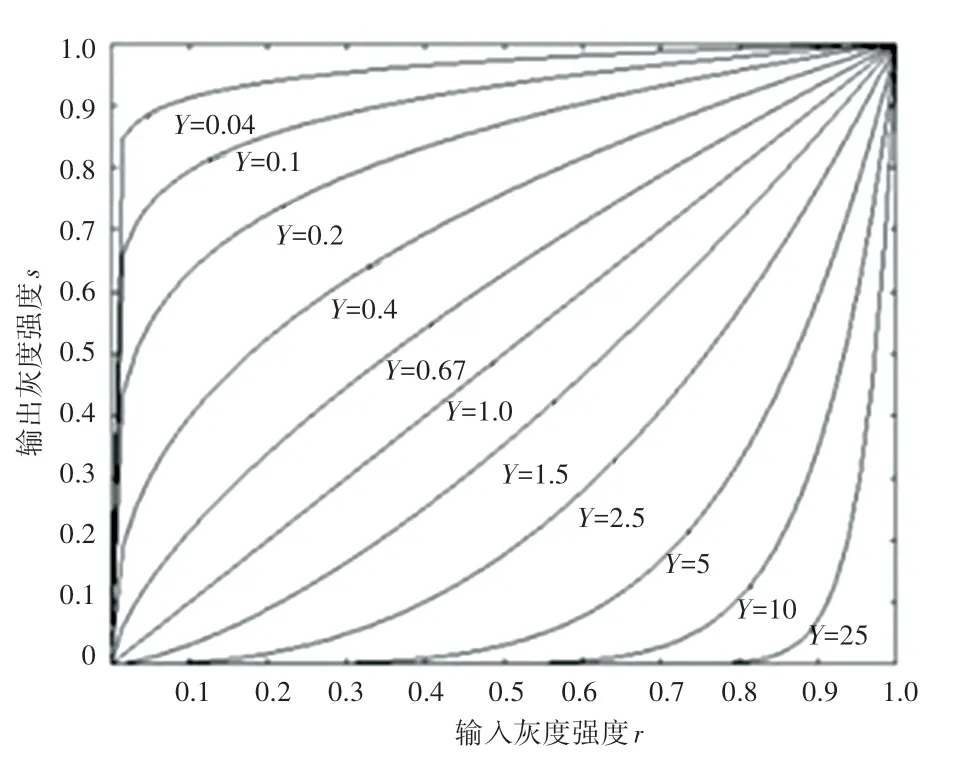
图4 伽马曲线Fig. 4 Gamma curve

伽马变换的作用是增强图像灰度值，增加图像对比度。 由图可知，如果图像整体偏暗，就选择γ ＜1，可以增强图像亮度；反之，如果图像整体灰度偏亮时，则选择γ ＞1，可以使图像变暗、突显图像细节以及提高图像对比度。 在本研究中为了得到最优的伽马变换结果，经反复测试最终选取伽马值为2。图5 为经过伽马变换后的图像。

图5 伽马变换后的图像Fig. 5 Image after gamma transform

与图3（b）相比，经伽马变换后的图像局部亮度和对比度都有所提高。 但图5 还有一些噪声信号，使得图像看起来模糊。 故本文引入滤波方法来去噪。

2.3 滤波处理

引导滤波器（guided image filter）［7］和双边滤波器（bilateral filter）［8］在滤波过程中都能够有效保留图像中边缘信息，所以又称为保边滤波器（edge preserving filter）。 鉴于引导滤波在写出时间复杂度与窗口大小无关算法方面比双边滤波更有优势以及引导滤波使用大窗口处理图片时，效率更高，故本文选用引导滤波对伽马变换后的图像进行去噪。

假设p 为输入图像，q 为输出图像，I 为引导图，q与I 在以像素k 为中心的窗口中具有局部线性关系：

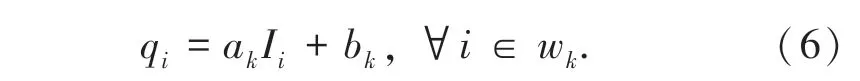
其中，q 是输出像素值，I 是输入像素值，i 和k 是像素索引，a 和b 是当窗口中心位于k 时此线性函数的系数。 这个模型保证了只有在I 存在边缘的情况下，q 才会存在边缘。 这是因为：∇q ＝a∇I。 q 即p去除噪声或者纹理之后的图像：

为确定以上公式中的线性系数，并使得q 与p的差别最小，转化为最优化问题：

其中，p 是待滤波图像，ε 是对过大a 值进行惩罚的正则系数。 通过最小二乘法，我们可以得到：

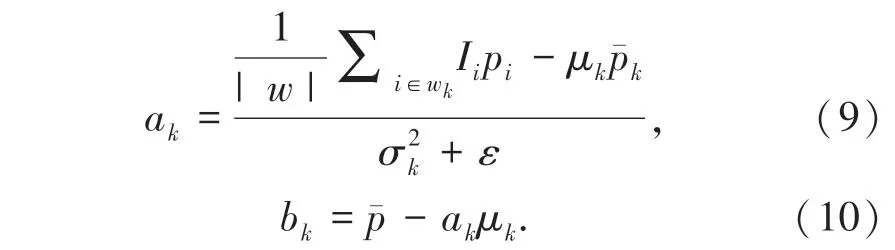
其中，μk是引导图I 在窗口wk中的平均值，是引导图I 在窗口wk中的方差，｜w ｜是窗口wk中像素总数量，p是待滤波图像p 在窗口wk中的均值。

最后输出图像数学表达式为：

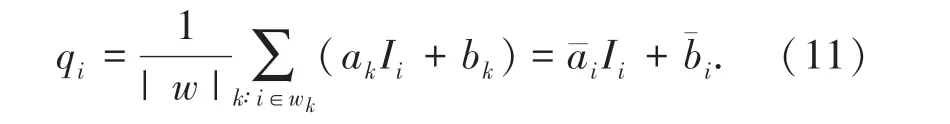
其中，wk是所有包含像素i 的窗口，k 是其中心位置。 引导滤波结果如图6 所示。 与图5 相比，经滤波处理后的图像更加平滑，整体亮度也更高，对比度进一步提高，这就是所提算法的最终处理结果。

图6 引导滤波处理后图像Fig. 6 Image after guided filtering

3 实验与分析

为了验证本文算法的有效性，从百度水下图像库中选取多幅不同场景的水下图像进行增强处理，选取3 组不同光衰减性、后向散射性和不同浑浊程度的水下彩色图像进行分析，给出水下彩色图像的初步处理成果并与多尺度Retinex 算法（MSR 算法）［9］、带色彩恢复的MSR 算法（MSRCR 算法）［6］进行比较，本实验软件平台为MatlabR2018b。

3.1 实验结果对比

下面的图7～9 是经过MSR 算法、MSRCR 算法和本文所提算法对水下人与铜像、水下鱼群1 和2的处理结果。

图7（b）、7（c）分别经过MSR 算法、MSRCR 算法及进行处理。 图7（b）和原图相比，消除了原图严重的偏绿色失真，但是对比度不高，而且图中目标也不清晰；图7（c）和原图相比，也对原图严重的色彩失真进行了抑制，效果比图7（b）稍好，但是仍然存在对比度低、目标不清晰问题；图7（d）是经过本文所提算法处理的结果，与7（b）、7（c）相比，人和铜像看起来更加清晰，图像整体亮度更高、对比度也大幅提升，噪声也得到了有效的抑制，图像色彩也更加丰富了。

图8 中MSR 算法处理的结果虽然消除了原图的偏蓝色失真，但是引入了新的颜色失真，图像整体偏暗；经MSRCR 算法处理的结果，虽然鱼的形态清晰一些，但图像整体还是偏暗，而且图像颜色也出现了新的色彩失真；经本文算法处理的图7（d），鱼的形态很容易和背景分离，图像整体对比度和清晰度高，色彩也更加正常。

图9 中，经过MSR、MSRCR 算法处理的图7（b）、7（c）消除了原图7（a）的颜色失真，但是整幅图存在对比度不高、模糊问题；相反，本文算法处理的图7（d）整体对比度更高、图像更加平滑，可以轻易区别鱼和背景，颜色也更加鲜艳。 总之，直观感觉本文算法要优于MSR、MSRCR 算法的表现。

图7 水下人与铜像Fig. 7 Underwater man and bronze statue

图8 水下鱼群1Fig. 8 Underwater fish group 1

图9 水下鱼群2Fig. 9 Underwater fish group 2

3.2 实验数据对比

为了进一步说明实验结果，本文选择信息熵、对比度［10］、均方差、峰值信噪比［11］4 个指标对图像增强效果进行评价。

峰值信噪比PSNR（peak signal-to-noise ratio）即峰值信号与噪声信号的平均能量之比，是衡量图像质量的重要指标之一。 要计算PSNR 必须先计算MSE（均方误差），MSE 是一种常见的损失函数。 设两幅m × n 的单色图像I 和K，若一个为另外一个近似噪声，则它们的的均方误差可以定义为：

其中，MAXI表示图像颜色的最大灰度值，其值最大为255。 由式（12）、（13） 可得MSE 越小，PSNR越大，而且PSNR 越大，代表着图像质量越好。

图像熵是图像特征统计的一种数学表示，它体现出图像平均信息量的大小。 图像的一维熵定义是：图像中灰度分布特征聚集信息量的多少， 用pi表示图像中灰度值为i 的像素所占图像总像素的比例，则灰度图像的一元熵定义为：

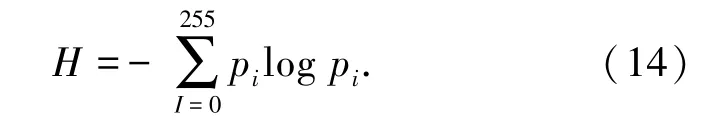
其中，pi是某个灰度在该图像中出现的概率，可由灰度直方图获得。

对比度就是图像黑与白的比值，即图像从黑到白的渐变等级。 对比度越大，图像从黑到白的渐变层次就越多，故表现出的色彩越丰富。

对比度的计算公式如下：

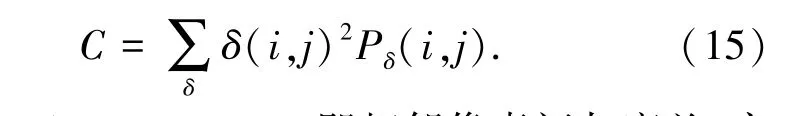
其中，δ（i，j）＝｜i -j ｜，即相邻像素间灰度差，实际实现中取四近邻或八近邻灰度差；Pδ（i - j） 为相邻像素间灰度差为δ 的像素分布概率。 综上，处理后的最佳图像应该具有高熵值、高对比度、低均方误差和高信噪比。

上面是4 种评价指标的理论陈述，4 种评价指标的结果如表1 所示。

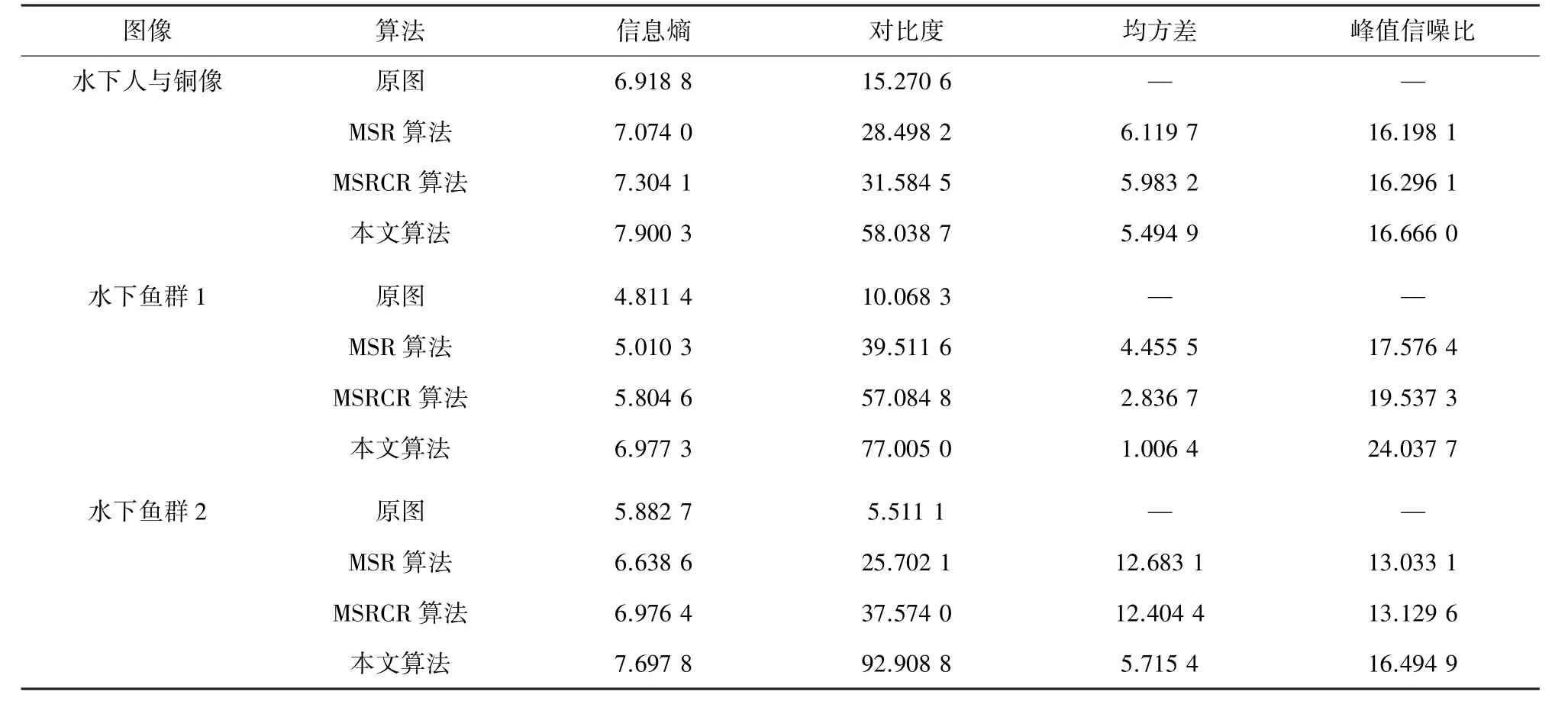
表1 水下图像增强实验数据Tab. 1 Experimental data of underwater image enhancement

如表1 所示，本文算法处理后的图像：信息熵最大，说明算法对原图细节信息具有最好的保留效果；对比度最高，本文算法有效改善了原水下图像的低对比度和低清晰度；峰值信噪比最高，说明了水下图像经本文算法处理后有效信息最多以及对噪声信号进行了最大的抑制。 总而言之，本文算法无论从直观结果还是从客观数据上，对水下彩色图像处理的效果都优于MSR 和MSRCR 算法。

4 结束语

Retinex 理论自问世以来普遍用于图像去雾增强，后来又发展出多尺度视网膜算法（MSR）和带色彩恢复视网膜算法（MSRCR）等。 本文基于MSRCR算法提出了新的水下图像增强方法，所提算法中直方图拉伸将MSRCR 预处理图像的灰度图进行了扩展，而不是仅局限于中间范围，使图像层次分明；伽马变换使得直方图拉伸后图像的对比度和亮度得到增强；最后，虽然引导滤波和双边滤波具有相似保边功能，但是引导滤波可以大大降低运算时间复杂度以及降低计算机运行时间而最终被选择，经滤波处理的最终图像整体更加平滑。

本文算法处理的水下图像对比度和清晰度上都有很大提高、图像色彩失真得到最大的消除以及对原图的噪声进行了显著抑制，提高了图像质量。当然本文算法仍有提高之处，接下来的工作中我会在本文算法基础上就进一步恢复水下目标绚丽颜色的方向做进一步的探索和努力。