基于粒子群方法的转子-支承系统临界转速振动性能优化

杨 璇 白宇杰 吴庭苇

（核工业理化工程研究院，中国 天津300180）

0 引言

旋转机械（如储能飞轮）升速至工作状态的过程中一般会经过系统临界转速，临界转速时转子的振幅急剧增大，可能会超过结构的间隙限值。因此，提高转子的过临界性能对旋转机械具有重要工程意义，一般通过调整其支承参数来实现过临界性能的优化。

本文研究的旋转机械模型为刚性转子-支承系统简化模型。对转子系统的过临界性能进行优化的传统方法是试凑法或者依靠从业人员的工程经验选取，但这些方法往往效率不高且难以得到令人满意的结果。

为提高优化转子系统过临界性能的效率和效果，对相关优化算法进行调研，考虑到粒子群优化算法具有参数较少、易于实现的优点，并且在许多的优化问题中，该优化算法均取得了良好的优化效果，本文采用了粒子群优化算法开展优化工作[1-3]。

通过对振动方程进行分析，明确了最小模态阻尼比可用于描述刚性转子-支承系统的过临界性能。因此，本文采用粒子群优化算法，以模态阻尼比作为优化目标提出了转子-支承系统的单目标优化问题，并参考工程参数的可行性给出参数优化方案。

1 优化模型

刚性转子-支承系统由转子和左、右支承组成，系统的简化模型如图1所示。

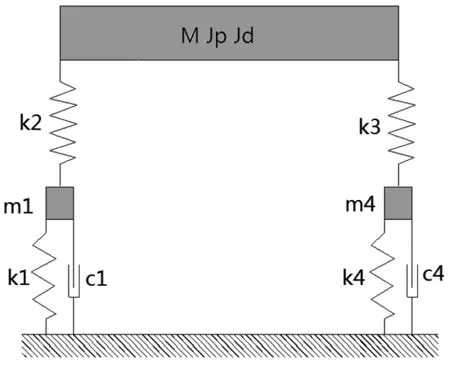
图1 刚性转子—支承系统动力学简化模型

参考实际工作情况，不考虑转子的转子横向位移和所受重力，将转子简化为具有质量M；长度为L，半径为r，以角速度ω旋转，极转动惯量和赤道转动惯量分别为Jp、Jd；左右两端的不平衡质量分别为Δm1和Δm2的刚性体。

转子-支承系统两端的支承对称，由弹簧和阻尼器组成，阻尼器具有质量、刚度和阻尼系数。

由图1可知，刚性转子-支承系统的运动方程如下：

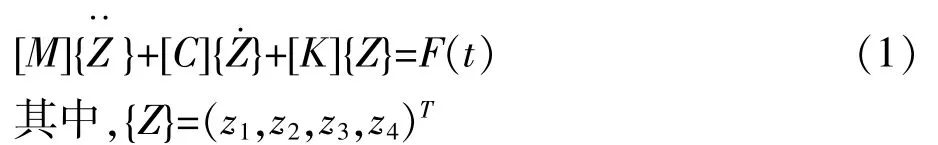
2 优化目标

对于运动方程（1），考虑转子-支承系统的过临界性能。此时，系统为强迫振动，转子的不平衡质量提供外力，即由此得到系统运动方程的解，解的第一项为自由振动，第二项为强迫振动。

式中，{B}——转子-支承系统强迫振动的振幅；

φ——转子-支承系统强迫振动的相位。

{B}的表达式为：

式中，{ε}——转子-支承系统的偏心距。

转子-支承系统过临界时，ω=ωj，此时有：

因为转子的不平衡质量为定值，即转子-支承系统的偏心距为定值。过临界时转子-支承系统的强迫振动振幅与阻尼比成反比关系——阻尼比越大，振幅越小。因此，可以用最小模态阻尼比为目标优化转子-支承系统的过临界性能：当转速为临界转速时，使系统各阶模态中的最小模态阻尼比取得最大值。

3 粒子群优化算法

粒子群优化算法是一种生物群体智能理论优化算法，基本思想是模拟群鸟捕食的自然现象，采用无质量、无体积的粒子模拟鸟类，并扩展到n维空间，粒子i的空间位置采用矢量Xi=[x1，x2，…，xn]T表示，飞行速度采用矢量Vi=[v1，v2，…，vn]T表示。每个粒子都有一个由目标函数决定的适应值，通过跟踪自己到目前为止发现的最优值（Pbest）、相应的空间位置和群体中所有粒子发现的最优值（Gbest），粒子调整自己的空间位置和速度，确定下一步运动。

粒子群优化算法首先初始化一群随机粒子（随机解），采用上述迭代思路找到最优解。在每一次的迭代中，粒子通过跟踪两个最优值来更新空间位置和速度，更新公式如（5）所示。

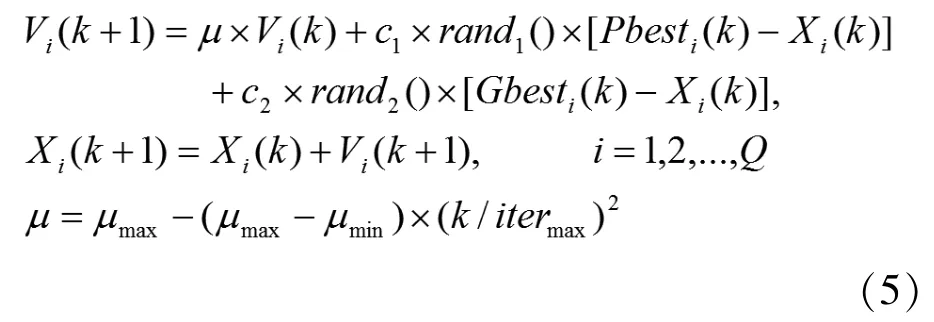
其中，Q是粒子总数；rand1（）和rand2（）是随机数（0～1之间）；c是学习因子；μ是惯性权重，itermax为迭代次数。具体参数如下表1所示。

表1 优化算法参数设定

由方程（1）可以得到8个模态阻尼比ζj，它们分别对应系统的一、二阶模态；一、二阶反模态和阻尼器偏摆的正、反模态。本文针对系统的一、二阶正模态进行优化。采用粒子群算法对提出的单目标优化问题进行求解，系统部分参数如下：M=30 kg；Jd/L^2=2.5 kg；Jp/L^2=1 kg；ω=100 rad/s。

经过3次独立求解，获得的结果稳定一致，收敛曲线如图2所示。对应的一阶、二阶模态阻尼比和系统参数如表2所示。

由表2可知，采用粒子群优化后，转子-支承系统的一阶、二阶最小模态阻尼比均有明显的增大，优化后的最小模态阻尼比是优化前的220%，系统的过临界性能得到了明显的提高。

4 结论

由刚性转子-支承系统运动方程的分析可知，最小模态阻尼比可表征转子-系统的过临界性能，通过提高最小模态阻尼比可实现过临界性能的优化。本文提出了一种基于粒子群优化算法的转子-支承系统过临界性能优化方案，仿真结果表明该方案可增大最小模态阻尼比至优化前的220%，过临界性能取得了有效提高。

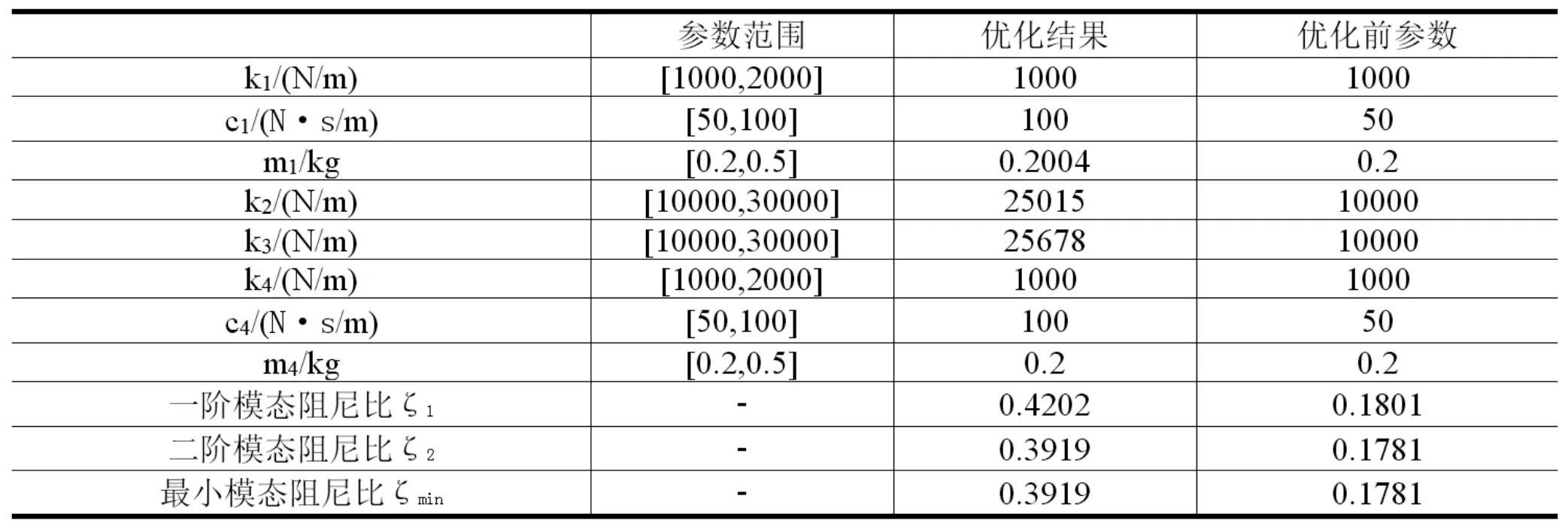
表2 针对过临界性能的转子-支承参数优化结果

图2 转子-支承系统过临界性能优化