MI和改进PCA的降维算法在股价预测中的应用

谢心蕊，雷秀仁，赵 岩

1.华南理工大学 数学学院 信息与计算科学系，广州 510640

2.华南理工大学 数学学院 统计与金融数学系，广州 510640

1 引言

随着信息时代的到来，数据的获取更加便捷，不论是在维度上或样本数目上都呈现爆炸性的增长。由于高维样本数据可能带有噪声信息、冗余信息、不相关信息等特点，容易造成后续的学习算法速度慢、效果差，计算复杂度高等问题[1]。恰当地利用降维算法能够消除噪声，以及不相关和冗余的特征，从而提升学习模型的泛化能力。降维算法主要包括两大类：特征选择和特征提取。特征选择通常是从原始特征集X={x1,x2,…,xn} 挑选出一个真子集X′={x1,x2,…,xm} ，满足m ＜n，其中n是原始特征集的大小，而m是选择以后特征集的大小[2]。此类特征选择方法常用的如互信息（Mutual Information，MI）[3-5]、灰色关联分析（Grey Relational Analysis，GRA）[6]、随机森林（Random Forest，RF）[7]、遗传算法（Genetic Algorithm，GA）[8]等。而特征提取通常适用于原特征集无法生成一个对数据内容进行最优描述的特征空间的情况，所以特征提取通过变换原特征空间，生成一个维数更低、各维之间关联度更低的新特征空间，这类特征提取算法常用的如主成分分析（Principal Component Analysis，PCA）[9-10]、独立成分分析（Independent Component Analysis，ICA）[11]、线性判别分析（Linear Discriminant Analysis，LDA）[12-13]等线性方法。

主成分分析方法是目前应用较广的特征提取方法，意在于消除特征之间的多重共线性，通过将原特征集所在的特征空间变换到新的主成分空间，新的特征即为每一个主成分。在计算完原数据集的协方差阵、相关系数阵或互信息阵的特征值后，通常会用累积方差贡献率大于某一个阈值（通常为85%[14]）的方法来确定需保留的主成分个数，这种方法简单且容易操作，能够保留大多数原始信息，但却不能较好地从相关性方面揭示主成分空间的信息存量，主观性较大。互信息来源于信息论中熵的概念，可以用来衡量两个随机变量的相互依赖度，它对样本的分布类型要求较低，对特征之间的非线性关系能够有效地捕捉，非常适用于有监督的多元数据特征选择问题。

针对有监督任务的特征选择任务，同时考虑特征与标签相关度和特征之间冗余度的问题，以及PCA 单纯用累积方差贡献率确定主元数主观性较大的问题，提出一种基于互信息和改进PCA的双重降维算法。首先利用互信息方法过滤掉一部分与标签关联度过低的特征，再利用累积方差贡献率与复相关系数共同确定主元个数的PCA 方法对剩余的特征进行提取，这样不仅保证了特征相关度、消除了特征冗余度，还提高了主元模型的精度。通过股票数据的实例分析，验证了此方法的有效性。

2 特征选择和提取

2.1 互信息原理

互信息通常用于度量两个随机变量的关联程度，不同于相关系数仅能对两个随机变量的线性相关性进行捕捉，互信息可以捕捉两个变量之间的任何统计依赖性，互信息值越大，则两者共享的信息就越多，关联程度就越高。当进行特征选择时，分别计算各个特征与标签之间的互信息值，选出互信息值大于事先设定的某一阈值的自变量，即可初步筛选出对因变量提供信息量较多的特征子集。

两个离散型随机变量X和Y的互信息定义为：

其中，p(ξ,η)是Y和X的联合概率分布函数，p(ξ)和p(η)分别是X和Y的边缘概率分布函数，式（1）适用于学习器为分类模型的情形。当学习器为回归模型时，即在X和Y为连续型随机变量时，只需将求和号替换成积分号即可：

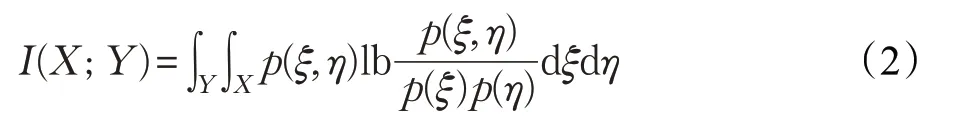
2.2 PCA原理及改进

2.2.1 PCA原理

主成分分析是一种经典的线性降维算法，具有消除特征之间存在信息冗余问题的强大功能，能为后续学习器的学习效果奠定良好的数据基础。假定原始数据集共包含n个样本和m个特征，记为X=(x1,x2,…,xn)T。PCA 旨在找到一组标准正交的基向量pi(i=1,2,…,k)，当X通过这组正交基投影为新数据集T后，T的特征之间两两不相关，并且提取的这前k个主元应包含原始数据集X的绝大部分信息，用式子表示如下[15]：

其中，pi(i=1,2,…,k)即是协方差矩阵的特征值对应的特征向量，且满足λ1＞λ2＞…＞λk,ti(i=1,2,…,k)∈Rn为变换后的新特征，称为主成分或主元。主元个数k的选取至关重要，若k值选取过大，可能会包含太多噪声信息进来，但k值若选取过小，又会容易丢失重要的信息，这两种情况都会使得最终的预测误差增大。一种常用的确定主元个数的方法有累积方差贡献率（Cumulative Percent Variance，CPV）准则：

式（4）为t1,t2,…,tk这k个主成分的累积贡献率，CPV值的大小表明t1,t2,…,tk综合m个原始变量的能力，反应了主元模型的精度，此准则通常取CPV≥85%时的k值作为主元个数，从而保证主元模型的精度能达到进行PCA分析的标准。

2.2.2 PCA主元选取方法的改进（Improve Principal Component Analysis，IPCA）

单一的CPV 方法确定主元个数具有较大的主观性，且不能较好地反映选取的部分主元与原始特征的相关程度，复相关系数（Multi-Correlation Coefficient，MCC）是反映单个变量s与多个变量t1,t2,…,tk相关程度的指标，具体过程为[16]：

（1）用s对t1,t2,…,tk做线性回归，得到：

（2）计算简单相关系数：

式（5）则为s与t1,t2,…,tk间的复相关系数。

设T=[t1,t2,…,tk]T为主成分得分矩阵，原始数据集X∈Rn×m中每个特征表示为sj∈Rn(j=1,2,…,m)。MCC反映了主元与原始变量的相关程度，随着主元个数k的增加，原变量与k个主元的复相关系数也在逐步递增至1，取MCC值大于0.85保证这一强相关性进而确定此时的主元个数。复相关系数能较好地从相关性方面揭示主元空间中的信息存量，而取CPV大于85%是基于方差贡献方面来保证足够的主元信息，两者相辅相成，均需满足。综合两种主元选取方法对单一使用累积贡献率的PCA方法进行改进，则改进的PCA算法步骤如下：

步骤1将原始数据阵X进行中心化和标准化处理，计算协方差矩阵的特征值，并从小到大排列。

步骤2计算累积方差贡献率，并选出累积方差贡献率恰好大于85%时的特征值个数作为主元个数，用k1表示。

步骤3分别计算当主元个数为k1 至m时，每个原始特征与成分得分矩阵的复相关系数，以及平均复相关系数，最终得到m-k1 维数组mcc。

步骤4逐个验证数组mcc从第1 至第m-k1 个数的大小，记恰好大于0.85时的相关系数的索引为k2。

步骤5记最终的主元数k=k1+k2，既保证了85%以上的累积方差贡献率，也保证了原始数据与主元阵相关系数为0.85以上的强相关性。

2.3 互信息和改进的主成分分析融合的特征选择算法（MI-IPCA）

由上述介绍可知，互信息可以帮助人们选择出与标签关联程度较高的特征，而主成分分析方法可以帮助人们消除特征之间的多重共线性，其中改进后的PCA 方法更能准确、多方位地保证主元模型的精度，于是本文提出MI与改进的PCA相融合的双重特征选择算法，此算法会事先设定互信息的阈值δ，先做初步的筛选，将那些与标签关联程度低的特征先舍去，再利用PCA 进行二次降维，消除特征之间的多重共线性。后续将还会利用神经网络对股票实例进行预测。

双重特征选择算法流程图如图1所示。

3 BP（Back Propagation）神经网络预测

BP 网 络 是 1986 年 由 Rumelhart 和 McCelland 为 首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一[17]。BP 网络将真实值与网络输出值的误差逆向传播，通过梯度下降算法来调整各连接权值从而确定最终模型，三层的BP网络结构如图2。

图2 三层BP网络结构

算法大致步骤如下：

步骤1网络初始化，分别赋予各连接权一个（-1，1）区间的随机数，给定误差函数e、最大学习次数M，和精度值ε，给定n个学习样本。

步骤2随机选取第k个样本输入及相应的期望输出：分别为输入和输出层神经元个数。

2.4 播种前1～2天用食用豆油与玉米种子，按1∶100 比例拌种，即：1 两豆油拌10斤种子。具有增温、保温、补充有机营养的功效，可有效的抵御春季土壤温度变幅大，对玉米扎根出苗造成不良影响，利于苗齐苗壮、叶色油绿。

步骤3计算隐藏层和输出层各神经元的输入和输出，记输出层实际输出为。

步骤4利用网络的实际输出Ok和期望输出Yk，计算误差函数e对输出层各神经元的偏导数。

步骤5利用输出层的、隐藏层的输出及隐藏层到输出层的连接权计算误差函数对隐藏层各神经元的偏导数。

步骤6利用输出层的和隐藏层各神经元的输出来调整权值。

步骤7利用隐藏层和输入层各神经元的输入来调整权值。

步骤9判断网络误差是否达到预先设定的最大学习次数M或精度ε，若达到则结束算法。否则，继续随机选取下一个学习样本和对应期望输出，返回步骤3，进入下一轮学习。

4 个股预测案例

4.1 数据准备

本文选取一支指数以及分别属于金融、电子信息两个不同行业的股票数据进行测试。其中指数数据为sz399001（深证成指）1999年6月4日至2019年6月5日的日线数据，样本数目共计4 848 条，股票数据一支为sh600601（方正科技）1999年8月3日至2019年6月5日的日线数据，样本数目共计4 742条，另一支为SZ000001（平安银行）1999 年 7 月 20 日至 2019 年 5 月9 日的日线数据，样本数目共计4 635条。

选取次日收盘价作为因变量，所选指数因变量不仅包含当日开盘价、收盘价、最高价、最低价、成交额、成交量、次日开盘价共7 个行情指标，还包括情绪指标中威廉变异离散量WVAD、意愿指标BR、6 日均幅指标ATR6、12 日量变动速率指标 VROC12、成交量的 10 日指数移动平均VEMA10，以及随机抽取的alpha101因子中的alpha_003、alpha_015、alpha_022、alpha_033、alpha_054，共计17个指标。两支股票所选自变量不仅包括上述7个行情指标，还包含市值、换手率、市净率PB、市现率PC、市盈率PE、市销率PS共6个市值指标，还包括21日移动平均MA21、平滑移动平均MACD、20 日收盘价标准差20SD、指数移动平均EMA共4个技术指标，共计17个指标；较大范围地考虑了影响股价或指数变动的因素。本文采用均方误差（MSE）作为后续神经网络预测器的评价指标，MSE的计算公式如下：

其中，yi和分别为真实值与网络输出值，n为样本个数。

4.2 实验过程及结果分析

实验共分为三大部分，一是数据归一化，二是特征选择，三是神经网络预测。首先数据按照式（7）进行归一化操作，转换到[0，1]的范围：

4.2.1 利用互信息和改进PCA进行降维

利用互信息选择变量的方法进行第一次特征筛选，计算出两支股票以及一支指数17个变量分别与标签之间的互信息值如图3所示。

图3 变量与标签的互信息值

互信息值的大小范围为[0，1]之间，这里将其划分为三个程度认为是弱相关，认为是中等相关认为是强相关。由图1 可以看出只有极少数几个特征的互信息值处于弱相关水平，此处设定阈值δ大小为，将少数几个互信息值低于的特征过滤掉，认为是对标签信息量贡献较低的特征。最终过滤后两支股票得到剩余13 个变量，以及一支指数得到剩余10个变量。

然后利用改进的PCA方法对上述股票剩余的13个变量以及指数剩余的10个变量进行二次降维。当利用累积贡献率和复相关系数法方法确定主元数时，CPV值与平均复相关系数值在前6个主成分的变化如表1和图4所示。

表1 主元数为1～6时的CPV值及平均复相关系数

图4 主元数为1～6时的CPV值及平均复相关系数

由表1 可以看出，当主元个数为2 时，平安银行的CPV 指标的值为0.849 7，大约已达到85%，方正科技的CPV指标为0.929 2，已超85%，基本满足了进行PCA分析的要求。此时平安银行的平均复相关系数仅仅达到了0.827 3，还未满足事先设定大小为0.85 的阈值，若仅此决定取2个主元，可能会丢失部分重要的原始信息，而此时方正科技的平均复相关系数为0.898 3，已超过0.85。

当主元个数为3时，平安银行和方正科技的CPV值已经分别达到0.922 3 和0.958 8，平均复相关系数的值也分别达到0.873 6 和0.943 0，均超过0.85。此时无论从方差贡献或者是相关性方面去衡量主元阵，主元阵都已包含了原始数据的绝大部分信息。但相比于2 个主元的情况，方正科技尽管有更高的CPV 值和平均复相关系数，却已增长较少。

当主元个数为4时，平安银行CPV的值为0.947 8，尽管此时CPV和平均复相关系数拥有更高的值，但是相对于3个主元的情况，CPV的值仅增加了0.025 5，变化极少。

同时结合图4分析，当主元个数为1～3时，平安银行的CPV 指标与平均复相关系数的值增长得较快，而主元数超过3 时，变化就趋于平缓，所以认为平安银行的最优主元数为3。而方正科技在主元数为1～2时增长较快，且CPV 与平均复相关系数在主元数为2 时都超过0.85，而之后CPV 值的变化极少，所以认为方正科技的最优主元数为2。

深证成指在主元数为1 时，CPV 的值就已经高达86%，而此时平均复相关系数的值仅为0.704 7，还未达到0.85，当主元个数为2时平均复相关系数才超过0.85，此时CPV 的值已经达到了0.97，之后增长迅速减缓，所以最终确定最优主元个数为2。

4.2.2 神经网络预测

考虑到股票数据集的实际意义，总是用历史数据去预测未来数据，所以将上述归一化及降维后的数据按时间序列排列后，取前80%作为训练集，共计3 708 条数据，剩余后的20%作为测试集，共计927条数据，构建三层的神经网络，隐藏层节点按经验公式（8）设定：

h为隐层节点个数，n为输入层节点个数，m为输出层节点个数，a为0～10之间的调节常数。

设置最大迭代次数为5 000次，最终预测结果如表2和图5、6所示。

图5 主元数为1～6时的神经网络预测均方误差

如表2和图5所示，利用神经网络进行预测后，深证成指和方正科技的MSE在主元数为2时达到了最小，而平安银行的均方误差MSE 在主元数为3 时达到了最小。虽然平安银行在主元数为4～6 时MSE 仍然处于较低值，但却不是使数据达到最精简的主元数，而方正科技和深证成指在MSE达到最低值后又有缓缓上升的趋势，再一次验证了利用CPV和mcc共同确定主元数的客观性和合理性。

由图6 可看出，当按上述方法取最佳主元个数时，预测值曲线与真实值曲线大致拟合，此时深证成指、方正科技、平安银行的MSE 的值分别为0.000 383 9、0.000 178 7、0.000 224 9。为了说明互信息筛选的有效性，图7为不利用互信息进行第一重特征筛选，而直接利用改进后的PCA降维的BP预测结果，此时平安银行的MSE值为0.000 475 5，明显高于前者MSE的值0.000 224 9，而方正科技和深证成指的MSE 分别为0.000 190 6、0.000 426 5，也都略高于前者MSE 的值0.000 178 7、0.000 383 9，说明先利用互信息挑选再进行PCA 降维，可以使预测结果更加准确。

表2 主元数为1～6时的神经网络预测均方误差（MSE）

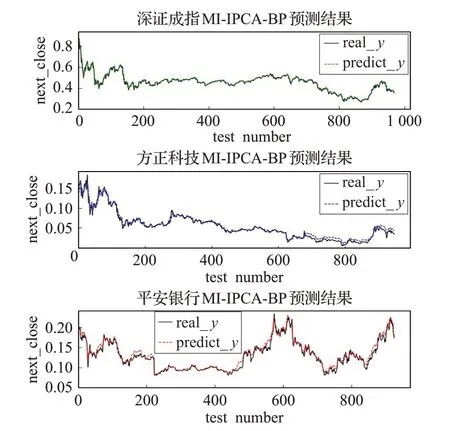
图6 主元数最佳时的MI-PCA和BP预测结果

图7 仅用IPCA和BP的预测结果

5 结束语

利用互信息和改进的PCA相结合共同提取特征的降维算法，不仅保证了在初步筛选时将不相关的特征舍去，仅留下与因变量关联程度较高的特征，还利用了CPV和MCC共同确定主元数的方法对PCA进行改进，从方差贡献及相关性两方面进行考虑，保证主元阵重要信息容量的同时也避免了多余噪声的加入，与后续预测过程紧密结合。通过上述神经网络对个股的预测结果可以说明，此双重降维算法具有一定的有效性和可实践性。