图正则化非负矩阵分解的异质网社区发现

刘家骥，包崇明，周丽华，王崇云，孔 兵

1.云南大学 信息学院，昆明 650091

2.云南大学 软件学院，昆明 650091

3.云南大学 生态学与环境学院，昆明 650091

1 引言

现实世界中，许多复杂的系统都可以抽象成网络的形式，对于复杂网络的研究能够加深对于不同系统性质的了解。目前，针对同质节点网络有比较深入的研究，如社区发现[1]、影响最大化[2]和网络传播[3]等。然而，现实世界网络往往由多种不同类型的异质节点构成，异质节点间的交互往往代表不同的连接关系。在实际网络中，多种类型的节点由多种类型的链路连接，从而形成异质信息网络（Heterogeneous Information Networks，HIN）[4]。例如，从论文合作网络[5]中提取的数据包含作者、论文、关键词和会议等多类型对象。这些不同类型的对象之间形成了不同类型的连接关系。

异质网络数据挖掘的关键研究问题之一是社区发现[1]（community detection）。社区发现即根据网络包含的链接、内容等大量属性信息，对网络中具有共同属性的潜在结构进行挖掘。挖掘异质网络中有用的、具有稳定性的社区，同样具有重要的研究价值。同质网络[6]将社区定义为：网络中具有某种相似特性的节点集合，社区内部节点联系紧密而社区间联系相对稀疏。推广到异质网络，可以认为：社区内部各种相同或不同类型节点间的连接紧密，而社区间的各种相同或不同类型节点间的连接则比较稀疏。但在异质网络社区发现中，异质网络中的异构性导致以下两个问题[7]：（1）异质网络中互动噪声很多，引起算法的性能降低。网络中节点的属性可以看作是连接到节点的所有边相互作用和叠加的结果，一些不重要的信息往往能够给聚类带来很大影响，这就是异质网络中大量存在的噪音。（2）各个异质节点关系错综复杂，难以在同一维度中有效整合网络中的异质信息，挖掘出符合实际的社区结构。将多维的异质网络转换成同质网络是当前针对异质网络聚类的主流方法，但是在降维的过程中如何最大限度保留异质信息以及在同一维度有效整合异质信息，是当前所面临的一大挑战。

针对异质网络社区发现存在的难点，研究人员进行了很多尝试。主题模型是对网络中蕴藏的语义信息进行统一建模的方法，代表性的有潜在语义分析（LSA）[8]、概率潜在语义分析（PLSA）[9]和潜在狄利克雷分配（LDA）[10]等模型，它们能够有效地对异质网络中的社区结构进行挖掘。Deng等人[11]提出TMGP算法，将异质网络中的不同节点信息集成到主题模型中，初步完成对社区的有效划分，不过多数的主题模型，都仅仅单纯地利用了文本集中的语义信息，而语义信息在一定程度上并不能很好地代表社区结构的特征，且必须满足异质节点相互独立的条件，有一定的局限性。

最近研究发现，将排序算法和聚类算法组合到一起，能产生一定的“化学反应”，从而达到令人较为满意的研究结果。RankClus[12]是基于排序的经典聚类方法，先对目标对象进行排序，由排序结果决定聚类对象向量，通过迭代对目标对象类别进行调整，可以得到较为准确的聚类效果。基于排序和聚类相结合的方法虽然充分考虑了异质链接关系的信息，但是都没有考虑同类型节点之间的交互关系。

异质网络中节点复杂多样，呈高维态势，因此通过降维完成异质网络到同质网络或者二分网络的转换也是目前一种常用而有效的方法。常用的降维方法包括主成分分析（PCA）[13]、线性降维分析（LDA）[14]、非负矩阵分解（NMF）[15]等。当前大部分相关算法并不能很好地去除异质节点之间噪声，在网络转化过程中会丢失大量网络信息，同时无法在同一维度对网络信息进行有效整合[16]。而非负矩阵分解已经被证明了能够很好地保持网络原始信息，且方法简单明了、解释性强、效率高。如何将NMF 应用于异质网络社区发现，是本文研究的重点。

本文以异质网络中的星型网络作为研究对象，提出了一种融合各个子网络异构信息和各个子网络内部拓扑信息的联合优化算法，即基于图正则化非负矩阵分解的异质网社区发现方法。为了将异质信息在同一维度进行有效整合，该算法首先对反映了不同子网络共有潜在结构的共识矩阵进行学习，使用共识矩阵中每个行向量作为中心类型节点在每个社区当中的隶属度分布，通过不断迭代优化系数矩阵和共识矩阵，对两个反映不同类型节点的子空间进行优化，在降维过程中也较大限度地保留了异质信息的完整性。同时，在考虑了不同子网络之间异质关系的基础上，算法结合多重子空间的流形约束，利用图正则化，将中心类型子空间和属性类型子空间的连接关系（即各个子网络内蕴的拓扑结构信息）作为约束项，引入到正则化联合优化算法之中。通过优化法则不断迭代系数矩阵，找到高维数据在低维空间的紧致嵌入，成功消除了异质节点之间的部分噪声。

2 算法思想

非负矩阵分解（NMF）算法具有简便、可解释性强和存储空间少等优点，能够在降维过程中较好地保持信息的完整性。在对异质网络进行聚类时，它最关键的作用是能够有效地揭示异质网络中多维数据潜在的结构特征[17-18]。同时，由于NMF算法中分解得到的矩阵元素都必须满足非负条件，因此该模型几乎满足了所有现实数据的物理属性，可解释性强。与大多数最先进的无监督算法相比，NMF 显然拥有更加具有竞争力的性能。然而，当前鲜有将NMF运用于异质网络聚类的算法，因为直接将NMF 应用于异质网络聚类，需要向其分解因子矩阵U和V同时施加非负正交的约束，约束太强会使矩阵分解的逼近程度大大降低，从而限制了异质网络的聚类性能。另一方面，当前算法无法有效解决去噪问题，也难以在同一维度整合异质信息。本文提出的HINGMF算法，优势主要有以下几个方面：（1）在非负矩阵分解中，通过引入共识矩阵V*，找到不同类型节点之间有意义且具有可比性的因式分解，从而充分利用了异质信息，让其在同一维度得到有效整合；（2）通过图正则化，将中心类型子空间和属性类型子空间的内部连接关系作为约束项引入非负矩阵分解，结合多重子空间的流形约束，有效利用子网络拓扑结构信息，达到去噪效果。

在实际生活中，许多的网络都有一类中心节点，所有的属性节点都通过中心节点相连接。在异质网络中，存在着大量的星型结构网络[18]，多种类型的节点通过同一种中心类型节点联系在一起。图1 所示的论文发表网络即为一种具有星型模式的网络，由关于研究论文的多种信息组成。每篇论文由一组作者撰写，使用一组关键字，并在会议中发布。这样的书目网络由四种类型的对象组成：作者、会议、关键字和论文。论文和作者之间存在“被撰写”和“撰写”之间的关系，论文和术语之间存在“包含”和“被包含”的关系，而论文和会议则存在“被发表”和“发表”的关系。从图1 可看出，书目信息网络呈星形网络模式，其中论文属于中心类型，并且所有其他通过论文链接的对象，都称为属性类型。在书目信息网络中，存在三个子网络，分别是：论文-会议网络、论文-作者网络、论文-会议网络。

图1 星型网络模型

假设有一个由中心类型和T种属性类型之间的二分网络组成的异质网络，用{X(1),…,X(t),…,X(T)}表示所有子图的邻接矩阵，其中X(t)的每一列表示一个中心类型节点而每一行表示一个属性类型节点。对于每一个子网络X(t)∈RM(t)×N，希望找到满足X(t)≈U(t)(V(t))T的低秩因式分解U(t)∈RM(t)×K和V(t)∈RN×K。在这里M(t)是属性类型t的节点个数，N表示中心类型的节点个数，K代表希望发现的聚类个数。HINGMF 将通过U和V共同揭示异质网络中隐藏的社区结构。

3 基于图正则项非负矩阵分解的异质网络聚类方法

和NMF 算法类似，异质网络每个子网络的目标函数为：

||·||F即F范数，U(t)≥0,V(t)≥0 代表对矩阵中每个元素都非负的限制。但是，这种表述假设每个子网都是独立的，并且无法以统一的方式对异质网络建模。通过将从子网络中学到的系数矩阵V(t)与共识矩阵V*之间的差异结合起来，改变目标函数为：

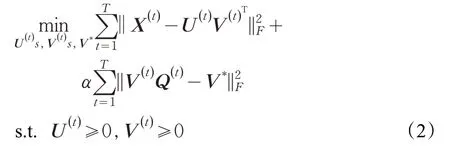
对角矩阵Q(t)定义如下：

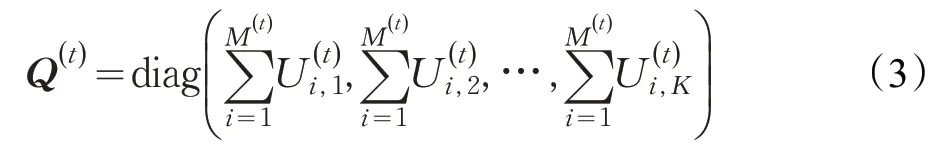
在计算误差之前，将V(t)乘以Q(t)，以确保从不同子网中学习的V(t)具有可比性，在这里||X(t)||1= 1。另外，使用α作为固定参数来调整V(t)和共识矩阵V*差异的权重，文献[19]表明该参数不太敏感，因此在整个实验中将其设置为0.1。

文献[20]表明，重视低维流形的几何信息可以提高聚类质量。根据流形假设[21]，异质网络数据经非负矩阵分解后，同类节点间的局部邻域结构在低维特征空间中能够得以保持，则当高维空间中距离较近的向量Xi·，Xj·映射到对应的低维流形上Vi·，Vj·时，距离依然较小。从而定义基于用户子空间的正则项（平滑度惩罚项）为：

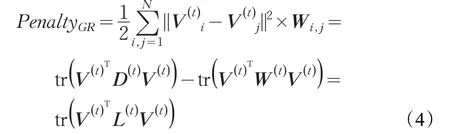
tr(·)表示矩阵的迹，W表示正则项权重矩阵，而矩阵D是满足称为拉普拉斯矩阵。结合之前的模型得到了一个新的模型：

到目前为止，将整个异质网络的所有二分子网络视为同等重要。考虑到不同子网络的相对权重，通过将一组参数β(t)引入方程来开发自动权重学习策略。采用以指数形式表示的相对权重的原因是为了避免完全有利于具有最小误差的子网络，目标函数变为：

RE(t)表示与属性类型t相关的子网络的重建误差：

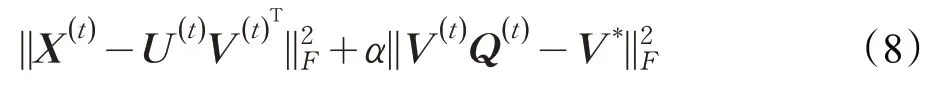
为了解决上述优化问题，提出了一种迭代优化算法，分为以下三个步骤：（1）初始化，（2）固定V*，更新U和V，（3）固定U和V，更新V*。迭代（2）和（3），直到公式（6）收敛。算法1总结了这个两步过程。算法流程图如图2所示。

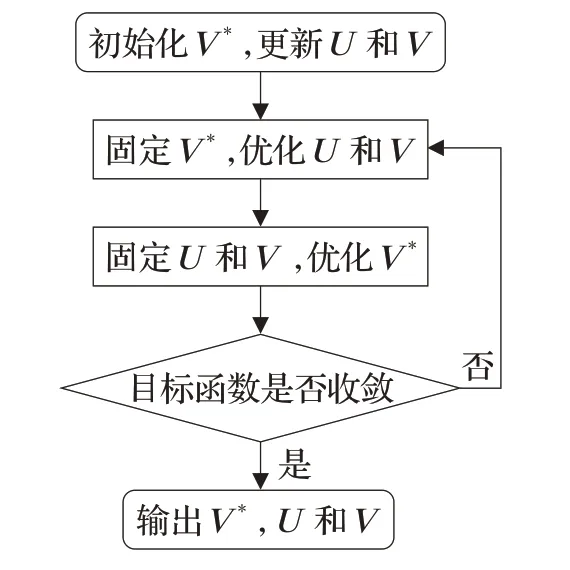
图2 算法流程图

3.1 初始化

基矩阵U(t)和系数矩阵V(t)的合理初始化在HGNMF算法的整体性能中起重要作用。文中使用各个子网络中的几何信息来初始化特定基矩阵和系数矩阵。为实现此目的，每个子网单独进行NMF聚类，单个子网络的优化问题可以简写为：

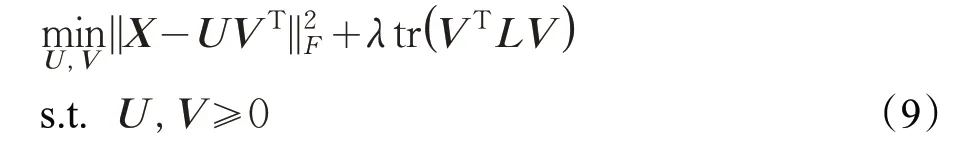
文献[22]提出，可以使用乘法更新过程最小化单独对子网内部的系数矩阵和基矩阵进行优化。注意，此步骤是针对每个子网络独立执行的。则可得到基矩阵和系数矩阵的迭代公式。

图正则项权重矩阵W可定义为：

其中，N(i)为节点i的k-最近邻集合，并采用0-1 加权方式创建k-近邻图的权重矩阵：如果节点i是节点j的k-近邻节点，或者节点j是节点i的k-近邻节点时，Wi,j=1；否则Wi,j=0。

若已知节点i和节点j或节点j和节点i属于同一类，则Wi,j=1，否则Wi,j=0。

得到U和V后，根据之后推导得到的公式（22）初始化V*。

3.2 固定V*，优化U 和V

一旦V*被固定，则每个子网络就可以独立进行优化。对于每个子网络，将损失函数简写如下：

接下来，推导出可用于最小化公式（12）中的优化问题的更新规则。

3.2.1 固定V*和V ，更新U

设ψ为满足限制条件U≥0 的拉格朗日乘子矩阵，则拉格朗日函数L(U,V)=O(U,V)+tr(ψU)。只考虑包含U的项，可以把L(U,V)重新写成：

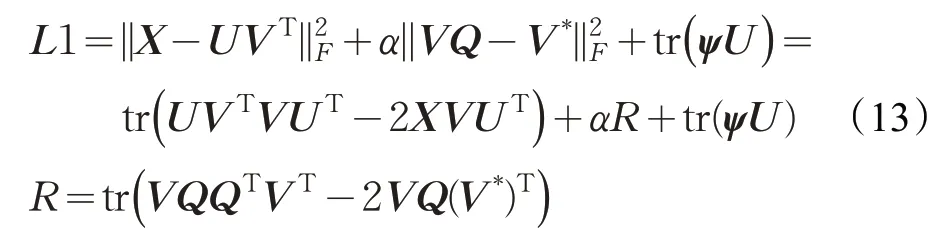
结合式（3）：

R对U进行求导可得：

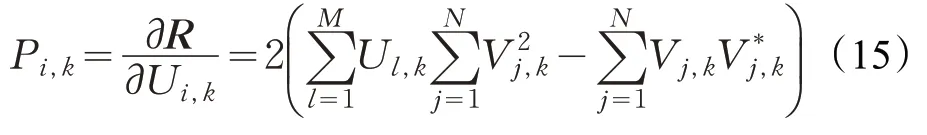
运用KKT（Karush-Kuhn-Tucker）条件可得：

结合以上条件，可得出以下U迭代公式：

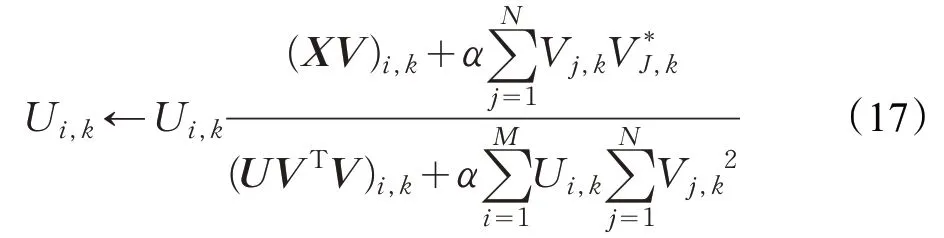
3.2.2 固定V*和U ，更新V

为确保从不同子网中学习的V(t)具有可比性，首先对U的列向量用Q进行正则化：

设Φ为满足限制条件V≥0 的拉格朗日乘子矩阵，则拉格朗日函数：

和之前的步骤一样，可以得到V的迭代公式：

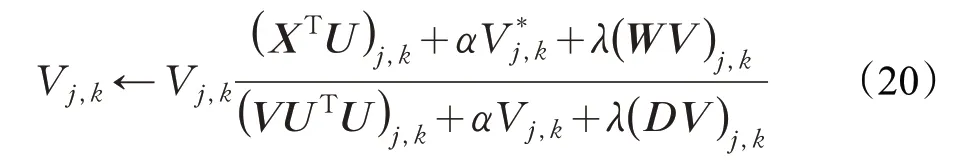
3.3 固定U 和V ，优化V*

损失函数O对V*求导：

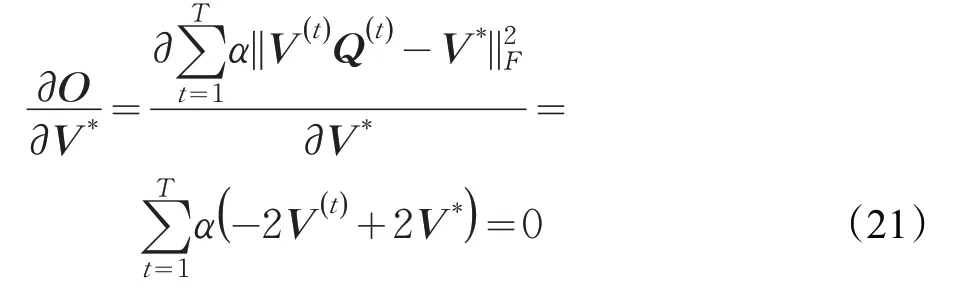
可以得到V*的迭代式为：

算法1基于图正则项非负矩阵分解的异质网络聚类方法

INPUT：HIN{X(1),…,X(t),…,X(T)}，parameters α，number of clusters K

OUTPUT：Clustering on both center type and attribute types

1.Normalize each subnetX(t)such that ||X(t)||1=1

2.InitializeU(t),V(t),V*andβ(t)(1 ≤t≤T)

3.while Eq.6 not converges do

4.for t=1 to T do

5.while Eq.12 not converges do

6.FixingV*,β(t)andV(t),updateU(t)by Eq.17

7.ComputeQ(t)as in Eq.3

8.NormalizeU(t)andV(t)as in Eq.18

9.FixingV*,β(t)andU(t),updateV(t)by Eq.20

10.end while

11.end for

12.FixingU(t)andV(t)(1 ≤t≤T), updateV*andβ(t)by Eqs.22 and 7.

13.end while

14.Cluster nodes of center type indicated by arg maxkVj*,k

15.For each attribute type t，cluster nodes of this type indicated by

3.4 时间复杂度分析

对于每个子网络，内循环的算术运算并不复杂，这与公式（1）中单个子网络NMF 的乘法更新规则非常相似。设M为中心类型节点个数，N为属性节点个数，K为分类个数，T为子网络个数。分步分析算法的复杂度，更新U的时间复杂度为O(MNK+(M+N)K2+(2N+3)K) ，更新V的时间复杂度为O(MNK+(M+N)K2+2NK)，更新共识矩阵V*时间复杂度为O(TMN)，算法的总复杂度为O(TMNK)。

4 实验

4.1 实验数据集

DBLP[5]是计算机领域的英文文献数据库，收录了国际期刊和会议等公开发表的论文。它包含4 023 位作者，20个会议和11 771个关键词，涵盖了人工智能、信息检索、数据挖掘和数据库四个领域。其满足星型结构，可分为三个子网络：论文-会议子网络、论文-作者子网络、论文-会议子网络，中心类型节点为论文节点。

Digg[23]数据集是集合了新闻信息和社交信息的网站，用户可以在该网站上发布、评论新闻，也可以在网站上进行交友活动。Digg 数据集由9 583 个用户，44 005条新闻和8 596个关键字组成，共包含4个兴趣小组：游戏小组、政治小组、体育小组和商业小组。在实验中取其40 000 条数据。其满足星型结构，可分为两个子网络：新闻-用户子网络、新闻-关键字子网络，中心类型节点为新闻节点。

Cora[24]论文引用数据集，该数据集由30 714篇学术论文、20 224 位作者以及17 265 个关键字组成，共包含7个研究领域：案例学习、遗传算法、神经网络、概率方法、增强学习、规则学习、理论研究。数据集中有关键字、作者和论文这三种节点，实验选择论文作为中心类型节点，两个子网络为论文-作者网络和论文-关键字网络。三个网络的主要特征如表1所示。

表1 三个数据集的特征

4.2 度量标准

由于实验选择的数据集社区结构已知，这里采用两种通用的评价指标来衡量各种聚类算法的聚类质量：

聚类准确度（AC）[25]：将预测结果与实际标签做对比。可定义为：

其中，AC为聚类准确率，ci和ci分别为数据点xi的标签与实际标签；δ(i,j) 为 delta 函数，如果i=j，δ(i,j)=1，否则δ(i,j)=0 ；map(·) 为最优映射函数。聚类准确率越高，表明聚类算法的聚类质量越好。

标准互信息（NMI）[26]：为了评价社区发现的有效性，引入标准互信息（NMI）指标。通过对比网络社区结构与算法发现的网络社区结构的相似性验证算法的有效性。NMI 的取值范围为[0，1]，值越大表示划分得到的社区越接近真实网络中的社区结构。NMI定义为：

其中，Ni表示聚类标签与实际标签集中第i类样本的数目 (1 ≤i≤k)，Ni,j为第i个类簇中属于实际的第j类的样本数目。NMI值越大，这说明算法的社区划分质量越好。

4.3 实验结果与分析

为了验证本文提出的 HINGMF 算法的有效性，本文分别在三个常用的异质网络数据集：DBLP 网络、Digg网络、Cora网络上进行了验证，度量标准有聚类准确度和标准互信息，它们都能一定程度地反映算法聚类的效果。之后将其结果与其他三种经典算法进行比较。实验结果表明，HINGMF算法具有较高的精度和效率，聚类效果要明显好于其他常用算法。

4.3.1 图正则项参数λ 的选择

为了分析图正则项参数λ对HINGMF 算法聚类质量的影响，从0至0.3选取9个点，调整参数λ的值，对三个数据集进行测试，分析AC和NMI值的变化情况。结果如图3所示。

从图3中可以看出，当没有任何子网络内部连接信息时，即λ接近0时，算法变为HINMF算法，聚类效果较差。随着λ的增大，各个子网络内部拓扑信息被加入，聚类效果逐渐变好。当λ超过0.1 后，不论在DBLP 数据集、Digg 数据集，还是在Cora 数据集上，由于加入过量的子网络内部连接信息，降低了作为连接所有属性类型节点的中心类型节点在网络结构中的重要性，算法的聚类效果开始下降。所以在后续实验中，图正则项参数λ均设为0.1。

4.3.2 实验结果

为了证明所提方法聚类性能的有效性，与以下算法进行了比较。

NetClus[27]：针对异质网络中大量存在的星型结构网络，进行了排序迭代聚类，利用排序提高聚类的效果，并且划分出具有相同星型结构的社区集合。它是目前针对星型网络比较有效且常用的聚类方法。

NMF-LSE[22]：该算法在非负矩阵分解的基础上，结合空间流形约束加入了图正则项，同样将先验信息融入图正则项权重矩阵，将先验信息与拓扑信息相结合，有效平衡了两者的关系，提高了聚类的性能。

HINMF[28]：异质网络非负矩阵分解算法。该算法针对异质网络中的星型网络，通过实现各个子网中中心类型节点最小化来平衡不同子网络之间的差异，但是没有考虑各个子网内部的拓扑结构，不过依然能够达到比较好的聚类效果。

表2 记录了四种方法在不同数据集中的聚类效果。可以看到，HINGMF 的表现要优于其他算法，因为它通过对不同子网络共有潜在结构的共识矩阵进行学习，充分挖掘并利用了各个子网络之间的关联信息，又引入了图正则项，将中心类型子空间和属性类型子空间的内部连接关系作为约束项，引进到算法中，有效地利用了子网络内部拓扑结构信息，成功整合了不同子网之间关联信息和子网内部几何信息，去除了部分噪声，所以算法在数据集上的效果都比较好。而HINMF 算法，同样考虑了各个子网之间的关联信息，但是并没有考虑各个子图内部节点的几何信息，从而算法精度较低。而NMF-LSE算法在针对同质网络进行聚类时能够有非常好的效果，但是没有考虑星型结构网络的各个子网之间的关联性，所以效果一般。NetClus 算法先对属性类型节点进行排序，再根据中心类型节点确定聚类对象向量，迭代调整中心类型节点类别，进而完成社区划分，但是当数据较多时，排序过程耗费时间比较复杂，且排序并不能让节点精确划分，故其聚类效果与几类算法相比不够理想。

表2 真实数据集中四种算法的性能 %

图3 参数λ 对实验效果的影响

当图正则项权重矩阵中加入先验信息时，实验结果如表3所示。可以看到，加入少许先验信息加入权重矩阵效果要优于采用0-1 加权方式创建的k-近邻图权重矩阵，同时避免了计算k-近邻图，减少了计算量。当添加的先验信息只有2%的时候，其聚类效果已经和权重矩阵为k-近邻图的原算法相当，之后，随着先验信息的增多，其效果远大于原算法。

表3 加入不同比例先验信息的聚类效果 %

四种算法的结果对比如图4所示。可以明显看到，提出的算法在精度和NMI值两个指标上明显要优于其他三个算法。

5 结束语

异质网络中存在多种不同属性的节点和关系信息，迫切需要新的方法应对这种需求。本文提出了一种新的异质网络社区发现方法，该方法在遵循星型异质网络中不同子网络中的数据点将以高概率分配给相同聚类原则的基础上，提出了一种可以融合各个子网络异质信息的联合优化算法，该算法对反映了不同子网络共有潜在结构的共识矩阵进行学习，使用了共识矩阵中每个行向量作为中心类型节点的在每个社区当中的隶属度分布，通过轮流固定系数矩阵和共识矩阵，迭代对两个反映不同类型节点的子空间进行优化，从而成功解决了无法有效整合异质信息的问题。同时在降维过程中较大限度地保留了异质信息的完整性。其次，将正则项引入到优化算法之中，结合多重子空间的流形约束，有效利用了各个子网络的拓扑结构，通过优化法则不断迭代系数矩阵，找到了高维数据在低维空间的紧致嵌入，成功消除了异质节点之间的部分噪声。如何优化算法，使算法适用于大规模网络的分析是本文下一步的研究内容。

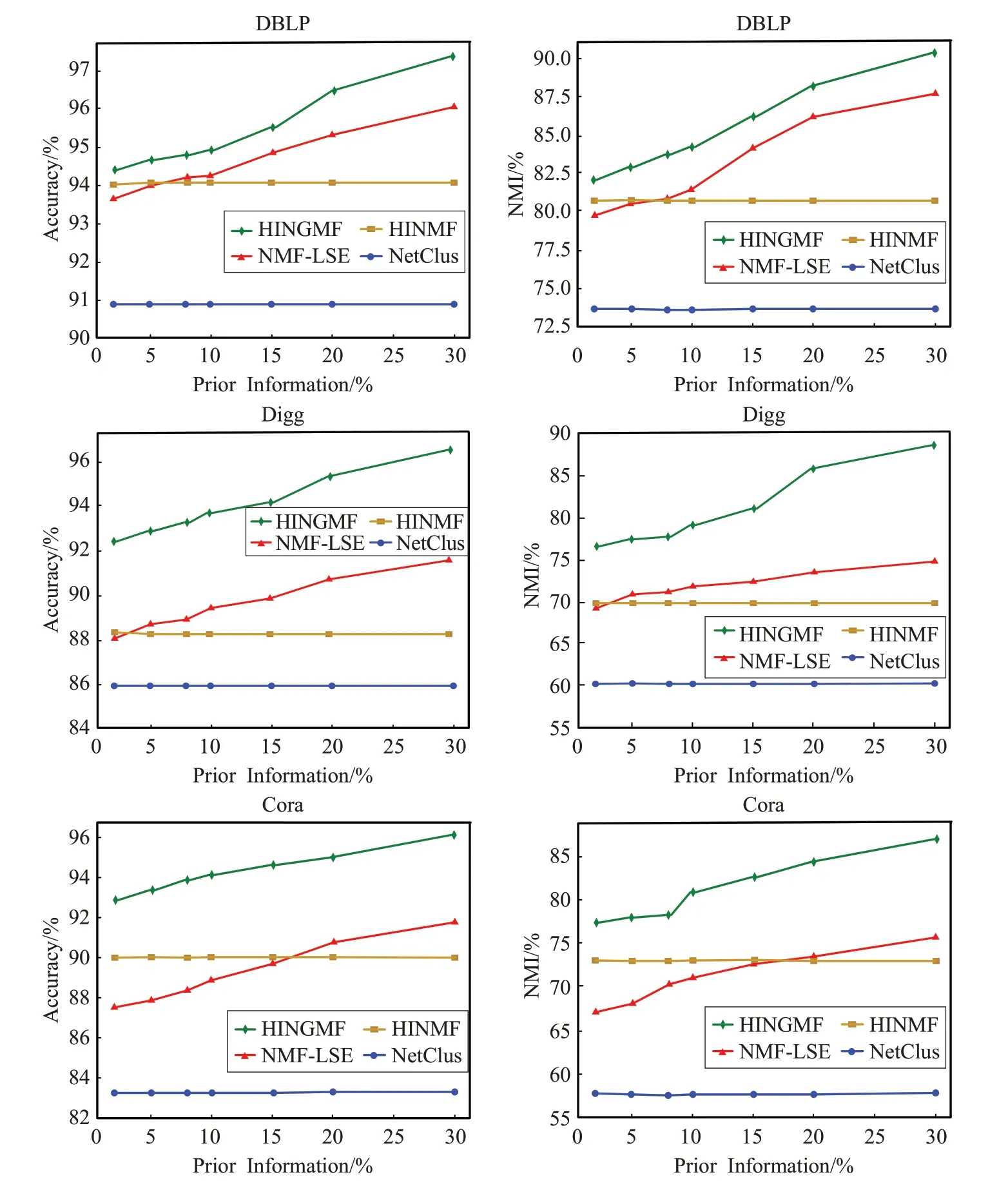
图4 不同算法在不同数据集聚类效果对比