基于概率模型的实时修正IMM目标跟踪算法

周 非 ，罗晓勇 ，刘云萍

1.重庆邮电大学 通信与信息工程学院，重庆 400065

2.光通信与网络重点实验室（重庆邮电大学），重庆 400065

1 引言

无线传感网络由分布在监控区域内的大量传感器节点组成的多跳自组织网络。由于其具有成本低、自组织、快速部署、容错性高等优势，非常适用于战场目标定位[1]、智能交通[2]、海洋监测[3]等应用中。

机动目标跟踪技术是当前无线传感器网络研究的热点之一。该技术利用传感器在网络中广播的信号对目标进行状态估计。现有的自适应跟踪算法主要分为单模型和多模型两类。其中输入估计模型[4]、Jerk模型[5]和CS模型[6-8]属于单模型类自适应跟踪算法。由于目标实际运动形式复杂多变，采用单一模型难以满足跟踪精度的需求。与单模型类自适应跟踪算法不同，多模型类算法采用多个模型来描述目标运动过程中可能的状态，最后通过有效的加权融合进行系统状态估计，很好地克服了单模型估计误差较大的问题。IMM算法在多模型算法的基础上，假定各模型之间的切换服从已知的马尔科夫链，并考虑模型之间的相互作用，得到目标最终的状态估计[9]。近年来IMM 算法的研究工作主要从三个方面展开：一是研究自适应变结构IMM 跟踪算法[10-11]；二是目标运动模型的设计[12]、非线性滤波器的设计及其参数自适应[13]；三是利用后验信息进行Markov 转移概率的实时修正[14-17]。

在IMM算法中，控制子模型间交互和切换的Markov转移概率矩阵通常是根据先验信息设置为固定的主对角占优矩阵。然而，当先验信息不确定时，采用固定Markov转移概率矩阵会造成较大的跟踪误差。针对这个问题，近年来提出模型概率自适应修正的方法，充分利用后验信息对模型转移概率进行实时修正，进而获得较为准确的后验估计，提高跟踪精度。文献[14]首先定义误差压缩率，然后在输出阶段利用误差压缩率比对Markov 转移概率矩阵进行实时估计，在一定程度上提高了模型间的切换速度。文献[15]根据模型似然函数值对Markov 转移概率实时修正，这种方法使模型间的切换更为迅速合理，具有较高的跟踪精度。文献[16]和文献[17]利用两个连续时间点之间模型概率的变化这一后验信息对Markov 转移概率进行自适应调整，一定程度上提高了模型的切换速度。

尽管上述文献提出的模型概率自适应修正的方法在滤波输出阶段可以提高匹配模型的作用，减小非匹配模型的影响。然而，这些方法仅考虑单一模型概率变化，没有考虑模型间交互的情况。此外，当目标机动由非匹配模式转向匹配模式时，以上方法均会产生较大的峰值误差。为解决此问题，本文首先根据IMM 算法输出残差协方差矩阵的理论值和统计值之间的差异，引入模糊神经网络（Fuzzy Neural Network，FNN）对测量噪声协方差矩阵进行动态调整；同时考虑子模型间相互作用的情况，提出一种新的Markov 转移概率实时修正的方式。仿真结果，本文算法可以进一步提高模型的切换速度，提高跟踪精度和稳定性，具有更好的机动目标跟踪性能。

2 系统模型和跟踪方法

2.1 目标运动模型

假定在x-y二维监控区域有一运动目标，它根据匀速（Constant Velocity，CV）模型或匀加速（Constant Acceleration，CA）模型移动，则可对目标进行如下的建模：

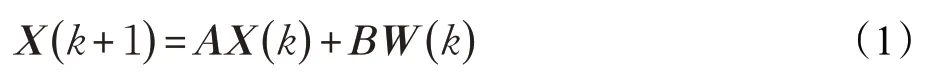
当目标根据CV模型运动时，理想的加速度应为零，目标运动过程中会受到随机的扰动，其加速度不可能为零，即。

因此可将系统表示为：

式中，T为采样间隔。

整理成矩阵形式，可得CV 模型的状态转移方程如下：

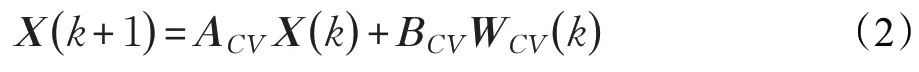
ACV和BCV分别如下：

同理，当目标根据CA模型运动时，目标的加速度保持不变，即加速度的导数应为零，由于目标运动过程中会受到随机的扰动，加速度的导数不可能为零，即表示分别表示k时刻目标在x、y方向的加速度的导数，则作对应的积分可求得k时刻目标在x、y方向的加速度，速度和位置。

因此可将系统表示为：

整理成矩阵形式，可得其状态转移方程如下：

ACA和BCA分别如下：

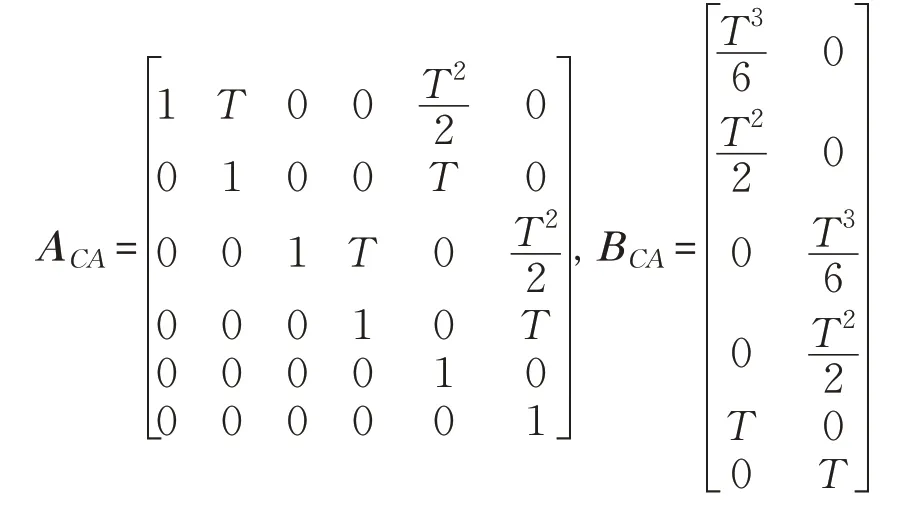
2.2 观测模型

假定WSN 由Ns个随机分布在监控区域内的锚节点组成，其位置记为si,i∈{1 ,2,…,Ns} 。并且所有的锚节点以相同的初始功率在网络中周期性地广播信号。运动目标携带一个信号接收器，在运动过程中接收由Ns个锚节点发送的信号。在监控区域中配备一个处理器，并假设其具有足够的通信范围，且能与网络中运动目标携带的传感器相互通信。

为了对节点进行定位，首先用无线电指纹对网络进行建模。为此，在监控区域中选取Np个参考点，其位置记为pl,l∈{1 ,2,…,Np} 。在每个参考点放置可以接收到锚节点信号的传感器，并在这些位置测量它们的RSSI值，记为ρl=[ρs1,pl,ρs2,pl,…,ρsNs,pl]T，由此可以得到无线电指纹库，其存储形式为[pl:ρl] ，表示在位置pl测得的RSSI向量为ρl。在k时刻，目标节点接收到的由锚节点发射信号的RSSI值，记为ρ(k)=[ρ1(k),ρ2(k),…,ρNs(k)]T。根据所收集到的位置指纹信息，本文利用支持向量回归（Support Vector Regression，SVR）算法[18]构建一个输入为ρ(k)，输出为传感器节点位置的函数ψ(⋅):RNs↦R2。即

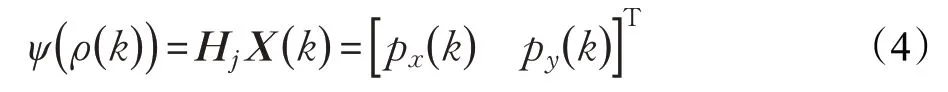
因此传感器的观测模型如式（5）所示：

式中，z(k)为传感器量测向量；n(k)为量测噪声，假设n(k)～N( 0,R)；量测矩阵Hj如下：

2.3 IMM算法

IMM 算法采用多个滤波器并行处理，在滤波输出阶段通过有效的加权融合得到最终的状态估计。在模型集的选择中，本文采用一个CV模型和两个加速度噪声不同的CA 模型，即m=3。假定每个模型对应的模型概率记为μj(k)，Markov 概率转移矩阵表示为P={pij,i,j=1,2,…,m} ，则IMM算法的基本过程可表示如下：

步骤1交互输入。由上一时刻目标的状态估计和每个模型对应的概率μi(k-1) ，可以得到混合估计Xoj(k-1|k-1) 和协方差Poj(k-1|k-1) 。

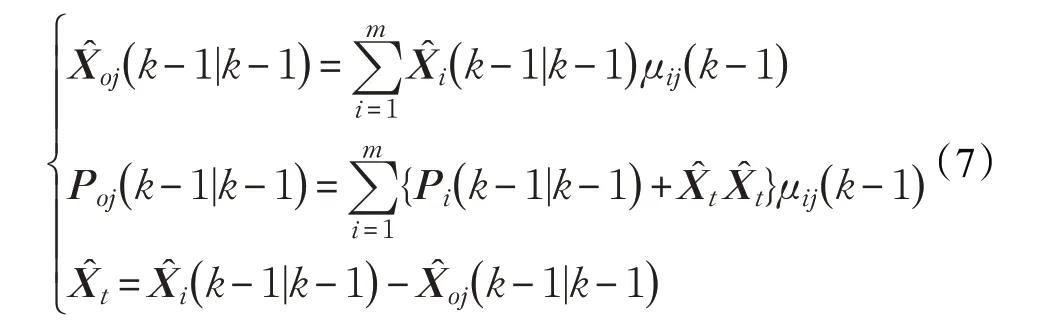
式中：

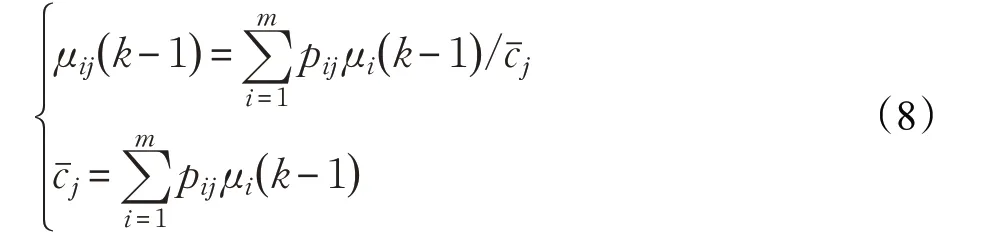
步骤2扩展卡尔曼滤波。将k-1)和z(k)作为扩展卡尔曼滤波的输入，可得到对应的状态估计值。

预测

更新

式中，卡尔曼增益Kj为：

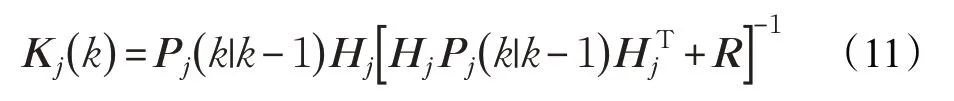
步骤3模型概率更新。利用模型j的似然函数来更新模型概率μj(k)。

模型j的似然函数为：

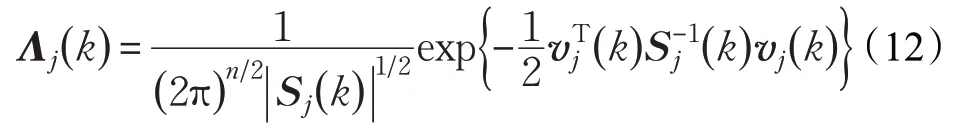
式中，vj(k)和Sj(k)分别表示为：

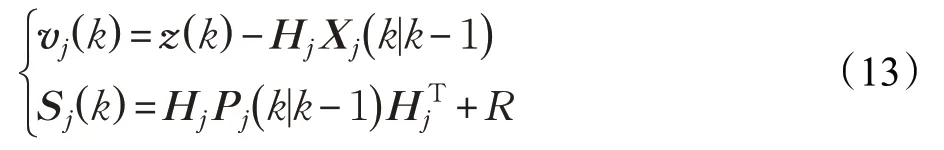
模型j的后验概率为：

步骤4输出交互

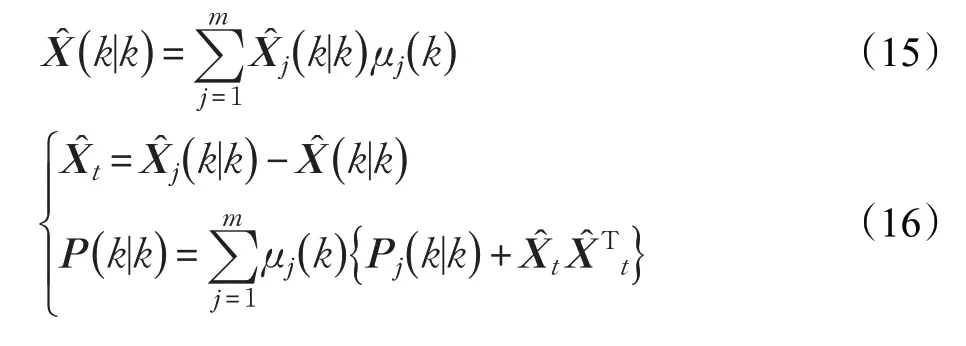
3 FNN-AIMM算法

由式（15）可知，IMM 算法最终输出的状态估计的准确性取决于IMM算法子模型对应的概率。

从式（14）可知，Markov 概率转移矩阵P和观测噪声协方差矩阵R是影响模型概率准确更新的重要参数。然而，在算法迭代过程中，通常假设它们是先验已知的。因此，为了提高跟踪精度，本文将从如下两个方面对传统的IMM 算法进行改进。首先根据IMM 算法输出系统残差协方差矩阵的理论值与统计值之间的差异，引入FNN，在模型输出阶段自适应地调整观测噪声协方差矩阵。其次，考虑IMM 算法子模型间相互作用的情况，提出一种新的Markov 概率转移矩阵实时修正的方式。

3.1 利用FNN调整观测噪声协方差矩阵

由公式（15）可得，IMM算法输出的残差为：

残差协方差矩阵的理论值为：

式中：

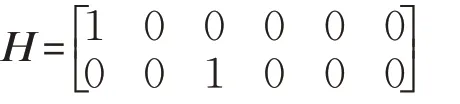
残差协方差矩阵的统计值为：

式中，N为移动估计窗口的大小，k0=k-N+1。

T(k)和E(k)之间的差值为：

从式（18）～（20）可知，当测量噪声协方差矩阵R主对角线元素增加或者较小时，矩阵Di主对角线的元素也作相应的变化。因此，可以利用矩阵Di的值来对R进行调整，从而减小T(k)和E(k)之间的差异。本文假设传感器对于不同坐标轴的测量噪声是不相关的，因此R2是一个主对角线元素为零，其余元素不为零的矩阵，故只需调整主对角线的元素即可。

输入输出语言变量定义如下：

Di：负 (N)，零(Z)，正(P)

ΔRi：减小 (D)，不变(M)，增加(I)

由此可定义如下的模糊系统的规则，使得理论协方差与统计残差协方差之间的差异最小：

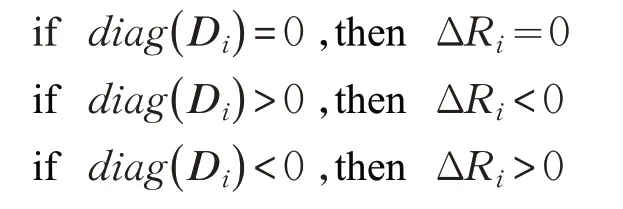
Di，ΔR的隶属度函数如图1所示。

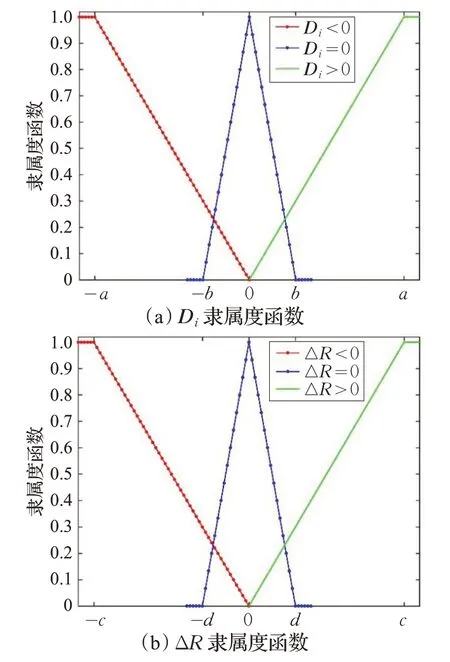
图1 隶属度函数

本文采用T-S 模糊神经网络[19]来构建Di与ΔR之间的模糊推理机，网络每个神经元的输出如图2所示。

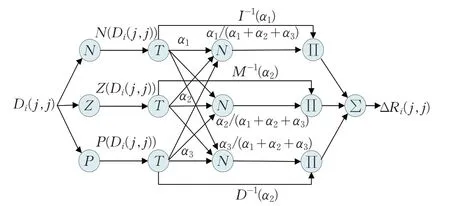
图2 模糊神经网络

根据最大-最小原则进行解模糊，可得到网络的最终输出为：

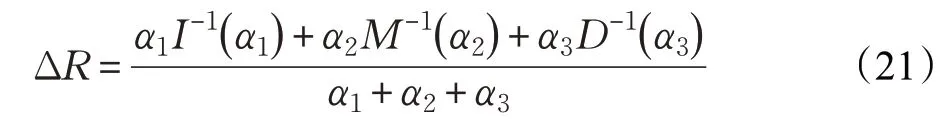
式中，I-1(α1)、M-1(α2)和D-1(α3)表示其对应的反函数。

因此，在k时刻测量噪声协方差矩阵R可根据式（22）自适应调整：

式中，Rk(j,j)为k时刻矩阵R第j行j列的元素。

给定数据集{(D1,ΔR1),(D2,ΔR2),…,(Dk,ΔRk)}，定义数据(Dj,ΔRj)的训练误差为：

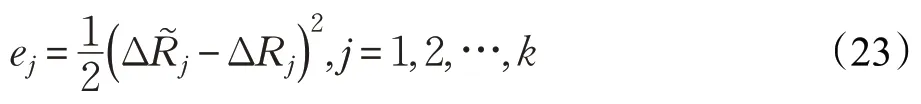
式中，λ ＞0 为学习速率，n为迭代次数。当训练误差小于一定值或者达到最大迭代次数时，停止迭代，即可得到FNN隶属度函数的参数a，b，c，d。

3.2 Markov转移概率实时修正

传统的IMM 算法假定系统输入交互过程是一个Markov过程[21]，即

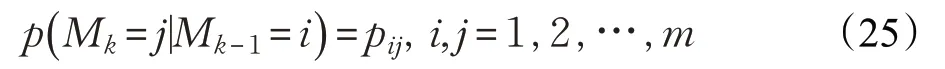
式中，Mk=j为k时刻系统匹配的模型为j，pij表示模型i转移至模型j的概率。

传统的IMM 算法采用固定Markov 转移概率矩阵不能准确地反映目标实际运动模式之间的切换情况，进而造成较大的跟踪误差[22]。因此，在滤波过程中应利用后验信息对Markov 转移概率矩阵进行实时修正，使之符合实际情况。

模型概率μj(k)表示k时刻模型j与目标真实运动模式的匹配度，则相邻时刻模型概率的变化可以反映模型j与目标运动模式匹配度的变化情况。文献[16]利用相邻时刻模型概率的差值对Markov转移概率矩阵进行实时修正。但这种方法只考虑一个模型概率的变化情况，没有考虑模型间交互的情况，增大匹配模型的作用有限。

为进一步增大匹配模型的作用，抑制非匹配模型的影响，本文考虑模型之间相互作用的情况，利用相邻时刻模型概率之比对Markov 转移概率进行实时修正，修正如下：

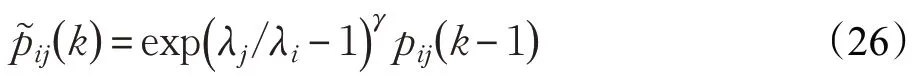
式中，λj=μj(k)μj(k-1) ，γ为比例系数。

从式（26）可以看出：

（1）若k时刻模型i和模型j的概率同时增大 (λi ＞1,λj ＞1)或减小(λi ＜1,λj ＜1)时，若λj/λi ＞1，则exp(λj/λi-1)γ ＞1，说明与模型i相比，模型j与目标真实运动模式更匹配，经过式（26）修正后由模型i切换至模型j的概率pij也随之增大，因而在下一时刻的输入交互过程中，模型j在交互输出过程得到的模型概率μj(k+1) 也随之增大；若λj λi ＜1 ，则 exp(λj/λi-1)γ＜1 说明模型i与目标真实运动模式更匹配，经过修正后由模型i切换至模型j的概率pij也随之较小，进而在下一时刻的交互输入过程中，模型j在交互输出过程得到的模型概率μj(k+1)也随之减小。

（2）当模型j的概率增大而模型i的概率减小时，即λj ＞1、λi ＜1 ，此时 exp(λjλi-1 )γ会进一步大于 1，说明模型j与目标的运动模型匹配程度更高，则经过式（26）修正后由模型i切换至模型j的概率pij将进一步增大，进而进一步增大了匹配模型的作用。

（3）当模型j的概率减小而模型i的概率增大时，即λj ＜1、λi ＞1 ，exp(λj λi-1 )γ会进一步小于1，说明模型i与目标的运动模型匹配程度更高，则经过式（26）修正后由模型i切换至模型j的概率pij将进一步减小，对不匹配模型的抑制会更加明显。

考虑到k时刻某一模型向其他模型切换的概率为1，因此需对式（26）进行归一化，即

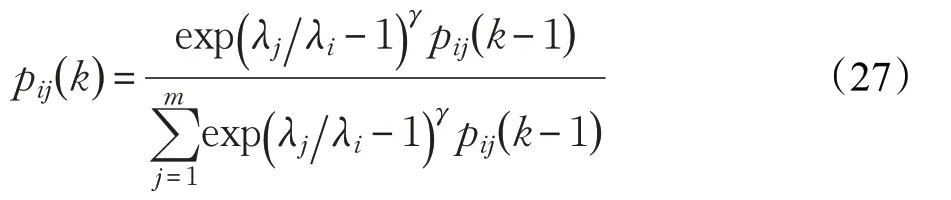
由于Markov概率转移矩阵须满足主对角线元素占优的条件。因此，在算法迭代过程中，应判断经式（27）调整后的Markov概率转移矩阵是否满足：

如果满足，则更新转移概率，反之，则不更新。

FNN-AIMM算法流程图如图3所示。

图3 FNN-AIMM算法流程图

4 仿真与结果分析

4.1 利用模拟数据对提出的方法进行分析

假定目标在100 m×100 m的监控区域内移动，其中监控区域由16个锚节点组成，选取100个参考点构建无线电指纹库。RSSI由Okumura-Hata模型[23]产生：

式中，ρsi,Pl表示的是在pl处接收到由锚节点si传来的功率；ρ0为传感器的初始发射功率，假设为100 dBm；np为路径损耗系数，假设为4；εi,l为影响RSSI测量的噪声，假设均值0方差为1 dBm的高斯白噪声。

假定目标的初始的状态和协方差矩阵分别为X( 0)=[20 1 10 0 0 0]T和P( 0)=10-2I，其中I为单位矩阵。模型集为CV模型和两个加速度噪声不同的CA模型。对于CA 模型，其过程噪声协方差矩阵为QCV=diag(0.01,0.01) ；对于CA 模型，其噪声协方差矩阵分别为QCA1=diag(0.1,0.1) ，QCA2=diag( 1,1) 。仿真采样间隔T=1 s，仿真时间t=260 s。目标实际运动模式如表1和表2所示。

表1 CV运动 m·s-1

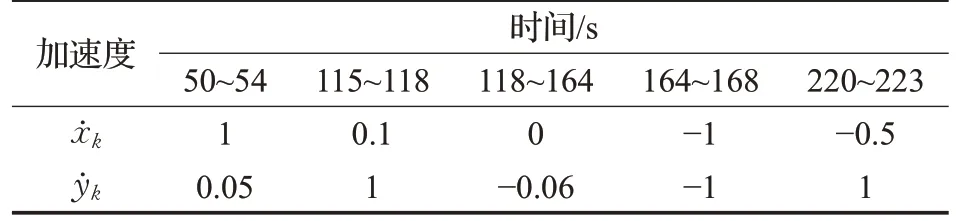
表2 CA运动m·s-2

给定训练数据集{(D1,ΔR1),(D2,ΔR2),…,(Dk,ΔRk)}，其中k=1 000。FNN 初始隶属度函数Di、ΔR的参数分别为a=5,b=1.5,c=0.5,d=0.1。梯度下降算法中的学习速率λ=0.1，迭代次数n=2 000，训练后得到的参数分别为a=4.192;b=1.3;c=0.411;d=0.095。

在IMM 算法中，控制模型切换速度的比例系数γ=0.8，Markov概率转移矩阵主对角线的阈值Th=0.5，初始Markov概率转移矩阵及各模型的初始概率为：

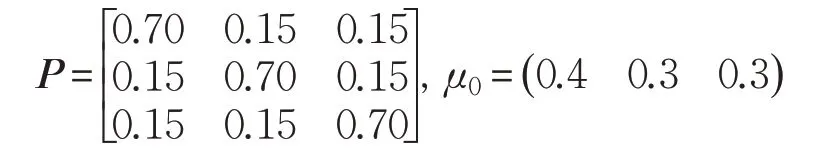
图4 表示的是使用四种方法，Monte Carlo 仿真500 次的均方根误差曲线。这四种方法分别是标准的IMM算法、本文提出的算法、文献[15]和文献[16]提出的方法。

表3为不同算法的平均均方根误差，峰值误差的对比结果。

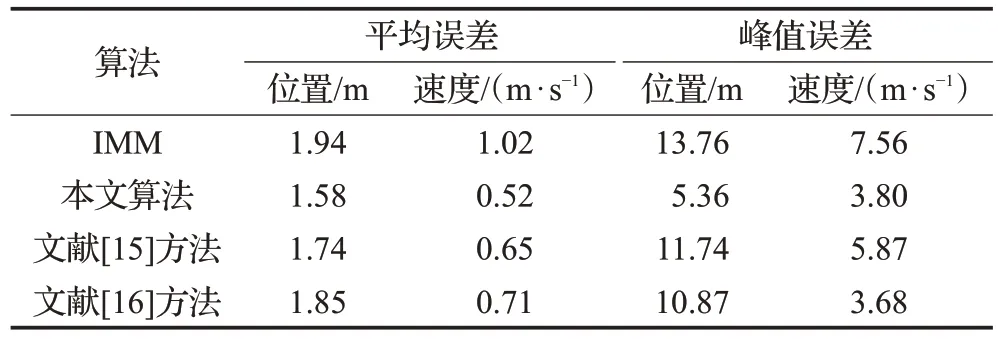
表3 RMSE比较

从图4 以及表3 可以看出，无论是位置均方根误差还是速度均方根，在绝大多数数情况下，本文方法的误差都是最小的，跟踪精度较标准的IMM 算法有大幅度提升，且优于文献[15]和文献[16]提出的方法。在峰值误差方面，优势同样明显，位置峰值误差远小于其他方法，速度峰值误差略大于文献[16]的方法。说明本文的方法能够对目标进行全面自适应的跟踪，具有良好的适应性。

图5 为在某次实验中各算法的模型概率变化曲线。从中可以进一步看出，与其他三种方法相比，本文给出的方法可以较大地提高子模型之间的切换速度，并且切换后能够快速收敛。模型概率的变化较为准确地反映了目标实际运动模式的变化情况。尤其是当目标在短时间内实施机动时，如t=50～54 s、115～117 s、220～222 s，本文给出的方法可以迅速对模型概率进行调整。这是因为本文除了利用子模型相邻时刻的模型概率之比对Markov 转移概率进行实时修正外，还对观测噪声协方差矩阵进行自适应调整，进一步增大了匹配模型的作用，削弱不匹配模型的影响。

图4 均方根误差对比

图5 模型概率变化曲线

4.2 利用真实数据对提出的方法进行分析

为了进一步评估所提出的方法的性能，选用如图6所示的会议室作为实验环境获取RSSI。在7.8 m×6.6 m的会议室布置4个静止的传感器节点，和一个移动的目标节点，传感器的型号为CC2530。目标节点约每0.1 s向外广播信息。在离线阶段，选取24 个参考点构建无线电指纹库。

图6 实验环境拓扑

目标节点的初始状态为X( 0)=[0.6 0.3 0 0 0 0]T，CV模型过程噪声Q1=diag(0.3,0.3 )，两个CA模型的过程噪声分别为Q2=diag(0.5,0.3 )、Q3=diag(0.1,0.1) ，其他参数的设置同4.1节。

图7和图8分别表示所给出的方法与其他方法的跟踪结果和对应的位置偏差。并对平均跟踪误差进行统计，结果如表4所示。

图7 跟踪结果

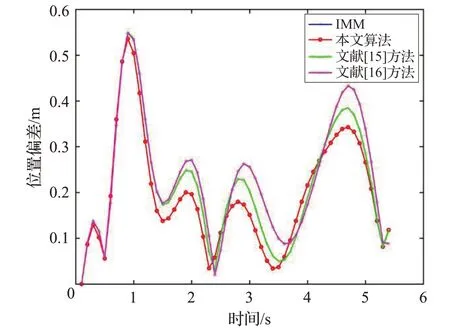
图8 一次运行位置偏差

表4 平均跟踪误差

从图7、8 以及表4 中可以看出，本文所提出的方法在跟踪精度上优于其他三种方法。尤其是当目标运动状态发生突变时，与其他仅对Markov 转移概率矩阵实时修正的方法相比，本文所给出的方法能够进一步增大匹配模型的作用，减小非匹配模型的影响，对机动目标具有更好跟踪效果。

5 结束语

本文提出了一种具有模型概率实时修正的IMM机动目标跟踪算法。该算法首先在监控区域构建无线电指纹库，然后利用SVR 算法构造观测方程。为了提高IMM 算法子模型之间的切换速度和合理性，引入FNN对观测噪声协方差矩阵进行估计。同时，利用IMM 子模型中两个连续时间点的概率比，对Markov 概率转移矩阵进行实时修正。通过模拟数据和实际传感器采集的数据进行仿真分析，结果表明，所提出的方法在跟踪精度及实时性优于IMM算法、文献[15]和文献[16]的方法，对机动目标具有较好的跟踪效果。