SparkSql上自适应数据集的高效频繁集挖掘算法

王永贵，郭昕彤

辽宁工程技术大学 软件学院，辽宁 葫芦岛 125105

1 引言

在如今这个数据呈指数级增长的互联网时代，每天的这些海量数据之中不乏有很多具有重要价值的信息，而关联规则挖掘则可以发现大量数据中项集间的关联[1]。分布式和并行计算正是为了解决在实际应用中大数据量的存储和计算效率问题[2]。Spark 则为最常用的分布式计算框架。Spark是在借鉴了MapReduce的基础之上发展而来，相比较于MapReduce它继承了分布式计算的优点[3]并对过大的I/O开销、低效率，以适用于多迭代算法不够灵活等问题都做出了重大改进。

Qiu等人[4]提出YAFIM算法，这是首次在Spark上实现了Apriori 算法的并行化。它引进了Spark 的弹性分布式数据集RDD 的抽象且支持DAG 图的分布式并行计算的编程框架，减少了迭代过程中数据的落地，这很好地解决了MapReduce 框架存在的问题[5]。该算法的实验结果也说明了在Spark上实现传统算法的效率相比基于Hadoop上的有很大改善。但算法在执行过程时自连接存在难题，得到的频繁集会多次扫描已有的数据库，当候选集数目庞大时，会很大地降低算法的效率。Rathee 等人[6]在YAFIM 算法的基础上消除了候选集的生成过程并且引入了布隆过滤器，利用布隆过滤器相比较于哈希树的空间和时间的优势代替了哈希树，与YAFIM 算法相比具有更高的扩展性以及加速比，但是算法生成过多无用项集，同时算法泛化性较差。Luo等人[7]基于Spark提出稀疏布尔矩阵分布式频繁挖掘算法FISM，算法通过事务与项目构成的矩阵减少了扫描数据库的次数，算法性能有了提高但还是有大量重复性操作。而后谢志明等人[8]提出了Apriori_MMR算法，该算法也是引入了布尔矩阵但结合数据分片进行了并行化实现，通过矩阵化使事务数据库得到进一步的压缩，在大数据集上挖掘时其效率及性能上均有较大提升。但其中布尔矩阵无法将数据存储在某小节点上垂直划分，所以还存在着一定的局限性。Krishan 等人[9]提出了一种新的混合频繁项集挖掘算法，该算法利用数据集的垂直布局来解决每次迭代中数据集的扫描问题，垂直数据集携带信息以查找每个项目集的支持度使得计算起来变得简单，但同时也占用过多的内存。Karim 等人[10]提出了一种利用Spark 平台挖掘最大频繁模式的有效方法，利用一个基于素数数据转换技术。Chon等人[11]充分利用CPU 的计算能力执行大量数据，进而提升算法候选集的生成以及支持度计数的速度。

虽然上述从不同角度上提出了改进方法，一定程度上提高了算法性能，但存在挖掘模式单一、计算支持度的方法复杂、计算许多无用数据、数据量大时受限于RDD的存储和计算效果。

2 相关知识

2.1 SparkSql

Spark SQL是Apache Spark中的一个新模块，提供了关系处理的丰富集成[12]。它用于处理结构化数据的模块，包括一个基于成本的优化器、列存储和代码生成，以加快查询速度[13]，与此同时使用Spark 引擎扩展到数千个节点和多小时查询，提供了完整的中间查询容错。它使用声明性DataFrame API扩展Spark以允许关系加工，提供诸如自动优化等优点，让用户编写混合了关系和复杂分析的管道[14]。

RDD是分布式的Java对象的集合，DataFrame是分布式的Row对象的集合。DataFrame除了提供了比RDD更丰富的算子以外，更重要的特点是提升执行效率、减少数据读取以及执行计划的优化，比如filter下推、裁剪等。因为它规定了具体的结构对数据加以约束。由于DataFrame具有定义好的结构，Spark可以在作业运行时应用许多性能增强的方法。例如，定制化内存管理：数据以二进制的方式存在于非堆内存，节省了大量空间之外，还摆脱了GC的限制；优化的执行计划：查询计划通过Spark catalyst optimiser 进行优化。Spark 对于DataFrame在执行时间和内存使用上相对于RDD有极大的优化[15]，Catalyst优化引擎使执行时间减少75%、Project Tungsten Off-heap内存管理使内存使用量减少75%。

本文算法基于SparkSql的分布式数据结构DataFrame进行编程，解决了RDD内存资源和计算速度受限问题，使得本文算法在标准数据集上得到更高效的结果。数据集存储在RDD和DataFrame上的区别如图1所示。

图1 数据集基于RDD和DataFrame存储的区别

2.2 倒排索引

倒排索引[16]源于实际应用中需要根据属性的值来查找记录。这种索引表中的每一项都包括一个属性值和具有该属性值的各记录的地址。由于不是由记录来确定属性值，而是由属性值来确定记录的位置，因而称为倒排索引。本文引入倒排索引的思想来优化支持度的计算，取代通过判断数据集中包含项集的事务个数来计算支持度的方法，避免每次支持度都要访问一次数据集，产生巨大的I/O 开销[17]。本文在计算支持度时的具体优化如下。

（1）将数据集加载到SparkSql，以DataFrame结构存储，其事务列为包含对应项集列中项集所在的事务集合，集合的长度即所求支持度。

（2）候选集的k个项目对应事务列的集合交集，即k个项目共同存在的事务集合，也就是包含候选集的事务集合。计算候选集k项集的支持度时，通过执行Spark-Sql语句对DataFrame中对应k个项目的事务列求交集，得到集合的长度，即候选集的支持度。

本文算法挖掘所有频繁集只需要读取一次数据集，同时每次计算候选集支持度，只需计算候选集的k个项目而不必计算整个数据集；计算支持度的过程中，利用SparkSql语句求交集的方法，较基于RDD编程计算支持度的方式提升执行效率、减少数据读取以及执行计划的优化。支持度计算过程如图2所示。

图2 支持度计算示例图

2.3 布隆过滤器

布隆过滤器是一种概率型数据结构，特点是高效地插入和查询，可以用来判断某个元素或集合是否存在，它是用多个哈希函数，将一条数据映射到位图结构。例如，判断一个项目是否在数据集中，布隆过滤器将数据集中每个项目都通过k个不同的Hash函数随机散列到数组的k个位置上，并将这些位置置为1。现要判断项目w是否在数据集中，通过Hash函数将事务w映射成位阵列中的点，判断这些点是否都为1，可以得到元素是否存在于数据集。示例如图3所示。

图3 布隆过滤器示例图

布隆过滤器随着k的个数增加，可以提升布隆过滤器的存储效果，但是也会增大内存访问次数和计算复杂度，降低算法效率。本文算法通过添加存储集合元素的辅助信息，即唯一ID，改进后访问一次相当于布隆过滤器的两次访问，同时辅助信息中存储了项目对应的事务位置，可以有效地减少频繁集挖掘过程中查找项目属于某个事务所浪费的计算资源，并减少访问内存的次数，提升运行速度。

构建阶段分三步进行。（1）设K2+1个独立的Hash函数，H(x)={h0(x),h1(x),…,hk2(x)}使其具有均匀分布的输出数据的能力，构造一个m位大小的数组B，其中每个比特被初始化成0；（2）存储集合S的元素信息，计K2+1个哈希值与此同时还需要计算集合S的元素e的偏移值为每个元素的辅助信息O(e)；（3）将K2+1 位B[h1(e)%m],B[h2(e)%m],…,B[hk2(e)%m]置为 1，同时将K2+1 位B[h1(e)%m+O(e)],B[h2(e)%m+O(e)],…,B[hk2(e)%m+O(e)]置为1。设B[hi(e)%m]为第j个 bit（一个字节的位j，1 ≤j≤8），读取它之前需要读j-1 位。为了一次访问内存读取B[hi(e)%m]、B[hi(e)%m+O(e)]，需要一次内存读取访问j-1+wˉ位，所以j-1+wˉ＜w当j取最大值8时，wˉ＜w-7，则为保证在一次内存读取中获得B[hi(e)%m]、B[h1(e)%m+O(e)]需要wˉ＜w-7（64 位系统=64）。O(e)≠0，若O(e)=0则B[hi(e)%m]、B[h1(e)%m+O(e)]两位在数据的相同位置。构建阶段最大哈希函数的数量为K2+1。查询是项目e是否存在于集合B：用一次内存读取元素位置和唯一ID的偏移位置，如果两位同时为1，读取下两位，如此遍历。当所有位都为1，得出元素存在于集合中。判断一个项目是否存在的最大内存访问次数比布隆过滤器减少了一半，从而减少了计算时间。改进后的布隆过滤器的数据结构如图4所示。

图4 改进的布隆过滤器的数据结构

3 本文算法

本文提出一种基于SparkSql 的分布式编程的算法。首先，利用SparkSql 存储数据集和计算支持度、改进后的布隆过滤器存储迭代过程生成的项目集；其次，通过精简步得到频繁项目、候选集、事务集；最后，提出两种迭代的方法和选择条件，自适应数据集选择最优方式进行频繁集挖掘的算法。本文算法分两个阶段进行。第一阶段从数据集中挖掘出所有的频繁一项集。第二阶段从数据集中迭代挖掘出所有频繁项集。

3.1 精简步

本文基于先验定理在每次迭代过程进行精简事务集、项目和候选集。基于SparkSql 的DataFrame 数据结构的高效性对项目、事务进行精简；针对改进后布隆过滤器上精简后的候选集支持度的计算进行简化。算法通过精简条件的前三步删除不能生成频繁集的事务、项目、候选集，减少频繁集挖掘过程需要计算的数量同时第四步优化支持度的计算方法，进而达到提升频繁集挖掘效率并节省计算资源的目的。具体精简过程如下。

（1）频繁k集必须由k(k-1)/2 个频繁子集生成，删除频繁子集个数不等于k(k-1)/2 的候选集。

（2）频繁k项集必须有k个项目组成，删除频繁项目数小于k的事务。

（3）频繁k项集必须由频繁项目组成，删除不频繁的项目。

（4）算法基于项目-事务-计数的DataFrame，通过对所求项目集中每个项目对应的事务列求交集，得到支持度。

例如图5 是数据集加载到SparkSql 的Dataframe 结构，最小支持度为50%挖掘频繁集。第一次迭代，除了a、b都为频繁一项集、第二次迭代的事务至少有两个项目，必须都是频繁项目，所以删除T1、T6、a、b，最后对候选二项集对应T列求交集得到频繁二项集cg、dg、fg。第三次迭代，频繁三项集必须有3 个频繁子集，候选集cdg、cfg、dfg，都只有2个频繁子集，所以没有频繁三项集，不必计算，挖掘过程结束。

图5 精简示例图

3.2 迭代条件

第k次迭代，事务个数t，每个事务中的平均项目个数n，频繁k-1 项集数g，频繁项目个数i，频繁候选集个数c，布隆过滤器中存储和搜索一个元素花费的时间为1。由先验定理可以得出公式（1）：

第一种方法迭代时的三个步骤：第一步频繁k-1项集存储到布隆过滤器中的时间Ts。第二步生成和精简候选集的时间Tn。第三步生成键值对的时间Tj。

第k次迭代花费的时间为Ta：

存储频繁k-1 项集到布隆过滤器中的时间为：

生成频繁候选集和精简候选集的时间为：

生成精简候选集的键值对时间为：

第k次迭代的时间为：

第二种方法迭代时所用时间的三个步骤：第一步生成频繁事务和项目的时间Tg。第二步存储频繁k-1项集的项目在布隆过滤器中的时间Tq。第三步生成键值对的时间Tj。方法2进行第k次迭代：

生成频繁事务和项目的时间：

频繁k-1 项集中的频繁项目存储在布隆过滤器中的时间：

生成键值对的时间：

第k次迭代的时间：

精简的候选集c一定小于等于候选集个数 |Ck|，得到如下条件。如果满足Tb ＞Ta就用方法1，反之用方法2。

3.3 算法实现

第一阶段从数据集挖掘出所有频繁一项集。首先，定义一个模式字符串“Item Tid Count”，根据模式字符串，生成模式（Filed）。其次，用Schema 描述模式信息，模式中包含Item、Tid、Count三个字段。最后，数据集加载到DataFrame，注册为临时表，通过sql 语句生成频繁一项集。频繁一项集的挖掘过程如图6 所示。频繁一项集的挖掘应用示例如图7所示。

图6 频繁一项集的挖掘过程

图7 频繁一项集挖掘的应用示例

第二阶段获取频繁k+1 项集。迭代地使用k项频繁集来生成k+1 项频繁集，直到没有频繁集生成或达到终止条件。基于当前迭代数据集和频繁k项集的特征，使用一个动态方法选择生成候选集的方法即方法1或者不生成候选集的方法即方法2来完成第k次迭代，如果该次迭代满足条件用方法2进行迭代，否则用方法1算法进行挖掘频繁k项集。

第k次迭代，如果不满足条件，使用方法2 完成本次迭代。首先，将频繁集中的频繁k-1 项集中的项目存储在布隆过滤器；其次，应用intersection 算子于DataFrame 进行修剪，删除不存在于布隆过滤器中的频繁项目；再次，应用map 算子，删除项目事务DataFrame中项目数小于k的事务，应用map算子于布隆过滤器中的频繁项目，映射生成可能出现的k项集；最后，通过sql 语句得到k项集中每个项目对应的事务集合的交集，从而计算支持度，进而得到频繁集。

如果满足条件，使用方法1 进行本次迭代。首先，将频繁集中的频繁k-1 项集中的项目集合存储在布隆过滤器。其次，连接前k-2 项相同的频繁k-1 项集，生成候选k项集。再次，删除频繁k-1 项子集不等于k(k-1)/2 的候选集。最后，通过sql 语句得到k项集中每个项目对应的事务集合的交集，从而计算支持度，进而得到频繁集。频繁k项集的挖掘流程如图8 所示。应用示例如图9所示。

图8 频繁k 项集挖掘过程

图9 频繁二项集生成的应用示例图

4 实验

4.1 实验数据

实验数据是UCI 中六个用于验证关联规则算法性能，并且特点不同的数据集，具体如表1所示。

4.2 实验环境

实验的软件环境为64 位Ubantu 14.04 Linux 操作系统、JDK-1.8 Hadoop-2.7.1 Scala-2.12.1 Spark-1.6.1Python-3.6.3 Anaconda-2.0；硬件环境为Intel corei7-6500U 处理器，4 个 3.10 GHz 处理器核、8 GB RAM 和500 GB HD。采用20 台计算机搭建Spark 集群运行环境，集群共20个节点，把其中两台计算机设为master节点，其他18台机器设为slave节点。

表1 实验数据集

4.3 实验性能

实验采用增加节点的个数M和数据集的复制倍数N为变量，用SpeedUp、SizeUp、ScaleUp 等评估指标验证算法的性能。选用Retail 数据集、Musroom 数据集、Kosarak 数据集、BMSWebView2 数据集四个不同数据集，在最小支持度为0.1%的条件下对算法进行验证。

随着集群节点数M增加，加速比变化情况如图10所示。算法在不同数据集中随节点数的增加，加速比总会达到最优值，并且加速比最终都呈稳定趋势，进而证明该算法可以应用于更大的集群规模。

图10 随着节点增加，算法SpeedUp的变化

在节点数为6的条件下，随着数据集复制倍数的增加，观察算法应用在不同数据集的SizeUp 的变化情况如图11 所示。随着不同数据集的倍数增长，算法的SizeUp呈缓慢的增长趋势，说明本文算法具有处理更大数据集的能力。

随着节点数M和数据集复制倍数N的同时同倍数增加，观察算法应用在不同数据集的SizeUp 的变化情况如图12 所示。随着数据集复制倍数和集群节点数同向增长时，观察算法对不同数据集的ScaleUp 一直在0.9 附近稳定波动，进而证明该算法当应用到大规模计算时，具有较好的高效性和泛化性。综上所述，本文算法可以应用到更大规模数据和集群条件下挖掘频繁集。

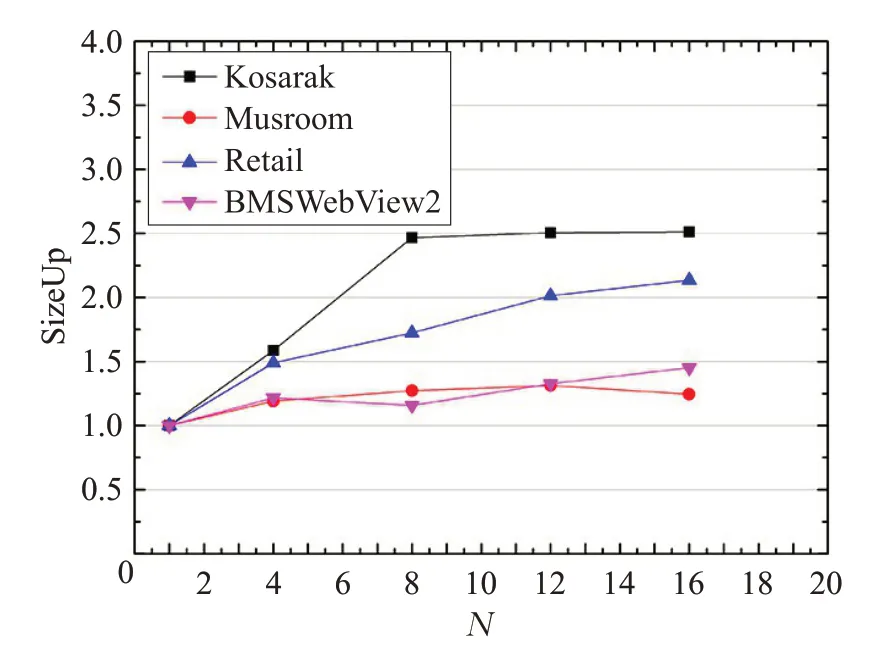
图11 随着数据量增大，算法SizeUp的变化

图12 随着节点和数据同时增大，算法ScaleUp的变化

4.4 对比实验

将本文提出的两种频繁集挖掘方法和最终算法基于Musroom 数据集和Kosarak 数据集，分别在最小支持度为0.3、0.1%的条件下方法1、方法2 和本文算法的比较，如图13 和图14 所示。实验结果表明本文算法每次迭代会选择最优的迭代方法，从而提升每一次迭代的计算效率，进而提升算法的高效性。与此同时，本文算法在不同数据集和支持度时总是选择最优的迭代方法，有着很好的泛化性。

本文选用基于Spark框架的R-Apriori算法和YAFIM算法进行对比实验。将上述两种算法和本文算法基于T10I4D100K 数据集、BMSWebView2 数据集和 Retail 数据集，分别在支持度为0.1%、0.15%、0.5%的条件下进行对比，如图15和图16、图17所示。实验结果表明本文算法在不同数据集和支持度的条件下，挖掘频繁集的每次迭代过程相较于两种对比算法都表现出更高效的计算效率，进而证明本文算法有更好的高效性和泛化性。

将本文算法和对比算法基于Kosarak 数据集和BMSWebView2 数据集上，分别在支持度为0.1%、1%、10%的条件下进行对比，结果如图18 和图19 所示。实验结果表明本文算法不同数据集和支持度的条件下，在挖掘所有频繁集的总运行时间上优于两种对比算法，进而证明本文算法在挖掘大数据中所有的频繁集上，有更好的高效性和泛化性。

本文基于不同数据集，不同支持度进行对比实验，通过上述实验可以得到以下结论。在总挖掘效率上优于两种对比算法；在挖掘频繁集的每一次迭代根据数据集的特点总是选择最优的方法；在挖掘频繁集的每一次迭代都较好于两种对比算法；综上所述，本文算法有着较好的高效性和泛化性。

图13 基于Musroom数据集、min_sup=0.3的条件，算法对比

图14 基于Kosarak数据集、min_sup=0.1%的条件，算法对比

图15 基于T10I4D100K数据集、min_sup=0.1%的条件，算法对比

图16 基于BMSWebView2数据集、min_sup=0.15%的条件，算法对比

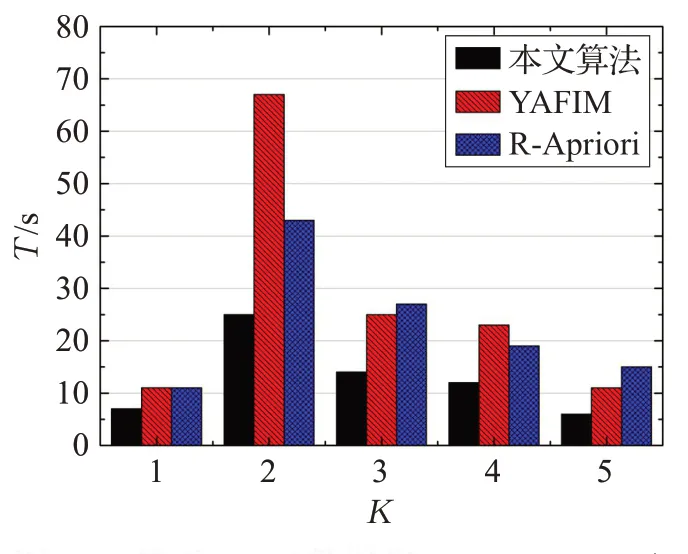
图17 基于Retail数据集、min_sup=0.5%的条件，算法对比

图18 基于Kosarak数据集不同支持度下算法对比

图19 基于BMSWebView2数据集不同支持度下算法对比

5 结束语

本文算法围绕如何提升算法计算效率进行改进。首先，基于SparkSql分布式编程，减少算法对单台服务器造成的压力，将数据集加载到DataFrame，解决了RDD内存资源和计算速度受限问题；其次，充分利用改进后的布隆过滤器存储过程数据的时间和空间优势来满足挖掘过程中的存储、查询项集的需求；再次，基于先验定理对事务、项目和项集进行精简，同时通过对项集中项目对应事务集合求交集的方式计算项集支持度，进而提升支持度计算效率和避免大量不必要的数据存储；最后，提出了两种迭代算法和选择条件，增强本文算法对各种数据集的泛化性。本文进行了多组性能实验和对比实验，实验结果表明，算法有效提升挖掘所有频繁集的效率，同时较好地提升每次迭代效率；每次迭代总是根据数据集特点选择最优的迭代方式；通过多个并行算法评估指标验证本文算法有着较好的泛化性和高效性，可以应用到更大规模的数据集和集群。