一种计算航船对近海海洋环境噪声贡献的算法
戎泽存,胡长青,赵 梅
(1.中国科学院声学研究所东海研究站,上海201815;2.中国科学院大学,北京100049)
0 引 言
海洋环境噪声作为背景场,在很长一段时间里是被当作干扰项来看待,而事实上海洋环境噪声中包含着丰富的信息,因此它具有重要的研究价值。海洋环境噪声的组成比较复杂,学界普遍认为航船噪声和风成噪声是两大主要组成部分,前者主要影响的是中低频段噪声(10~500 Hz),后者主要影响的是较高频段噪声(500~25 000 Hz)。除了以上两大主要组成外,在低频段(1~100 Hz),潮、涌、浪、大尺度湍流以及远处的地震、风暴均对海洋环境噪声产生贡献[1]。
作为一种随机过程,海洋环境噪声场不是一成不变的,尤其是随着航运业的发展,交通航运噪声对环境噪声的影响更加显著,使近海海域内的环境噪声较之前发生较大变化,近海环境噪声日益成为人们关注的重点。近年来的研究发现,低频段海洋环境噪声级呈上升趋势,和经典的Wenz谱相比,在不同频段内有着小到1~3 dB、大到10~12 dB的增加[2]。
目前水声设备向着低频、远程方向发展,作为低频段海洋环境噪声的主要噪声源,海上航船对噪声场的影响不容忽视。目前学界对风成海洋噪声的研究较多,而对于低频段的海洋环境噪声涉足相对较少。因此本文针对浅海环境,提出一种计算航船噪声对海洋环境噪声贡献的算法,主要关注频段为 50~400 Hz,并利用实验数据对该算法进行了验证。
1 理论推导
1.1 声传播模型
海洋环境下声传播模型主要包括波数积分模型、简正波模型、射线模型、抛物方程模型、有限差分模型(有限元模型)[3]。本文选用了抛物方程模型对声场进行计算。
在研究低频段海洋环境噪声时,对于低频、浅海条件,射线模型不再适用,因此本文采用了抛物方程(Parabolic Equations,PE)模型[3]。此方法可以较为精确地计算声压。
抛物方程法是一种近似算法,将声压方程近似为抛物线型方程。采用柱坐标(r,φ,z)进行推导,等密度介质的三维亥姆霍兹方程为
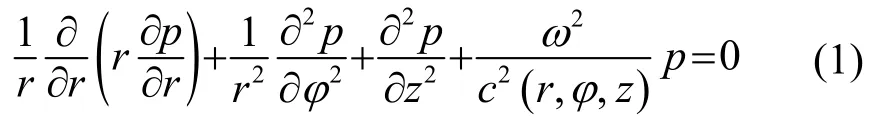
假设方位对称,可得到:

式中,p(r,z)是声压,k0=ω/c0是参考波数,n(r,z)=c0/ c(r,z)是折射率。
根据Tappert的研究[4],可以假设式(2)的解满足以下形式:
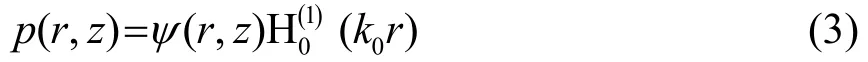
将式(3)代入式(2),并作远场近似,即 k0r≫1,可得到:
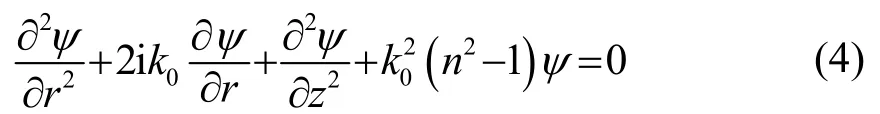
引入近轴近似:

最终得到标准的窄角抛物线方程:
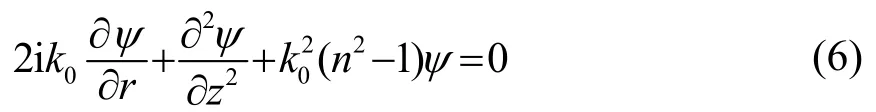
为求解式(6)所示的PE方程,推导一系列基于算子形式的抛物波方程。首先定义如下算符:

则式(6)可重写为
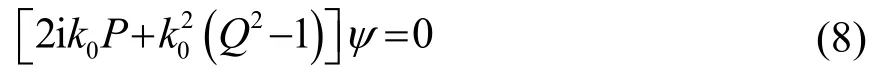
这里,求解方程的关键在于对Q算符的数学近似。距离相关声学模型(Range-dependent Acoustic Model,RAM)程序作为一种声场计算程序,它基于分步帕德(Padé)算法,对抛物方程组进行求解。在数学中,Padé近似值是一个给定阶数的有理函数对一个函数的“最佳”近似值[9-10]。应用到实际场景时,将声速梯度、海底声速、海底底质密度和吸收系数等环境参数作为输入,利用RAM程序对声场进行计算,得到不同频率声波在特定海洋环境下的声传播特性。本文将航船视为点源,利用 RAM程序计算浅海中航船的传播损失LT。在海洋环境中,声波在传播过程中的损失主要包括[5]:扩展损失、吸收损失、散射、海底反射损失。在这里假定海面为理想界面,不考虑海面的散射。
通常深海环境下可不考虑海底反射损失。但在浅海环境下,除了扩展损失和海水吸收损失,海底反射损失是一项关键因素。本文关注的是浅海海洋环境,因此在利用 RAM进行计算时,必须将海底损失考虑在内,以得到声波传播过程中的总传播损失。
在利用RAM程序计算声场时,还要注意以下两点[3]:
(1)首先要建立一个在深度上有限的求解区域(0≤z≤zmax),它包括实际物理域(海水和海底)及“海绵”层,“海绵”层是为了避免在下部计算边界上产生附加反射,减少误差;“海绵”层底部深度zmax=4H/3,其中H是传播路径上实际物理域的最大深度。
(2)其次要选择合适的网格尺寸(Δr,Δz),Δr为距离步长,Δz为深度步长。在浅海环境中,深度步长需满足:Δz≤λ/4,其中λ是声波波长;距离步长需满足:2Δz≤Δr≤5Δz。为了获得精确的数值解,唯一的办法是按一定规则逐步减小Δr和Δz,对解(传播损失)的收敛性仔细的检验。若Δr和Δz的值设置不合适,可能会导致不同频率下的传播损失计算值产生误差,因此需要针对不同频率分别进行收敛性检验。
1.2 航船噪声计算方法
为了研究海洋环境噪声场的水平方向分布,以接收点为中心,将海洋划分为若干楔形区域,如图1(a)所示。图1中xOy平面代表海面;从海面开始往下直至接收点所在平面,接收点记为R,D为接收点的深度。在z=D处取垂直于z轴的截面,并绘制扇区分布如图1(b)所示。航船位置按划分的扇区分组,扇区均匀分布,每个扇区作为一个方向。例如,划分间隔若为2°,整个区域将划分为180个扇区。扇区划分越密,误差越小。扇区截面的半径由选取的计算范围决定,选取的范围越大,半径越大,黑色散点代表航船在扇区截面的投影。利用本文算法计算时,可提前计算目标海域的声场,得到传播损失随传播距离的变化,结合传播损失和航船声源级确定扇区的半径。

图1 楔形区域及扇区划分分布图Fig.1 Division map of wedge-shaped area and sector area
对某一个扇区的接收声压pR,可按式(9)和式(10)进行计算[6]:

式(10)中,m表示航船序号,m=1,2,3,··,M,M为该扇区内船的数量,各个符号含义如下:
(1)rm为该扇区内序号为m的航船到接收点的距离;
(2)rc为该扇区内航船与接收点的最大距离,分别计算该扇区内的每艘航船到接收点的距离,取最大值即为rc;
(3)Lsm是该扇区内航船 m在某一频率下的声源级,计算方法在1.3节讨论;
(4)ωm指该扇区内航船m对应的权重系数,由式(11)得到:

按式(9)、(10)计算得到不同频率的接收声压pR后,进而可得到接收点处水听器的接收声压谱密度DRL(f)[7],计算公式为

式中:参考声压pref=1μ Pa。对其他扇区可重复进行上述计算流程。
1.3 航船噪声源
对航船噪声源的模型,目前仍缺乏合适的数学与物理描述,一般仍采用经验公式或半经验公式描述。Ross[1]提出典型商船辐射噪声的回归公式,后来Hamson[7]更新了Ross的航船辐射噪声的回归方程,航船辐射噪声功率谱密度如式(14)[1,7]所示:
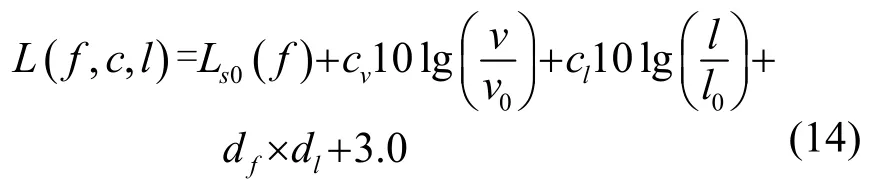
式(14)各参数代表的意义如下:
(1)cv和cl分别代表航船速度和航船长度的罗斯幂律系数,cv=6,cl=2。
(2)v,l分别是船舶的速度和长度。v0和l0分别是航船参考速度和参考长度,v0=12 kn(1kn=1.852 km·h-1)、l0=300 ft(1ft=0.3048 m)。
(3)df是随频率变化的修正量,由式(15)给出,频率f的单位是Hz[7]:

(4)dl是随航船长度变化的修正量,由式(16)给出:

(5)Ls0(f)是仅与频率相关的分量,由式(17)给出[7]:
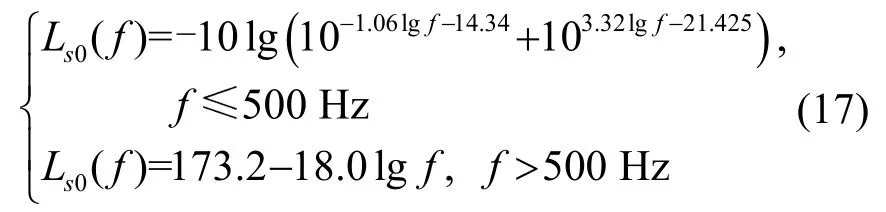
利用式(14),结合获取的航船自动识别系统(Automatic Identification System,AIS)数据(AIS数据将在2.1节进行说明),可以得到某一频率的航船辐射噪声功率谱密度Ls。
2 AIS数据介绍及预处理
2.1 AIS数据介绍
利用第1节构建的算法,结合AIS数据,进行了仿真计算。航船的位置、航速、船长等信息来源于船舶自动识别系统(AIS),以上数据作为算法的输入,需要进行一定的预处理,在本节中将对此进行阐述。
图2所示的是仿真所考察的航船AIS数据分布范围示意图,其中中心点经纬度为[123.16°E,30.02°N],4个顶点的坐标分别为:[122.16°E,29.02°N]、[124.16°E,29.02°N]、[124.16°E,31.02°N]、[122.16°E,31.02°N]。该区域经度跨度、纬度跨度均为2°。
航船AIS数据主要包括船名、海事移动服务识别参数(Maritime Mobile Service Identity,MMSI)、船舶类型、船舶状态、船长、船宽、吃水、航向、速度、经度、纬度、时间戳等信息。文中船名和MMSI号已被隐去,必要时以手动编号代替。

图2 航船AIS数据分布范围Fig.2 Distribution range of ship AIS data
表1中代表的是某航船在两个时刻对应的航船信息,包括船长、船速、吃水深度、经纬度和记录时间等,在两个时间点的航速和航向不同。表中UTC代表格林威治标准时间,与北京时间相差8个小时,“UTC+8”即为北京时间。

表1 某航船AIS数据Table 1 AIS data of a ship
2.2 数据预处理
对于得到的AIS数据进行预处理,包括:
(1)剔除存在明显错误的数据,剔除航船中发动机已关闭的船舶;
(2)筛选符合时间范围内的数据,利用 Matlab软件保存到数据库;
(3)利用航船的船速、航向对数据进行插值处理,作为数据的补充;
(4)查看地图可发现,岛礁是一个必须考虑的因素,在某一个时刻下,如果航船与接收点的连线上出现了岛礁,可能会出现衍射(绕射)。现已证明,声衍射的强弱和障碍物的大小与声波波长的比值密切相关,其关系式为

式中:k为声波的波数;f、c、λ分别为声波的频率、速度和波长;a是代表障碍物尺度的量,如为球体a就代表球体的半径。当ka≫1时衍射很弱,声波几乎只是沿着直线传播以至于被球体挡住传播路径而在其背面形成明显的声影。当岛礁尺寸满足ka≫1时,则应将此艘航船予以剔除。
经预处理得到航船分布和各艘船的信息后,依据算法,可独立计算各扇区内船舶辐射噪声级谱密度DRL(f)。
3 仿真计算
3.1 仿真水体环境
水体环境参数参考某次海洋环境噪声实验。该次测量点位于图2所示海域范围内,水深约70 m,声速梯度由电导率、温度、深度(Conductivity,Temperature,Depth,CTD)系统测得,如图3所示。用侧扫声呐测量海底,发现该海域海底较为平坦。同时通过对海底底质的采样,可知其主要成分接近粉砂质砂。
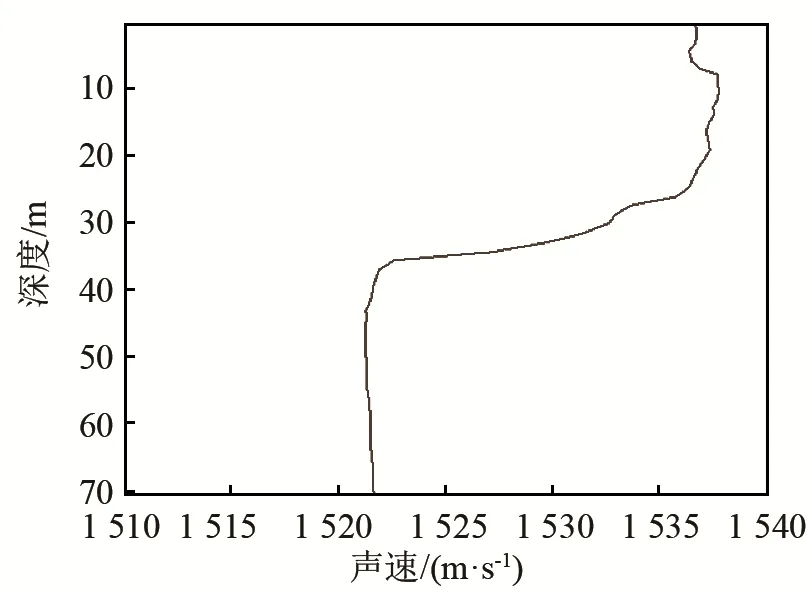
图3 实验海域声速梯度剖面图Fig.3 Acoustic velocity profile in the experimental area
3.2 水平方向分布分析
取某一时刻海域内的航船数据作为输入,包括航船经纬度、长度、速度、吃水深度。预处理之后,运用1.3节的方法进行仿真计算。图4即为该时刻预处理之后的航船位置分布图,将此位置分布下的航船数据作为输入,进行航船噪声的仿真计算。
按1/3倍频程计,选定中心频率,分别计算频段内若干频点的功率谱密度值,并取平均得到的结果如图5所示。
从图5中可以看出:
(1)在不同频率下,航船噪声功率谱密度水平分布图形状不同。这是由于不同频率的声源在实验海域内的传播损失曲线不同:给定两个不同频率、相同声源级的声源,两者的传播损失随距离的变化不同,导致不同频率下的水平分布图不同。

图4 某一时刻的航船位置分布图Fig.4 Distribution of ship positions at a certain time


图5 不同中心频率航船噪声功率谱密度的水平方向分布图Fig.5 Horizontal distributions of the ship noise power spectral density at different center frequencies
(2)图5(a)~5(j)中:6°~12°、32°~36°、50°~52°、70°~72°、152°~154°、-152°~-122°、-118°~-30°、-18°~-16°和-12°~-8°方向的水平分布图为“包络”,其余为“线谱”。
进一步分析数据,计算方法不变,从图5(a)~5(h)中提取相应方向的数据形成的-116°方向、128°方向、-36°方向、34°方向上在这一时刻的航船信息,结果如表2所示。表2说明在这一时间点某一方向上有几艘船,以及每艘船的船长、船速、吃水深度信息,在-116°方向上有两艘船:A1,A2;在-36°方向上有四艘船:B1,B2,B3,B4;而在128°方向和34°方向上均只有一艘船,分别是D和E。
4个方向上航船噪声功率谱密度随频率的变化趋势如图6(a)~6(b)所示。
依频率提取多个方向上的数据,得出如下结论:
(1)若扇区内存在多艘航船,各艘航船的航行状态不同,受到航船噪声叠加的影响,不同方向上航船噪声功率谱密度随频率的变化趋势差别较大,如图6(a)、6(b)所示。
(2)若扇区内仅存在一艘航船,则航船噪声功率谱密度随频率的变化趋势较为稳定,图形走势基本一致,如图6(c)、6(d)所示。

表2 不同方向上的航船信息Table 2 Ship information in different directions
3.3 功率谱密度分析
采用本文算法,航船AIS信息输入和水体环境参数与3.1节相同,得到了某一时刻的航船噪声功率谱密度仿真结果。该时刻为2016年7月6日9时0分0秒,对不同方向的噪声功率谱密度取平均,仿真结果如图7中的星点所示,计算的频点包括50、63、80、100、125、160、200、250、315、400 Hz。
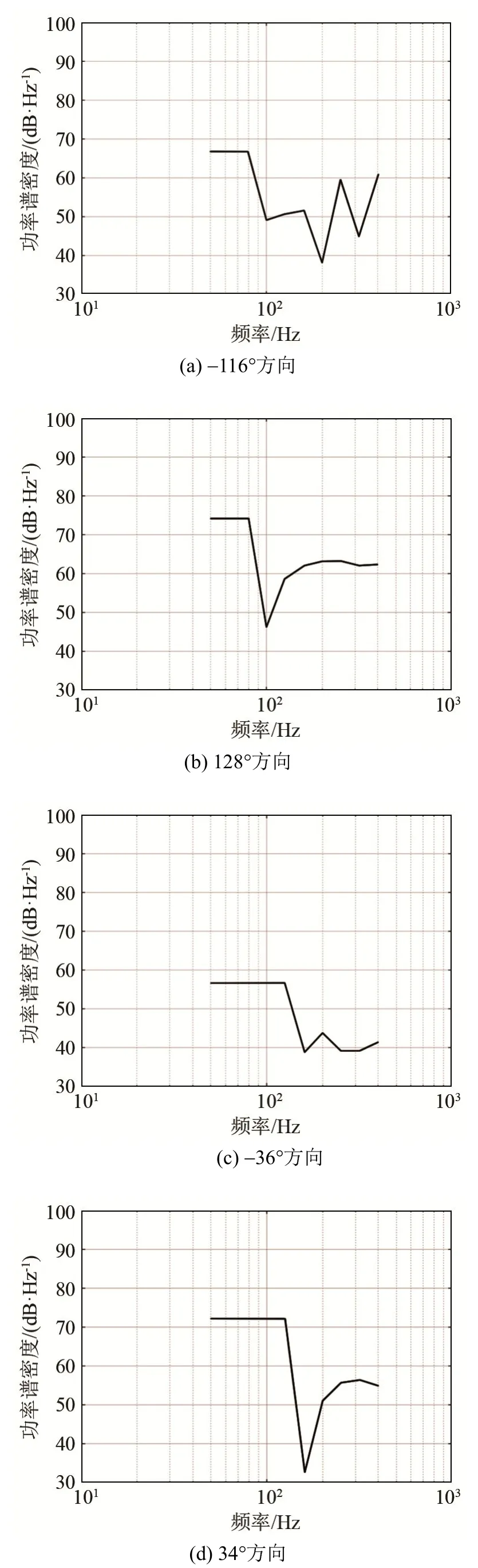
图6 不同方向航船噪声功率谱密度Fig.6 The ship noise power spectrum densities in different directions
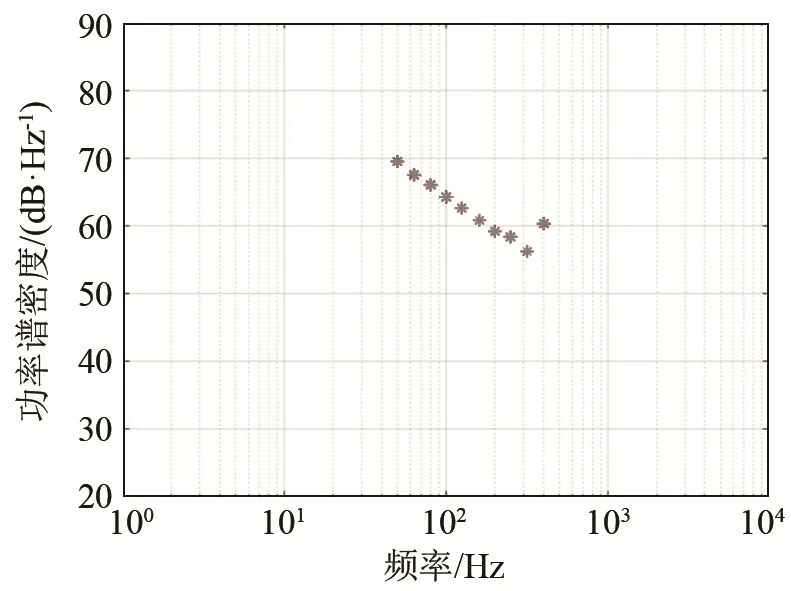
图7 对某一时刻不同方向航船噪声功率谱密度取平均的仿真结果Fig.7 Simulation result of the ship noise power spectral density averaged in different directions at a certain time
对于海洋环境噪声的研究,Wenz噪声谱级图是一个重要的参考。它是由Wenz等[8]总结出的经典海洋环境噪声功率谱级图。经典Wenz噪声谱级图中包含了航船、风、降雨、地震和爆炸等不同因素对环境噪声的贡献,如图8所示:横坐标代表频率(以倍频程记,频率从1 Hz~100 kHz),纵坐标代表海洋环境噪声谱级。Wenz噪声谱级图中,不同因素贡献的噪声频段不同,图中各曲线代表的影响因素如表 3 所示。航船对噪声的贡献主要是10 Hz~1 kHz频段,图8中描述了强航道、浅海通常航道、深海通常航道等条件下的噪声谱级。
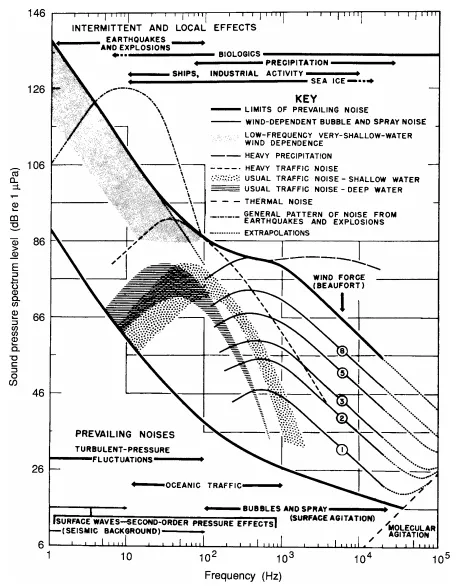
图8 Wenz噪声功率谱级图[8]Fig.8 Wenz noise power spectrum diagram[8]
为了验证本文算法的可靠性,将Wenz噪声谱级图中描述浅海通常航道的曲线取出,与图7所示的仿真计算值同时绘制在图9中。图9中Wenz曲线 1、2分别代表浅海通常航道(Usual Traffic Noise-Shallow Water)的上、下限曲线。由图9可以看出,仿真计算值与描述浅海通常航道的曲线2较为符合,在浅海通常航道的上、下限曲线之间,这也与水听器和航船距离较远这一事实符合。实验所用水听器为无指向性水听器,布放位置为图4中的接收点位置,深度为 41.03 m,水听器与航船的距离从36.69~147.46 km不等。

表3 Wenz噪声功率谱级图说明Table 3 Description of Wenz noise power spectrum diagram
为了进一步验证算法的可靠性,对实验数据进行了分析。图10中连续曲线代表的是在2016年7月6日8时59分30秒~9时30秒的时间段内,实测数据的1/3倍频程功率谱密度。由图10可见,在100~400 Hz频段内,仿真值与实验值较为符合。
与图 10不同,现选取 10个时间点(间隔为1 min),对10个时间点重复上述计算,并取平均,结果如图11中星点所示。图11中的实验值是对共计10 min长度的实验噪声数据进行分析得到的。由图10、11可以发现,其结果与图10中星点代表的仿真计算值结果较为一致,在100~400 Hz频段内两者较为符合。
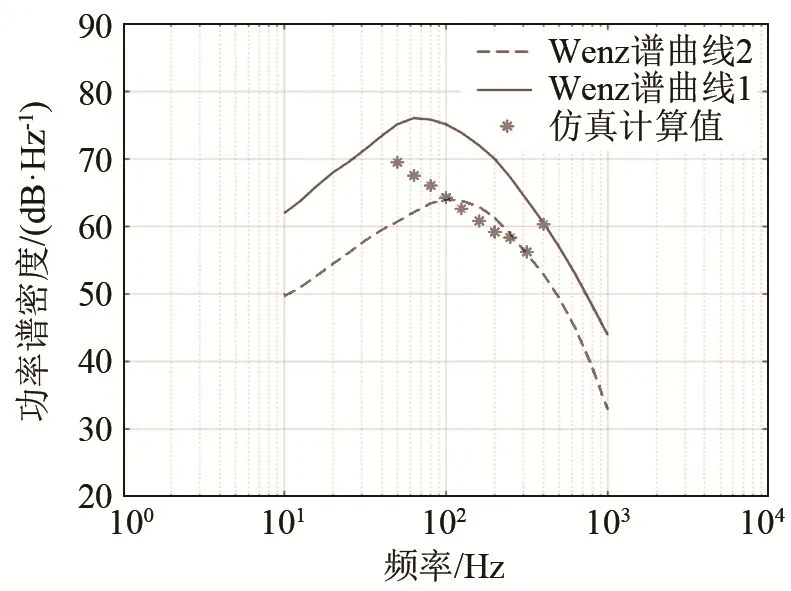
图9 某一时刻航船噪声功率谱密度仿真结果(图7)与典型浅海航道的Wenz谱曲线对比Fig 9 Comparison between the simulation result of ship noise power spectral density(Fig.7)and the Wenz spectrums in typical shallow sea channels
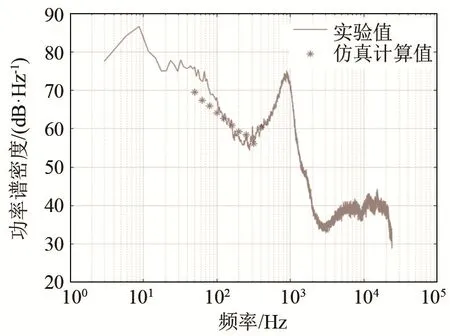
图10 某一时刻航船噪声功率谱密度仿真结果(图7)与实验值对比Fig.10 Comparison between the simulation result of ship noise power spectral density(Fig.7)and the experimental values

图11 航船噪声功率谱密度仿真值(某一时间段内取平均)与实验值对比Fig 11 Comparison between the simulation result of ship noise power spectral density(averaging over a period of time)and the experimental value
本文中 50~400 Hz频段内的仿真结果与经典Wenz谱总体上较为符合,在Wenz曲线浅海通常航道的上下限曲线之内。但50~100 Hz频段内的仿真结果略低于实测环境噪声数据。分析实验海域附近环境发现,由于实验海域为近海,环境噪声源种类繁多,噪声源除了航船以外,还有工业活动、潮、涌、浪、远处风暴等,并且这些声源对低频段的影响较大,这也是误差产生的原因之一。
4 结 论
本文提出了一种计算航船对近海海洋环境噪声贡献的算法。利用本文算法,结合AIS数据和实际海域水文参数,可获取接收点处航船噪声的水平方向分布特点,并可初步定量分析航船噪声对海洋环境噪声的贡献。本文主要关注的频段为 50~400Hz,理论分析和数值计算均反映出了由于航船的非均匀分布,噪声场在不同频率下呈现明显的非均匀分布特征这一特点。对噪声功率谱密度进行了定量分析,并通过与经典Wenz谱和实测噪声数据进行比对,在约50~400 Hz时仿真值和实验值吻合较好,验证了算法的可靠性。同时,在应用时需要尽可能多地获取环境参数,以降低数值计算时的误差。

