工程卡车行驶引发地面振动特性研究

时 刚， 田新涛

(郑州大学 土木工程学院，河南 郑州 450001)

0 引言

近年来，随着城市工程建设的迅猛发展，重载工程卡车作为工程运输的重要方式，频繁穿梭于城市道路中，其产生的振动和噪音对邻近建筑物以及人们的生活影响也越来越严重，国际上已把交通振动污染列为“七大公害”之一[1]。研究该振动的传播规律及变化形式，可为控制该振动提供依据和参考。

国内外的学者对交通荷载引起周围地面振动响应问题进行了深入研究，取得一定的成果。贾宝印等[2]采用现场实测的方法，得出重载卡车引起附近地面振动以垂向为主；秦林等[3]基于实测数据分析，得出近振源区域车辆垂向振动衰减速率明显高于远振源区域，但未研究横向振动规律；申永刚等[4]指出场地对振动波的传播以及车辆和道路之间的动力作用是一个十分复杂的过程，许多影响因素具有很强的随机性；城市部分道路由于年久失修，路面不平引起的振动问题最为普遍，Hajek等[5]和OECD[6]提到随机路面不平整引起的交通动荷载比静荷载要大大约15%，特定的路面不平整引起的动荷载比静荷载要大50%～80%。

然而上述研究多以实测为主，且实测时各种因素均具有较强的随机性，难以准确反映各因素的影响关系。基于此，笔者采用数值模拟的方法，对不平路面重载卡车行驶引起周围地面振动问题进行研究，首先结合D′Alembert原理，建立整车七自由度运动微分方程；利用FlexPDE软件求解出车辆对地面的激励，并将此激励通过ABAQUS二次开发，施加于土体有限元模型上；在此基础上，研究了车辆引起地面振动的一般规律，并讨论了车速、载重、路面特性等因素对振动传播的影响，结果可为相关部门研究和控制该振动提供依据和参考。

1 数值模型建立

车辆行驶过程中，车轮作用在地面的激振力经土体向周边传播，从而引发地面振动。因此，笔者在建立车辆和路面动力分析模型时，以车辆荷载和大地两个子模型进行分开建模。

1.1 车辆荷载模拟

目前来说，车辆荷载的模拟方法很多，如将车辆系统视为二自由度四分之一汽车悬架模型[7]，四自由度二分之一车辆模型[8]以及考虑车身上下运动和俯仰、侧倾转动等三自由度和车轮上下运动等四自由度的七自由度整车模型[9]。前两者可以较真实地反映车辆垂向运动，但不能反映水平向运动情况。考虑到地面横向振动不容忽略，故笔者基于达朗贝尔原理，以某型号混凝土工程卡车为建模研究对象，将车身、车轴和车轮视为刚体，车身悬架、车轮表示为弹簧和阻尼器，建立整车七自由度物理模型如图1所示，整车系统参数含义如表1所示。

图1 整车七自由度物理模型Figure 1 Vehicle seven-degree-of-freedom model

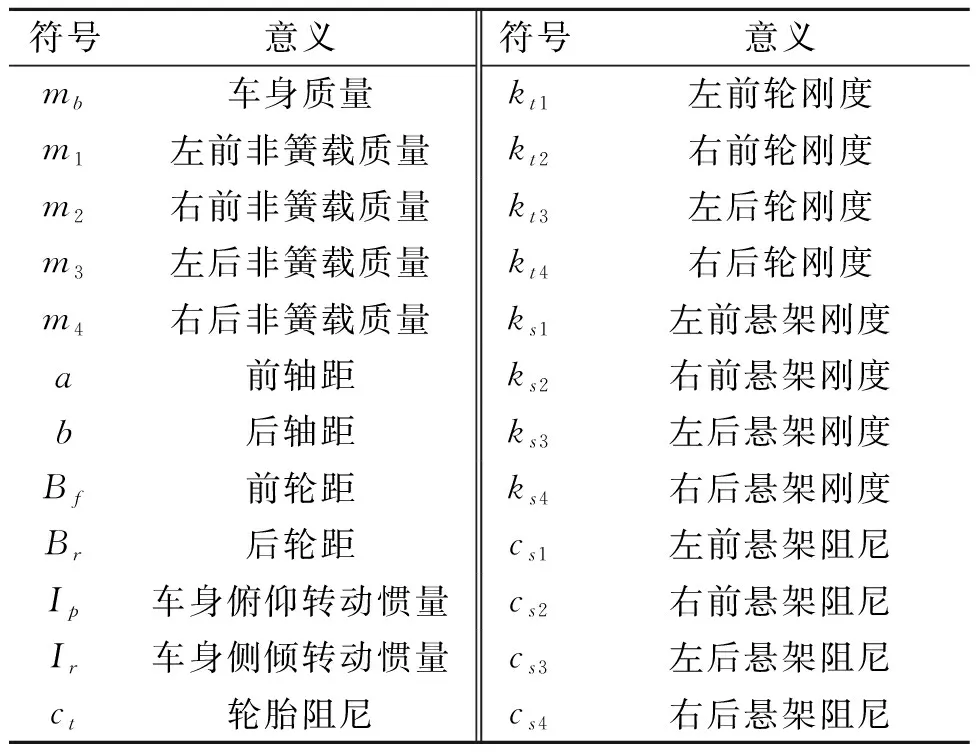
表1 整车系统参数Table 1 Vehicle system parameters

其中zb为汽车质心垂直位移；z1、z2、z3、z4分别为前后4个车轮的垂直竖向位移；zb1、zb2、zb3、zb4为前后4个车轮中心处车身端点的垂直位移；θb为车身俯仰角位移；φ为车身侧倾角位移。

根据汽车动力学，车辆在俯仰角和侧倾角较小时，车身4个端点处的垂向位移有如下关系：

(1)

因此，得出车身质心处的垂向运动方程：

(2)

车身俯仰运动方程：

(3)

车身侧倾运动方程：

(4)

其中4个非簧载质量的垂向运动方程：

(5)

同时将车轮路面激励q视为正弦路面不平整函数，即

q=B0sin(2πvt/L0),

(6)

式中：B0为路面不平整幅值，m；v为车辆速度，m/s；L0为路面不平整波长，m。

车辆轮胎对地面的作用荷载由静荷载和动荷载两部分组成，假设G为车辆静态荷载，卡车轮胎对地面激励F为：

(7)

1.2 路面-地基有限元模型

基于车辆对地面的荷载表达式(7)，利用FlexPDE软件求解出作用激励，作用激励的施加采用在ABAQUS中二次开发的Dload子程序完成。Dload子程序可以根据用户需求，在ABAQUS中定义随时间和空间位置或其他变量变化的复杂荷载，因此常用于实现移动变化荷载的施加。将作用荷载激励输入子程序中，并施加于模型道路有限单元上。

工程卡车引发地面振动的时长相比列车振动往往较短[10]，结合文献资料及多次数值模拟经验，模拟车辆振动时长为2 s，模型X×Y×Z=40 m×80 m×20 m，其中X轴为行车方向即道路纵向，Y轴为道路横向。道路路面参数如表2所示，同时假设地基土体为单一均质土层，采用莫尔-库仑本构，建立ABAQUS大地三维有限元实体模型如图2所示。

表2 道路土体计算参数Table 2 Road soil calculation parameters

图2 大地三维数值模型示意图Figure 2 Schematic diagram of the three-dimensional numerical model of the earth

模型四周铰结，底面固定。在实际工程分析中，土体往往视为半空间无限体模型，而ABAQUS中建立的土体模型为有限模型，在模型四周及下表面施加黏弹性人工边界[11]，使模型计算趋于合理。

1.3 计算模型参数及验证

根据多次现场实测观察，城市道路中工程卡车多为三一重工C8型号，容积为7.99 m3的混凝土搅拌车，最大载重31 t，选取车辆计算参数[12]如下所示：

mb=21 260 kg,m1=m2=220 kg,

m3=m4=1 500 kg，

Ip=3×105kg·m2,Ir=0.6×105kg·m2,

ks1=ks2=2×106N/m，ks3=ks4=5×106N/m，

cs1=cs2=5 000 N·s/m，cs3=cs4=4 000 N·s/m,

kt1=kt2=1.73×106N/m，kt3=kt4=4.6×106N/m，

ct1=ct2=1 200 N·s/m，ct3=ct4=4 300 N·s/m，

a=1.48 m，b=2.02 m，Bf=Br=1.9 m。

假设车轮与道路接触面积按矩形处理，矩形面积为0.3 m×0.4 m，车速为v=40 km/h；郑州市城市道路多为典型沥青道路路面，根据现场实际工况，模拟道路不平整系数B0=0.03 m，路面波长L0=6 m，并参考文献[7]给出沥青道路参数及场地地基土体参数如表2所示。

本次现场实测数据的采用意大利MOHO公司生产的地脉动仪TROMINO©采集完成，图3为现场实测时使用的地脉动仪仪器。

图3 TROMINO©地脉动仪Figure 3 TROMINO© ground pulsometer

图4和图5所示为实测40 km/h运行车辆，距离道路中心20 m处，竖向和横向振动加速度值与模型计算结果的比较图像。

图4 竖向振动加速度时程对比图Figure 4 Comparison of vertical vibration acceleration time history

图5 横向振动加速度时程对比图Figure 5 Comparison of lateral vibration acceleration time history

本次模型计算取值在时间历程为1 s 时刻，笔者着重关注车辆经过时的振动响应情况，通过观察图4和图5可知，模型的竖向和横向振动计算结果与实测值较为接近，且在0.75～1.25 s车辆经过区段，振动时程曲线与实测曲线在数值和波形上较为接近，说明重载车辆荷载、道路路面及土体参数的选择基本上与实际情况相符，计算与实测对比结果能满足笔者的研究需求，模型建立较为合理。

2 车辆引起的地面振动分析

振动加速度级常用于表征振动强度的数值指标，将数值计算中振动加速度换算为振动加速度级，以便分析工程卡车引起地面振动的传播规律，文献[13] 给出了振动加速度级计算公式如下：

VAL=20log(arms/a0),

(8)

式中：VAL为振动加速度级，dB；a0为基准加速度，10-6m/s2；arms为振动加速度有效值，m/s2。

振动加速度的有效值计算如下所示：

(9)

根据多次数值计算结果，道路纵向方向振动变化规律与竖向类似，仅数值大小存在差异，且地面振动主要体现在横向和竖向，因篇幅限制，笔者主要讨论地面竖向和横向振动变化情况。

2.1 速度对地面振动特性影响

车辆固定速度为v=40 km/h，为研究速度增大对地面振动的影响，将速度增大到50 km/h、70 km/h。作出竖向和横向振动加速度级随振源距离变化曲线如图6和图7所示。

图6 竖向振动加速度级随距离衰减Figure 6 Vertical vibration acceleration level with distance attenuation

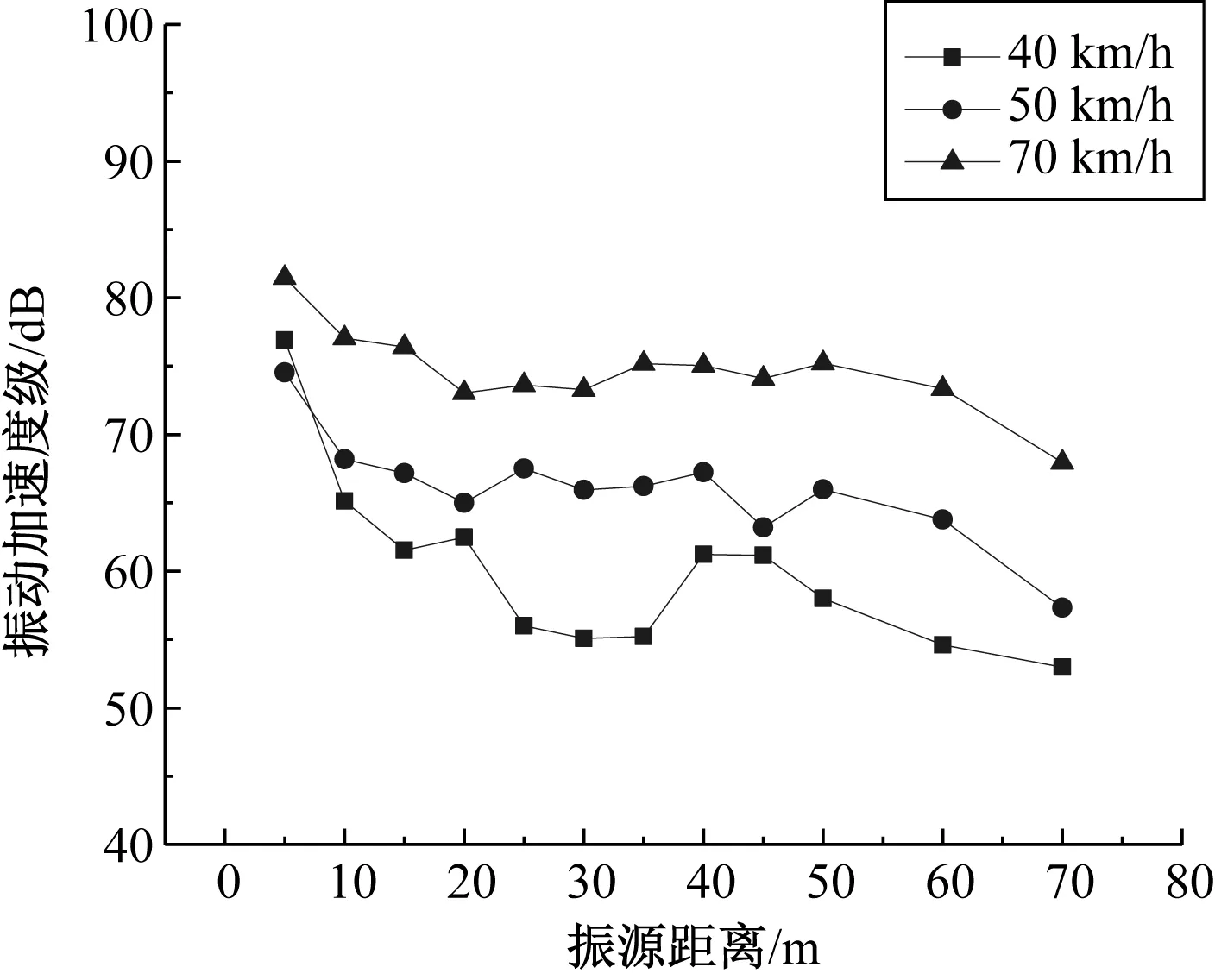
图7 横向振动加速度级随距离衰减Figure 7 Transverse vibration acceleration level with distance attenuation

首先分析典型情况时(速度固定为v=40 km/h)地面振动随振源距离增加的情况。由图6可知，竖向振动在近振源处衰减较快，在远振源区域，衰减逐渐趋于平缓，同时远处振动曲线幅值变化不大；横向振动在近振源区域衰减速率较快，远处衰减趋于平缓。

地面振动强度随着速度的增加而增大，速度越大，该点的振动响应越显著；从各向振动强度来看，地面竖向振动加速度级大于横向，且在数值上始终有竖向大于横向,故重载卡车引起地面振动以竖向为主。

观察竖向和横向振动在v=40 km/h时的振动曲线。可以看出，在距振源为40～50 m时,振动数值有所增大，这可能是振动波在地层中多次反射叠加增大的结果。

随着速度增大，振动传播特性不变，但幅值变化明显，因此城市道路中采用限速是控制该振动传播的重要方式。

2.2 载重对地面振动特性影响

图8和图9分别为车速固定v=40 km/h时，其他参数保持不变，载重由100 kN增加到200 kN、300 kN和550 kN引起地面竖向和横向振动响应的计算曲线图。

图8 竖向振动加速度级随距离衰减Figure 8 Vertical vibration acceleration level with distance attenuation

图9 横向振动加速度级随距离衰减Figure 9 Transverse vibration acceleration level with distance attenuation

由图8和图9可知，载重变化时，地面竖、横向振动具有较大的波动性，这与载重变化引起车辆行驶产生的动荷载的波动性以及路面自身不平整的周期性密切相关。基于当前研究，载重变化引起地面振动的作用方式十分复杂，但仍是影响振动的重要因素，载重较低时，振动幅值曲线较为接近，载重增大，振动幅值有显著提高。因此控制车载重量是控制该振动的有效手段。

2.3 路面特性对地面振动特性影响

针对路面特性对地面振动的影响，选取路面波长为变化参数，作出路面波长由3 m增加到6 m、12 m、18 m和24 m时，竖向和横向振动加速度级随振源距离变化的关系图，如图10和图11所示。

图10 竖向振动加速度级随距离衰减Figure 10 Vertical vibration acceleration level with distance attenuation

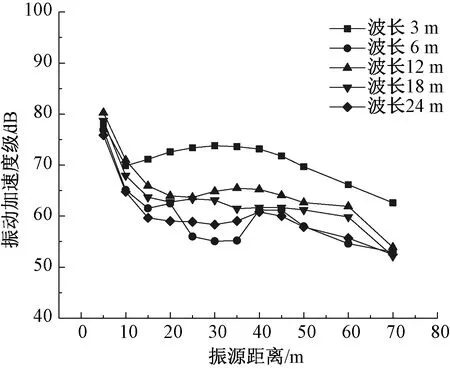
图11 横向振动加速度级随距离衰减Figure 11 Transverse vibration acceleration level with distance attenuation

分析图10和图11可知，随着路面波长的增大，路面波动周期增大，路面趋于平整，地面振动影响逐渐降低；当波长为12 m时，此时由于车辆行驶产生动荷载的波动性与正弦周期路面的叠加共振往往会使地面产生振动放大现象。

3 结论

重载卡车行驶对周围地面的振动响应影响是比较复杂的，目前对其传播规律的认识和掌握仍需要进行大量的现场试验和理论分析研究。通过对重载卡车行驶引发地面振动问题进行模拟和计算，得出以下结论可供相关部门研究和控制该振动参考：

(1)近振源范围内,地面竖向和横向振动衰减速率明显高于远振源区域，重载卡车引起地面振动以竖向为主，但横向振动同样不可忽视。

(2)固定速度40 km/h时,车辆横、竖向振动数值为55～80 dB，速度增大到70 km/h时，振动幅值显著提高。在城市道路中，可以采用限速的方式来控制该振动影响。

(3)载重在100～300 kN之间变化时，地面振动增大不太明显，当载重550 kN时，振动强度有显著提高，因此限制超载是控制振动放大的重要方式。

(4)路面波长从12 m增加到24 m时，路面逐渐趋于平整，振动数值有所降低，特定波长12 m时，车辆动荷载与路面发生共振会出现振动放大现象。