液压互联悬架参数全局灵敏度分析与多目标优化
张农 王少华 张邦基 谭博欢


摘 要:液壓互联悬架(Hydraulically Interconnected Suspension,HIS)系统的参数匹配直接影响着其动态性能. 为提升HIS系统的综合性能,对抗俯仰抗侧倾HIS系统的主要参数进行了全局灵敏度分析和多目标优化. 建立7自由度“机-液”耦合整车频域动力学模型,以四轮随机路面为输入,以反映车辆平顺性、稳定性和抗俯仰抗侧倾性能的各项性能指标为目标函数,采用Sobol指数法对HIS系统参数进行了全局灵敏度分析,获得影响HIS系统性能的关键参数. 基于参数灵敏度分析结果,使用NSGA-II算法对HIS系统进行了多目标优化. 结果表明:管路阻尼阀和蓄能器阻尼阀线性损失系数对车辆各性能有较大影响,参数间的交互效应对车辆抗侧倾性能影响明显.优化后,通过权重系数法选取的优化结果表明,车身质心处加权加速度均方根值降低20.95%,俯仰角加速度均方根值降低12.95%,侧倾角加速度均方根值降低8.05%,轮胎动载荷均方根值均值降低11.17%. 通过参数灵敏度分析和多目标优化,可以显著提升HIS系统的综合性能.
关键词:液压互联悬架;汽车悬架;灵敏度分析;多目标优化;遗传算法
中图分类号:U463 文献标志码:A
Global Sensitivity Analysis and Multi-objective Optimization
of Hydraulically Interconnected Suspension Parameters
ZHANG Nong1,2,WANG Shaohua1,ZHANG Bangji1?,TAN Bohuan1
(1. State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body,Hunan University,Changsha 410082,China;
2. School of Mechanical and Mechatronic Engineering,University of Technology Sydney,Sydney 2007,Australia)
Abstract:The parameter matching of the hydraulically interconnected suspension(HIS) system has a critical effect on its dynamic performance. To improve the overall dynamic performance of the system,the global sensitivity analysis and multi-objective optimization are proposed for an anti-pitch and anti-roll HIS system. Firstly,a seven degree-of-freedom vehicle dynamic model is established in the frequency domain. Then,the riding comfort,stability,and anti-pitch and anti-roll performance of the vehicle are evaluated by stochastic road input. In addition,the global parameter sensitivity analysis of the HIS system is presented using the Sobol method to evaluate the influence of each parameter and find out the critical parameters of the HIS system. Furthermore,a multi-objective optimization procedure is proposed to optimize vehicle performance by the NSGA-II algorithm. The result illustrates that the linear loss coefficients of the damping valves on cylinders and accumulators have a significant influence on each performance index,and the interaction effect of some parameters has a great influence on vehicle anti-roll performance. After multi-objective optimization,the optimization result obtained by the weighted coefficient method shows that:the root mean square(RMS) value of sprung mass′s weighted acceleration is decreased by 20.94%;the RMS value of pitch acceleration is decreased by 12.95%;the RMS value of roll acceleration is decreased by 8.05%;the mean value of tire dynamic force RMS value is decreased by 11.17%. Through the global sensitivity analysis and multi-objective optimization,the overall vehicle performance can be improved significantly.
Key words:hydraulically interconnected suspension(HIS);vehicle suspensions;sensitivity analysis;multi-objective optimization;genetic algorithms
平顺性和稳定性是评价车辆性能的重要指标,也是一对相互对立的性能指标. 为了同时提升车辆的平顺性和稳定性,科研人员进行了大量的研究. 液压互联悬架系统(Hydraulically Interconnected Suspension,HIS)能够实现车辆运动模态的解耦,可以针对性地改变车辆的运动状态,对平顺性和稳定性进行协调控制,同时比主动悬架结构简单可靠、成本低,因而受到国内外学者的广泛关注[1-2].
对HIS系统的研究至今已取得很大进展,获得了一系列重要的研究成果. 张农等对HIS系统的数学建模方法和频域、时域分析方法进行了研究,对各工况下的动态响应进行了仿真分析和试验研究,形成了一套完整的理论成果[3-6]. 为充分发挥HIS系统的性能,对HIS系统参数进行优化匹配设计尤为重要. 参数灵敏度分析和多目标优化常应用于系统的优化设计当中. 参数灵敏度分析可以分析系统参数对车辆各性能的影响程度,减少设计变量[7-8]. 多目标优化可以平衡系统的不同性能需求,使系统可以在最佳状态下工作. 国内外学者对此进行了很多相关研究,Xu等将全局灵敏度分析应用到非线性动力吸振器的结构优化当中[9];Zhu等提出了一种综合灵敏度分析方法[10]; Papaioannou提出一种在车辆悬架系统多目标优化中减少优化目标的方法[11]. 对HIS系
统的参数灵敏度分析和优化也有很多研究,Smith等对抗侧倾互联形式的HIS系统参数进行了局部灵敏度分析,并以舒适性、稳定性指标为优化目标对HIS系统的部分参数进行了多目标优化[12];Saglam等对
装配HIS系统的三轴车平顺性进行了优化[13];周兵等基于模糊灰色關联的灵敏度分析方法和Morris法对抗侧倾互联形式的HIS系统参数进行了灵敏度分析,并以悬架垂直模态和侧倾模态的响应为优化目标进行了参数优化[14-15]. 这些研究多是建立车辆的半车模型,对抗侧倾互联形式的HIS系统进行参数灵敏度分析和优化,未对抗俯仰抗侧倾互联形式的HIS系统展开深入的研究分析.
本文以抗俯仰抗侧倾互联形式的HIS系统为研究对象,建立“机-液”耦合的7自由度整车频域动力学模型,以车辆平顺性、抗俯仰抗侧倾性能和稳定性指标为目标函数,使用Sobol指数法对HIS系统参数进行了全局灵敏度分析,并根据灵敏度分析结果,选取对系统性能影响较大的关键参数作为优化变量,使用NSGA-II算法进行多目标优化.
1 动力学建模
建立7自由度整车模型,其模型示意图如图1所示. 图中:zs为簧上质量质心处垂向位移;θ和φ分别为车身俯仰角和侧倾角;zuij(i = f,r;j = l,r)为轮胎质心处的垂向位移;muij为轮胎质量;ktij为轮胎刚度;车身与轮胎之间通过悬架系统连接,ksij为悬架刚度.
液压缸替代传统悬架中的阻尼元件,通过液压管路、阻尼阀和蓄能器等元件相互连接构成HIS系统. 车辆系统仿真参数如表1所示.
1.1 7自由度车辆动力学方程
使用拉格朗日法进行系统动力学建模. 该模型的机械系统部分为无阻尼振动系统,其拉格朗日方程可表示为:
式中:T为系统总动能;V为系统的势能;Qi为非势力广义力.各项可以表示为:
式中:qij为路面位移输入;zsij为簧上质量与悬架连接处位移,可表示为:
故车辆的动力学微分方程可表示为:
式中:x=[zs θ φ zufl zufr zurl zurr]T;M和K分别为机械系统的质量、刚度矩阵;fh为作动器输出力向量,可表示为fh = Dh P,Dh为系数矩阵,P为压力向量:
fw为路面激励力向量:
式中:zgij = zuij - qij .
1.2 HIS系统方程
HIS系统如图2所示. 该系统由4条回路组成,每条回路通过2个管路阻尼阀、1个蓄能器阻尼阀、1个蓄能器和1个三通接头将两个不同的液压缸上、下腔连接,液压缸的上、下端分别与簧上质量和轮胎相连,在此之间输出作用力. 当车辆转弯时,例如左转,车辆发生侧倾,左侧液压缸被拉伸而右侧液压缸被压缩,这时,回路1和回路4中的压力降低,而回路2和回路3中压力升高,HIS系统产生与车体侧倾方向相反的阻力矩. 同样的,当车辆处于俯仰工况时,HIS系统同样可以通过类似的方式产生阻止车身俯仰的阻力矩.
将HIS系统产生的作用力看作外力施加在簧上质量和轮胎之间,每个液压缸产生的作用力可以表示为:
ij分别是由于液压缸的活塞杆相对运动引起的上、下腔液体的体积流量;qL
ij是液压缸上、下腔之间的泄漏流量,qL
ij)/Rlk,Rlk为泄漏系数;[z] sij是缸体与活塞的相对运动速度.
每条回路由阻尼阀、蓄能器、液压管路组成,每个元件的阻抗矩阵可以通过文献[4]获得,每条回路的阻抗矩阵可以通过回路上各元件的阻抗矩阵相乘获得. 故沿着液体流动的方向,在每条回路的终点处,压力和流量的频域关系可以表示为:
45分别表示管路阻尼阀、液压管路、蓄能器和蓄能器阻尼阀的阻抗矩阵,左上标m表示回路编号. 分解式( 10 )得各腔室之间的压力与流量频域关系的表达式:
式中:s为拉普拉斯复变量;Z(s)为整个液压系统的阻抗矩阵;Q(s)为液压系统流量向量.
1.3 “机-液”整车系统耦合方程
液压缸缸体和活塞的相对运动引起液压缸上、下腔室液体体积流量的变化,反之亦然. 通过机械系统的相对运动和液压系统的体积流量变化将机械系统和液压系统进行耦合,耦合边界条件可表示为:
式中:Dm为系数矩阵.
通过式(5)(11),可以获得“机-液”整车系统耦合动力学方程. 将耦合边界条件式(12)代入系统方程,并转化为状态空间形式:
式中:[X][~](s) = [ xT [x] T]T,为系统状态向量;U(s) 为路面输入向量;特征矩阵A(s)和系統输入系数矩阵B可表示为:
2 车辆平顺性和稳定性评价方法
平顺性是指车辆在行使过程中,保证乘员所处的振动环境具有一定的舒适性和保存货物完好的性能. 根据ISO 2631标准,可通过加权加速度均方根值(WRMS)来反映振动对人体舒适和健康的影响,使用簧上质量质心处的WRMS对车辆的平顺性进行评价,可表示为:
式中:kb = 1;kp = 0.63;kr = 0.4;a wz、a wθ、a w φ分别为簧上质量质心处垂向、俯仰和侧倾的WRMS,通过式(17)计算:
式中:wi为0.5~80 Hz频段内各1/3倍频程频段的频率加权系数;ai为该频段内的加速度均方根值.
车身的俯仰角加速度、侧倾角加速度可以反映HIS系统的抗俯仰、抗侧倾性能,其均方根值(RMS)表示为:
稳定性反映车辆的抗干扰能力,当车辆受到外界干扰(路面不平、侧风、货物或乘客偏载)时,车辆能保持稳定行驶的性能. 悬架动行程(ST)和轮胎动载荷(TD)是评价车辆稳定性的重要指标,在此使用悬架动行程和轮胎动载荷RMS的均值反映车辆稳定性,表示为:
在四轮随机路面输入下,车辆各性能指标的功率谱密度(PSD)可表示为:
H为输入到输出的传递函数,且
式中:Y为系统输出;C为输出系数矩阵;D为直接传递矩阵. Gu为四轮随机路面谱密度矩阵:
式中:B和L分别为车辆轴宽和轴距;v为车辆行驶速度(45 km/h);Gq(f)为单侧路面谱密度:
式中:G0为路面粗糙度(G0 = 5.08 × 10-5 m3);n0为参考空间频率(n0 = 0.1 m-1);k为频率指数(k = 3).
3 HIS系统参数全局灵敏度分析
参数灵敏度分析是识别影响系统性能关键参数的重要手段,能够指导模型优化和提升优化效率. 全局灵敏度分析不仅可以分析单个设计变量对系统输出响应的影响,同时还能够分析设计变量之间交互作用对输出产生的影响. 本文使用Sobol指数法将HIS系统的主要参数作为变量进行参数灵敏度分析,变量及其范围如表2所示.
目标函数选取上文提出的车辆性能各评价指标,故目标函数向量,即系统的输出向量为:
对参数空间进行抽样,获得参数矩阵A和B:
式中:k为变量个数(k = 6);n为抽样次数(n=5 000). 将A和B的第i列互换,获得参数矩阵Ci和C-i:
将参数矩阵A、B、Ci、C-i代入系统模型,获得各参数矩阵的目标函数输出yA、yB、y
C-i. 根据蒙特卡罗法,各设计变量的主效应(一阶灵敏度)指标S
xi和全效应指标ST
xi分别可以表示为:
xi表示单个变量xi对系统输出响应的影响,值越大则影响越大;全效应指标ST
xi不仅包含了设计变量xi的主效应,还包含了xi与其他设计变量之间的交互作用对输出响应的影响,其与主效应指标差值越大,说明交互作用越明显. 经计算,各目标函数对各设计变量的一阶灵敏度指数S
xi如表3所示,全效应指数ST
xi如表4所示.
对比表3和表4可以得出:影响平顺性指标f1的主要参数是Rp,其交互效应的影响很小,其他参数对f1的影响都很小;对车身俯仰角加速度指标f2影响较大的参数为Rp和Ra,其交互效应的影响较小,其他参数对f2也有一定影响;各参数对车身侧倾角加速度指标f3都有较大的影响,且除Ratio S外,其他参数的交互效应影响都很明显;对悬架动行程f4影响较大的主要参数是Rp,其交互作用的影响较小,其他参数对f4的影响很小;对轮胎动载荷f5影响较大的主要参数为Rp,其交互作用的影响较小,其他参数对f5也有一定的影响. 综上:Rp对各目标函数都有较大的影响,其次为Ra;Pm、Pp、Vp,对不同的目标函数影响程度不一;Ratio S相较于其他参数,对各目标函数的影响都很小.
4 多目标参数优化
通常一个多目标优化问题可以描述为:
式中:f(x)为目标函数向量;x为优化变量向量;hi(x)和gi(x)分别为等式约束和不等式约束;X为优化变量的定义域. 选取上文提出的性能指标作为目标函数,建立目标函数向量如下:
根据蓄能器的工作需求,工程应用中液压系统的平均压力要高于蓄能器的预充压力,故设置不等式约束:
从参数灵敏度分析结果可以看出,Ratio S对各目标函数的灵敏度都比较小,且在工程实际应用中,液压缸上、下腔截面积比有相应的标准,故在优化过程中将其值设置为定值,只对其他参数进行优化. 优化变量的取值范围如表2所示,优化变量向量如下:
NSGA-II算法是一种常用的多目标遗传算法,具有运行速度快,解集收敛性好的优点,常应用在多目标优化当中. 该算法通过非支配排序对种群进行适应值分级,使用拥挤度距离保证种群多样性,通过精英策略选择父代种群,并通过遗传和变异产生子代种群,如此循环直到达到设置的进化代数. 优化中使用的NSGA-II算法:种群规模为200;初代种群通过随机采样获取;使用模拟二进制交叉算法,交叉概率为90%;使用多项式变异算法,变异概率为10%;终止条件为迭代300次. 优化流程如图3所示.
5 优化结果分析
通过优化计算,获得Pareto最优解集Ω,各目标函数之间的Pareto前沿如图4所示.
从图4可以看出f1与f2、 f3、 f5之间呈正相关,f1与f4呈负相关,可以得出f4与f2、 f3、 f5之间也呈负相关. 呈负相关的目标之间是相互对立的,一个目标值的减小会伴随另一个目标值的增大,优化结果的选取就需要在它们之间进行权衡. 使用权重系数法选取优化结果,方法如下:
式中:wi为目标函数fi的权重系数;xm,为解集中第m个解(m = 1,2,3,…,100);x0为优化前的参数向量. 对于xm,其R(xm)值越小,说明该解相对优化前性能提升越多. 由于f4与其他4个目标均呈负相关,当w4为其他目标的权值之和时,表示刚好均衡了各对立目标,没有选择更偏向于某一性能. 故这里w1-w5的取值分别为1、1、1、4、1,经计算,选取解集中具有最小R(xm)值的解作为优化结果进行对比分析.
在图4中,A点为HIS系统优化后选取的优化结果对应的点,B点为HIS系统优化前目标值点,C点为传统悬架目标值点. 比较A、B、C 3个点所在位置:C点都位于离Pareto前沿较远的位置,说明传统悬架的性能与HIS系统差距较大,HIS系统能够明显的提高车辆的综合性能;在图4(a)(b)(d)中,A点都位于比B点两个目标值都更小的位置,说明对于这些目标函数,A点较B点更优;在图4(c)中,A点刚好位于随一个目标值减小,另一个目标值迅速增大的交界点,说明A点比B点更好的平衡了相互对立的目标.
优化前后HIS系统参数如表5所示,传统悬架与优化前后HIS系统的目标函数值如表6所示. 从表6可以看出,HIS系统比传统悬架的综合性能更好,并且通过多目标优化进一步提升了HIS系统的性能. 比较HIS系统优化前后各目标函数值,f1减少了20.95%,f2减少了12.95%,f3减少了8.05%,f4增加了2.47%,f5减少了11.17%. 可以看出,优化后只有f4的值略大于优化前,其他目标函数的值均获得明显的减小,HIS系统的综合性能获得提升.
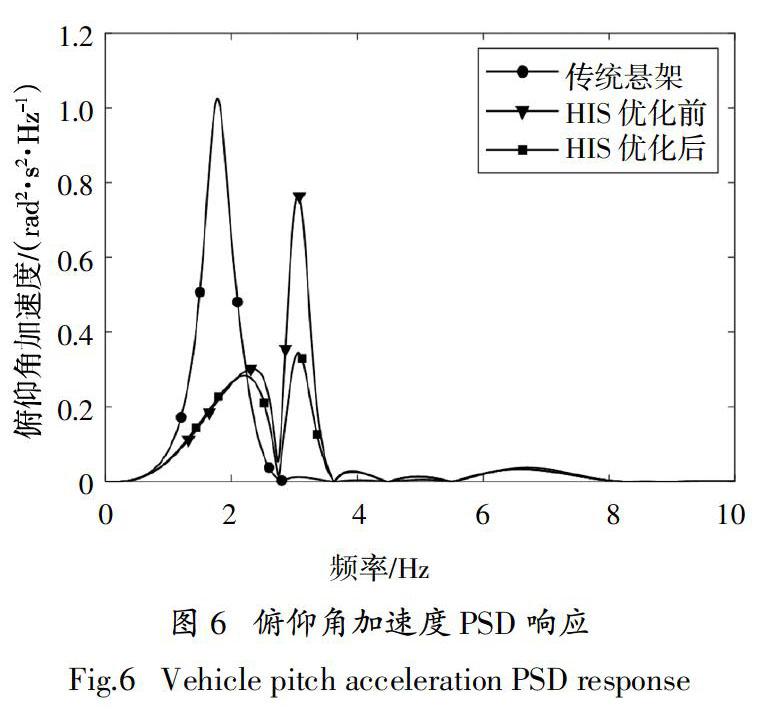
传统悬架与HIS系统优化前后车身垂向加速度、俯仰角加速度、侧倾角加速度PSD响应如图5~图7所示. 对比优化前的HIS系统和传统悬架的各PSD响应:垂向加速度峰值升高;俯仰角加速度峰值降低;側倾角加速度峰值明显降低. 说明未经优化的HIS系统比传统悬架整体性能虽优,但并没有做好各性能的协调. 优化后的HIS系统和优化前进行对比,各PSD响应峰值获得明显降低,其中,车身垂向加速度PSD响应峰值降低了69.38%,俯仰角加速度PSD响应峰值降低了55.08%,侧倾角加速度PSD响应峰值降低了17.02%,优化前后差距明显,效果突出,且均小于传统悬架. 图8为传统悬架与优化前后悬架动行程PSD响应,可以看出:传统悬架的悬架动行程PSD响应幅值几乎在整个频率范围内都大于HIS系统;HIS系统优化后与优化前相比,前后悬架动行程幅值在1.5~2.5 Hz内略有降低,其他频率范围内较优化前略有增大,随着频率增加,与优化前差距越小. 图9为传统悬架与HIS系统优化前后轮胎动载荷PSD响应,可以看出:传统悬架的峰值明显大于HIS系统,在2~7 Hz范围内幅值小于HIS系统;在低频范围内,优化后HIS系统的轮胎动载荷幅值较优化前有所降低,而在高频部分优化前后基本一致. 综上所述,HIS系统的整体性能比传统悬架更优,而通过多目标优化能够使HIS系统获得综合性能的进一步提升,系统各性能之间也更加协调.
6 结 论
通过建立7自由度的“机-液”耦合整车频域动力学模型,对HIS系统参数进行了全局灵敏度分析,并对HIS系统进行了多目标优化,可以得到如下结论:
1)通过HIS系统参数灵敏度分析,定量地分析了HIS系统各参数对其性能的影响程度,结果表明,管路阻尼阀线性损失系数对HIS系统各性能指标都有较大影响;蓄能器阻尼阀线性损失系数对车辆俯仰有一定的影响;系统平均压力对车辆侧倾影响明显;各参数的交互作用对车辆的侧倾有着较大的影响.
2)通过HIS系统的多目标优化,获得Pareto最优解集,通过对使用权重系数法选取的优化结果的对比分析表明:权重系数法能很好的平衡相互对立的目标,选取各性能更均衡的解;优化后的HIS系统除悬架动行程均方根值有略微增大外,其他各目标函数值获得明显降低;除悬架动行程PSD响应幅值略有增大外,其他性能指标的PSD响应峰值获得大幅度的降低. HIS系统比传统悬架具有更优的性能,且优化后HIS系统性能比优化前获得显著提升.
参考文献
[1] ZHANG J,DENG Y,ZHANG N,et al. Vibration performance analysis of a mining vehicle with bounce and pitch tuned hydraulically interconnected suspension[J]. Chinese Journal of Mechanical Engineering,2019,32(1):5.
[2] LI H,LI S,SUN W. Vibration and handling stability analysis of articulated vehicle with hydraulically interconnected suspension[J]. Journal of Vibration and Control,2019,25(13):1899—1913.
[3] SMITH W A,ZHANG N,HU W. Hydraulically interconnected vehicle suspension:handling performance[J]. Vehicle System Dynamics,2011,49(1/2):87—106.
[4] WANG L,ZHANG N,DU H. Experimental investigation of a hydraulically interconnected suspension in vehicle dynamics and stability control[J]. SAE International Journal of Passenger Cars-Mechanical Systems,2012,5(1):759—768.
[5] 丁飞,张农,韩旭. 安装液压互联悬架货车的机械液压多体系统建模及模态分析[J]. 机械工程学报,2012,48(6):116—123.
DING F,ZHANG N,HAN X. Modeling and modal analysis of multi-body truck system fitted with hydraulically interconnected suspension[J]. Journal of Mechanical Engineering,2012,48(6):116—123. (In Chinese)
[6] LIANG J,WU J,ZHANG N,et al. Interval uncertain analysis of active hydraulically interconnected suspension system[J]. Advances in Mechanical Engineering,2016,8(5):1687814016646331.
[7] CHEN S,SHI T,WANG D,et al. Multi-objective optimization of the vehicle ride comfort based on Kriging approximate model and NSGA-II[J]. Journal of Mechanical Science and Technology,2015,29(3):1007—1018.
[8] ZHU H,YANG J,ZHANG Y. Modeling and optimization for pneumatically pitch-interconnected suspensions of a vehicle[J]. Journal of Sound and Vibration,2018,432:290—309.
[9] XU X,YANG M,JIA N,et al. The structure optimization of tracked ambulance nonlinear vibration reduction system[J]. Journal of Mechanical Science and Technology,2017,31(2):523—533.
[10] ZHU X,HUANG J,QUAN L,et al. Comprehensive sensitivity analysis and multiobjective optimization research of permanent magnet flux-intensifying motors[J]. IEEE Transactions on Industrial Electronics,2018,66(4):2613—2627.
[11] PAPAIOANNOU G,KOULOCHERIS D. An approach for minimizing the number of objective functions in the optimization of vehicle suspension systems[J]. Journal of Sound and Vibration,2018,435:149—169.
[12] SMITH W A,ZHANG N. Hydraulically interconnected vehicle suspension:optimization and sensitivity analysis[J]. Proceedings of the Institution of Mechanical Engineers,Part D:Journal of Automobile Engineering,2010,224(11):1335—1355.
[13] SAGLAM F,UNLUSOY Y S. Optimization of ride comfort for a three-axle vehicle equipped with interconnected hydro-pneumatic suspension system[J]. Advances in Automotive Engineering,2018,1(1):1—20.
[14] 周兵,陳逸彬,耿元,等. 互联悬架液压参数灵敏度分析及优化[J]. 中国机械工程,2017,28(19):2269—2274.
ZHOU B,CHEN Y B,GENG Y,et al. Analysis on hydraulic parameters of interconnected suspension based on fuzzy grey correlation[J]. China Mechanical Engineering,2017,28(19):2269—2274. (In Chinese)
[15] 周兵,黄晓婷,耿元. 基于Morris法分析的液压参数对互联悬架的影响[J]. 湖南大学学报(自然科学版),2016,43(2):70—76.
ZHOU B,HUANG X T,GENG Y. Influence of hydraulic parameters on hydraulically interconnected suspension based on Morris[J]. Journal of Hunan University(Natural Sciences),2016,43(2):70—76. (In Chinese)

