紧急避撞工况下的路径规划与跟踪

周兵 万希 吴晓建 陈晓龙 曾凡沂

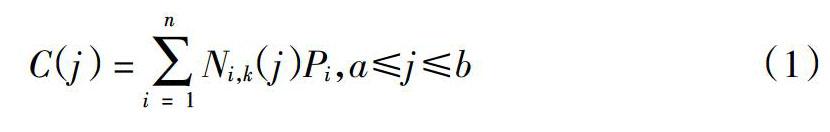
摘   要：高速工况下规划侧向换道紧急避撞路径需考虑避撞与稳定性问题，本文提出了一种基于非均匀B样条曲线、满足多约束要求的路径规划方法. 该方法通过两段非均匀B样条曲线构造出具有曲率连续且加速度呈梯形变化、满足起止点斜率和曲率约束的避撞路径模型，再结合环境信息生成由两个参数控制路径形状的避撞路径簇;在此基础上，构建乘员舒适性目标函数，旨在满足避撞要求的情形下，从路径簇中选取舒适性最优的局部路径;在完成避撞路径规划同时，通过目标函数以及车辆多约束得到优化纵向加速度，完成避撞运动规划;最后采用长于处理多约束控制的模型预测控制算法，通过建立线性时变模型预测控制器控制车辆跟踪规划的路径，验证了路径规划方法的可行性.

關键词：紧急避撞;非均匀B样条曲线;路径规划;多约束;路径跟踪

中图分类号：U463.1                              文献标志码：A

Path Planning and Tracking in Scenario

of Emergency Collision Avoidance

ZHOU Bing1，WAN Xi1?，WU Xiaojian2，CHEN Xiaolong1，ZENG Fanyi1

（1. State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body，Hunan University，Changsha  410082，China;

2. School of Mechanical & Electrical Engineering，Nanchang University，Nanchang 330031，China）

Abstract：To consider the problem of collision avoidance and stability when planning the emergency collision avoidance path of lateral lane under high speed scenarios，a path planning algorithm based on non-uniform B-spline curve is proposed，which meets the requirements of multi-constraint. The proposed collision-free path model constructed by two non-uniform B-spline curves has continuous curvature with trapezoidal change and satisfies the slope and curvature constraint at the starting point and end point; and then，the environmental information is combined to generate a collision-avoidance path cluster whose path shape is controlled by two parameters. On this basis，a passenger comfort objective function is constructed，aiming to select a local path with the best comfort from the path cluster when the collision avoidance requirement is met. Furthermore，the objective function and multi-constrains of the vehicle are used to obtain the optimized longitudinal acceleration so as to complete the collision avoidance motion planning. Finally，the model predictive control （MPC） algorithm specialized in multi-constrained problem is selected to develop a linear time-varying MPC controller，and the feasibility of the proposed path planning method is verified.

Key words：emergency collision avoidance;non-uniform B-spline curve;path planning;multi-constraint;path tracking

统计数据表明，人为驾驶不可避免地存在反应不及时、操控不精确、误操作等局限性，导致90%以上的交通事故与人为因素有关. 智能车辆能够通过高效的环境感知、决策和精准的控制，有效地消除上述局限，提高行驶安全性. 目前，智能车辆相关研究已成为热点.

局部路径规划是智能驾驶的基础和核心技术之一. 根据规划的原理可以将其划分为3大类[1]：基于特定函数的路径规划、基于搜索的路径规划和基于优化的路径规划. 其中，基于特定函数的路径规划是一种采用梯形加速度曲线[2]、多项式[3-5]、B样条曲线[6]等函数计算车辆避撞路径的方法.该方法具有计算高效、曲率变化连续平滑等优点，适用于本文研究的高速避撞这类极端工况. 目前，围绕该方法已开展了大量研究工作. Shim等[4]采用多项式函数建立6次多项式方程，求解得出多项式系数，使路径满足起点和终点约束，但该方法未考虑车辆动力学约束;Gonzalez等[6]采用贝塞尔曲线构造具有曲率连续的避撞路径，通过最大侧向加速度约束得出最大纵向速度，从而实现对纵向速度的规划;孙浩等[7]提出一种基于三次多项式曲线的最优换道轨迹，考虑了乘坐舒适性和安全性，但前提是车辆恒速行驶;陈成等[8]提出了一种由3 个参数确定的四阶贝塞尔曲线来规划路径，并考虑了加速度连续和加速度有界等约束，但忽略了纵侧向加速度耦合约束;金之熔等[9]使用B样条曲线对Dijkstra算法得到的最短路径进行平滑，并考虑时间最优，在规划路径的同时求解速度曲线，最终得到符合车辆动力学特性的最优运动路径;Suzuki等[10]将利用A*算法得到的B样条节点进行平移生成曲率大于最小转弯半径的避障路径，并对控制点位置进行处理，以使车辆尽可能减少转向操作;Wu等[11]使用B样条曲线对人工势场法规划结果进行平滑，实现了减小路径震荡的效果;Choi等[12]在规划双臂机器人路径通过多次删选B样条控制点以达到减少不必要路径抖动的效果;Wan等[13]在B样条曲线控制点连线平行方向增加控制点，使车辆能够通过指定路径点，从而更好地控制车辆可以通过狭窄通道.

学者们在基于特定函数的路径规划方法做了广泛而深入的探索，然而，仍有两个问题需要关注：1） 为了保证生成路径的可行性，通常通过调整函数的参数值生成若干条备选路径，再通过目标函数从中选择. 当确定轨迹函数的参数较多时，生成的备选轨迹会成倍增加，导致筛选耗时;2） 目前，对该类方法的研究主要集中在中低速，且规划轨迹时考虑车辆约束不够全面，如缺少对纵向加速度的约束，以及对纵、侧向加速度耦合的约束等，而这些被忽略的约束在车辆高速避撞控制时往往至关重要.

针对以上问题，本文利用两段非均匀B样条曲线构造出具有曲率连续、满足起（终）点的斜率与曲率约束的避撞路径模型，且其路径兼有梯形加速度曲线的优点，同时路径的形状仅由两个参数确定，减少备选轨迹的生成;而后通过构建乘员舒适性目标函数，添加车辆速度、加速度连续约束，防侧滑约束，纵、侧向加速度耦合约束等多约束，对生成的避撞路径簇进行筛选，最终完成车辆高速避撞路径规划和运动规划.

1   路径规划

1.1   非均匀 B样条曲线的介绍

1.1.1   非均匀B样条曲线的递推式

相较于其它类型的B样条曲线通过控制点和曲线次数改变曲线形状，非均匀B样条曲线形状变化更加灵活，可以通过它的节点矢量加以改变.

k次非均匀B样条曲线定义为：

C（j） = Ni，k（j）Pi，a≤j≤b       （1）

式中：{Pi}（Pi = （Xi，Yi））是决定样条曲线形状的控制点的位置坐标;{Ni，k（j）}是在非周期且非均匀节点矢量χ上的k次样条基函数.

χ = [a，…，a，jk+1，…，jm-k-1，b，…，b]    （2）

式中的节点个数为m+1，非均匀B样条曲线的次数k、控制点数（n+1）、节点数（m+1）之间的关系为：m = n + k + 1.

k次非均匀B样条曲线基函数Ni，k（j）定义为在给定一个非递减的节点矢量χ = [ j0，j1，…，jn]，有：

Ni，0（j）=1，ji ≤j≤ji+1

0，else

Ni，k（j）=

Ni，k-1（j）+

Ni+1，k-1（j）（3）

当式（3）中出现%的形式时，约定其比值为0.

一般地，路径规划采用3次或3次以上的非均匀B样条函数，使生成的路径能够在整个区间具有连续的二阶导数，即具有连续的路径曲率. 需要注意的是，增加样条函数次数可以提高曲线的自由度，但势必增加计算消耗. 考虑到本文研究的高速紧急避撞工况对路径规划的实时性要求较高，在此，将采用3次非均匀B样条进行路径规划.

1.1.2   非均匀B样条曲线控制点的确定

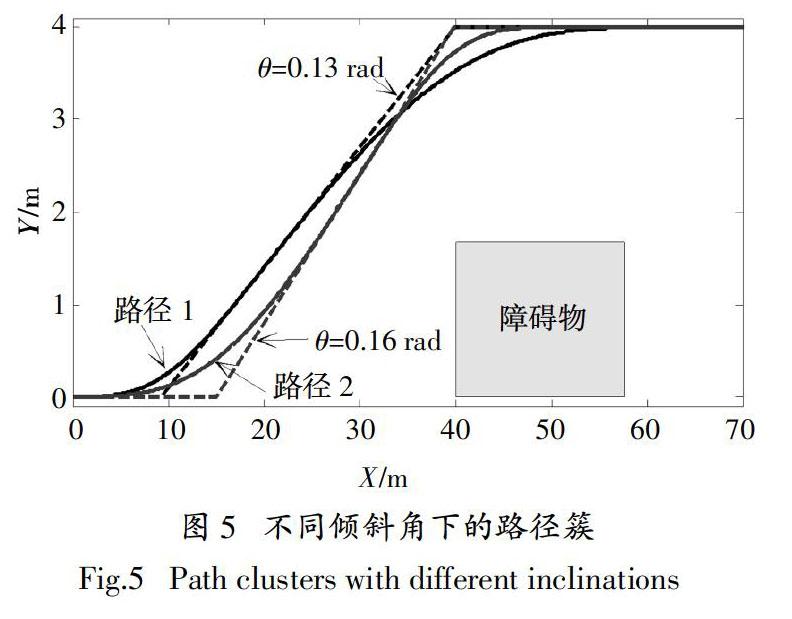
为使路径拥有较好的平滑性，文献[14]提出了一种非均匀B样条曲线控制点确定方法. 本文在该方法基础上，通过融入路径信息，进行路径规划. 具体而言，如图1所示，通过车辆的初始位置（X0，Y0，φ0）和目标位置（Xend，Yend，φend）确定两条相交的直线，构成过渡路径以配置样条曲线的控制点. 为使路径起止点的方向与车辆方向相同，且保证从初始位置到目标位置之间的曲线曲率连续，本文选用6个对称的控制点确定每段B样条曲线，控制点的定位由式（4）确定.

P0 =B+l1 a，P1 =B+

a，P2 =B+

a，

P3 =B+

b，P4 =B+

b，P5 =B+l2 a（4）

式中：B点为两直线的交点;a和b为两直线的单位向量;l1和l2为前、后转弯准备距离，其中，l1为车辆当前位置与交点B的距离，l2为车辆目标点与交点B的距离;τ为控制点的定位参数.

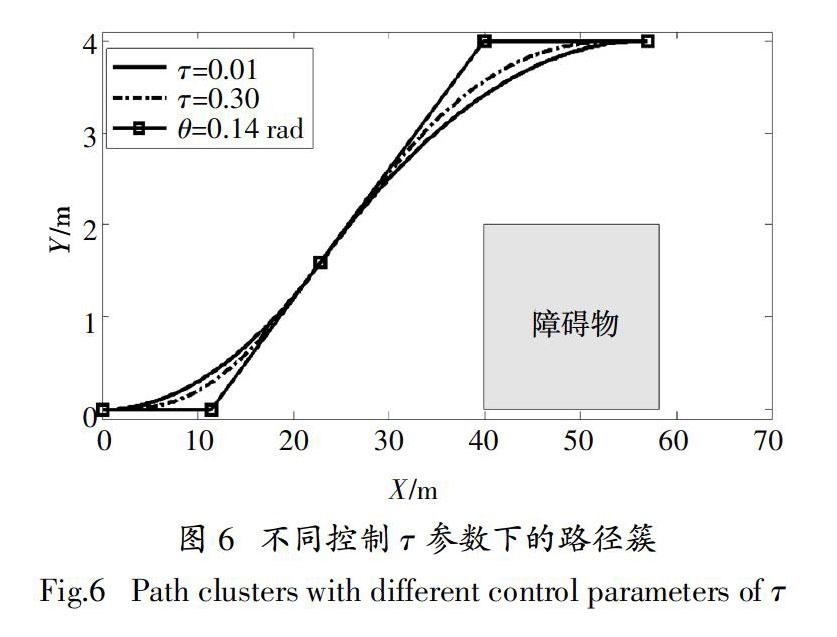
当前、后转弯准备距离确定后，由参数τ确定B样条曲线的控制点及对应的节点矢量χ.

[（X0，Y0，φ0）][（Xend，Yend，φend）][O][Y][X][P4][P3][P1][P2][P5][l2][P0][φ0][l1][φend][B][b][a]

圖1   非均匀B样条曲线控制点的确定

Fig.1   Determination of control points

of non-uniform B-spline curve

车辆的侧向加速度与道路曲率的关系满足ay = v2

xρ，在车辆纵向速度变化不太大的情况下，应尽量使道路曲率的变化与车辆侧向加速度的变化趋势相同. 本文选用的确定B样条曲线控制点的方法能够达到这一目的. 因车辆的加速度常采用梯形加速度模型，本文的B样条曲线控制点，其曲率函数可表达为式（5），如图2所示，根据式（5）得到的曲率变化曲线也呈现梯形.

1.2   局部最优路径规划及速度规划

紧急避撞路径规划的工作原理可概括为图3. 详细而言，为了使整段避撞路径的曲率呈梯形变化，路径采用两段B样条曲线构成. 同时，由于控制B样条曲线的参数是可变的，因此可以生成一组路径簇. 本文在避撞路径簇的基础上，进一步构建乘员舒适性目标函数，旨在满足避撞要求的情形下，选取产生一条舒适性最优的局部路径;与此同时，还将由目标函数得出车辆的最优纵向加速度.

1.2.1   场景信息的提取与紧急避撞路径模型的建立

设车辆行驶于如下工况：车辆当前坐标位置为（0，0，0），车速V0 = 90 km/h，车宽wv = 2 m，静止障碍物位置坐标为（40，0，0），障碍物的宽度wobs = 2 m，车辆与障碍物的期望安全距离Sd = 1 m. 通过上述路径规划方法得出的避撞路径如图8所示.

图9展示了最优、次优路径对应的纵、侧向加速度. 实线为最优路径的纵、侧向加速度，虚线则为次优路径的纵、侧向加速度. 最优路径的侧向加速度变化较快，但最大侧向加速度值小于次优路径的最大侧向加速度值. 同时，最优路径的最大纵向加速度也小于次优路径的最大加速度. 因此，从舒适性角度来说，最优路径的舒适性更好.

隨后，通过最优路径的纵向加速度可得出纵向期望速度，如图10所示. 在该仿真工况中，由于车辆利用转向进行侧向避撞，轮胎的纵向制动力所需不大，故使车辆的纵向速度减小较少. 图中，车辆的纵向速度由初始时刻的90 km/h下降到完成避撞时的83.7 km/h，可以保持较高速度避障通过.

2   路径跟踪

路径规划后需通过路径跟踪完成避撞控制，本文路径跟踪控制的框架如图11所示. 由于高速避撞工况下，车辆的纵向动力学与侧向动力学存在复杂的耦合关系，车辆纵向动态对侧向动态产生影响，需要将车辆纵向控制器中输出的加速度传递到车辆侧向控制器中，得到更加准确的控制效果.

车辆的纵向速度控制器采用PID控制，侧向控制则采用模型预测控制方法. 模型预测控制（model predictive control，MPC）方法是一种滚动优化控制方法，该方法能够系统地处理控制约束问题，非常适合用于车辆的轨迹跟踪控制. 考虑到非线性模型的MPC方法虽然控制效果好，但计算量大，实时性变差[15]，本文采用Falcone等[16]提出的线性时变模型预测控制算法，将车辆模型在工作点进行局部线性化，可降低求解器的求解难度，加快求解器运算速度，同时保证模型的误差.

2.1   二自由度车辆模型

如图10所示，纵向期望速度在避撞过程中变化很小，利用模型预测控制器控制车辆转向避撞时，在一个时长很短的预测时域内，车辆模型可采用纵向速度恒定的非线性二自由度模型，如图12所示.

式中：ξ（t） = [[y] ，φ，[φ] ，Y，X]T为系统的状态量;u（t） = δf为系统的输入量;ξ（t） = [φ，Y]T为系统的输出量;C为系统输出矩阵;φ表示车辆的航向角;[φ] 表示横摆角速度;X、Y表示车辆在惯性坐标系中的位置;δf表示车辆的前轮转角;lf和lr分别表示车辆质心到前、后轴的距离;Ccf和Ccr分别为前、后轮的侧偏刚度;m为车辆的总质量;Iz为车辆横摆转动惯量.

2.2   线性时变模型预测控制

为了保证模型预测控制器能够实时地输出控制信号，需要简化模型预测控制器中使用的非线性车辆模型，降低控制器的求解计算量. 先通过对非线性车辆模型进行离散化，得到非线性离散车辆模型.

再将非线性离散车辆模型在工作点（ξi，ut）处进行线性化处理后，得到线性时变车辆模型[17].

式中：ΔU（t）=[Δu（t|t），Δu（t+1|t），…，Δu（t+Nc-1|t）]T;Np和Nc分别为预测时域和控制时域;Q和R为权重矩阵;ξr为参考轨迹点. 通过优化问题简化后可以重新表达为：

约束： MΔU≤N.

2.3   跟踪效果的仿真与分析

根据1.4节所述工况下规划的避撞路径，采用Simulink-Carsim联合进行路径跟踪仿真控制，车辆初试速度为90 km/h，路面附着系数为0.8，Carsim中的部分车辆参数如表1所示.

图13为在1.4节所述紧急避撞工况下，根据本文提出的方法规划出的期望速度和跟踪速度对比. 图中，虚线为规划的期望速度，实线为车辆跟踪速度. 可以发现：由于在路径规划过程中加入了加速度约束，车辆的期望速度没有出现突变;即使车辆在高速行驶，并且有大的转向时，车辆的速度变化仍能够跟上期望速度的变化.

图14为规划路径与跟踪路径的对比. 总体上，车辆能够准确地跟踪规划的路径，由于控制器使用线性化处理的车辆模型，造成跟踪时出现小的偏差;其中，最大的侧向误差为0.185 m（高速时，此误差能够接受），车辆与障碍物的最小距离为0.353 m（考虑了自车的宽度），能够保证车辆避开障碍物.

规划的车辆侧向加速度与跟踪侧向加速度的对比，如图15所示. 跟踪路径控制时的侧向加速度变化呈梯形加速度模型变化，其值与规划的侧向加速度比较接近，其中，后半段路径由于车辆的跟踪速度稍大于规划速度，造成跟踪的侧向加速度稍大于规划的侧向加速度.

图16和图17为路径跟踪过程中的横摆角速度和质心侧偏角的变化. 整个跟踪过程中，车辆的横摆角速度的绝对值小于16.34 deg/s，且质心侧偏角的绝对值小于1.55°，这表明车辆在路径跟踪过程中能够保持良好的稳定性.

综合以上分析，本文提出的多约束及多目标最优条件下紧急避撞路径规划方法，能够在保证避撞的前提下，尽可能的保证乘员的舒适性;同时，因在构造路径簇和选择最优路径时，充分考虑了车辆的动力学约束，可确保车辆能够良好地跟踪规划路径.

3   结   论

1）提出了一种基于非均匀B样条曲线构造紧急避撞路径的方法，充分利用传感器所得到的环境信息，得到一组少量且准确的避撞路径簇（备选路径）;在此基础上，利用构建的乘员舒适性目标函数和车辆纵、侧向加速度耦合约束等条件，从避撞路径簇中选取产生一条既能保证乘员舒适性又适合车辆高速跟踪的避撞路径.

2）Simulink-Carsim聯合进行路径跟踪控制结果表明：本文在路径规划时将车辆约束融入规划过程，能够确保车辆在高速紧急避撞时也能精确跟踪路径.

参考文献

[1]    江庆坤. 智能汽车避障危险评估和轨迹规划研究[D]. 长春：吉林大学汽车工程学院，2016：5—11.

JIANG Q K. Threat assessment and trajectory planning for intelligent vehicle obstacle avoidance system[D]. Changchun：College of Automotive Engineering，Jilin University，2016：5—11. （In Chinese）

[2]  SOUDBAKHSH D，ESKANDARIAN A，CHICHKA D. Vehicle collision avoidance maneuvers with limited lateral acceleration using optimal trajectory control[J]. Journal of Dynamic Systems Measurement & Control，2013，135（4）：041006.

[3]    YANG J，QU Z，WANG J，et al. Comparison of optimal solutions to real-time path planning for a mobile vehicle[J].IEEE Transactions on Systems，Man and Cybernetics，Part A：Systems and Humans，2010，40（4）：721—731.

[4]    SHIM T，ADIREDDY G，YUAN H. Autonomous vehicle collision avoidance system using path planning and model-predictive-control-based active front steering and wheel torque control[J]. Proceedings of the Institution of Mechanical Engineers，Part D：Journal of Automobile Engineering，2012，226（6）：767—778.

[5]    宋晓琳，周南，黄正瑜，等. 改进RRT在汽车避障局部路径规划中的应用[J]. 湖南大学学报（自然科学版），2017，44（4）：30—37.

SONG X L，ZHOU N，HUANG Z Y，et al. An improved rrt algorithm of local path planning for vehicle collision avoidance[J]. Journal of Hunan University （Natural Sciences），2017，44（4）：30—37. （In Chinese）

[6]  GONZALEZ D，PEREZ J，LATTARULO R，et al. Continuous curvature planning with obstacle avoidance capabilities in urban scenarios[C]//International Conference on Intelligent Transportation Systems. 2014：1430—1435.

[7]    孙浩，邓伟文，张素民，等. 考虑全局最优性的汽车微观动态轨迹规划[J]. 吉林大学学报（工学版），2014，44（4）：918—924.

SUN H，DENG W W，ZHANG S M，et al. Micro vehicle dynamic trajectory plan with global optimality[J]. Journal of Jilin University （Engineering and Technology Edition），2014，44（4）：918—924. （In Chinese）

[8]    陈成，何玉庆，卜春光，等. 基于四阶贝塞尔曲线的无人车可行轨迹规划[J]. 自动化学报，2015，41（3）：486—496.

CHEN C，HE Y Q，BU C G，et al. Feasible trajectory generation for autonomous vehicles based on quartic bezier curve[J].Acta Automatica Sinica，2015，41（3）：486—496. （In Chinese）

[9]    金之熔，申立勇. 基于二次B样条的时间最优轨迹规划[J]. 系统科学与数学，2018，38（12）：1364—1375.

JIN Z R，SHEN L Y. Time optimal trajectory planning based on quadratic B-spline [J]. Journal of Systems Science and Mathematical Sciences，2018，38（12）：1364 —1375. （In Chinese）

[10]  SUZUKI K，USAMI R，MAEKAWA T. Automatic two-lane path generation for autonomous vehicles using quartic B-spline curves[J]. IEEE Transactions on Intelligent Vehicles，2018，3（4）：547—558.

[11]  WU Z，SU W，LI J. Multi-robot path planning based on improved artificial potential field and B-spline curve optimization[C]//2019 Chinese Control Conference （CCC）. Piscataway N J：IEEE，2019：4691—4696.

[12]  CHOI Y，KIM D，HWANG S，et al. Dual-arm robot motion planning for collision avoidance using B-spline curve[J]. International Journal of Precision Engineering and Manufacturing，2017，18（6）：835—843.

[13]  WAN N，XU D，YE H. Improved cubic B-spline curve method for path optimization of manipulator obstacle avoidance[C]//2018 Chinese Automation Congress （CAC）. Piscataway N J：IEEE，2018：1471—1476.

[14]  王振華，章卫国，李广文，等. 基于非均匀B-样条的G2路径平滑方法[J]. 系统工程与电子技术，2011，33（7）：1539—1543.

WANG Z H，ZHANG W G，LI G W，et al. G2 path smoothing using non-uniform B-spline[J]. Systems Engineering and Electronics， 2011，33（7）：1539—1543. （In Chinese）

[15] BORRELLI F，FALCONE P，KEVICZKY T，et al. MPC-based approach to active steering for autonomous vehicle systems[J]. International Journal of Vehicle Autonomous Systems，2005，3（2/4）：265—291.

[16]  FALCONE P，BORRELLI F，ASGARI J，et al. Predictive active steering control for autonomous vehicle systems[J]. IEEE Transactions on Control Systems Technology，2007，15（3）：566—580.

[17]  ABBAS M A. Non-linear model predictive control for autonomous vehicles[D]. Oshawa：University of Ontario Institute of Technology，2011：22—63.