基于多算法结合的机器人路径规划算法
邱浩++杨为民++鲜子霆

摘要: 机器人的路径规划目前已有多种解决方案,如模拟物理学中场概念的人工势场算法,以及智能算法中的遗传算法。但每一种算法都有一定的局限性,每一种算法只在一定条件下才能达到最好的效果。本文着眼于对各个算法适应的条件进行分类,在相应的条件下使用相应的算法,开发出CPP(Combination Path Planning)算法,从而克服的各个算法的缺点,让每种算法的优点得到充分发挥。
关键词:路径规划;条件适应;遗传算法;人工势场算法
中图分类号:TP242 文献标识码:A 文章编号:1009-3044(2016)17-0174-03
Abstract: There are variety of solutions of Robot path planning, such as the algorithm called artificial potential field algorithm, which simulation the potential form physics concept and genetic algorithm. But some limitations with these algorithm, which only gets the best result under certain conditions. So it is necessary for us to use one algorithm under the conditions match it best, by which every algorithm can work more effective.
Key words: path planning; condition match;genetic algorithm; artificial potential algorithm
为了更加深入的学习多智能体系统,开创了RoboCup项目,即机器人世界杯。近几年来,机器人足球的国际赛事越来越普及。RoboCup是其中影响最大的。而路径规划问题又是RoboCup3D项目中的一个热点研究领域。所谓路径规划,就是在仿真环境中找到一条从起点到终点的最优,即最短路径。不仅要考虑到路径长度,还要考虑到障碍物的干扰。这样,路径规划问题就涉及了实时避障问题,这两个问题是反映智能双足机器人的自主能力的关键性问题。如何在各种复杂的环境中找到无碰撞的最优路径本身就是一个高度智能的过程。基于此问题的算法近年来也是层见叠出,新的算法和对传统算法的改进算法不断涌现出来。有以模拟退火算法,人工势场算法和模糊逻辑算法为代表的传统算法;还有图形化的算法,如C空间图形法,自由空间法,以及栅栏法;而最新研究的智能仿生学算法从生物处的得到启示,从蚁群觅食中得到的蚁群算法,从动物神经网络行为中学到的神经网络算法,还有模拟达尔文遗传选择和自然淘汰的遗传算法。以上的每种算法都有其优缺点,栅栏算法在一定的条件下可以得到最优解,但是解的质量取决于栅栏大小的选择,栅栏越小,所需要的储存空间也更大。而可视图法每经过一定周期,就需要重新计算路径,寻找效率较低,以上两种方法求得的路径为折线,不适于机器人的运动控制;人工势场算法虽然克服了上述算法的缺点,但是存在局部最优解的问题,即规划路径非全局最优。而发展火热的智能仿生学算法却因为其需要大量的存储空间以及相当高的时空复杂度而不能在实时避障问题中大显身手,还需要我们不断地研究发展才能应用到实际问题中。既然每种算法都有其适用范围和不适用范围,那我们可以就环境条件进行分类,在每种环境下使用其适用的算法,可以让每种算法的缺点得到最大程度的缩小,而优点得到充分放大。本文就采用能够得到全局最优解的遗传算法和存在局部最优问题的人工势场算法。两种方法结合,在RoboCup3D的仿真平台上测试。3D仿真平台是采用C/S模式设计的机器人足球比赛平台,平台实现对真实的物理三维世界模型的模拟,该系统主要用于研究服务器的通信,基本动作及决策系统,对球员的感知等基本功能模块。
1 遗传算法
1.1遗传算法路径规划的具体方法
遗传算法(Genetic Algorithm,GA)启发于自让进化的模型, 是一种在自然选择和遗传基础上发展来的全局优化算法。编码、适应度函数、初始群体、控制参数和遗传操作过程是遗传算法的五个基本要素;而遗传操作又包括选择、交叉复制、变异。
障碍物的描述:
在综合考虑障碍物的搜索范围和搜索效率等条件的情况下,以机器人的起始点S与目标点D的连线长度|SD|为长,以|SD|/2位宽确定障碍物区域α,则区域α为障碍物搜索范围。用集合Obstacle{}表示障碍物集合,元素为On,如第一个元素为O1,第二个元素为O2。且α内On的表示为On(xn,yn)∈α,其中xn和yn分别为第n个元素在球传平面的横坐标和纵坐标。
将区域α的长分为m+1等分,宽分为n+1等分,这样α内就有了m*n个路径点,在每一条平行于宽线的线(我们暂且称之为横线,m条)上有n个路径点,在每一条横线上取一个路径点,这样便形成了一条由各个横线上的路径点连成的一条路径线β,我们这样表示β:
其中Ln表示从开始点S开始第n条横线上的一个路径点P,xn、yn表示相应的二维坐标。
1.2建立启发函数
启发函数关系到遗传迭代的方向,在最优路径的规划中,我们要考虑到路径长短,距离障碍物距离以及路径平滑度三个因素。
路径长度启发函数为:
[f1=|LiLi+1|] (其中i从1到m-1)
距离障碍物启发函数 :
[f2=DistanceL,Oi](其中i从1到m-1),其中Distance表示障碍物集合中的任一障碍物到路径的垂直距离。
路径平滑度启发函数 ?3=∑∠LPi(其中i从1到m-1),其中∠LPi为第i个路径点所连两条路径的夹角。
综上,得出启发函数为 :
[f=f2+f3-f1]
1.3遗传操作
编码,采用二进制编码表示出路径点,可将每一条横线上的点编号,并用二进制编码,这样每条路径都可以用相应的二进制序列表示出来。
选择合适的初始化参数,确定群体的大小、交叉概率以及最大遗传代数。
随机产生初始种群,即随机产生一条路径。
算出当前种群中各个个体的适应度,并记录最优个体。
通过交叉复制和变异操作产生新的种群,并用新种群替换旧种群,此处要注意防止种群退化现象的出现。
2人工势场算法
人工势场算法最先是由Khatib博士在1986年提出,他采用这种方法来实现机器臂移动的避障规划,而后众多科研工作者对该方法进行了深入的研究,并应用到了机器人路径规划的问题中。
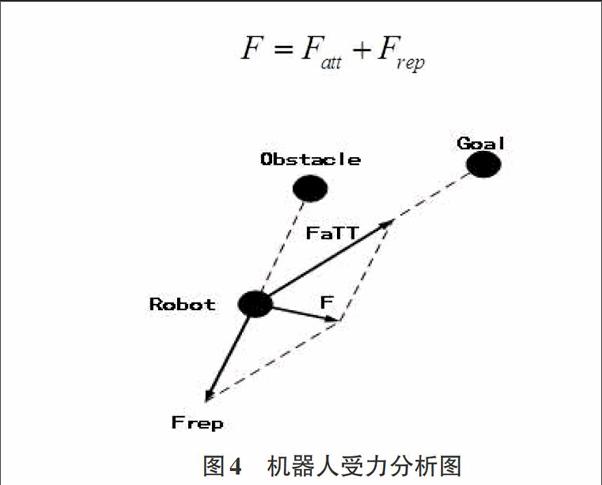
这种算法的基本思想来自于物理上的场的概念,在物理学的电场中,同种电荷之间作用为斥力,异种电荷间作用为引力。类比于这种思想,在机器人的运动空间中建立一个引力和斥力共存的势场,因为目标是要到达目的地D,故在D点加入一个引力场,对机器人起吸引作用,且这个引力场的有效范围是机器人的运动空间;在障碍物点加入一个斥力场,对机器人起排斥作用,应注意的是,该斥力场的作用范围并不是机器人的全部运功空间,而是以障碍物所在点为圆心,以一定距离为半径的圆。机器人在自起始点向目标点运动的过程中,全程受到目标点的引力作用,每当进入障碍物斥力作用范围,便会受到斥力作用而偏离障碍物。图3是人工势场算法模型图。
在其他介绍人工势场算法的文献中,都将势函数与距离关联起来,即势函数是关于距离的函数。下面给出一种势函数形式,作为介绍。
机器人受力分析图如图4。
3结合路径规划算法
上面介绍了遗传算法和人工势场算法的基本方法。在遗传算法,m和n的取值直接影响到遗传结果的优劣,当m和n取较大时,搜索区域α分的足够精细,会取得较好的路径结果,但算法的时空复杂度会很高,无法达实时避障的要求;反之,若取值较小,虽然计算速度会得到提升,但计算的结果却不尽如人意。再来看看人工势场算法,该算法是一个传统算法,能够很好地实现实时避障,但该算法有局部性问题,常常会陷入局部最优的路径中,很难计算出全局最优的路径。
作者尝试一种新的思路,对环境条件进行分析,根据环境来选择不同的路径规划算法,可以最大程度的发挥各算法的优势。如何判断环境条件,成了问题了的关键。人工势场算法具有很好的实时性,在时间相对较为急迫,或者说,从开始点到目标点的直线距离较近时,人工势场算法更加适合。作为尝试,作者在这里只选取了遗传算法和人工势场算法,读者可以自行尝试加入其他算法。
我们设置两个环境条件参数,这两个参数将帮助我们在相应的环境下合理地选择路径规划算法。
Dis:起始点到出发点的直线距离;
OB_N:在搜索区域α中,每单位面积中障碍物的个数。
其中,Dis的值我们可以直接根据S点和D点的二维空间坐标直接得出,而求OB_N需要知道搜索空间α中障碍物的总数以及搜索空间α的面积。搜索空间α的面积为Dis与Dis/2的乘积,即Dis2/2;搜索空间中障碍物的总数可以通过穷举障碍物集合中的所有元素,并一一判断是否在搜索空间中得出。在3D平台中,对方球员和我方球员均为障碍物,故除去自身,最多有21个障碍物。
在计算出这两个参数的值以后,便可以使用这两个参数来参考决定应该使用的路径规划算法。在Dis大于一定值得情况下,我们需要取得偏向全局最优的结果,应使用遗传算法进行计算;在Dis小于一定值得情况下,时间较为紧迫,应当采用实时性较强的避障算法,故采用人工势场算法;当Dis在一定区间时,参考OB_N的值,OB_N较大,搜索区间较为拥挤,采用人工势场算法;反之OB_N较小,采用遗传算法。算法选择图如图5。
其中的a,b,c人为确定,可以多次试验以取得较优值。
4实验结果
4.1实验平台与环境
本实验在RoboCup3D平台下进行,系统为Ubuntu14.04,rcssserver3d版本0.6.9,Roboviz可视化监视器。
4.2实验结果
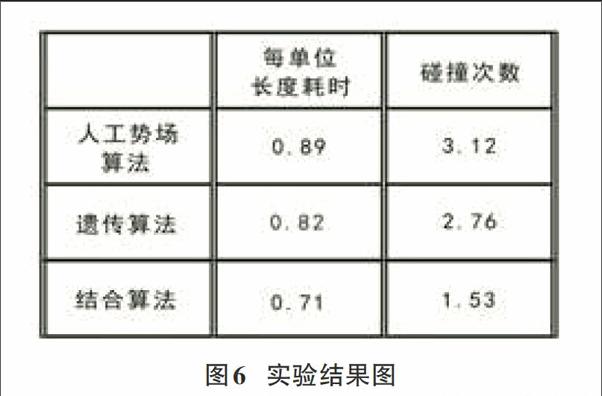
设定多组参数(a,b,c),经实验分析后选择较优组合,其中a为12;b为20;c为10/128。将结合算法与遗传算法和人工势场算法分别应用在Dreamwing3D队伍代码中,并进行多次实时对抗,观察到避障效果明显优化,同时记录相应数据,如图6所示。
经实验得出,基于遗传算法和人工势场算法的结合路径规划算法,路径规划效果明显优于单独应用上述两种算法之一。
参考文献:
[1] 吴晨光.基于改进人工势场法的机器人路劲规划及其在RoboCup中的应[D].南京:南京邮电大学,2012:16-20.
[2] 宿鲁艳,梁志伟.RoboCup3D仿真平台中足球机器人的避障规划[D].南京:南京邮电大学,2013:1-5.
[3] 樊明涛,杨宜民.基于遗传算法的双足足球机器人路径规划[J]. 现代计算机:专业版,2012(36).
[4] 郑重虎.RoboCup3D仿真中双足机器研究与开发[D].南京:南京邮电大学,2012:1-5.
[5] 人的运动规划与智能决策[D].南京:南京邮电大学,2013:8-19.
[6] 肖南峰.智能机器人[M].广州:华南理工大学出版社,2008.
[7] 蔡自兴.机器人学[M].北京:清华大学出版社,2009.
[8] 吴青松.基于遗传算法的移动机器人路径规划研究[D].西安:电子科技大学图书馆,2005.
[9] 王于,林良明,颜国正.动态避障物环境下移动机器人路径规划[J].上海交通大学学报,2002,10(10):1430-1434.
[10] 李智也.移动机器人路径规划问题的解决方案[J].计算机工程,2006,32(1):189-192.

