变负荷工况下往复压缩机活塞杆运行轴心轨迹特征提取

周 超 ，张进杰 ，张旭东 ，孙 旭 ，王 瑶 ，2

（1.高端机械装备健康监控与自愈化北京市重点实验室，北京化工大学，北京 100029；2.压缩机技术国家重点实验室（压缩机技术安徽省实验室），合肥 230031）

0 引言

由于生产工艺与需求波动导致往复压缩机运行负荷改变是石油、炼化企业的常态。运行负荷的改变，如进排气压力改变、顶开进气阀回流等都将导致压缩机缸内工作状态变化，进一步影响活塞杆、连杆、曲轴等运动部件受力与运行。根据企业调研，安装无级气量调节系统的往复压缩机发生连杆、十字头、活塞杆部件故障的比例较高［1］。

变负荷工况下故障监测诊断一直是难点问题［2-4］。负荷变化通常导致机械结构动态特性改变，使振动、位移等信号中的故障特征受到干扰。活塞杆是往复压缩机核心运动部件，易发生紧固元件松动、裂纹甚至断裂故障。针对往复压缩机故障监测诊断的研究报道已经较多，也有开展活塞杆轴心轨迹的研究报道。马波等［5］利用声发射技术对活塞杆进行在线监测，以声发射幅度作为监测参数，实现了事故的早期预警；马晋等［6］提出一种基于X方向、Y方向的活塞杆轴心位置轨迹的故障诊断分析方法，该方法可实现往复压缩机活塞组件、活塞杆的潜在故障早期预警；Jiang等［7］针对活塞杆轴心轨迹杂乱、提取特征困难的特点，基于谐波小波完成活塞杆轴心轨迹提纯处理，提取振动能量、固有频率与轨迹包络面积等特征，利用非线性局部切空间流行学习算法对特征进行降维获取敏感特征，用于监测诊断，证明了该方法对往复压缩机活塞杆故障监测的有效性；王庆锋等［8］提取活塞杆轴心振动能量、轴心轨迹面积及单一方向振动能量参数，能有效反映活塞杆运行状态，相对位移平均值受安装因素影响较大，该方法对故障监测效果较好，特别对断裂、撞缸故障更加敏感。

但是针对变负荷工况下活塞杆运动特征提取的研究少有报道。当工况改变与故障同时发生时，活塞杆运行状态改变的根本原因需要明确，应针对负荷影响与故障影响分别进行特征挖掘，避免故障误判。因此，变负荷状态下的活塞杆瞬态运动特性研究必要性强。

本文提出一种基于活塞杆轴心轨迹离散点分布轮廓包络与信息熵的特征提取方法，挖掘不同负荷工况下的活塞杆轴心轨迹特征，进一步采用流形学习方法进行特征降维后，构建负荷敏感特征集，利用神经网络构建负荷识别模型，实现压缩机运行负荷的自动识别。相关研究成果和应用常规凸集包络等方法提取特征进行对比，验证本文方法的有效性。

1 活塞杆轴心位置轮廓与信息熵特征提取

1.1 活塞杆轴心轨迹提取［9］

往复压缩机在线监测系统通常使用电涡流传感器监测活塞杆位移信号，包括竖直方向的沉降量和水平方向的偏摆量。以竖直方向沉降量计算为例，令传感器初始安装时探头距离活塞杆距离为L0，传感器采集的电压为V0，则：

式中K——传感器灵敏度；

B——传感器初始偏置量。

某一时刻，传感器采集的电压为V1，则：

式中L1——当前时刻探头距离活塞杆的距离。

在线监测系统中，活塞杆沉降量RY的计算式为：

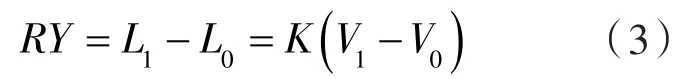
水平方向偏摆量计算方法与上式类似。进一步利用如图1所示的位置关系，借助沉降与偏摆量监测计算活塞杆轴心位置。

图1 活塞杆轴心位置示意

初始时刻，活塞杆轴心的坐标为O0（0，0）。运行一段时间后，活塞杆位置出现变动，如图中虚线圆圈表示，此时活塞杆轴心的坐标为O1（x，y）。令活塞杆半径为R，图中RX，RY分别代表水平与竖直传感器采集到的活塞杆位置相对变化量。因电涡流传感器采集电压信号为负，可知当活塞杆距离传感器距离变远时，RX与RY为负，反之为正。由图1可知：

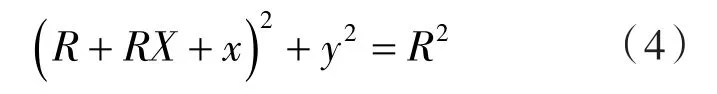
同理可得：

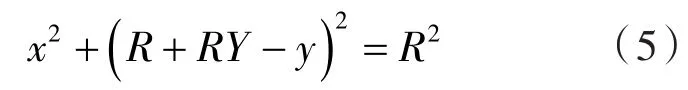
令A=R+RX，B=R+RY将公式（4）、（5）联立，得：

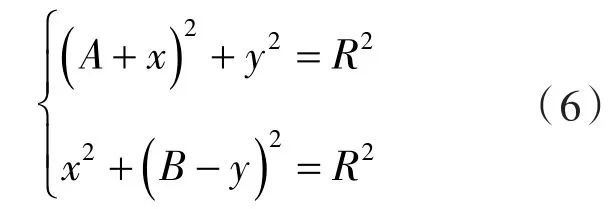
求得x，y存在两组解，根据活塞杆实体结构可排除一组无效解，从而获得活塞杆轴心位置解。

1.2 改进的轴心轨迹离散点轮廓包络

一组典型的活塞杆沉降与偏摆波形数据如图2所示。根据活塞杆结构，由式（6）计算获得活塞杆轴心位置点分布如图3所示。

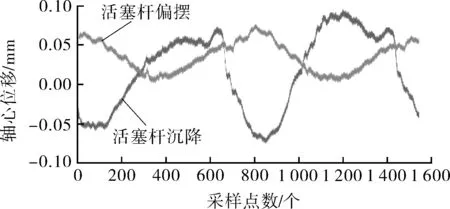
图2 活塞杆沉降与偏摆波形数据

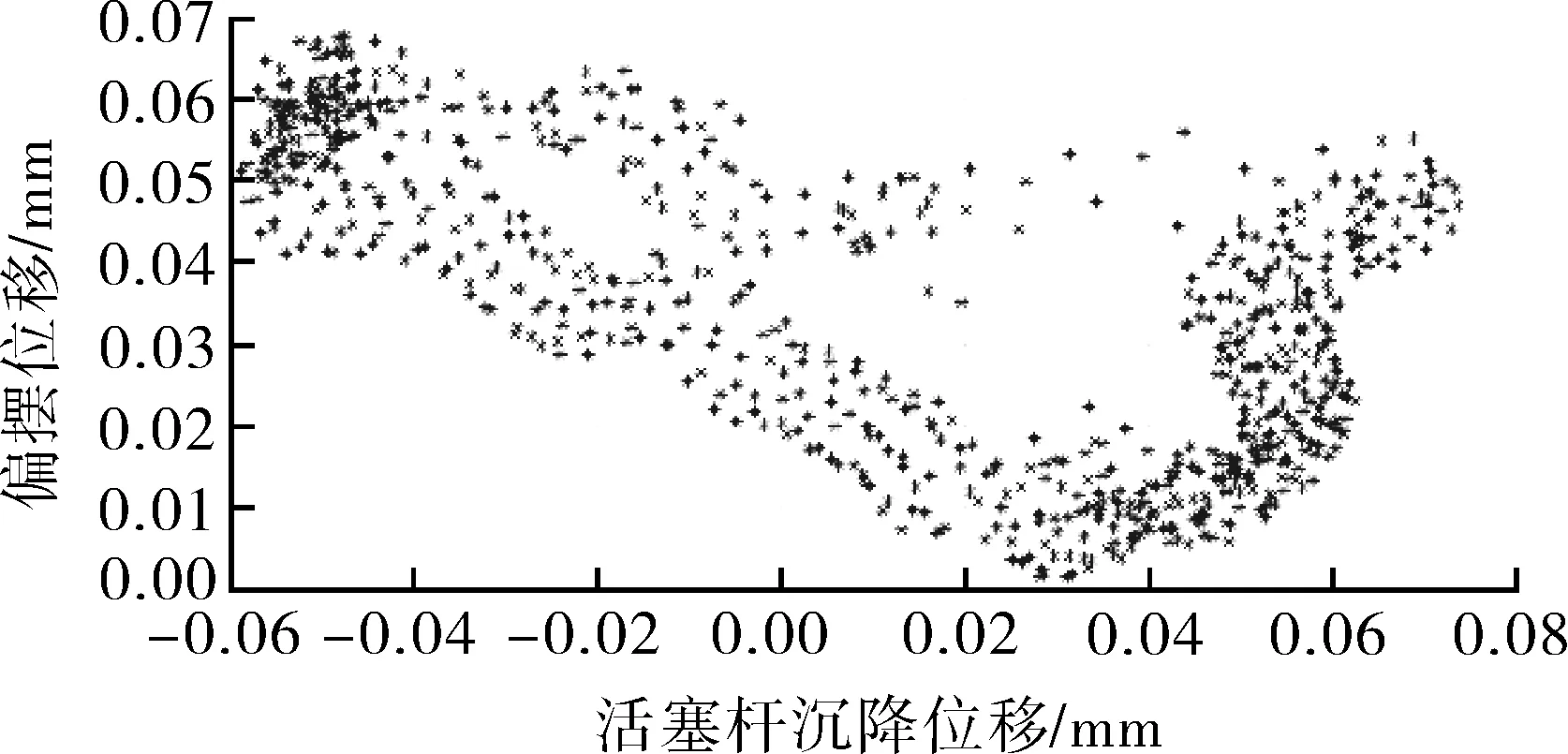
图3 活塞杆轴心位置点分布

已有针对离散点提取轮廓包络的研究报道［9-10］。何小高等［11］提出了一种改进的阶次包络分析方法，用于齿轮箱轴承故障的诊断；黄传金等［12］提出了一种基于全矢谱和复局部均值分解融合的二元全矢包络技术—CLMD全矢包络技术；李泽滔等［13］提出了一种用于故障隔离的参数区间包络线计算方法。本文针对活塞杆轴心位置分布随机性和轮廓具有显著凹凸特性，在现有研究成果基础上提出了一种轴心位置轮廓包络提取方法：

（1）提取轴心位置在X和Y坐标上的4个极限点，分别是X轴最大与最小点和Y轴最大与最小点；特殊情况下，4个极限点存在重合，变为3个极限点。

（2）分别以上述极限点为起点，以逆时针方向，遍历轴心位置点，以斜率最小原则，提取轴心位置轮廓凸集包络。

计算方法如下：

①连接Ymin点与Xmax点，形成线段Ymin-Xmax记斜率为α1。

②遍历线段右侧的点，找出与Ymin点相连斜率最小，且距离最大的点Px。

③以点Px代替Ymin，连接Px与Xmax点，继续遍历线段右侧的点，找出与Px点相连斜率最小，且距离最大的点作为Px点。

④重复上述计算过程，直到Px点与Xmax点重合，其他极限点之间凸集点计算过程与上述过程一致。

⑤计算轴心位置轮廓凸集包络形成的面积S1。

（3）以上述凸集包络，由第一步选择的极限点为起始点，以逆时针方向，逐个对连续2个包络点Pm-Pn进行如下计算：

①连接连续的两点，形成线段Pm-Pn，记斜率为αmn。

②遍历线段左侧的点，找出与Pm点相连斜率最小，且距离最小的点Po。

③以点Po代替Pn，连接Pm点与Po，继续遍历线段左侧的点，找出与Pm点相连斜率最小，且距离最小的点并替代Po。

④重复上述计算过程，直到Po点与Pm点之间的距离不超过L，其他极限点之间轮廓包络点计算过程与上述过程一致。

⑤距离L初始设置为所有轴心位置离散点的平均距离。计算轴心位置轮廓上述包络形成的面积S2。

（4）经过步骤（3）获得一组轴心位置离散点轮廓包络，当S2与S1差值小于5%时，终止计算；当S2与S1差值大于5%时，距离L缩小50%，重复步骤（3），并以S2取代S1，作为下次面积计算的基准。

（5）经过上述计算过程，获得活塞杆轴心位置轨迹外轮廓包络。

1.3 信息熵特征提取方法

轴心位置轮廓包络反映了轴心位置分布的形状特征，为了进一步提取轴心位置分布的聚集特征，采用信息熵方法对轴心位置数据进行处理。

信息熵最早由信息论专家C.E.Shannon运用概率论和数理统计学的方法提出，对事物的不确定性给出了一个科学的计量方法，具有对称性、扩展性、连续性等性质。假设信源由离散随机变量X={x1，x2，L，xn}给定，X的概率分布向量表示为pi=p（x）（i=1，2，L，n），同时，Shannon 定义信息的数学期望为信息熵，则信源信号的信息熵为：

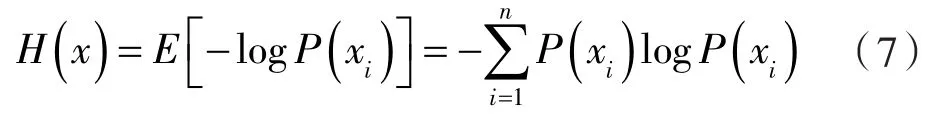
2 活塞杆轴心轨迹特征选择

针对一组典型的活塞杆轴心位置信号进行轮廓包络提取，并与常规的凸集包络进行比较，如图4～6所示。

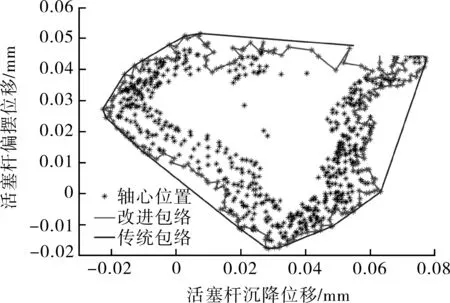
图4 压缩机100%负荷时轴心位置包络

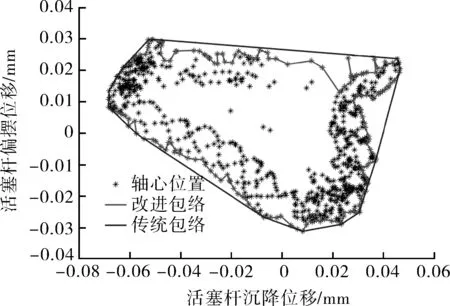
图5 压缩机70%负荷时轴心位置包络

图6 压缩机20%负荷时轴心位置包络

经上述对比可发现：

（1）活塞杆轴心位置分布伴随负荷的变化不断改变，相近的负荷状态下，轴心位置形状较为接近。

（2）本文采用的轮廓包络方法能够较好的反映轴心位置外轮廓形状，对轮廓的凹凸特性形成了较好的包络效果。

将上述包络数据进一步融合信息熵提取结果，分别计算出轴心轨迹的包络特征Xb和信息熵特征Xs，并将2种特征融合为特征集X={Xb，Xs}。采用流形学习方法，进行特征选择，将特征集X={Xb，Xs}进行降维处理，最后将得到的负荷敏感特征集X'={x1，x2，L，xi}，i=1，2，3，L，输入径向基神经网络训练分类模型。

3 试验数据分析与讨论

3.1 试验台设备

本文研究对象为一台2D型空压机。该机组工作参数见表1。在该机组上安装有在线监测系统，监测活塞杆沉降与偏摆信号，同时，机组配备了无级气量调节系统，可实现工作负荷的灵活调节。

表1 试验台往复压缩机工作参数

3.2 数据分析

选取了0%，20%，50%，60%，70%，80%，90%，100% 8种负荷状态下的数据，每种负荷状态下各采集了500组活塞杆沉降与偏摆数据进行分析，采用本文的特征提取方法，形成特征参数集。为验证文中所提方法的有效性，与传统包络方法进行比较，并且对比了有无信息熵特征对最终负荷识别结果的影响。

3.3 对比分析

（1）改进包络方法与传统包络方法。

用2种包络方法分别对数据进行处理，提取包络特征，形成包络特征集，输入流形学习进行特征降维处理后结果如图7，8所示，结果表明，改进包络方法可以得到更优于传统方法的分类结果。

图7 改进包络方法流形学习降维结果

图8 传统包络方法流形学习降维结果

从构建的负荷敏感特征集中随机选取400组X'作为训练数据，100组X'作为测试数据，训练出径向基神经网络负荷识别模型，结果如表2。

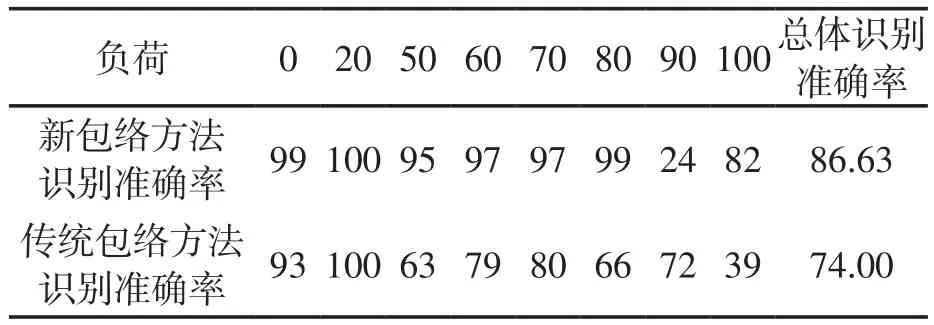
表2 径向基神经网络识别准确率 （%）

结果表明，与传统包络方法相比，文中所提包络方法能够更好的表征不同负荷状态下活塞杆轴心轨迹的特征，从而达到较好的负荷识别结果。

（2）信息熵对分类结果的影响。

将特征集X={Xb，Xs}输入流形学习进行降维，处理结果如图9所示。

图9 增加信息熵特征后的流形学习降维结果

同上述特征分配原则，训练径向基神经网络模型，结果见表3。结果表明，将信息熵特征与新包络特征融合后，负荷的识别准确率得到了提高。

表3 增加信息熵特征后的径向基神经网络识别准确率 （%）

4 结论

（1）提出的包络特征提取方法较之传统包络方法在负荷分类方面具有更加优异的效果，最终的识别准确率高于传统方法10%以上。

（2）与单独包络特征相比，融合信息熵得到的特征集能够更好的表征不同负荷下活塞杆轴心轨迹的特征，并且使识别准确率得到进一步提高。

本文研究成果同时为下一步变负荷状态下往复压缩机故障监测诊断方法研究奠定了基础。