基于二叉树支持向量机的往复压缩机气阀故障诊断方法
肖 军,舒 悦,谢传东,刘晓明,刘志龙
(1.合肥通用机械研究院有限公司 压缩机技术国家重点实验室,合肥 230031;2.合肥通用环境控制技术有限责任公司,合肥 230031)
0 引言
往复压缩机是石油、化工等部门广泛应用的重要动力设备,而气阀是往复压缩机中最为重要的部件,也是最易损坏的部件之一,在所有故障类型中气阀故障占比达36%[1]。因此,开展往复压缩机气阀故障的诊断方法研究十分必要。王朝晖等[2]应用模糊聚类方法从实测故障数据中获取故障特征,对往复压缩机的气阀故障进行诊断,聚类结果与实际情况吻合较好。张思阳等[3]通过对正常、阀片缺口、弹簧失效的实测信号进行经验模态分解、重构和样本熵分析,精确提取故障信息,实现了气阀缺口和阀少弹簧的故障诊断。马晋等[4]采用基于混沌分形理论的方法对往复压缩机气阀的冲击变化信号进行特征提取,把关联维数作为特征参数,实现了气阀故障状态的实时诊断。Ahmed等[5]采用主成分分析法从往复压缩机的14个振动信号特征量中提取有效诊断特征,并通过对Q统计值贡献的研究发现了两个特征量,这两个量的组合可以实现对包括吸气阀故障在内的多种故障模式准确分类。然而,气阀部件的振动信号十分复杂,常规的故障诊断多采用对振动信号进行各种特征提取的方法识别故障状态,能够准确识别的故障类型有限。
支持向量机[6]作为一种基于统计学习理论的机器学习方法,在解决小样本、非线性的问题上具有独特的优势,经过多年的完善和发展已经在振动故障诊断领域获得了一定的应用。然而,传统的支持向量机方法无法解决多故障模式分类的问题。郭创新等[7]提出一种基于多分类多核学习的支持向量机模型,并将其应用于变压器故障诊断,计算实例表明该模型具有较高的诊断准确率。杨珮鑫等[8]针对分布式发电并网保护的功能需求,采用“一对一”方法建立多分类支持向量机,实现了对扰动、孤岛和故障事件的检测。然而基于“一对一”或“一对多”[9]的多分类向量机存在不可分区域,相比之下,二叉树支持向量机具有测试速度快、不存在不可分区域的优点。二叉树支持向量机的分类能力依赖于二叉树结构的生成原理。Govada等[10]实现了一种基于K均值聚类的二叉树结构支持向量机算法,结果表明,该算法具有与“一对一”方法相近的准确度,与“一对多”方法相比,在降低训练和测试时间的同时准确度更高。Qin等[11]对各类样本构造最小包围超椭球,根据超椭球体积生成最优二叉树,并采用Statlog数据库训练多分类向量机,数值试验结果表明,该算法具有较高的分类精度和分类速度。
本文使用小波包分析方法提取往复压缩机气阀振动数据的特征量,运用模糊C均值聚类(FuzzyC-Means Clustering)技术构建二叉树结构,结合支持向量机(Support Vector Machine)方法,构建了基于二叉树支持向量机的多分类器(FCM-SVM),对往复压缩机气阀的故障类型进行准确诊断。
1 算法描述
1.1 模糊C均值聚类
模糊C均值聚类算法由Dunn[12]和 Bezdek[13]提出,其基本思想是使被划分到同一聚类的对象之间相似度最大,根据隶属度确定每个数据点属于某个聚类的程度。设xi(i=1,2,…,n)是N个样本组成的集合,M为聚类中心的数目,定义聚类损失函数。
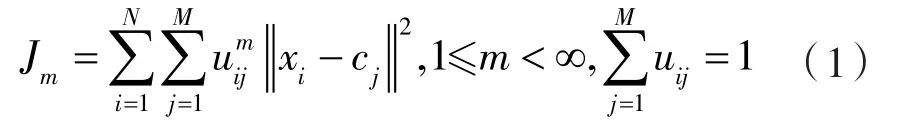
式中m——加权指数;
uij——第i个样本对第j类的隶属度;
cj——第j个聚类中心。
通过以下迭代,使目标函数Jm达到最优。
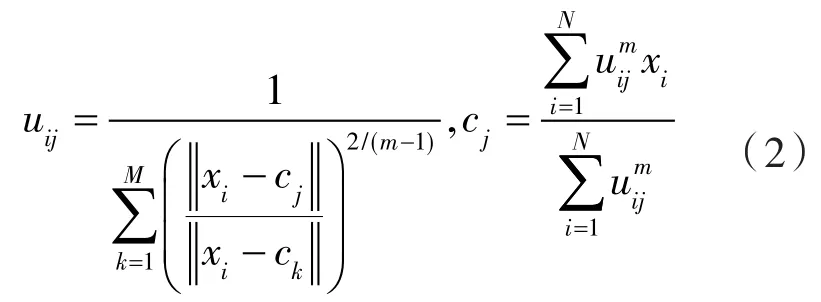
当迭代收敛时,即得到各聚类中心及各数据点对各类的隶属度,根据隶属度值将样本归类。
1.2 支持向量分类机
应用支持向量机方法解决数据集 {(xi,yi)|i=1,2,…,l}的非线性分类问题,可使用非线性映射将输入样本映射至高维特征空间,通过寻找最优分类超平面来实现数据分类。分类超平面的优化问题可表述为:

式中w——权向量;
b——偏置;
ξi——松弛量;
C——惩罚参数;
φ——非线性映射函数。
引入Lanrange乘子αi和βi,与上述条件极值相应的Lanrange函数为:

分别对w,b和ξi求偏导并令其等于零,得到上述优化问题的对偶问题:
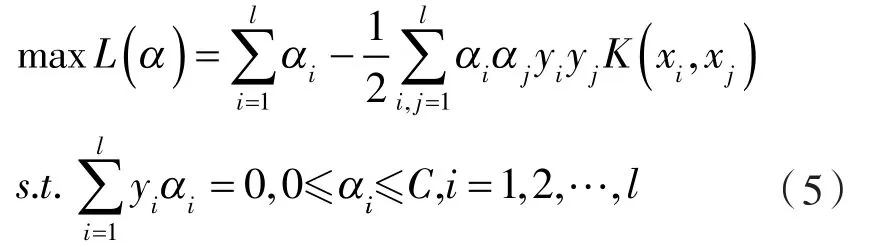
相应的分类决策函数为:
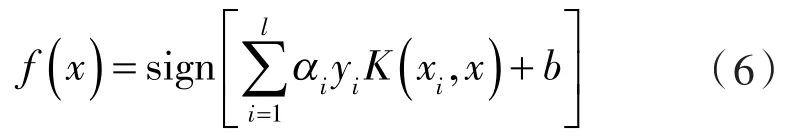
其中K(xi,xj)=φT(xi)φ(xj) 为核函数。αi>0对应的数据点称为支持向量,通常支持向量的数目远小于样本数。不同的核函数构建不同的分类器,目前最常用的是径向基核函数(RBF):
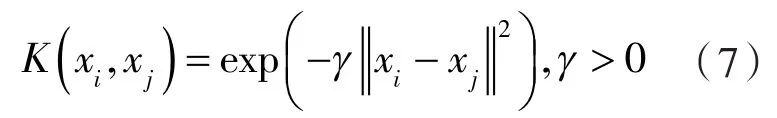
采用序列最小优化算法求解对偶问题(5),具体算法参考文献[14],其空间复杂度与训练样本集大小呈线性关系,能够有效实现支持向量机大样本学习的问题。
1.3 二叉树支持向量机
结合模糊聚类分析和支持向量机的多分类方法可分为知识学习和故障识别两个阶段。在知识学习阶段,采用模糊C均值聚类法构建故障诊断完全二叉树,其基本思想是:运用模糊C均值聚类求出每类故障样本的聚类中心,再对各聚类中心构造一棵二叉树,在二叉树的各个节点,根据聚类中心对应的训练样本构造学习集,训练各个节点的支持向量机子分类器,得到基于完全二叉树的多分类模型,该二叉树结构如图1所示。

图1 基于二叉树支持向量机的多分类模型
具体步骤如下:
(1)对于具有N个样本M个类别的样本集S,根据初始隶属度,利用模糊C均值聚类方法求出每个子集的聚类中心C={c1,c2,…,cM}。
(2)利用模糊C均值聚类法将C聚类为CP和CN两类。
(3)正类样本集P1,由属于CP的各聚类中心对应的训练样本组成,负类样本集N1由属于CN的各聚类中心对应的训练样本组成,训练生成支持向量机SVM1,形成二叉树的根节点。
(4)将CP聚为两类,正类样本P2和负类样本N2由各聚类中心对应的训练样本组成;同理,将CN聚为两类,正类样本P3和负类样本N3由各聚类中心对应的训练样本组成。
(5)由正类P2和负类N2训练生成支持向量机SVM2,由正类P3和负类N3训练生成支持向量机SVM3。
(6)重复步骤(4)和(5),直至构造第M-1个支持向量机SVMM-1。
(7)由步骤(1)~(6)得到M-1个支持向量机SVM1,…,SVMM-1,生成二叉树的中间节点。
2 UCI数据分类试验
为验证本文提出的二叉树多分类器的准确可靠性,首先在UCI机器学习数据库[15]中选用了5组常用于算法性能对比的数据集进行验证试验见表1,这几组数据兼具了特征维度高和维度低的情况,对分类性能的评价更为客观。每组数据集都被划分为2部分,取其中2/3作为训练样本,其余作为准确性验证的测试样本,重复多次划分取计算的平均正确率。采用本文设计的算法(FCM-SVM)与各文献采用的算法进行对比,结果见表2。
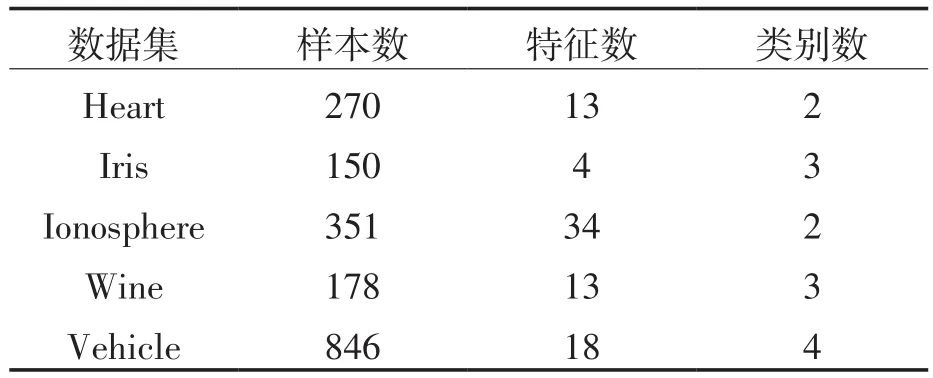
表1 选择的UCI数据集
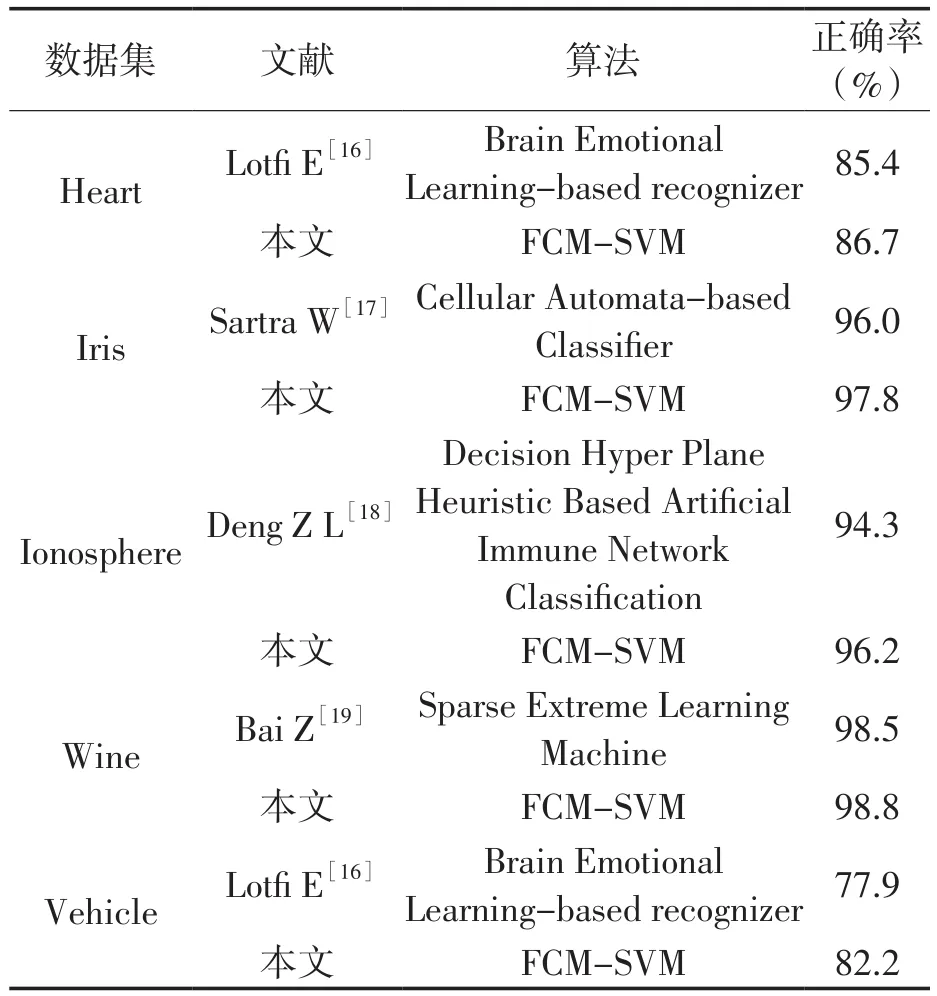
表2 本文算法与其他文献方法的分类正确率对比
由表2可知,本文算法对5组数据集的分类,其正确率均优于其他文献中的计算结果,特别是对于34维的Ionosphere数据集,本文算法的正确率高出近2%,而对于大样本的Vehicle数据集,正确率高出4.3%。通过UCI数据集分类试验,表明了本文算法用于数据分类的准确性。
3 往复压缩机气阀故障诊断
为采集不同状态下的往复压缩机振动试验数据,在往复压缩机故障诊断试验台上安装了正常状态及4种故障状态的气阀阀片进行故障模拟试验,阀片的4种故障状态分别为内环锯断、内环两瓣、内环中环两瓣及三环两瓣。加速度传感器布置在气阀的阀盖上,采样频率为20 kHz,针对不同故障工况选取一个完整采样周期0.1 s的振动信号绘制时域波形,图2示出内环两瓣故障和正常工况采集的振动信号。对于往复压缩机缸体,气阀阀片撞击阀座和升程限制器时产生的冲击脉冲是一个重要的激振源,如果气阀发生故障,冲击激励的变化必然引起阀盖振动特性的变化。由图可见,气阀故障发生时的振动幅值要小于正常工况,但时域振动信号并不能很直观地反映故障特征,如何区分各类故障还需要对振动信号做进一步分析。

图2 吸气阀振动信号
往复压缩机气阀的振动信号具有非平稳性和冲击性,在特征提取过程中应尽可能将信号的频率成分进行细分。小波包分析[20]能够有效划分信号频带,并进行不同频带的能量谱分析,在保持小波分析优良特性的基础上实现了对信号高频部分更加细致的刻画。本文利用小波包方法对气阀振动信号进行分解,在不同频带下重构得到信号的各频带波形,提取信号各频带的能量作为特征量。图3示出阀片内环两瓣故障时,一个采样周期其振动信号经3层小波包分解后8个频带的重构信号,小波类型采用dmey。由图可见,除缸内气流脉动引起的低频信号外,由阀片撞击阀座和升程限制器引起的高频信号能量亦非常显著。
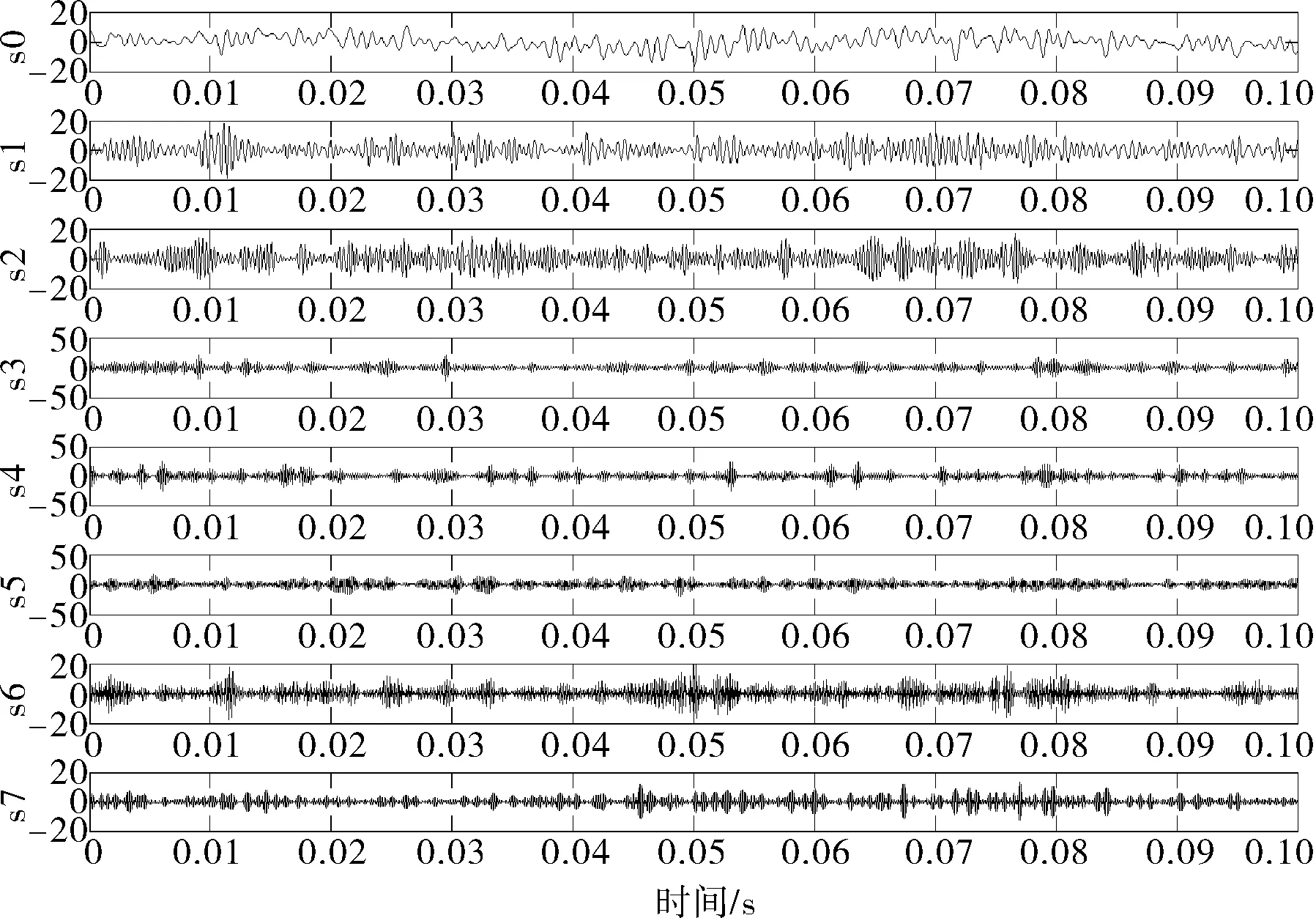
图3 阀片内环两瓣时各频带重构信号
采集阀片在4类故障状态和1类正常状态下的振动信号,对每组信号提取小波包分解后8个频带范围的信号能量作为特征量,构成气阀故障诊断的高维样本数据。每种状态选取40组样本数据共200组样本数据构成训练集,另选取每种状态20组样本数据共100组样本数据构成测试集,训练样本和测试样本的分布见表3。

表3 5类气阀故障模式信息
应用上述多分类器的故障诊断算法,编制Fortran95数值程序,实现了气阀故障诊断流程。先求出5类样本数据所对应的聚类中心,再对各类的聚类中心继续聚类生成二叉树的各个节点,最终得到形如图4所示的完全二叉树。图中C~G分别代表5个样本集,各类样本的模式标记见表3。

图4 气阀故障诊断的二叉树
依据所确定的二叉树结构,逐个训练4个支持向量机。在训练过程中,径向基核函数参数γ和惩罚参数C的选择十分重要,影响着向量机的分类性能。本文采用网格搜索的方法优化这两个参数,以正确率最高时的参数值作为最优值,各支持向量机的参数设置见表4。

表4 多分类向量机参数的设置
根据表中的参数分别对4个支持向量机进行训练,根据得到的多分类向量机对测试样本进行诊断。内环锯断故障的测试样本有1个被识别为正常工况,内环两瓣故障的测试样本均能正确识别,内环中环两瓣故障有2个样本分别被识别为内环两瓣和三环两瓣,三环两瓣故障有2个样本被识别为内环中环两瓣,正常工况的测试样本有一个被识别为内环锯断故障,各类样本的识别准确率见表5。

表5 不同故障的诊断结果 (%)
该诊断结果表明本文构建的二叉树向量机对基于振动监测数据的气阀故障诊断效果较好。另由表中结果,结合模糊聚类的二叉树向量机比“一对多”向量机的诊断正确率更高。
4 结语
本文引入模糊C均值聚类和支持向量机方法构建了一种二叉树结构的多分类器,UCI数据集的分类结果表明其具有较高的分类准确性。对某往复压缩机气阀故障模拟试验的振动数据进行故障模式识别的结果表明,该方法有效实现了气阀故障的准确诊断。与传统的“一对多”向量机方法相比,本文方法的准确性更高。
——基于二叉树的图像加密

