基于深度置信网络的齿轮箱智能诊断方法

段礼祥， 赵剑平， 曲海涛， 张德军， 秦天飞

(1.中国石油大学(北京)安全与海洋工程学院， 北京 102249； 2.中国石化胜利油田分公司地面工程维修中心， 东营 257000； 3.中国石油塔里木油田分公司， 库尔勒 841000)

齿轮箱是机械设备中传递动力和改变转速的部件，长时间处于高温、高负荷的运行状态中。在持续冲击下，其零件很容易发生故障。油田现场环境复杂，采集到的齿轮箱振动信号包含大量的干扰，常淹没在噪声之中。因此，在强噪声环境下，准确、有效提取齿轮箱的故障特征，是提高诊断准确率的有效途径。其中，基于模态分解的方法得到了广泛的关注，经验模态分解(empirical mode decomposition，EMD)和局部均值分解(local mean decomposition，LMD)属于传统的递归式信号分解方法，广泛应用于信号分解和特征提取领域，但其包络估计误差经过多次分解会被放大，从而出现模态混叠[1]，无法将频率相近的分量进行有效分离。变分模态分解(variational mode decompostion,VMD)是非递归式信号分解方法，在获取分解分量的过程中通过迭代搜寻模型的最优解来确定每个分量的频率中心及频带的带宽，从而能够实现信号在频带上的有效分离[2]。白堂博等[3]提出基于VMD和奇异值分解(singular value decomposition，SVD)的信号降噪方法，首先对振动信号进行VMD分解，然后对每个模态进行SVD降噪，最后选取故障特征分量进行时、频域及包络谱分析，确定故障类型。张超等[4]将振动信号进行VMD分解，并计算每个模态的能量熵输入到支持向量机(support vector machine，SVM)分类器中进行故障分类。

MCKD是由Mcdonald等[5]在最小熵反褶积的基础上提出，以最大相关峭度为目标，对信号进行解卷积运算，突出淹没在噪声信号中的周期性冲击成分，已成功运用到了轴承和齿轮的故障诊断中[6-7]。

SVM和人工神经网络(artificial neural network，ANN)是应用较为广泛的浅层分类器，但存在局部最优解、收敛速度慢、耗时长等缺点[8]。Hinton等[9]首先提出了基于特征的深度学习，通过构建深层网络模拟人类大脑逐层学习的模型和过程，直接从原始数据形成认识与判断，避免传统特征提取过程的复杂和不确定性，增强模式识别的智能性。深度置信网络(deep belief network，DBN)以其快速推理，编码更丰富、更高阶网络结构的优势成为一种非常流行的深度学习模型。DBN表征信号与特征之间复杂的映射关系，非常适合复杂非线性、高维度数据的特征挖掘。目前，DBN已成功运用于语音、文字和图像识别等领域，并在故障诊断领域得到初步应用[10]。

针对强噪声干扰下，难以精确诊断齿轮箱故障的问题，提出了基于VMD-MCKD和DBN的齿轮箱智能诊断方法，运用VMD和MCKD对振动信号进行降噪滤波，凸显信号中的故障冲击成分，降低噪声信号的干扰。将传统的故障诊断方法和深度学习相结合，实现齿轮箱故障特征自适应挖掘与故障模式的智能识别。

1 理论方法

1.1 变分模态分解

变分模态分解构造的变分问题为：各模态之和等于输入信号f，寻求k个模态函数，使得每个模态函数的估计带宽之和最小[11]。定义一个幅值为Ak(t)、频率为ωk(t)的调频-调幅信号：

uk(t)=Ak(t)cos[φk(t)]

(1)

式(1)中：uk(t)是谐波信号；Ak(t)是信号的瞬时幅值；φk(t)是信号的相位。

VMD引入二次惩罚因子和拉格朗日乘法算子，将约束性变分问题变为非约束性变分问题，二次惩罚因子在随机噪声存在的情况下保证信号的重构精度，拉格朗日乘法算子加强约束条件严格性。拉格朗日表达式为

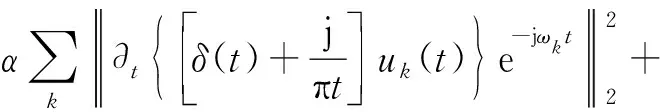
(2)

式(2)中：ωk(t)为频率；λ为拉格朗日乘法算子；α为二次惩罚因子；δ(t)为单位脉冲函数；f(t)为输入信号。

1.2 最大相关峭度解卷积

最大相关峭度解卷积通过构造有限冲击响应滤波器，使原始信号通过滤波后相关峭度达到最大，从而突出被噪声掩盖的周期性冲击成分。选取一个最优滤波器f(l)，使相关峭度CKM(T)最大：

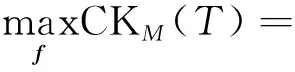
(3)

式(3)中：yn为周期性冲击信号；T为冲击信号周期；M为位移数；L为滤波器的长度；f为滤波器向量。

1.3 深度置信网络

深度置信网络是由多个受限玻尔兹曼机(restricted Boltzmann machine，RBM)和一个Softmax分类器堆叠而成的多隐含层神经网络，运用逐层贪婪学习算法优化深层神经网络的权重和偏置[12]。通过建立观测数据与标签数据之间的联合分布，从低层到高层挖掘数据特征。

1.3.1 前向堆栈RBM训练

RBM模型如图1所示，包含可视层和隐含层两层神经元，层间神经元双向连接，层内神经元无连接。

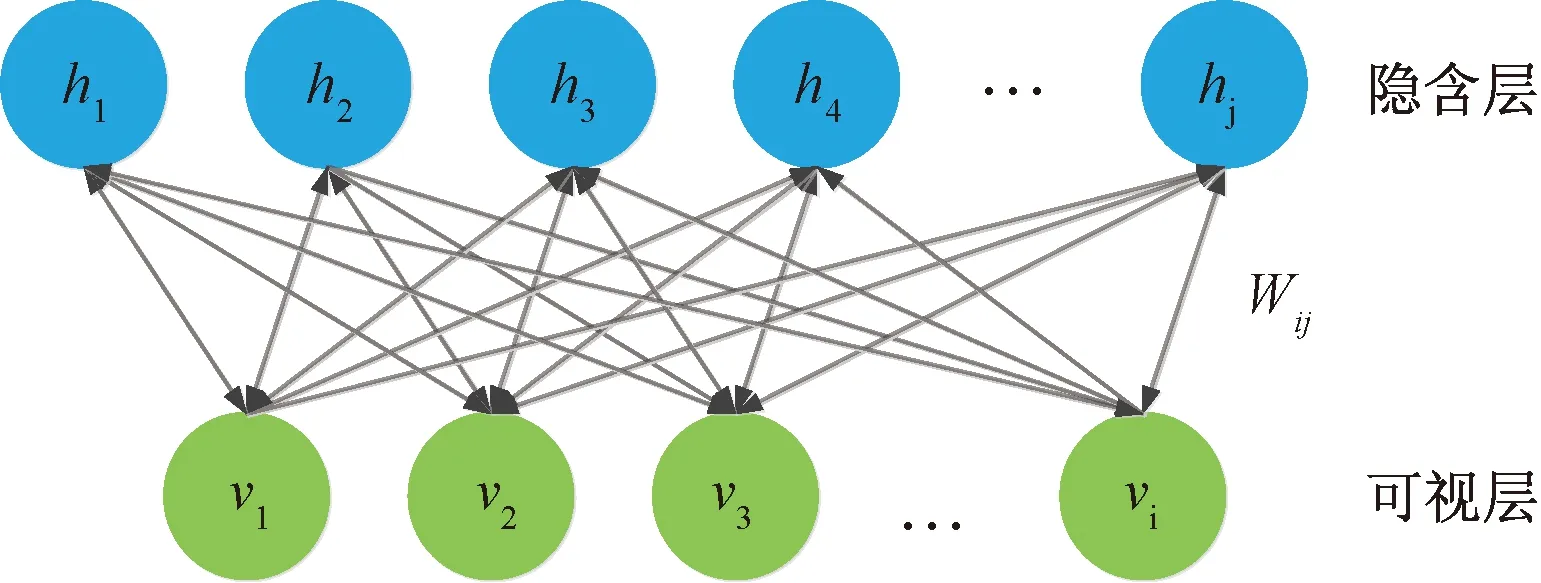
vi为可视层神经元；hj为隐含层神经元；wij为连接权重图1 RBM模型Fig.1 RBM model

RBM是一种基于能量的随机神经网络[13]。可视层神经元v与隐含层神经元h联合状态(v,h)的能量函数定义为

(4)

式(4)中：I为可视层神经元的数量；J为隐含层神经元的数量；wij为可视层vi和隐含层hj的连接权重；ai和bj分别为可视层和隐含层的偏置。

RBM模型各隐含层节点的激活状态是相互独立的，第j个隐含层节点的激活函数为

(5)

(6)

在给定可视层向量v后，通过式(5)计算隐含层单元h的状态，通过式(6)得到重构可视层单元v的状态。当可视层单元和重构可视层单元之间的误差最小时，隐含层单元就可以作为可视层输入单元的特征提取结果，从而使网络达到了特征提取的目的。RBM训练求得最接近训练样本的联合概率分布，更准确地还原特征，寻找可视层节点和隐含层节点之间最优连接权重和偏置。

1.3.2 反向传播训练

反向传播训练降低训练误差，提高DBN模型的分类准确率。反向传播训练考虑所有层神经网络，使用模型输出和标签数据计算训练误差。DBN网络参数被更新，以最小化训练误差[14]。反向传播过程持续到网络输出达到最大迭代次数，预训练的DBN模型通过反向微调进一步提高分类准确率。

2 基于VMD-MCKD和DBN的齿轮箱智能诊断方法

基于VMD-MCKD和DBN的齿轮箱智能诊断方法的步骤如下。

(1)将采集到的齿轮箱振动信号进行VMD分解，观察中心频率确定最佳模态分解效果。

(2)计算分解各模态与原信号的互相关系数δ，滤去δ<0.1的分量，保留δ>0.6的分量。

(3)将0.1≤δ≤0.6的分量进行MCKD降噪，根据采样频率和故障频率确定解卷积周期，试验确定最佳位移数和滤波器长度，达到最佳降噪效果，最后将降噪信号与δ>0.6的分量重构。

(4)将重构信号进行归一化预处理，划分训练集和测试集，初始化DBN权重和偏置，设定深层神经网络的超参数，进行前向堆栈RBM训练和反向传播训练，达到全局性能最优，实现故障特征的自适应提取。

(5)将测试集输入到训练好的DBN网络模型中，实现齿轮箱故障特征自适应挖掘与故障模式智能识别，输出故障诊断结果。

3 工程应用

以塔里木油田某往复式注水泵传动齿轮箱为研究对象，齿轮箱输入轴转速1 450 r/min，转动频率fr=24.17 Hz，主动轮齿数30，从动轮齿数65，采样频率42 240 Hz，采样点数32 744。振动信号测点位于输入轴轴承座竖直方向，如图2所示。

在现场经过长期监测，获取齿轮箱在正常、齿面磨损、齿根裂纹和轮齿断裂4种运行状态下的振动信号进行实验。图3为齿轮箱振动信号时域波形。

VMD需事先设定分解模态数k，以轮齿断裂状态下的故障信号为例进行自适应VMD分解，通过设定不同模态数求得的中心频率如表1所示。

图2 测点位置Fig.2 Location of measuring point

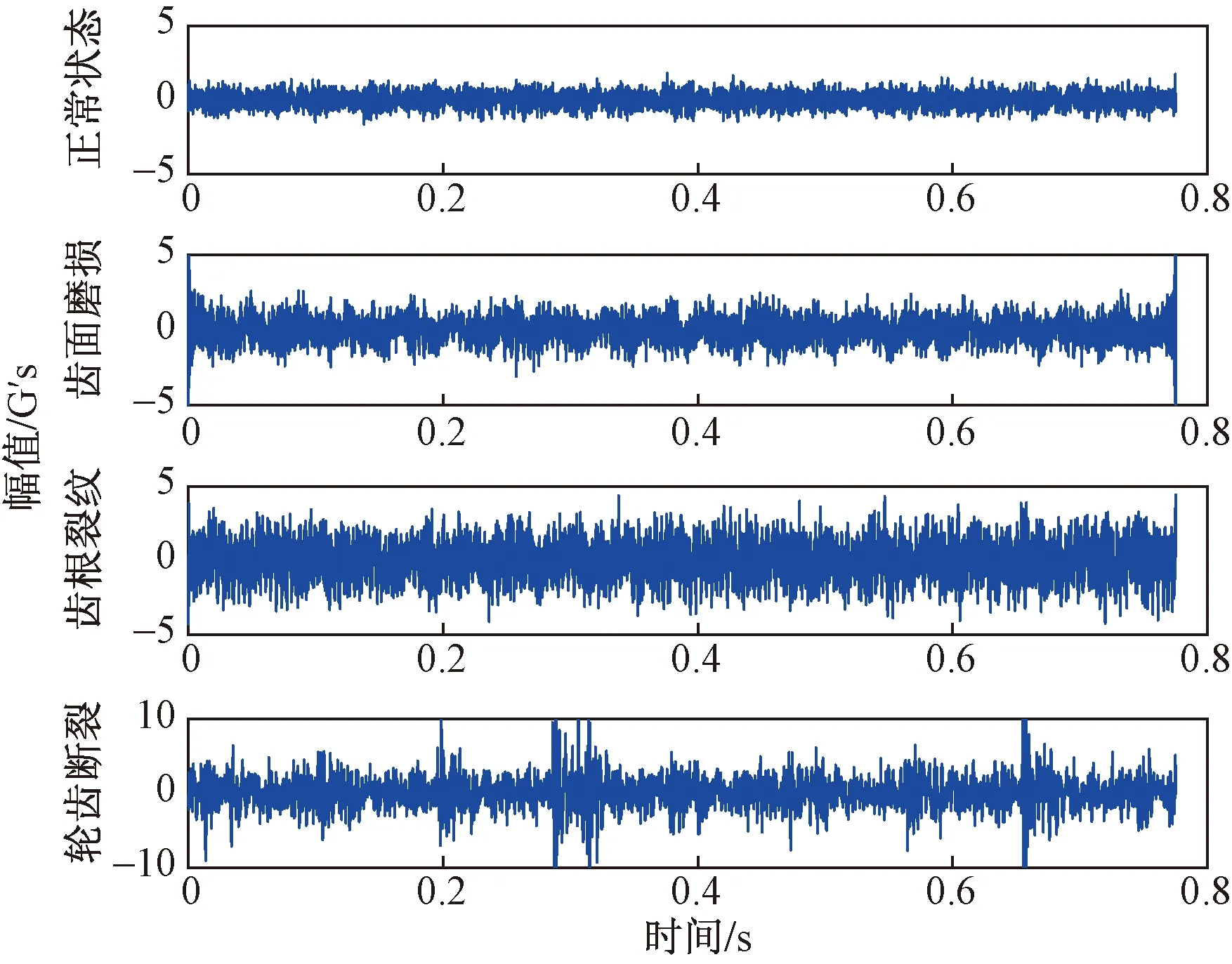
1 G′s=9.8 m/s2图3 振动信号时域波形Fig.3 Time domain waveform of vibration signal

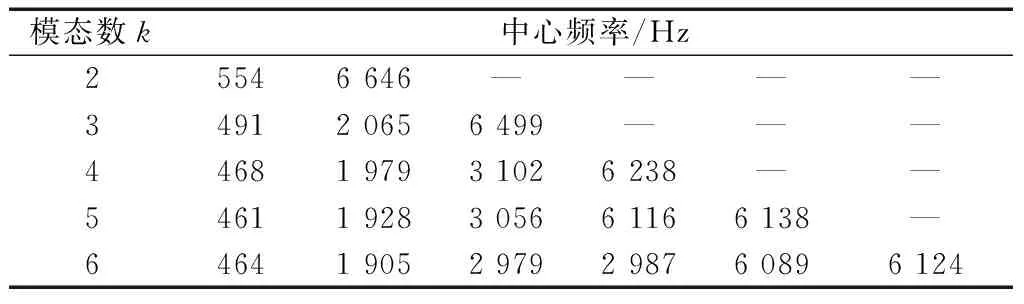
表1 中心频率

由表1可知，当k≥5时，出现了6 116、6 138、2 979和2 987 Hz频率相近的分量，信号分解产生过分解，因此确定最佳的模态分解数为4，多次试验确定惩罚因子α=2 000。图4为轮齿断裂运行状态下的振动信号经过VMD分解后的时域波形，其中本征模态函数(intrinsic mode function，IMF)是分解后的固有模态分量。图5为分解分量经过傅里叶变换的频谱图，截取的频率范围为0～8 000 Hz。

求解4种运行状态下分解后各模态分量信号与原始信号的互相关系数δ，如表2所示。滤去互相关系数<0.1的模态，将互相关系数>0.6的模态直接用作降噪后的信号重构。

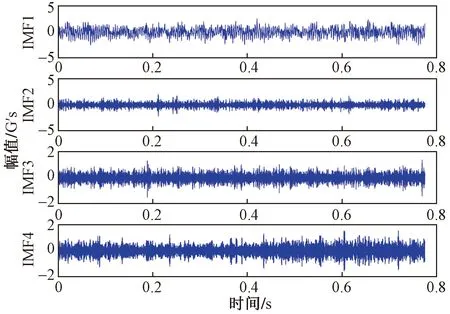
1 G′s=9.8 m/s2图4 VMD分解后时域波形Fig.4 Time domain waveform after VMD decomposition

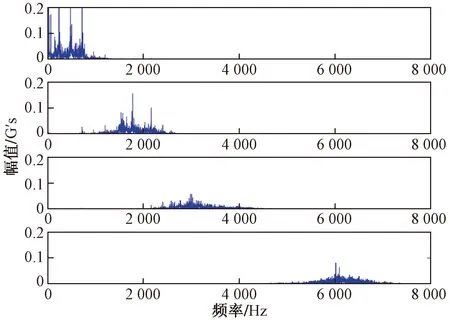
1 G′s=9.8 m/s2图5 VMD分解后频谱图Fig.5 Spectrum after VMD decomposition

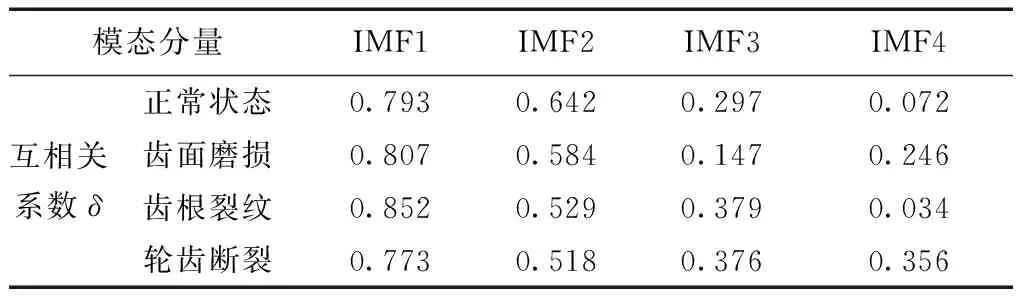
表2 互相关系数

对0.1≤δ≤0.6的分量进行MCKD降噪处理，根据采样频率和故障频率求得解卷积周期为T=fs/fr=42 240 Hz/24.17 Hz=1 750，试验确定位移数M=7，等步长搜索确定滤波器长度L=640。以轮齿断裂运行状态下振动信号经过VMD分解后的模态分量为例进行MCKD降噪，轮齿断裂-IMF2与降噪后信号的对比如图6所示。可以看出模态分量经过降噪处理后，信号的周期性冲击特征凸显出来，证明降噪效果良好。降噪后信号的频谱如图7所示，齿轮转动频率fr和啮合频率fm两种频率的倍频及其谐波凸显出来，进一步证明方法具有良好的降噪效果。

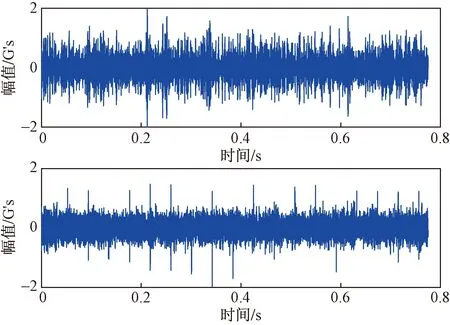
1 G′s=9.8 m/s2图6 轮齿断裂-IMF2与降噪后的信号对比Fig.6 The signal contrast between gear fracture-IMF2 and denoise component

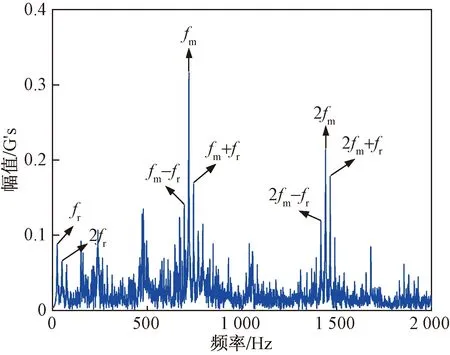
图7 降噪信号频谱Fig.7 Spectrum of denoise signal

将δ>0.6的分量与降噪信号进行重构，用于构造DBN网络模型输入的特征数据集。

首先对重构信号进行线性归一化预处理，使其保持在[0,1]。输入轴的转速为1 450 r/min。为保证每个数据样本有1个转动周期以上的数据点数，设定特征集数据样本的长度为2 000，对每类故障数据截取1 000组数据样本构造特征矩阵并定义数据标签。构造不同比例的数据集如表3所示。

表3 数据集描述

将构造的训练集输入到DBN网络中进行模型训练。DBN网络结构选用经典的5层结构，包括输入层、3个隐含层和输出层，输入层节点数由样本特征维度决定，输出层节点数由分类数决定，网络结构设定为2 000-500-120-20-4。由于数据样本较长，故RBM训练的迭代次数设定为600，学习速率e为0.5，动量参数τ为0.9，以加快网络训练的速度。

首先用堆栈RBM网络初始化整个模型训练的权重和偏置值，然后作为DBN反向微调的初始的权重和偏置，利用梯度下降法不断更新该权重和偏置值，每迭代10次后计算一下故障信号的分类准确率。最后，用最终训练好的权重和偏置值对划分好的测试集进行分类。在反向微调过程中，分别用Isigmoid、Sigmoid、Tanh和LRelu函数作为激活函数的故障分类准确率如表4所示。

表4 四种激活函数下的故障分类准确率

由表4可知，DBN的反向微调训练过程中运用Isigmoid函数作为反向微调的激活函数时，其故障诊断准确率明显高于其他函数，训练准确率和测试准确率之间的差异也最小，整个网络模型具有较高的稳定性和较快的收敛速度，解决了其他3种激活函数进行网络训练时产生的梯度消失问题。

t分布随机领域嵌入(t-distributed stochastic neighbor embedding，t-SNE)是一种非线性特征降维算法，其基本思想是将高维空间数据点映射到低维空间，保持高维空间数据点和对应的低维空间数据点之间的特性不变，非常适用于将高维空间的数据降维至二维或三维空间数据，然后对低维空间数据进行可视化，达到理想的降维效果。为了验证DBN模型的特征提取能力，分别选用表3所示的不同百分比训练集和测试集输入到DBN模型中进行训练。基于t-SNE特征降维和可视化效果如图8所示。

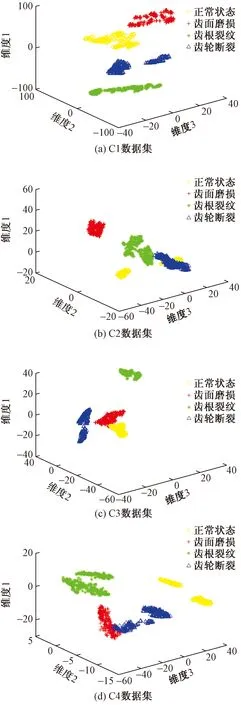
数据无量纲图8 特征提取可视化图Fig.8 Feature extraction visualization

由图8可知，随着训练集比例的增加，三维空间内故障特征分布的范围逐渐缩小，产生聚类效果，不同故障特征分布的距离逐渐增大，故障分类准确率也显著提高。

为了验证本文方法的故障诊断效果，分别与EMD-DBN、EMD-SVM、DBN、SVM分类模型进行对比实验，随着迭代次数增加分类准确率的变化如图9所示。

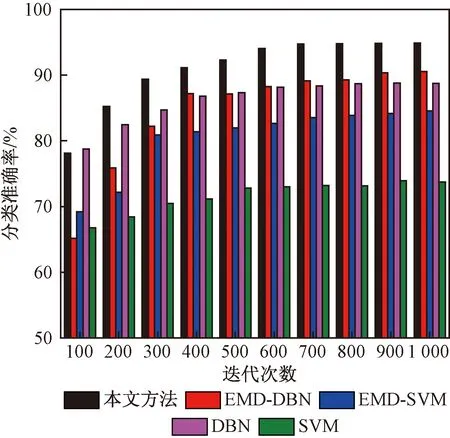
图9 分类准确率Fig.9 Classification accuracy

由图9可知，本文方法相比其他4种分类模型始终保持较高的分类准确率，具有更好的稳定性。随着网络训练迭代次数的增加，分类准确率明显提高。迭代次数达到600后，分类准确率基本保持不变，但网络训练所需时间显著增加，严重影响故障诊断的效率。因此，在进行深层网络模型训练的过程中，应合理选择迭代次数，保证模型的实用性，防止网络训练出现过拟合的现象。

4 结论

提出基于变分模态分解-最大相关峭度解卷积和深度置信网络的齿轮箱故障智能诊断方法，并通过油田现场的实际应用，验证了方法具有很好的鲁棒性和实用性，对油田的故障诊断工作具有指导意义。主要结论如下。

(1)VMD通过迭代搜寻确定最佳的中心频率和频带宽度，实现故障信号和噪声信号在不同频带上的有效分离；MCKD以最大相关峭度为目标，通过多次迭代实现信号的解卷积运算，增强被强噪声掩盖的故障周期性冲击成分，故障特征频率凸显。

(2)基于VMD-MCKD和DBN的齿轮箱智能诊断方法将传统故障诊断方法和深度学习相结合，通过对原始信号进行降噪滤波和深层网络模型训练，实现了故障特征自适应挖掘与故障模式的智能识别，达到了较高的分类准确率。

(3)通过增加网络模型的训练集比例，故障特征分布范围逐渐缩小，聚类效果增强，随着网络迭代次数的增加，故障分类准确率显著提高，且高于文中其他几种分类模型，但应合理选择网络训练迭代次数，保证模型的应用效果。