基于无迹卡尔曼滤波和协方差交叉融合的分层多簇无线传感器网络多速率跟踪算法

许红香， 白星振， 董礼廷， 张金昌

(山东科技大学电气与自动化工程学院， 青岛 266590)

目标跟踪是无线传感器网络(wireless sensor networks，WSNs)最具代表性和基础性的应用之一[1-4]。大量的微型传感器节点部署在监测区域内，通过无线通信方式形成一个多跳的自组织的网络系统，这个系统被称为WSNs[1,3]。随着人工智能领域的飞速发展，目标跟踪问题得到了越来越多的关注，几乎涉及WSNs的各个应用领域，如环境监测、军事监控和基建保护等，体现了巨大的科学意义和应用前景[3]。WSNs具有灵活部署、消耗低、容量小、应用范围广等优点，但是也受到电池容量、计算能力和通讯带宽的影响[4]。传统的WSNs是通过每个传感器节点在网络上共享信息，一起完成复杂的工作[1]。然而，在实际应用中，随着传感器覆盖范围的不断扩大，每个传感器都与融合中心进行通讯是不现实的。多个传感器在短时间内与光纤进行通信，会造成资源浪费、信道阻塞等问题[5]。针对这一问题，将网络中的所有传感器划分为多个簇，同一簇内的传感器连接到同一簇头(cluster head，CH)节点，作为局部估计量，并预先由CH节点对每个簇的采样信息进行预处理，不同簇的CH节点与融合中心相连接，然后将局部估计值上传到融合中心[6-7]。

文献[8]提出多传感器数据融合中各个传感器以相同的采样和传输速率进行数据的采集和传输。但是，在实际应用中，随着传感器系统规模的扩大，传感器固有延时和通信延时，不同的传感器的采样和传输速率往往不同[9]。因此，传感器可以采用不同的采样和传输速率进行数据的采集、传输，将数据发送到局部估计器，进而发送到融合中心。文献[10]研究了卡尔曼滤波(Kalman filter，KF)模型的多传感器数据融合定位技术，文献[11]提出一种基于改进KF的姿态解算法，文献[12]将卡尔曼一致性滤波应用于目标跟踪中。然而，KF只能处理线性系统，针对非线性系统的性能很差。针对这个问题，文献[13]提出扩展卡尔曼滤波(extended Kalman filter，EKF)，EKF是基于一阶非线性系统的一阶泰勒级数展开，一般对线性或者弱非线性系统有较好的结果。针对强非线性系统效果降低。因此，Julier等提出了无迹卡尔曼滤波(unscented Kalman filter，UKF)，UKF是对非线性函数的概率密度进行近似，不需要计算雅克比矩阵，一般可达二阶，甚至三阶精度，有效的克服了KF、EKF在非线性系统中估计精度低、稳定性差等缺点[14-15]。

基于以上分析，提出基于UKF和协方差交叉(covariance intersection，CI)融合的分层多簇WSNs多速率跟踪算法。传感器节点采用不同的采样和传输速率进行数据的采集和传输，同一簇中的传感器可以互相通信，将收集到的测量值生成局部估计，局部估计采用UKF。融合中心利用CI融合算法将局部估计值生成融合估计。CI融合算法可以避免互协方差矩阵的计算，降低计算的复杂度。

1 系统模型

考虑二维空间目标跟踪的匀速运动模型[16]，状态方程为

x(tk+1)=Fx(tk)+Gω(tk)

(1)

(2)

式中：x(tk)=[xp(tk),xv(tk),yp(tk),yv(tk)]；xp(tk)和yp(tk)分别为目标在x轴和y轴的位置；xv(tk)和yv(tk)分别为目标在x轴和y轴的速度；F、G为适当维数的时变矩阵；Δtk=tk+1-tk为时间间隔，可以根据WSNs的功率状态和目标的性能需求在线确定；ω(tk)=[ωx(tk),ωy(tk)]T为均值为0的高斯白噪声。满足如下条件：

E[ω(tk)]=0

(3)

E[ω(tk)ωT(tl)]=Q(tk)δkl

(4)

式中：E期望；Q(tk)为状态噪声协方差矩阵。δ狄拉克函数，当k=l时，δkl=1，否则，δkl=0。初始状态x(0)是一个随机变量，满足：

E[x(0)]=x0

(5)

E{[x(0)-x0][x(0)-x0]T}=P0

(6)

式中：x0和P0为初始状态的均值和协方差矩阵。

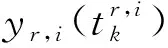
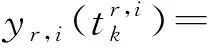
i=Mr,r∈Z0

(7)

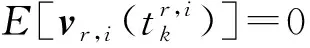
(8)

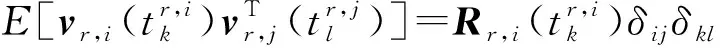
(9)

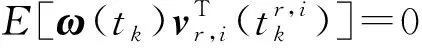
(10)

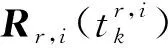
为了便于理解，图1表示Mr-1和Mr中各个传感器采样率之间的关系，其中r>1。假设Mr-1和Mr中各包含3个传感器，在Mr-1中，Ξr,1具有最高采样率，Ξr,3具有最低的采样率，Ξr,2采样率在两者之间。而在Mr中，Ξr,1具有最高采样率，Ξr,2和Ξr,3采样率相同且低于Ξr,1，多速率采样示意如图1所示。

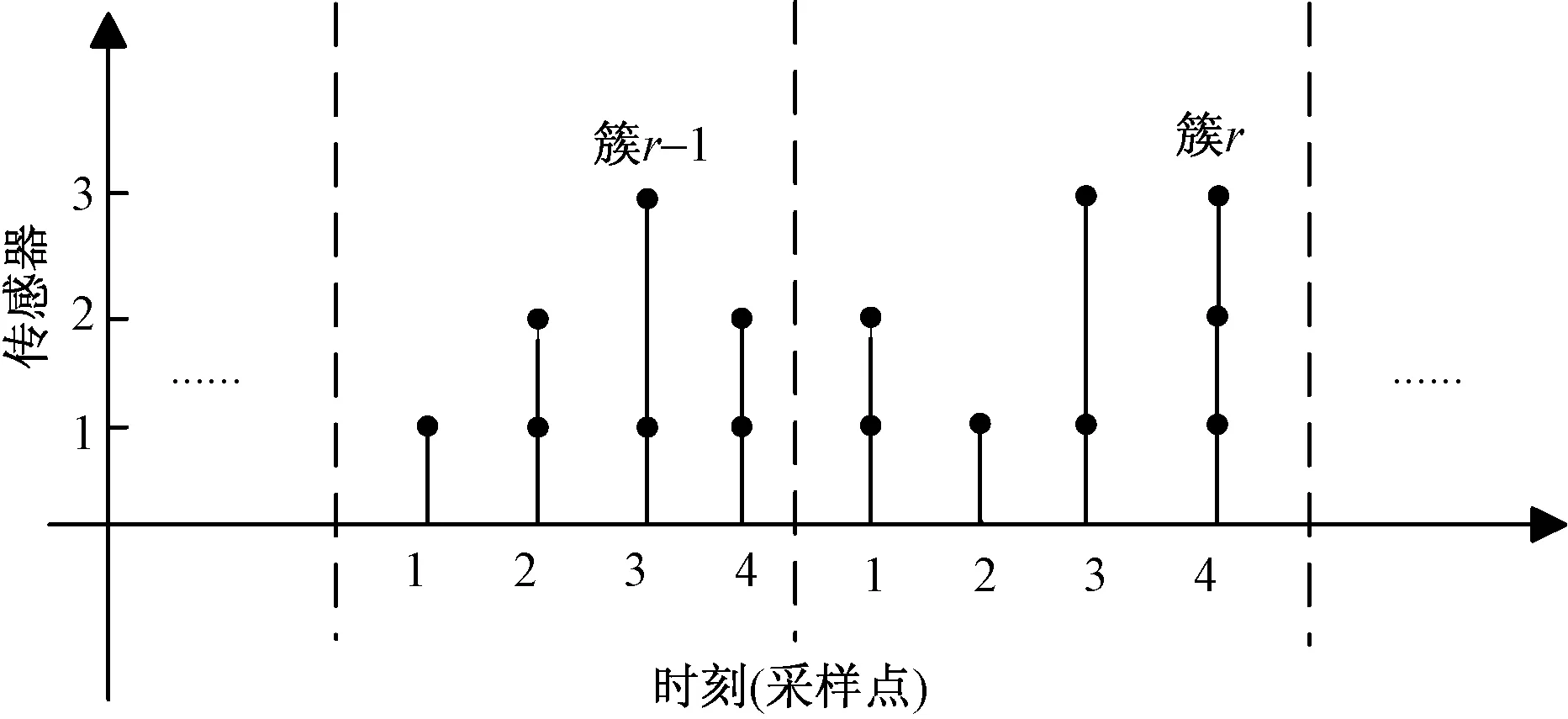
图1 多速率采样示意图Fig.1 Schematic diagram of multi-rate sampling

2 分层融合

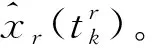
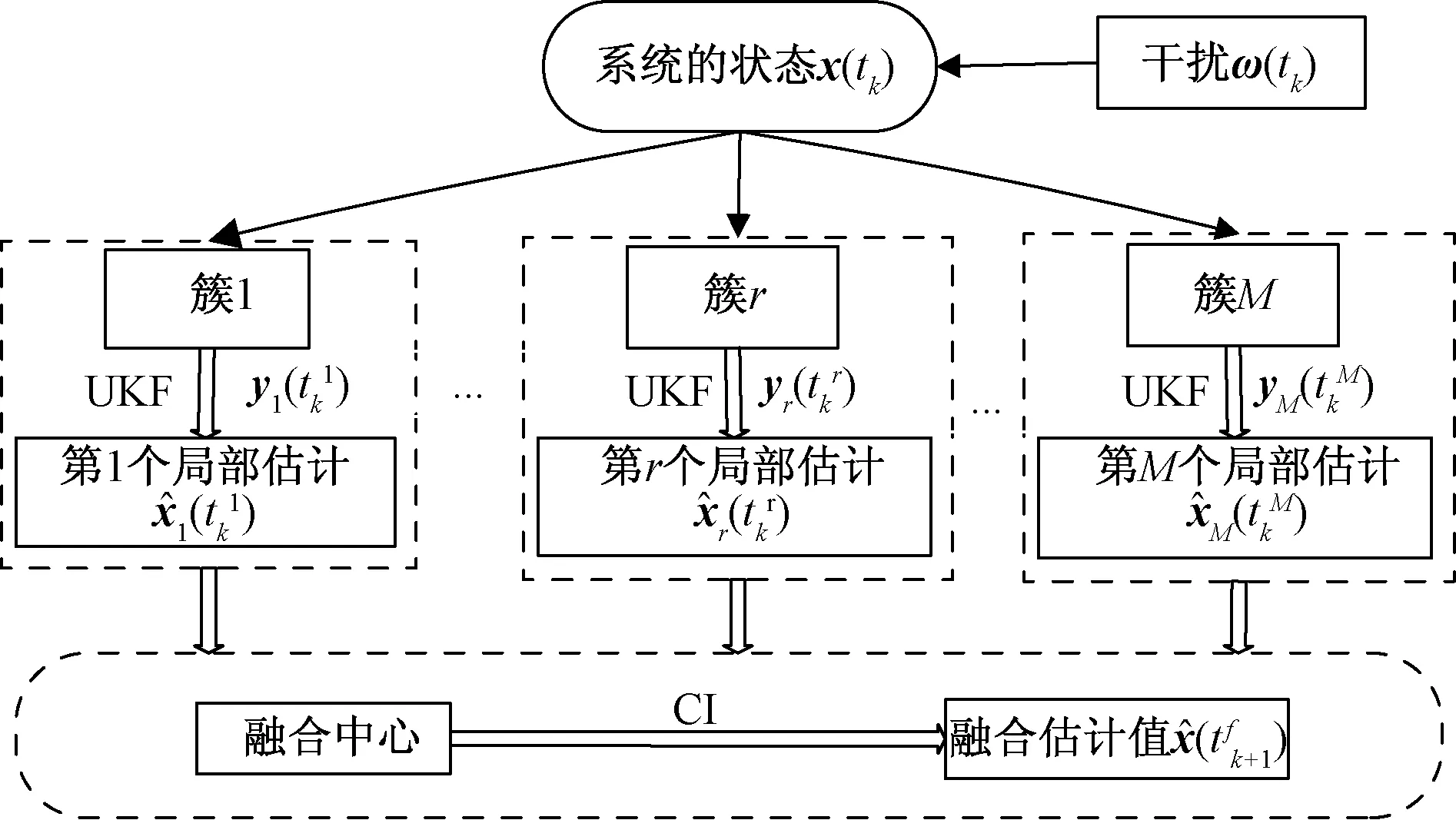
图2 分层融合算法结构图Fig.2 Hierarchical fusion algorithm structure diagram

2.1 局部UKF

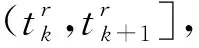
2.1.1 UKF初始化

设置初始状态x0和初始误差协方差矩阵P0。

2.1.2 预测

计算2L+1个sigma点，即采样点，这里的L指状态的维度。

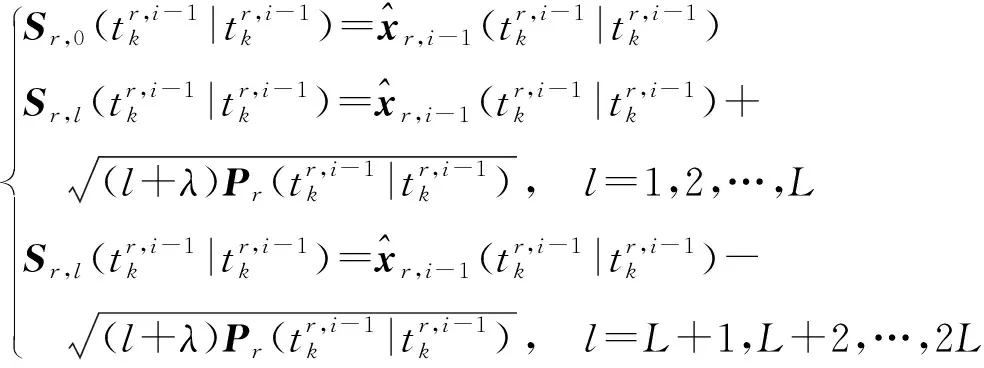
(11)

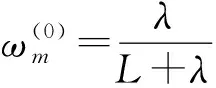
(12)

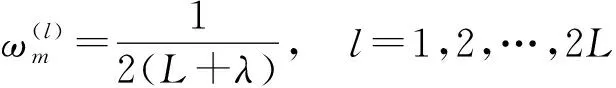
(13)

式中：λ=α2(L+ξ)-L；α和ξ为两个可调参数。

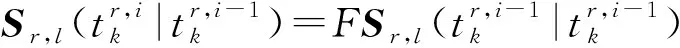
(14)

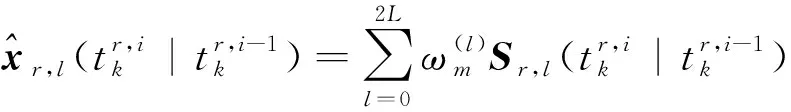
(15)

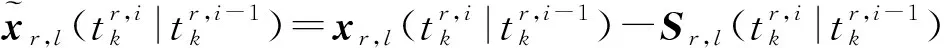
(16)

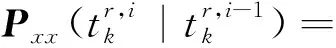
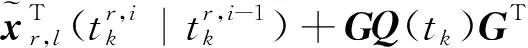
(17)

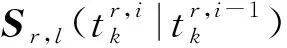
2.1.3 量测更新

计算量测预测值及加权求和得到的预测的均值。

(18)

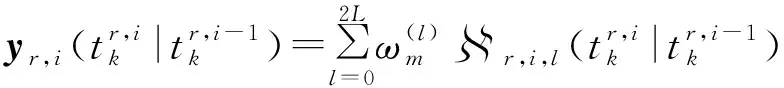
(19)

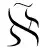
(20)

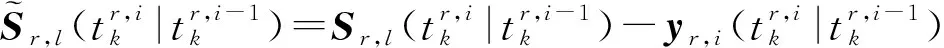
(21)

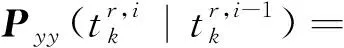
(22)

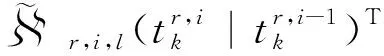
(23)

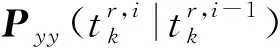
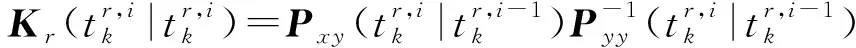
(24)

状态更新值以及协方差更新如下：

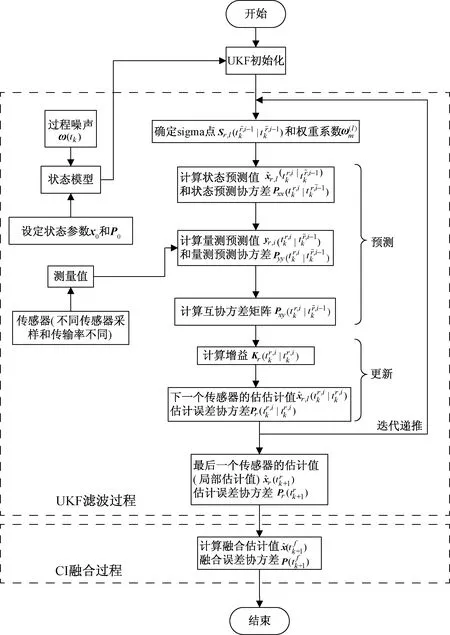
图3 分层融合估计流程图Fig.3 Flow chart of hierarchical fusion estimation

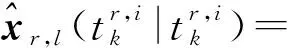
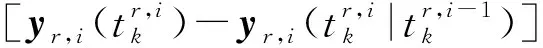
(25)

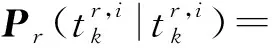
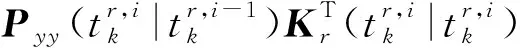
(26)

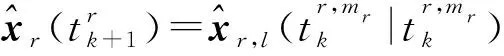
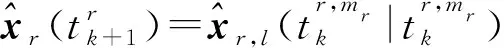
(27)

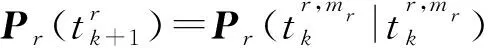
(28)

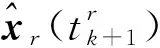
2.2 融合算法

由于簇中的传感器有不同的采样和传输速率，因此计算局部估计之间的互协方差矩阵是非常困难的，并不适合真实的应用场景。CI融合算法可以看作基于局部估计的一个凸组合[12]，只使用局部估计和局部估计协方差产生融合估计，利用CI融合算法不需要计算互协方差矩阵的优势，来降低计算的复杂度。分层融合估计流程图如图3所示。

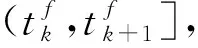
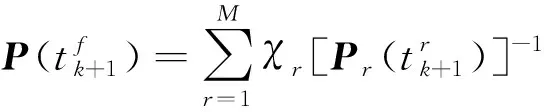
(29)

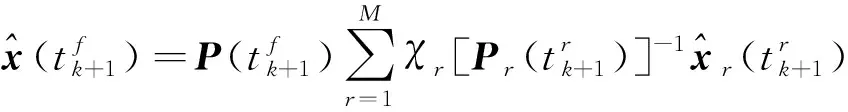
(30)

根据均方误差意义下的最优性，即

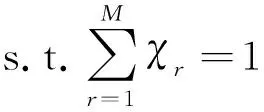
(31)

权重系数由次优法中相应的对角项确定，以供实时考虑，即

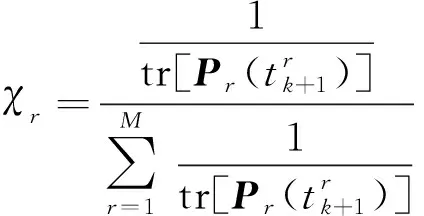
(32)

3 仿真验证

通过传感器采集的目标数据进行融合来证明算法的有效性，将传感器分成4个簇，分别为M1、M2、M3、M4。其中，M1包含3个传感器，M2包含4个传感器，M3包含5个传感器，M4包含6个传感器。假设不同簇的传感器的噪声不同，设置M1的3个传感器的噪声协方差为R1=0.02，M2的4个传感器的噪声协方差为R2=0.015，M3的5个传感器的噪声协方差为R3=0.01，M4的6个传感器的噪声协方差为R4=0.03，设置目标的过程噪声协方差为Q=10-3diag(0.05,0.1)，不同传感器的采样间隔各不相同，仿真结果如图4～图7所示。

均方根误差(root mean square error, RMSE)定义为

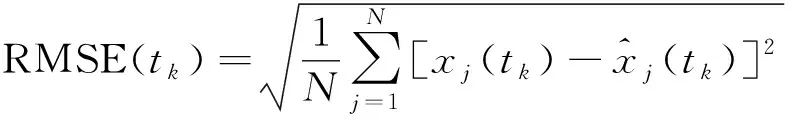
(33)

均方根误差和(sum of root mean square error, SMSE)定义为

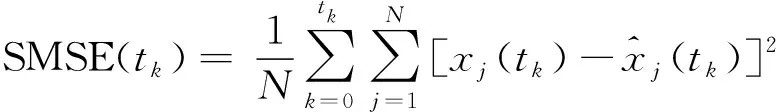
(34)

式中：N表示仿真次数，设置为N=100；tk表示在tk时刻第j次仿真的估计值。

为了提高估计的精度，采用多速率融合算法进行数据的融合。图4所示为真实轨迹、局部估计和融合估计轨迹的RMSE和SMSE对比，相比局部估计得到的轨迹，在融合阶段通过CI融合算法得到的轨迹更接近于真实轨迹，说明融合估计精度更高。图5为局部估计和融合估计误差对比。与局部估计相比，融合估计得到RMSE最小，在0.1以内，说明融合估计的结果更好。同时，融合估计得到SMSE最小。

图6为UKF-CI和EKF-CI的RMSE和SMSE对比。从图6可以看出，UKF-CI估计的误差小于EKF-CI，结果表明本文方法效果更明显。

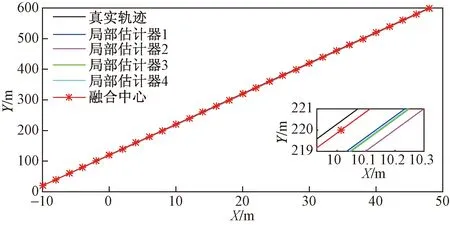
图4 真实轨迹、局部估计和融合估计轨迹对比Fig.4 Comparison of real trajectory, local estimation and fusion estimation

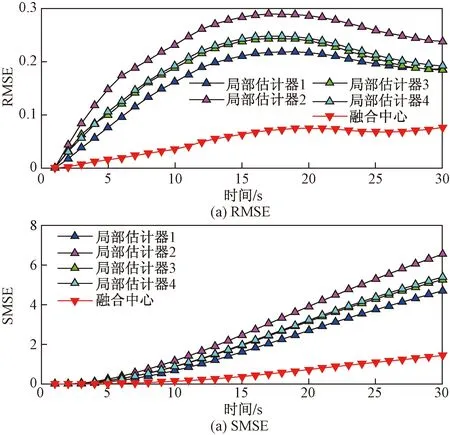
图5 局部估计和融合估计误差对比Fig.5 Error comparison of local estimation and fusion estimation

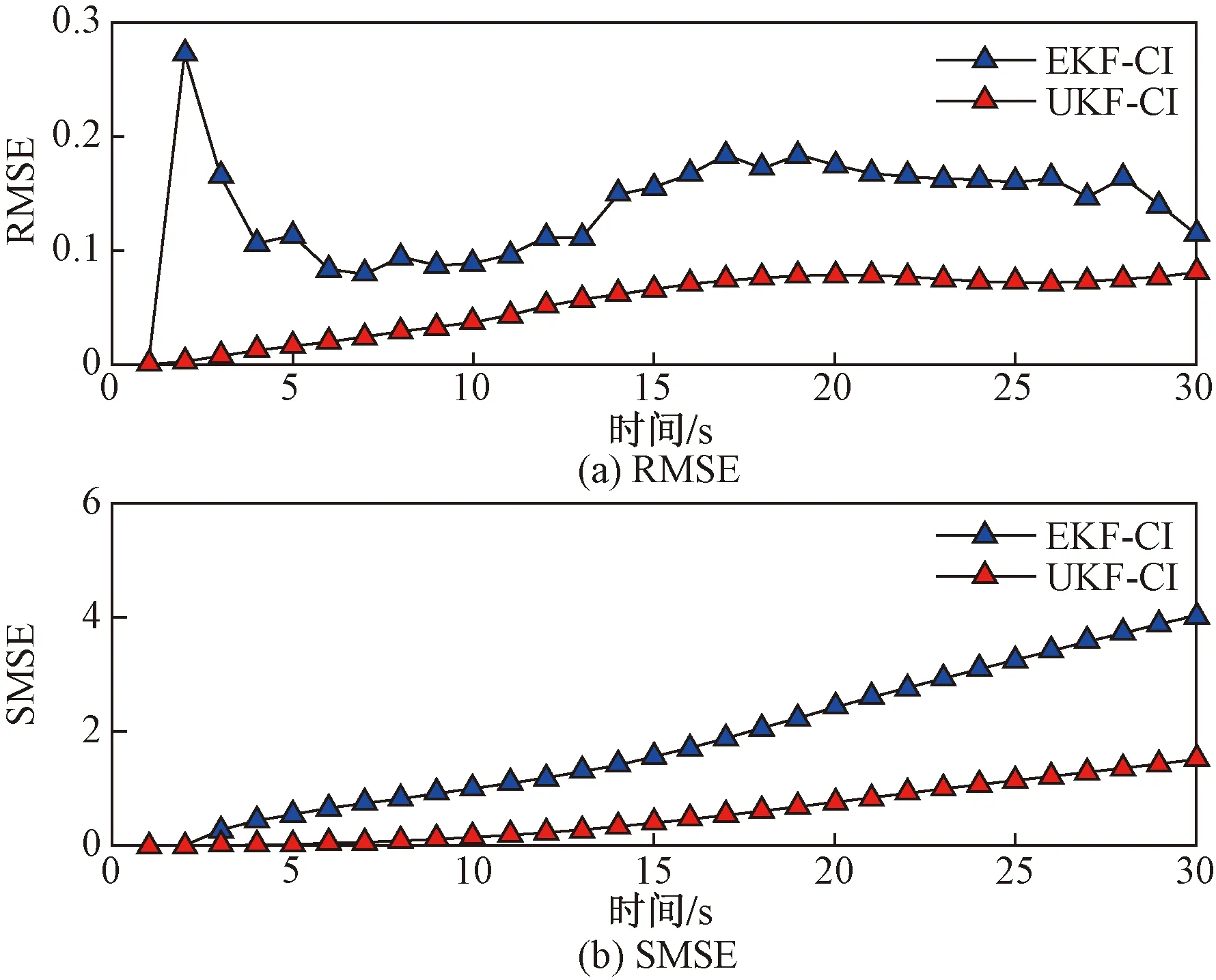
图6 UKF-CI和EKF-CI的误差对比Fig.6 Error comparison of UKF-CI and EKF-CI

图7为单速率和多速率RMSE和SMSE的比较。从图7可以看出，局部估计1-多速率的RMSE和SMSE低于传感器1-单速率。结果表明，采用多个采样和传输速率满足系统的性能需求。

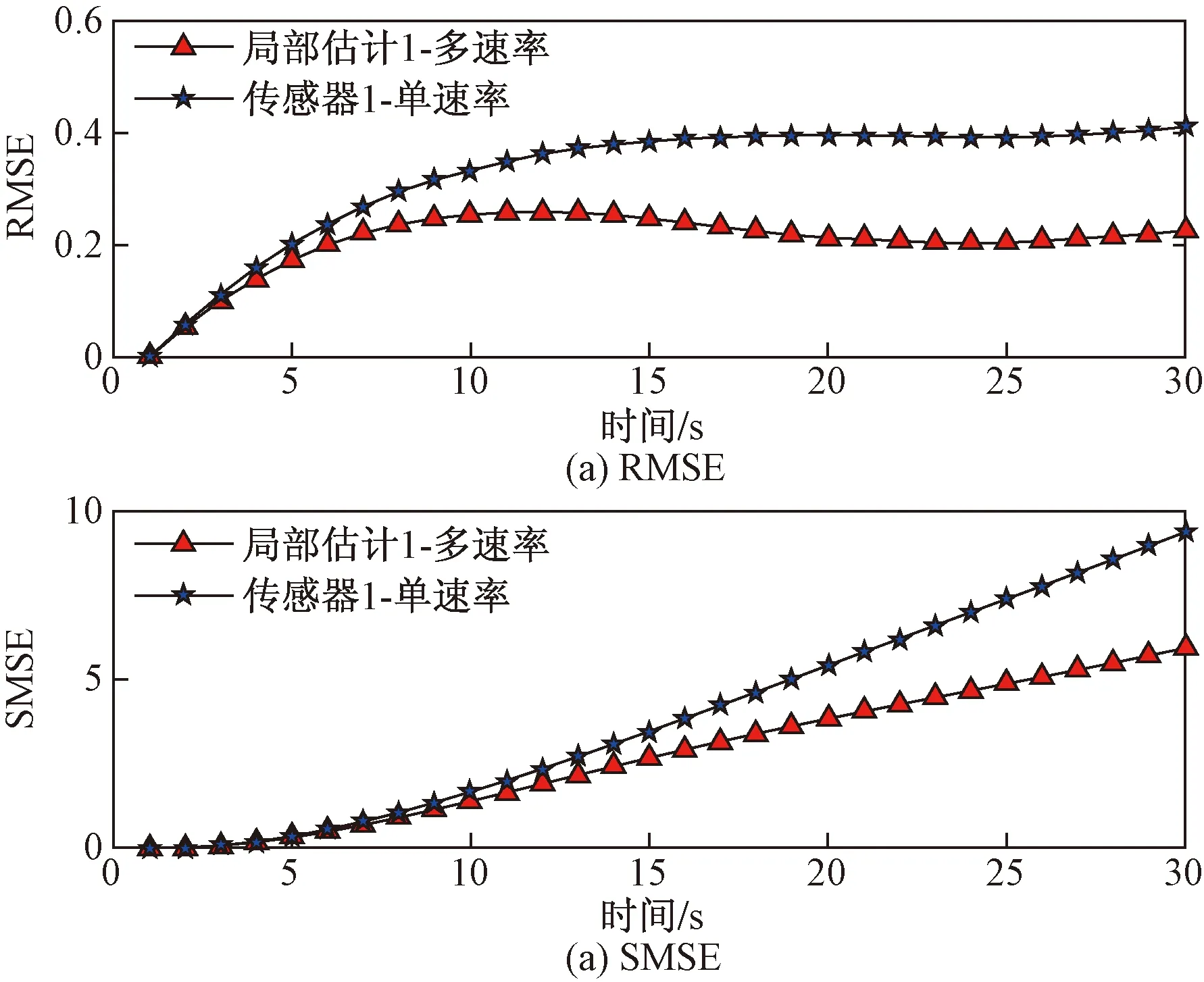
图7 单速率和多速率误差对比Fig.7 Error comparison of single-rate and multi-rate

4 结论

针对WSNs在定位跟踪过程中出现精度低、性能差的问题，提出分层多簇WSNs的多速率跟踪算法。仿真结果表明，与局部估计相比，采用UKF和CI融合算法得到的结果精度更高。UKF主要处理非线性问题且比EKF的计算复杂度低。CI融合算法不需要计算互协方差矩阵，因此可以进一步减少计算的复杂度。采用多个采样和传输速率满足系统的性能需求，相比EKF-CI，采用UKF-CI方法效果更好。