欠驱动航天器李雅普诺夫函数非线性姿态控制

夏德银

(北京控制与电子技术研究所,北京 100038)

1 引言

欠驱动机械系统是一类控制输入个数小于系统自由度的控制系统,它广泛地存在于机器人、航空航天等各个领域,由于控制输入个数的减小,较大地增加了系统的控制难度,因此它成为控制系统的研究热点之一.针对欠驱动机械系统,研究人员已经提出了较多的控制方法,例如文献[1]提出了基于能量的控制方法;文献[2-3]分别设计了基于神经网络补偿摩擦的奇异避免能量控制器以及基于模糊神经网络补偿摩擦的奇异避免能量控制器等.

欠驱动航天器是一类具有强非线性和强耦合性的复杂机械系统.针对欠驱动航天器的执行机构出现故障或者缺失的状况,已经出现了较多有价值的研究成果.文献[4]设计了分段解耦的姿态控制器,每一步解耦的前提是前面分段的控制误差要尽量地趋近于零;文献[5]给出了零角动量逆最优的稳定控制器,对输入不确定性具有一定的鲁棒性;文献[6]提出了反步控制器,只是所应用的运动学模型未考虑失控轴的角速度,给出的反应控制器存在奇异性,需要证明在奇异点姿态控制系统也是收敛的;文献[7]给出了一种复杂的连续时变控制律,通过引入辅助变量和设计中间虚拟变量使得系统的参数趋于稳定;文献[8]给出了零角动量逆最优的稳定控制器,对输入不确定性具有一定的鲁棒性;文献[9]采用路径规划获得开环最优控制输入和非线性预测控制方法(nonlinear model predictive control,NMPC)实现系统的反馈控制,给出的NMPC方法计算量较大,需要进一步提升系统的在线优化实时性;文献[10]将鲁棒变增益PID控制转化为双线性矩阵不等式可行解的问题,增大了计算量,增加了控制器求解的复杂度;文献[11]根据Pontryagin极小值原理将系统姿态运动跟踪问题转化为两点边界值问题,采用Legendre-Gauss-Lobatto将两点边值问题转换为一个线性方程组求解.

综上所述,研究结果表明欠驱动轴角速度快速收敛是航天器姿态系统稳定收敛的重要前提;具有奇异性的姿态系统控制器,需要证明在奇异点姿态控制系统也是稳定收敛的;奇异避免的反步控制器,通过构造结构复杂的理想姿态角速度避免控制器出现奇异性.由此本文提出了一种李雅普诺夫函数的非线性连续控制器:

1) 基于欠驱动刚体航天器动力学和运动学的一体化模型,考虑失控轴的角速度,设计了李雅普诺夫函数的非线性控制器,利用三通道之间的强耦合性实现了驱动轴角速度和欠驱动轴角速度在较短的时间内快速地收敛到稳定状态.

2) 通过构造合适的李雅普诺夫函数及其一阶导数的变化控制律,推导得到了李雅普诺夫函数的非线性连续控制器.

3) 构造的李雅普诺夫函数及其一阶导数的变化控制律结构简单,通过调节控制律的相关参数,确保控制器具有较好的快速性和收敛性.

最终,为了检验本文提出的李雅普诺夫函数非线性控制器(Lyapunov function nonlinear controller,LFNC)的性能,进行了数值仿真实验,另外选取了奇异避免的反步控制器进行比较,实验结果表明本文提出的控制器(singularity avoidance back-stepping controller,SABSC)具有较好的控制性能.

2 数学模型

2.1 动力学模型

本文使用的航天器姿态动力学方程[7]如下所示:

2.2 运动学模型

2.3 一体化模型

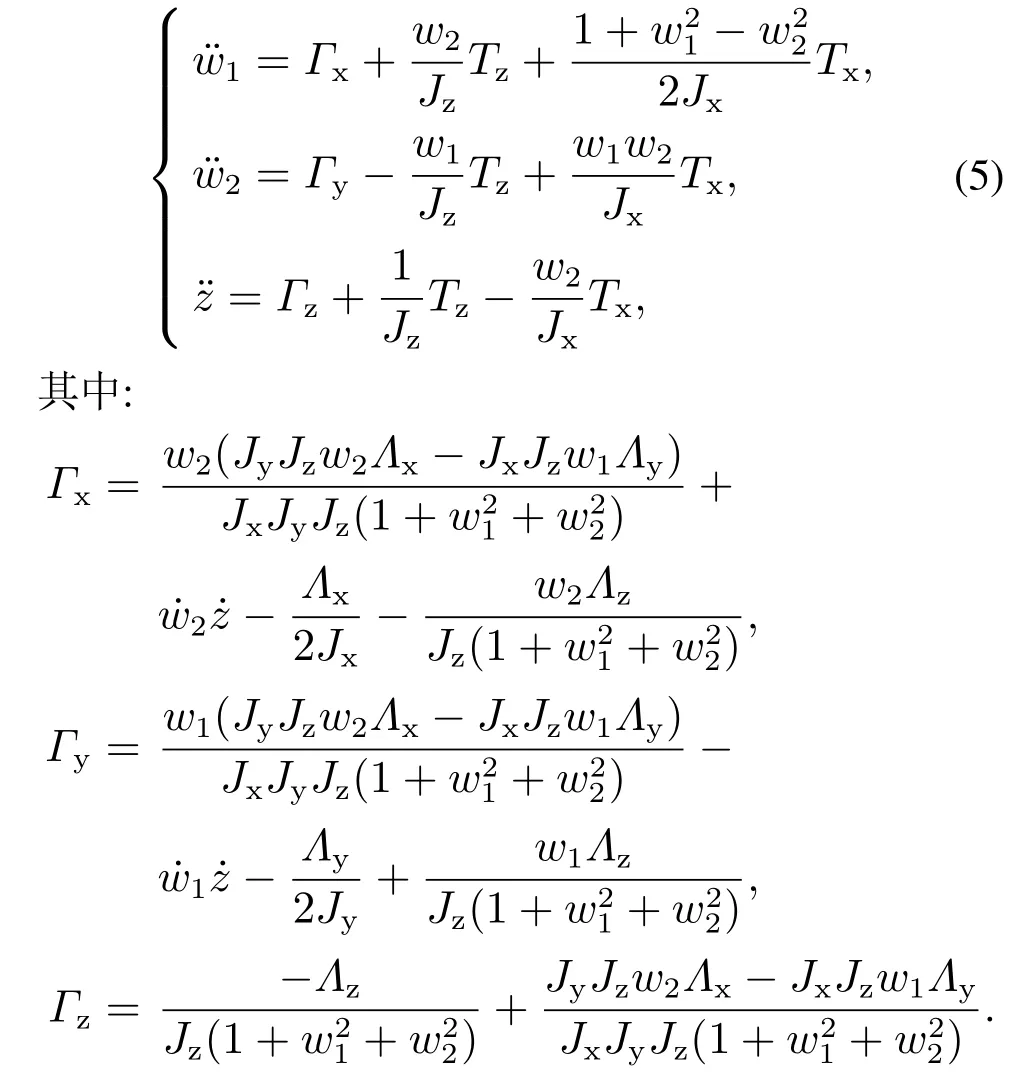
3 控制器设计

在给出的驱动轴控制力矩Tx和Tz耦合等式的基础上,通过联合解算两个耦合等式,推导得到控制力矩Tx和Tz的函数表达式,完成李雅普诺夫函数非线性控制器的设计.

3.1 Tx,Tz耦合等式设计

为了便于得到驱动轴控制力矩Tx和Tz的耦合等式,本文以w1为变量,构造的李雅普诺夫函数如下所示:

3.2 Tx,Tz设计

注3由式(20)推导得到驱动轴控制力矩Tx和Tz的函数表达式,即本文提出的李雅普诺夫函数非线性控制器,完成欠驱动航天器姿态系统的稳定控制.

此外,根据式(8)和式(21)可得

4 仿真研究

为了检验本文提出的李雅普诺夫函数非线性控制器(LFNC)的性能,另外选取了奇异避免的反步控制器(SABSC)进行比较,将LFNC,SABSC 分别与欠驱动航天控制器的运动学和动力学模型组成闭环系统进行数值仿真分析.其中航天器硬件结构参数在表1中给出.LFNC的主要控制参数在表2中列出.在LFNC的作用下,假定航天器的初始姿态角速度均为零,初始参数分别为(w1(0),w2(0),z(0))=(-0.8,0.2,0.8)rad,w1d=zd=0 rad,航天器姿态系统输出的角速度曲线等在图1中给出.

表1 航天器硬件结构参数值Table 1 Hardware structure parameter values of spacecraft

表2 LFNC参数值Table 1 Parameters of LFNC

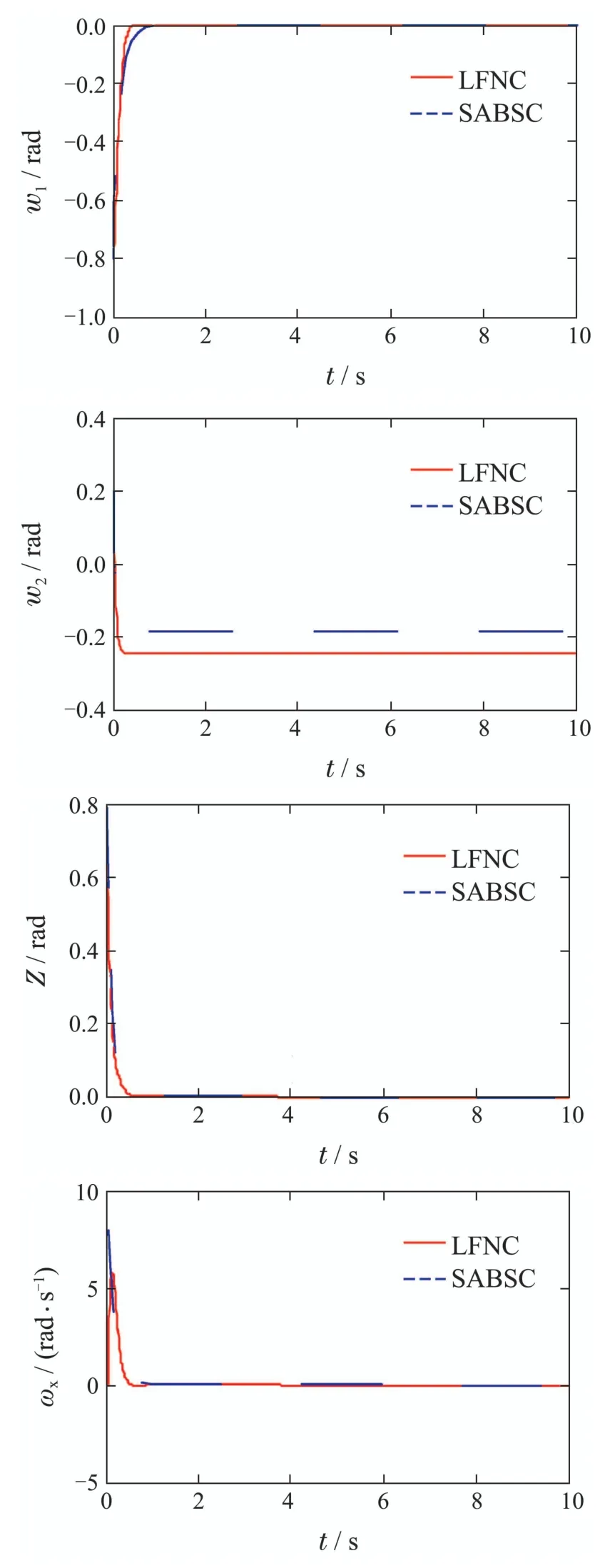
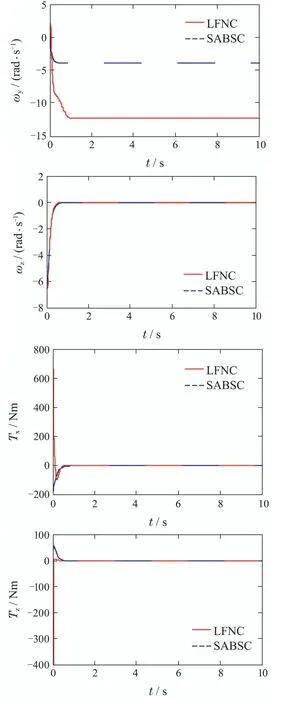
图1 w1(0)=-0.8 rad时航天器姿态系统参数的变化曲线Fig.1 Curves of parameters of spacecraft attitude system whenw1(0)=-0.8 rad

由图1可知,与SABSC相比,在LFNC的作用下,欠驱动航天器的参数w1,z,ωx,ωz在较短的时间内收敛到稳定状态,表明本文提出的控制器具有较好的快速性和收敛性,其中驱动轴的姿态参数w1,z,ωx,ωz收敛到零,欠驱动轴的姿态参数w2,ωy在三通道之间耦合控制力的作用下分别收敛到某个常值状态.

5 结论

本文主要研究了欠驱动航天器姿态系统的稳定控制问题,根据航天器姿态系统的动力学模型和利用(w,z)参数表述的运动学模型,变化得到一体化模型,本文提出了李雅普诺夫函数非线性控制器LFNC,当Ty失效时,用于完成航天器姿态系统的稳定控制.由数值仿真的实验结果可知,w1,w2,z,ωx,ωy,ωz都在较短的时间内收敛到稳定状态,表明本文给出的LFNC具有较好的快速性和收敛性.